车内噪声主动控制算法研究

李雅榕，郭 辉，王岩松，张 亮，刘宁宁

(上海工程技术大学 汽车工程学院，上海 201620)

已有被动降噪技术成功降低了车内高频噪声，对低频噪声控制效果不佳。而主动噪声控制（ANC）技术[1-4]能有效控制低频噪声，具有良好的应用前景。

目前，主动噪声控制技术最核心的部分就是对自适应算法的研究。由Widrow和Hoff在1959年提出的LMS算法，因其容易实现而很快得到了广泛应用，成为自适应滤波的标准算法。然而LMS算法存在无法同时兼顾收敛速度和稳态误差固有缺陷[5]，在工程实际中，由于次级路径的存在，其已不能保证ANC系统的稳定性。对此，Morgan[6]提出了解决方案，即在LMS算法权重更新之前放置一个与次级路径脉冲响应相同的滤波器，实现了所谓的滤波型LMS（FxLMS）算法。1981年，Burgess[7]将FxLMS算法应用于ANC系统。

结构简单、计算复杂度低的FxLMS算法[8-10]广泛应用于主动噪声控制领域，国内外学者在FxLMS算法用于ANC中的研究中取得了一定成果。Kuo等[11]发现时域FxLMS（TD-FxLMS）算法对稳态和非稳态噪声控制的鲁棒性都较好，但因为其收敛速率由参考信号的自相关矩阵特征值确定，当特征值分布范围大时收敛速度就慢。Kosaka等人[12]和Kuo等人分别对频域FxLMS（FD-FxLMS）算法进行了研究，发现FD-FxLMS算法在计算复杂度和收敛速率上有优势，但是并不适用于非稳态噪声。为了克服非稳态噪声下收敛速度慢的问题，Huang等提出了一种可变步长的FxLMS（VSS-FxLMS）算法[13]。针对实际系统中由于参考输入信号会混入与其不相关的干扰信号，束建华等人[14]利用跟踪微分滤波器和非线性变换函数分别对参考输入信号和反馈误差信号进行处理，同时，以滤波器更新向量的差值最小为优化条件推导出改进的FxLMS算法，结果证明改进后的算法在存在噪声干扰的情况下体现出更好的稳定性。Chen等人提出了频谱重塑算法，以提高实际ANC应用的收敛速度和稳定性[15]。Tang等人[16]不再拘泥于单独的时域或频域，提出了基于短时傅里叶变换（STFT）的时频域FxLMS算法，通过仿真试验证明了该算法适用于非稳态噪声，计算复杂度和收敛速度都优于TD-FxLMS和FD-FxLMS算法。然而，短时傅里叶变换存在固定分辨率问题，Qiu等人[17]应用离散小波变换的自适应算法，弥补了短时傅里叶变换的固定分辨率的缺陷。

然而，Qiu等人使用的Haar小波消失矩仅为1，对信号局部正则性的度量较差。而且，Haar小波在时域上是不连续的，作为小波基的性能不佳。因此，本文在此基础上选择正则性较好和近似对称[18]的symlet小波函数进行离散小波变换，同时，根据重构信号的能力和识别信号特征准确度的能力[19]，选择symlet小波函数族中的sym6小波与FxLMS算法结合，形成DWT-FxLMS主动控制算法。建立基于DWT-FxLMS算法的ANC系统模型，通过计算机仿真将采集的车内噪声用DWT-FxLMS算法进行处理，并与TD-FxLMS算法、FD-FxLMS算法对所采噪声的控制效果进行比较分析。

1 算法原理

1.1 FxLMS算法

在LMS算法的基础上，FxLMS算法考虑了扬声器和误差麦克风之间的次级路径。为了补偿次级路径对ANC系统的影响，在LMS算法的参考信号与滤波器之间放置估计的次级路径。由此，基于FxLMS算法的噪声主动控制原理如图1所示。

图1 FxLMS算法对噪声进行主动控制的框图

其中，自适应滤波器的输出为

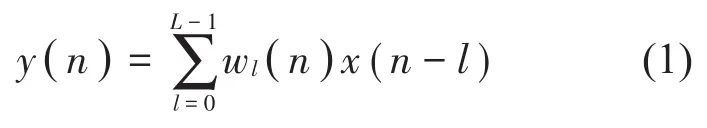
式中：x(n)是输入信号，w(n)是自适应滤波器的权系数，L是滤波器的阶数。

参考信号经过估计的次级路径，形成新的输入信号x'(n)，其表达式为

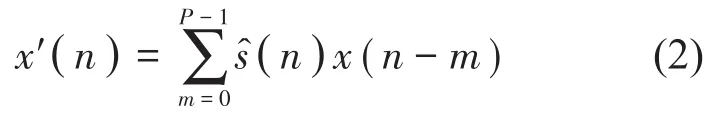
自适应滤波器权系数的更新表达式为

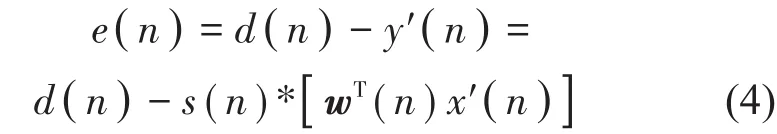
式中：d(n)是期望的噪声信号。

1.2 离散小波变换

对于离散小波变换的离散函数Uf(a,b)，将尺度因子a和偏移因子b设置为a=a0j，b=a0jnb0（j,n∈Ζ,a0＞1,b0＞0），为了使小波变换与待分析信号的非平稳性相适应，可以用二进制动态网格使小波函数有变焦功能，即当a0=2,b0=1时，每个网格对应的尺度为2j，平移尺度为2jn，因此小波函数为

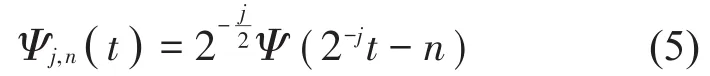
1.3 Mallat塔式算法

根据多分辨率分析理论[20]，Mallat塔式算法采用离散时间的二进制子带树结构滤波器，将连续的时间信号f(t)ϵL2(R)分解成一组近似值和不同分辨率下的细节值。分解近似和细节的特征在于具有信号f(t)所选母小波的尺度函数Φ和小波函数Ψ的内积集，表示如下

式中：Ajf和Djf是信号f(t)在分辨率第j层下的离散近似和细节，t∈Z，j=1,2,3…,J(J∈Z)，J=log2N。根据Mallat金字塔算法，高分辨率Aj+1f可以用来计算低分辨率Ajf和Djf。假设H和G是一对正交滤波器，它们的脉冲响应满足方程f和可以通过和滤波器H、G的卷积获得。h和g是重构的一对正交镜像滤波器，它们的脉冲响应和可以由H、G的脉冲响应来表示

式(10)、式(11)是一维快速小波的分解过程。而Mallat金字塔算法的重构方程为

1.4 DWT-FxLMS算法

离散小波变换将输入的时域信号进行分解，将分解后的转换域信号即子带信号进行算法处理，待算法收敛后，转换域信号再经离散小波的逆变换重构为时域信号输出。本文用离散小波变换对信号进行一层分解（j=1），图2即为所提DWT-FxLMS算法对噪声进行主动控制的框图。

(1)参考信号经小波变换后的输出

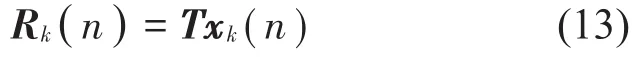
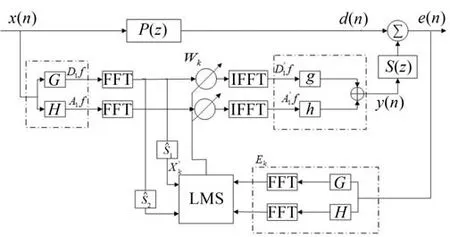
图2 DWT-FxLMS算法对噪声进行主动控制的框图

式中：Rk(n)是小波分解的数据向量，包含近似A1f与细节D1f。T是正交小波的变换矩阵。其中N为xk(n)的数据块大小。

式中：X是经估计的次级路径(n)输出的频域滤波信号。

(2)小波变换中的自适应滤波器Wk的计算

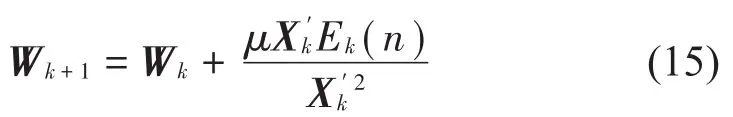
式中：μ是步长是特征值的最大值）。Ek(n)是第一层的残余误差信号。因此，当输入信号被分解到第一层时，可以得到第一层的自适应滤波更新系数

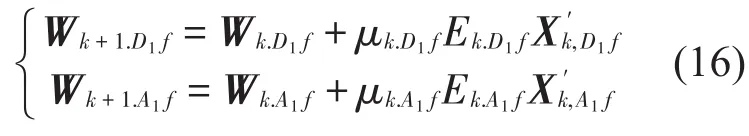
式中：Wk.D1f和Wk.A1f是第一层时滤波器的细节和近似系数。Ek.D1f和Ek.A1f是细节和近似误差信号。

(3)通过下式计算第一层的小波变换域滤波器的输出

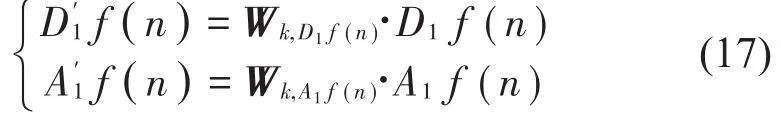
通过小波重建或小波逆变换，将小波变换域的输出变为时域输出y(n)。

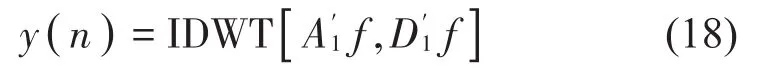
(4)残余噪声信号e(n)表示为

式中：d(n)是期望信号，y(n)是自适应滤波器输出的重构信号。

(5)残余噪声信号反馈回系统

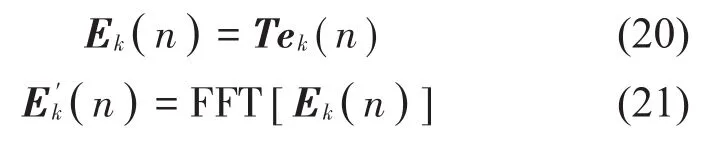
1.5 计算复杂度分析

计算复杂度分析对评估主动控制算法的有效性是很重要的，计算复杂度低将会大大减少计算时间。文献[16]中给出了TD-FxLMS算法和FD-FxLMS算法复杂度的计算，本文所提的DWT-FxLMS算法复杂度计算主要分为五步：(1)经过自适应算法输出y(n)；(2)用估计的次级路径对参考信号进行滤波；(3)滤波器权系数W(n)的更新；(4)在参考信号、滤波器权系数和残余噪声信号处进行的三次FFT变换；(5)在参考信号、滤波器权系数和残余噪声信号处进行的3次小波变换（每一次小波变换的复杂度为O(mNlogN)[21]）。根据式(13)至式(16)、式(18)、式(20)即可以针对上述5个步骤评估DWT-FxLMS算法的计算复杂度并与TD-FxLMS算法、FD-FxLMS算法的计算复杂度进行比较。其中，FD-FxLMS算法的计算复杂度需要用到以下公式。

频域自适应滤波器的输出

式中：Wk是频域自适应滤波器的系数，Xk=FFT[xk(i)]。

自适应滤波器权系数的更新

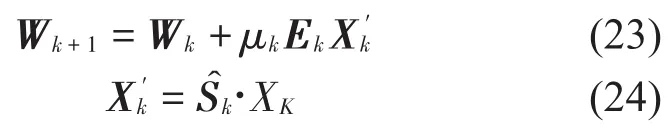
表1中总结了3种算法所需的计算复杂度，F为输出的样本数；为块数；此处的N为采样数；L为自适应滤波器W(z)的长度；P为估计的次级路径的长度；TM(×)和TA(+)为总乘法数和总加法数。为了定量比较3种算法的复杂度，表2中给出了每个算法总操作量的示例。

从表2中可以看出，DWT-FxLMS算法的计算复杂度要高于FD-FxLMS算法，但远低于TD-FxLMS算法的复杂度。

2 仿真结果分析

通过计算机仿真来比较TD-FxLMS算法、FDFxLMS算法和DWT-FxLMS算法在消除稳态和非稳态噪声上的性能。其中稳态噪声源为汽车在匀速工况下的车内噪声，非稳态噪声源为汽车在加速工况下的车内噪声。

2.1 初级、次级路径的准备

用两个低通滤波器来模拟初级路径和次级路径，该初级路径和次级路径即为所建主动控制系统的真实初级、次级路径，其时域和频域上的特征如图3所示。

2.2 估计次级路径的离线模型

本文使用离线DWT-FxLMS算法来设计估计的次级路径。首先，为提高重构信号的能力和识别信号特征准确度的能力，将离散小波的小波基定为sym6小波,并且将输入信号分解为两个子带信号；其次，设定离线DWT-FxLMS算法的各个参数，包括信号长度为16 384和估计的次级路径滤波器长度为512；再次，当算法收敛后，可以在两个子带上分别得到估计次级路径的细节响应系数D1f和近似响应系数A1f，如图4所示。

表1 3种主动控制算法的计算复杂度

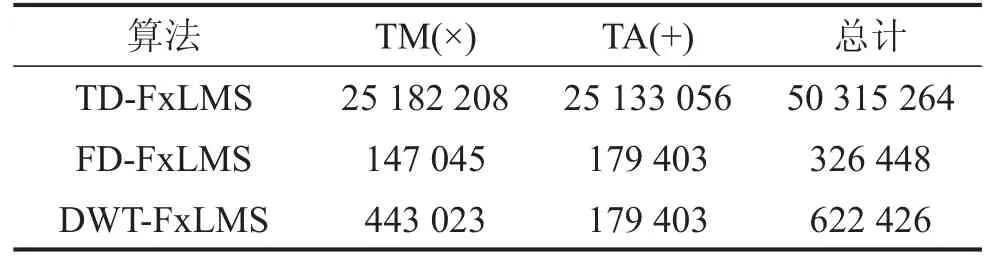
表2 3种主动控制算法复杂度的定量比较

最后，用离散小波的逆变换将近似系数和细节系数进行重构，得到最终重构后的估计次级路径的响应系数。图5为真实次级路径响应与估计次级路径响应的对比，可以看出估计次级路径的响应与真实次级路径的响应几乎完全重叠，因此次级路径的估计很准确。

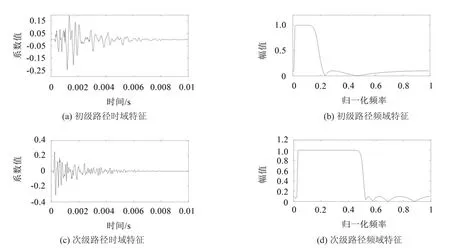
图3 初级路径和次级路径的时、频域特征

图4 用DWT-FxLMS算法得到的两子带的细节和近似系数

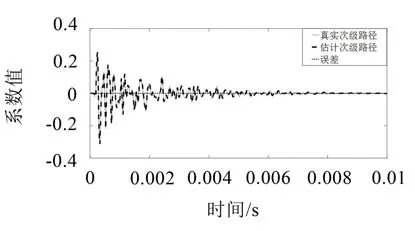
图5 次级路径响应与估计次级路径响应的比较

2.3 稳态噪声

图6为稳态噪声信号及其经DWT-FxLMS算法、FD-FxLMS算法和TD-FxLMS算法处理后的比较图。从图6中可以看出，3种算法在经过一定的迭代之后，残余噪声信号几乎都收敛为0，即3种算法都能有效地消除稳态噪声。

虽然TD-FxLMS算法、DWT-FxLMS算法和FDFxLMS算法都能有效地消除噪声，但是三者的收敛速度是有差别的。为了检验各算法的收敛速度[22]，通常使用归一化均方误差（NMSE）与迭代次数的关系图来表示。

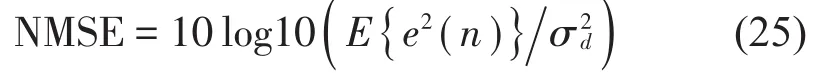
从图7中可以得知，相同的迭代次数下，FDFxLMS和DWT-FxLMS算法的对应曲线在下降段的陡斜程度相近，即两者的收敛速度相差不大。

而TD-FxLMS算法处理稳态噪声的收敛速度相对于前两种算法较慢。

2.4 非稳态噪声

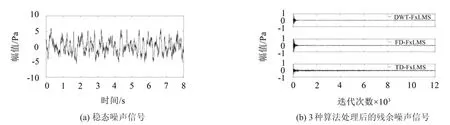
图6 稳态噪声信号及其经3种算法处理后的比较图

图8为非稳态噪声信号经DWT-FxLMS算法、FD-FxLMS算法和TD-FxLMS算法处理后的比较图。从图中可以看出，DWT-FxLMS算法经900次迭代后残余噪声信号基本为0，TD-FxLMS算法则要经近4 000次迭代后残余噪声信号才几乎为0，因此通过仿真结果证实了DWT-FxLMS算法的计算复杂度要低于TD-FxLMS算法。在处理非稳态噪声上TDFxLMS算法及DWT-FxLMS算法均能有效地消除噪声，而噪声信号经FD-FxLMS算法处理后的残余噪声的幅值一直处于波动状态，收敛效果很差，因此并不能有效消除非稳态噪声。

TD-FxLMS和DWT-FxLMS算法都能有效消除非稳态噪声，且DWT-FxLMS算法的复杂度低于TD-FxLMS算法。为了凸显DWT-FxLMS算法的优势，可以进一步比较它们的收敛速度。

图7 3种算法处理稳态噪声时收敛速度的比较

图8 非稳态噪声信号及其经3种算法处理后的比较图

从图9中可以看出，在相同的迭代次数下，DWT-FxLMS算法对应的曲线最陡，下降速度最快。即DWT-FxLMS算法的收敛速度快于TD-FxLMS算法。然而，FD-FxLMS算法因为不能有效消除非稳态噪声，所以它的收敛效果很差。

图9 3种算法处理非稳态噪声时收敛速度的比较

3 结语

本文针对车内噪声的主动控制，提出了以sym6为小波基的DWT-FxLMS主动控制算法，采用计算机仿真的方法研究了该算法的特性，得出以下结论：

（1）DWT-FxLMS算法在计算复杂度上优于TD-FxLMS算法，在消除稳态和非稳态噪声的收敛速度上也比TD-FxLMS算法更快。

（2）计算机仿真证明了DWT-FxLMS算法在消除稳态和非稳态噪声上都很有效，而FD-FxLMS算法不能有效消除非稳态噪声。

上述结论初步揭示了DWT-FxLMS算法在消除车内稳态和非稳态噪声上的优良特性，为汽车ANC技术的发展提供了一定的理论指导，同时在实际工程应用方面也有一定的参考价值。