水泥砂浆界面处纳米压痕的近场动力学模拟

赵晶晶,郭文敏，卢广达,章 青

(1.安徽工业大学建筑工程学院，安徽马鞍山243032；2.邵阳学院机械与能源工程学院，湖南邵阳422000；3.同济大学土木工程系，上海200000；4.河海大学工程力学系，江苏南京211100)

研究水泥砂浆界面过渡区(ITZ)的主要目的是探索这一区域对于水泥基材料的整体工程力学性能的影响程度，以及是否可以通过提高界面过渡区的性能来提高整个材料的力学性能[1]。目前，一些学者认为ITZ是水泥浆体和骨料连接较薄弱的区域，因此界面过渡区对于水泥基复合材料的整体性能起到重要的作用[2-4]；但Diamond等[5]认为目前并没有直接的证据能够证明界面过渡区对混凝土的力学性能会造成重大的不良影响。缺乏确凿依据的主要原因是基于界面过渡区(ITZ)的实验方法的准确性较低且实验方案本身存在偏差[6]。随着实验技术的发展，目前研究者普遍认为界面过渡区对混凝土力学性能的影响主要体现在对强度、断裂力学以及弹性模量性能方面的影响。

水化硅酸钙(C-S-H)是水泥浆体中决定硬化水泥浆体物理结构和性能的主要成分[7-8]，在对水化硅酸钙的研究中，Jennings[9]将C-S-H分为低密度C-S-H(LD C-S-H)和高密度C-S-H(HD C-S-H)两类。Jennings[10]和Tennis等[11]提出的C-S-H数值模型由5 nm直径的分散颗粒组成。本文在模拟中将水泥砂浆界面处浆体部分视为高密度C-S-H凝胶球形颗粒，对应堆积体积分数φ=0.74，通过六方密堆积HCP(hexagonal close packing)方式布置球形颗粒的C-S-H。由于砂子主要成分是二氧化硅，为了方便模拟，砂子部分由5 nm直径的分散颗粒组成。在纳米压痕模拟中，通过给出弹性模量的数值，模拟得到位移分布图、能量分布图以及作用力与位移关系的曲线图，从纳米尺度上分析界面过渡区力学性能的变化。

1 模拟方法和过程

近场动力学通过“键”的理论建立空间积分方程，突破了传统力学在处理不连续问题时的瓶颈，且该方法跳出了分子动力学方法的尺度界限，不是仅从原子尺度来解决问题，从而大大减少了计算量，并能很好地处理多尺度问题。近场动力学方法还能与分子动力学方法中的长程作用力很好地结合，主要原因是这两种方法均基于空间一定距离内物质点的作用力构建模型，而非传统力学中的物质点相互接触而产生的作用力[12]。为了研究水泥浆体与砂子交界处的力学性能，本文将近场动力学方法中的本构力函数和长程范德华力结合以构建了水泥砂浆界面处不同组分之间的作用力函数，采用Fortran语言编写程序进行模拟，并用Ensight软件进行后处理。

1.1 作用力函数

1.1.1 浆体之间作用力函数

水泥净浆的作用力函数主要分为2大部分：各向同性微观线弹性材料的PD(peridynamics，近场动力学)本构力函数、作为黏聚力部分的短程静电荷力函数和长程范德华力函数。

当0＜y＜1.1d时，根据文献[13]中提出的PD本构力函数式(1)

其中：y=|ξ+η|为变形后物质点间新的长度，ξ=x′-x为相对位置，η=u′-u为相对位移；，为弹性模量，ν为泊松比，颗粒直径d=5 nm[14]，近场范围取δ=3d=15 nm。式(1)中伸长率s计算如式(2)

并且s＜s0(t,η,ξ)，伸长率s一旦超过临界伸长率s0，相互作用力则为零，临界伸长率公式如下：

式中：s00为0.000 5；αs为0.25。

当d＜y＜1.02d时，假设短程拉力f2=-1.5 nN，短程拉力是可调节的参数，根据文献[15-16]其在1 nN左右比较合理。

当1.02d≤y＜1.1d，假设长程范德华力为主要作用力[17]，其计算公式如式(5)。

式中：a=(y-d)/d；Hamaker’s常数A=10-20J，文献[18]中指出水泥净浆中Hamaker’s常数的取值是介于云母和二氧化硅之间的一个近似值。

当y≥1.1df4=0。

1.1.2 砂子之间以及砂子与浆体之间作用力函数

由于砂子之间不存在粘聚力，所以不需要再加入短程静电荷力和长程范德华力，因此其相互之间作用力仅为PD作用力函数。在考虑砂子与浆体之间的作用力时同样忽略凝聚力，其作用力函数与砂子之间的作用力函数可具有类似的形式。

根据silling提出的均匀各向同性的弹脆性材料的PD本构力函数如下所示

式中μ是标量函数，表示物质点间破坏的状态，表达式如式(8)。

1.2 纳米压痕过程的模拟

纳米压痕模拟能够获得材料的力学性能如弹性模量和硬度，根据压痕过程所得荷载-深度曲线，计算需要的参数值。模拟中，压头作用力的计算公式如式(9)

式中：ra为压头中心到颗粒中心的距离；Nc是与压头接触的所有球形颗粒的数目；Eind为压头弹性模量；β=R+d/2，其中的R为压头的半径。Pind为压头作用力，当达到最大荷载时产生最大位移hmax。卸载曲线的顶部斜率，S为弹性接触韧度。压痕模量Er计算如式(10)

式中：Ac为最大荷载时压头与材料的接触投影面积。材料的弹性模量E可由式(11)计算

式中Pmax为下压过程中压头最大作用力。

1.3 物质点能量的描述

若在近场范围内某一物质点x′经过任意闭合回路Γ，对另一物质点x所做的功为零，即

则这一材料可以通过微弹性PD模型来进行描述，此时存在一个可微的标量函数ω(η,ξ)，使得

其中：点对势函数ω(η,ξ)仅与参考构型中物质点对变形后的距离|η+ξ|有关，类似于传统分子动力学中的势函数，表示发生相对位移η时，参考构型中物质点间“键”中存储的能量密度，用于描述近场范围δ内物质点间相互作用力的强弱。再由式(15)

可得，在小变形情况下，单一物质点间的势能函数的表达式为

式中：D(ξ)为式(14)积分后变量，通过以上计算，对近场域U进行积分，即可得到任一物质点x的点对势能函数Wu，即

将近场范围内所有与物质点x相关的物质点间产生的能量进行累加，则得到微弹性变形能密度，与传统宏观应变能密度相对应。对微弹性变形能密度积分得到系统的微弹性变形能Φu：

因此

式中：b为外力密度；Tu为系统动能；R为近场范围积分域。由式(21)可以看出，在没有能量损耗的情况下，外力所做的功等于微弹性变形能以及动能之和。对于准静态或静力问题，式(21)中的系统动能可基本忽略，即Tu=0。

1.4 模型建立

模型尺寸设定为100 nm×100 nm×60 nm。模拟中采用的是半球形压头，压头半径为15 nm，在砂子和水泥浆体界面中央垂直下压，最大下压深度为15 nm。球形颗粒排列采用HCP方式，堆积密度为0.74[14]。图1为模型示意图，其中模型左半块为砂子，右半块为水泥浆体，球形颗粒直径均为5 nm。压头下压速度为1 nm/s，恒载1 s后，以1 nm/s速度卸载。水泥颗粒密度为2.6 g/cm3[19]，砂子密度为1.4 g/cm3，时间步长为10-5s。Jennings[20]和Constantinides等[21]指出球形颗粒状水化硅酸钙的弹性模量Ea的范围在48～65 GPa。在PD函数中，式(1)中的c系数分别取Ea的最小值为48 GPa最大值为65 GPa，以及超出范围的特殊值70 GPa。砂子的弹性模量Eb根据实验内容取为110 GPa[22]。砂子与水泥界面处作用力函数中输入的弹性模量数值为两者之和的平均值。阻尼系数c为104，临界伸长率为1010。模拟过程中采用Velocity-Verlet算法[23]。

图1 水泥砂浆界面模型示意图Fig.1 Model of cement mortar interface

2 模拟结果与分析

2.1 位移

图2给出了压头下压过程中界面处材料的变形情况。图中左半块代表水泥浆体，右半块部分代表砂子。模拟开始以后，随着压头荷载的逐渐增大，受压部分的位移也逐渐增大，纳米压痕最大深度为15 nm，变形基本一致。从图中可以看出，整个下压过程中，系统保持稳定。并由此过程可以给出压头作用力，进而通过荷载-位移曲线计算弹性模量和硬度值。

图2 纳米压痕模拟过程图Fig.2 Process of nanoindentation simulation

从图3可以看出，随着压头下压深度的逐渐加大，材料与压头接触面越来越大，最先接触部分产生的z方向位移最大。设定压头下压最大深度为15 nm，从图3(d)可以看出，与压头顶端接触部分材料的最大位移和压头下压深度基本保持一致。并且在最大位移产生时，整个水泥砂浆均有一定位移产生，接触面形成一个有弧度的微曲面。

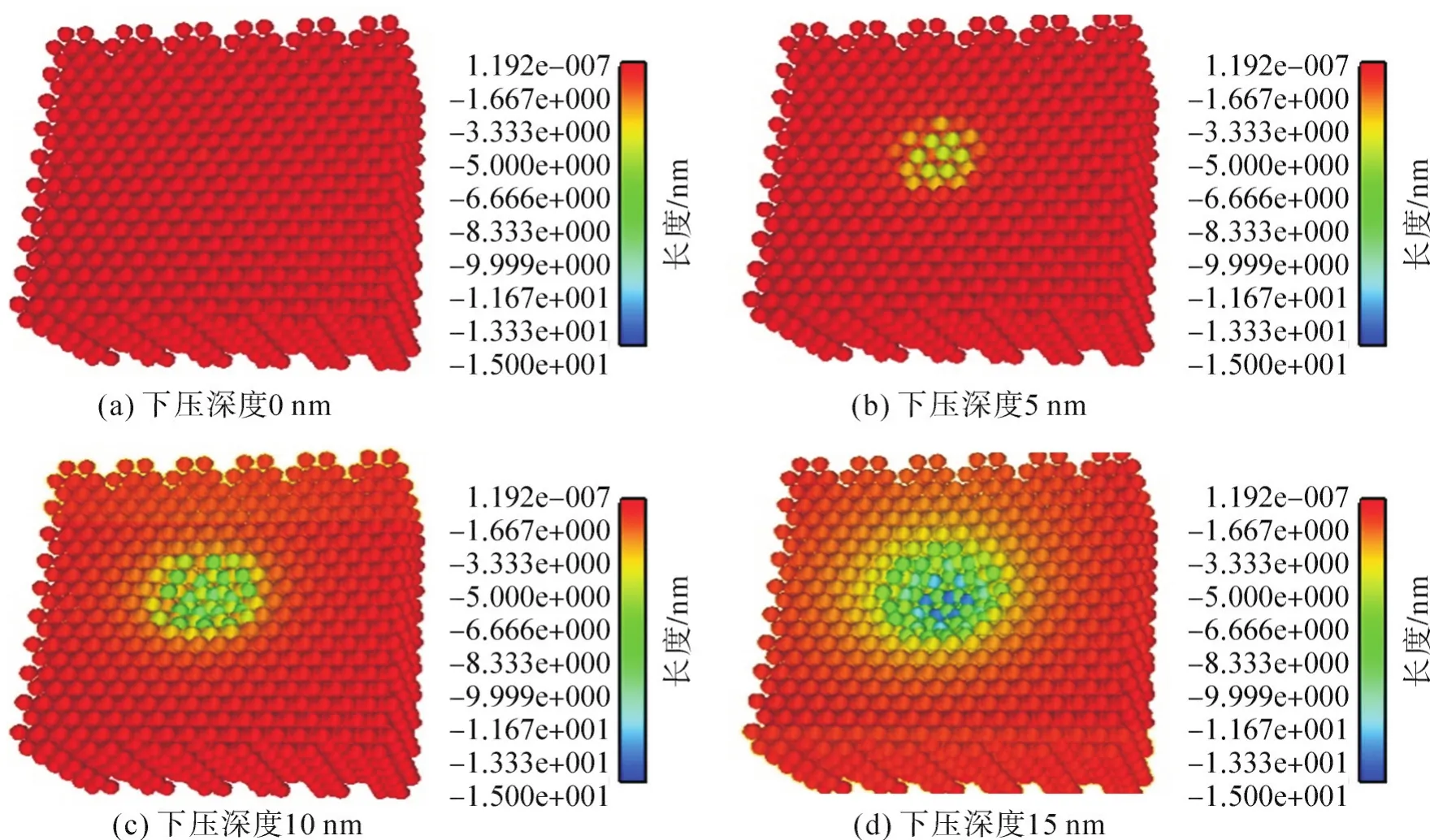
图3 纳米压痕模块位移云图Fig.3 Displacement graph of nanoindentation module

2.2 能量

当Ea=65 GPa时，能量的分布与Ea=70 GPa时基本相同，但Ea=70 GPa时，位移作用力曲线的震荡幅度更加稳定。图4，5分别给出不同下压深度，Ea取值为70，48 GPa时对应水泥界面剖面和砂子界面剖面处的能量分布图。

图4 Ea=70 GPa时界面处水泥剖面与砂子剖面的能量分布云图Fig.4 Graph of the energy distribution when theEa=70 GPa

从图4中可以看出，压头下压位移为15 nm时，砂子部分的能量分布图中出现了深色的区域，而水泥浆体部分最大值则呈现淡色区域部分。对比下压位移分别为5，10 nm的能量分布图可以看出砂子部分能量分布的最大值大于水泥部分，并且砂子部分能量分布范围更大，砂子部分聚集了更多的能量。

对比图4，5可以看出，能量分布的数值区域基本相同，其中水泥浆体部分能量最大值集中在7.133×107nN×nm附近，砂子部分能量最大值集中在10.07×107nN×nm附近。模块中砂子部分聚集了更多的能量，并且其受影响范围更大。表明在相同变形条件下，弹性模量数值较大的部分在能量的聚集和传递上承担较多。分别对比图4，5中水泥浆体部分，在压头下压位移为15 nm时，Ea=70 GPa的能量云图比Ea=48 GPa的能量云图分布更广，且颜色上更趋于深色部分，即数值更——表明弹性模量较大的模块聚集了更多的能量。由于砂子部分采用的弹性模量数值均为110 GPa，故图4，5中砂子部分能量分布基本相同。

2.3 作用力-位移曲线

砂子与水化硅酸钙之间的作用力公式中的弹性模量数值，取砂子和水化硅酸钙的弹性模量数值之和的均值。通过模拟纳米压痕过程计算得到压头作用力-位移曲线如图6。

图5 Ea=48 GPa时界面处水泥剖面与砂子剖面处的能量分布云图Fig.5 Graph of the energy distribution versus theEa=48 GPa

当Ea=48，65 GPa时，压头z轴方向最大作用力均在5.0～6.0 μN 之间；当Ea=70 GPa时，压头z轴方向最大作用力为6.1 μN。从图中可以看出压头作用力与深度曲线之间的关系为递增，在曲线上升过程中，有起伏振荡。这一现象产生的原因是颗粒的分布采用的是HCP方式，在压头下压过程中，当压头作用力积累到一定程度时，会导致其下压方向产生整体的滑移，因此抵抗下压的作用力减少，形成压头作用力的起伏振荡。其中，Ea=48 GPa振荡幅度较大，比较不稳定；Ea=70 GPa时振荡幅度较小，整体平稳上升。原因主要在于界面处两种弹性模量数值相差较大，从而引起压头作用力震荡幅度较大。当压头达到最大作用力后，按线性速度回撤，根据式(10)和(12)计算得到相应的压痕模量和硬度值，如表1。

图6 Ea=48,65,70 GPa时压头作用力-位移(P--h)曲线Fig.6 P-h curves of head whenEa=48,65,70 GPa

从表1中可以看出，当取不同Ea值时，硬度值变化幅度基本相近。当Ea＝48 GPa时压痕模量数值变化较大，主要原因是砂子和水泥弹性模量数值取值差异较大，砂子部分对整体界面处弹性模量产生了较大的影响。通过实验方法也可以测得较高砂率的水泥砂浆的弹性模量在其他条件相同的情况下大于砂率小的水泥砂浆的弹性模量。表中所示压痕模量和硬度值均大于水化硅酸钙的压痕模量和硬度值，而在实际情况中，界面往往是薄弱区域，弹性模量和硬度值应小于水泥净浆对应的量。导致目前这种现象的主要原因是模型并未考虑界面处的孔隙率和水化度，如何在计算模型中考虑这些因素的影响，进行更加精确的模拟计算，还需要进行系统和深入的研究。

表1 不同Ea值时界面处压痕模量Er和硬度值H，GpaTab.1 Indentation Modulus and hardness of the interface with different values ofEa,GPa

3 结 论

建立了水泥砂浆界面过渡区的计算模型。模型中，将纳米尺度的水泥浆体和砂子均视为球形分散颗粒的集合，分别构建了浆体和砂子的作用力函数以及它们之间的作用力函数，对界面区纳米压痕的数值模拟研究，得到了水泥砂浆界面处力学性能的变化特征。结果表明：水泥砂浆界面处水泥部分和砂浆部分的能量分布有明显区别，砂子部分的能量数值大于水泥部分。界面过渡区的力学性能与基体材料的性能密切相关，并呈现出高度的非均匀性，也验证了水泥砂浆界面过渡区力学性能相对薄弱的事实。采用近场动力学和分子动力学相结合的方法为水泥基材料力学性能的计算模拟提供了一个新的途径，计算模型还可以继续丰富发展。比如考虑界面过渡区的客观存在的未水化的水泥颗粒和毛细孔隙，同时还可以考虑各种环境因素如温度，湿度等的影响。以更好地分析水泥材料微观尺度的力学性能以及微观结构对水泥基材料宏观尺度性能的影响。