自动换刀机械手控制系统建模

张继红

（四川职业技术学院，四川 遂宁 629000）

1 引言

自动换刀机械手的控制是整个系统的关键，要按照预定的轨迹进行运动，并保持末端的位姿准确性，就要控制好运动的坐标，速度及加速度。同时为了保证换刀过程中卸刀、入库、取刀、装夹的可靠要求，就要控制机械手的手抓有合理的抓举力。控制系统的动态技术指标决定了控制性能的质量。建立机械手控制系统的数学模型并进行计算机数字仿真是设计控制系统有效的手段。它能方便地提出改进现有系统的措施，能在系统建立之前对其动态性能进行预测。按机械手控制系统物理量之间的动力学关系，建立描述该系统数学模型，并进行计算机仿真。

2 多关节机械手控制特点

机器人控制系统是一个多轴协调运动控制要求的系统，换刀机械手从结构上由连杆通过关节串联的空间开链结构，实现末端的运动和动力控制需要各关节的协调运作。如图1的多关节机械手[1]具有多轴多连杆多关节构成的多自由度体系。它的控制比传统的机械系统的控制复杂得多。因为机械手控制系统是与运动学，动力学相关的，并且有耦合的，非线性的，多变量的多输入输出控制系统。

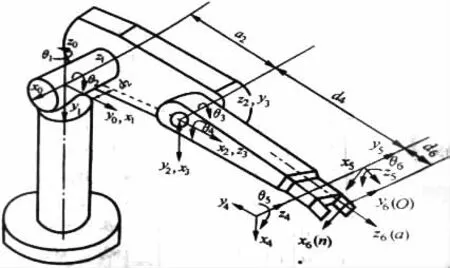
图1 多关节机械手

换刀机械手位置的控制就是使各关节实现预期的规划运动，以保证末端按规定的轨迹从起点准确运动到终点。由于是多关节耦合的非线性系统，实施严格的控制很困难，控制系统的设计复杂，所以实际设计中通常按照独立关节来处理。为了简化设计通常把换刀机械手多关节串联组成的各关节按独立线性控制系统处理。其原因在于运动的速度不高可以忽略引起的非线性，各关节的驱动电机与大传动比的减速器连接降低了负载的影响，而关节间的耦合作用也减弱了，设计的系统能满足使用要求。

3 直流伺服电机驱动的关节控制建模

3.1 机械传动系统的建模

换刀机械手是一个复杂的机电系统，其动力学模型的建立涉及到机械传动系统、电路网络、伺服控制电机元件。

多关节机械手关节是转动副，机械传动系统元件有转动惯量、阻尼器和弹簧。下面分别对转动惯量、阻尼器和弹簧建立其数学模型。

转动惯量简化模型如图2所示[2]。它由一个转动惯量的转动体构成，其转动角为θ，转动惯量为J，作用在转动体上的外力矩为M。

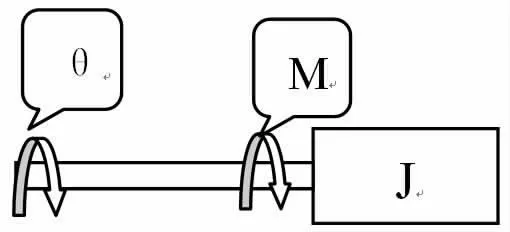
图2 转动惯量

则转动惯量的数学模型为：

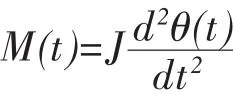
阻尼器简化模型如图3所示。它由一个阻尼系数为f的阻尼器构成，其转动角为θ1和θ2，作用的外力矩为M。

则阻尼器的数学模型为：

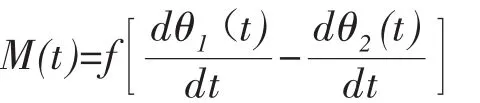
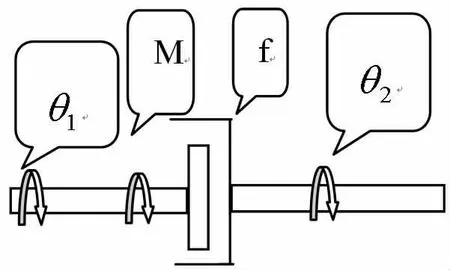
图3 阻尼器

弹簧简化模型如图4所示。它由一个弹簧刚度为K的扭转弹簧构成，其转动角为θ1和θ2，作用的外力矩为M。

则弹簧的数学模型为[3]：

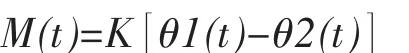
一个综合的机械转动系统包含有转动惯量、阻尼器和弹簧[4]，如扭摆系统，它由一个转动惯量为J，摆锤与空气的阻尼系数为f的阻尼器和弹簧刚度为K的扭转弹簧构成的综合的机械转动系统。

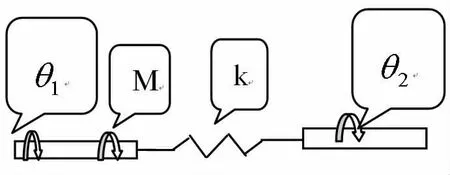
图4 弹簧

则数学模型为：经拉氏变换，整理得该系统的传递函数为;

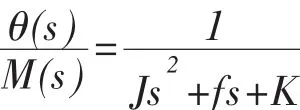
这是一个二阶系统。

3.2 电路系统的建模

换刀机械手的某一关节控制的电路系统包括电路网络、伺服控制电机。

电路R C网络如图5所示：它由一个电容和电阻构成，输入电压为ui,输出电压为uo。可用消元方法求其传递函数。

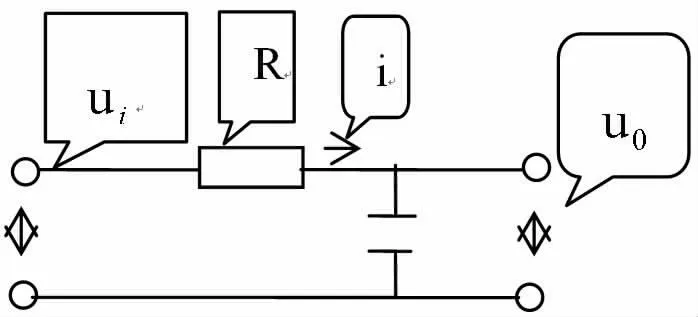
图5 RC网络

则R C网络数学模型为：

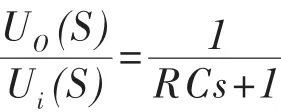
3.3 直流伺服电机驱动的关节控制建模

多关节机械手的控制涉及到末端器的位置控制，以及手抓的力度控制。有的机械手如完成喷涂作业的机械手，点焊作业的机械手只对机械手完成位置控制即可。要完成抛光作业的机械手，完成装配作业的机械手，要求手抓与工件保持一定大小的夹持力，除了完成作业自由度方向的位置控制外还要完成接触力的控制。故机械手常见的控制系统如：基于直流伺服电动机驱动的关节机械手控制，基于交流伺服电动机驱动的关节机械手控制，质量-弹簧系统的力控制，力-位混合控制等。下面以常用的基于直流伺服电动机驱动的关节机械手控制来建立其数学模型。

换刀机械手采用直流伺服电动机驱动，其简化模型如图6所示[5]。它的基本结构是由电枢直流伺服电机带动齿轮变速器，然后再驱动机械手臂运动，完成位置控制。变速器主动轮，从动轮。

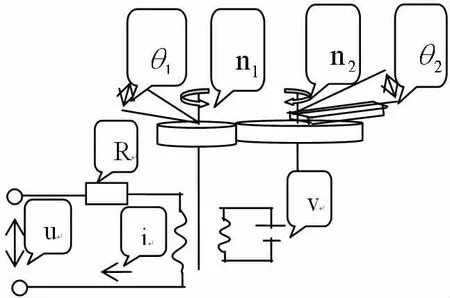
图6 直流伺服电动机驱动关节模型

下面来建立关节驱动控制系统的数学模型。该系统由机械部分、电气部分和机械电气耦合部分构成。

电动机轴转动系统的数学模型：

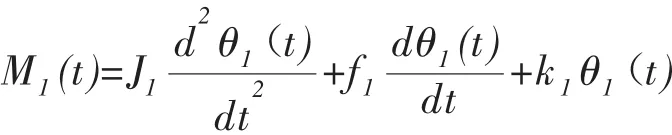
式中：M1--电机轴转矩，M2--负载轴转矩，J1--电机轴转动惯量，f1--电机轴阻尼系数，k1--电机轴弹性模量，θ1--电机轴转角。变速器传动比：

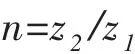
式中：n--传动比,z1--主动轮齿数，z2--从动轮齿数。

则有：M2=nM1,θ1=nθ2。

负载轴转动系统的数学模型：

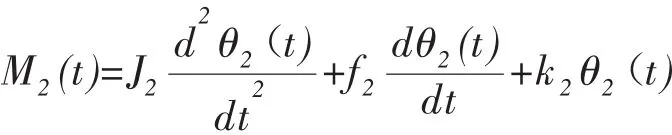
式中：M2--负载轴转矩，J2--负载轴转动惯量，f2--负载轴阻尼系数，k2--负载轴弹性模量，θ2--负载轴转角。

电枢式直流伺服电机控制系统的电路数学模型：

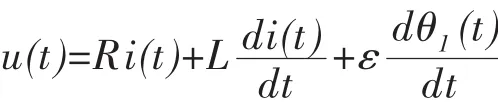
式中：u--电枢电压，R--电枢电阻，L--电枢电感，ε--反电动势常数。

耦合部分的数学模型：

式中：kt--电动机力矩常数。

由于L很小，令L=0，以电枢电压u为系统输入，负载转角为输出。

令 θ(t)=θ2（t）

消去中间变量则得机械手关节控制系统的数学模型：

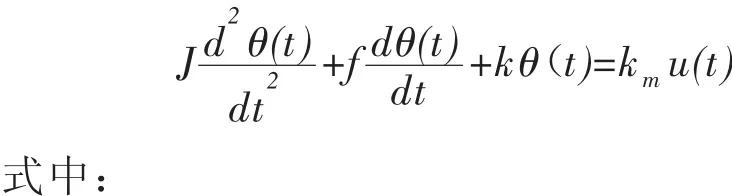
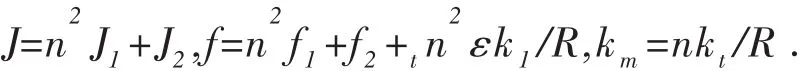
由于轴的刚性很大而忽略扭转弹簧作用，则经拉氏变换的控制系统的传递函数：

为二阶系统[6]。在系统的数学模型基础上，利用S I MU软件对控制系统进行计算机仿真计算。输入系统的结构参数，仿真出系统的动态性能指标，寻找出最好的控制设计方案。

4 结论

对自动换刀机械手控制系统进行建模，是多关节机械手动态性能分析的有效手段。但由于多关节机械手本身的非线性、相互耦合性以及多变量特点，系统设计时需应用现代控制理论分析计算，非常复杂。基于低速、负载影响小等实际特点，把多关节控制系统简化为独立的单关节控制系统，利用经典控制理论分析建立数学模型，并利用S I MU语言[7]进行仿真.得到不同输入的时间响应，选择系统的参数匹配最佳、动态特性最好的控制方案。