2.3离散型随机变量的均值与方差
——2.3.1离散型随机变量的均值
2018-02-19天津市第四中学高达溟
天津市第四中学 高达溟
教学目标:
1.知识与技能
了解离散型随机变量的均值或数学期望的意义,会根据离散型随机变量的分布列求出均值。
2.过程与方法
理解数学期望的性质和常见分布的数学期望,能熟练运用它们求相应的离散型随机变量的数学期望。
3.情感、态度与价值观
培养学生的科学态度,勇于探索和敢于创新的精神。体现数学的文化功能与人文价值。
重点难点:
教学重点:离散型随机变量的均值或数学期望的概念。
教学难点:根据离散型随机变量的分布列求出均值或数学期望。
教学过程:
一、复习旧知
1.随机变量
如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量 随机变量常用希腊字母ξ、η等表示。
2.离散型随机变量
对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量
3.分布列
设离散型随机变量X可能取得值为x1,x2,…xi,…xn。
X取每一个值xi(i=1,2,…)的概率为P(X=xi) =pi则称表

为随机变量X的概率分布,简称X的分布列
4.分布列的两个性质: ⑴Pi≥0,i=1,2,…;⑵P1+P2+…=1.
二、引入新课
根据已知随机变量的分布列,我们可以方便的得出随机变量的某些特定的概率,也就掌握了随机变量取值的统计规律。但分布列的用途远不止于此,
问题1:已知某射手射击所得环数X的分布列如下

在n次射击之前,可以根据这个分布列估计n次射击的平均环数.这就是我们今天要学习的离散型随机变量的均值或期望
问题2:如何估计该射手n次射击的平均环数?
根据射手射击所得环数X的分布列,
我们可以估计,在n次射击中,预计大约有
P(X=4)×n=0.02n次得4环;
P(X=5)×n= 0.04n次得5环;
…………
P(X= 1 0)×n= 0.22n次得10环.
故在n次射击的总环数大约为
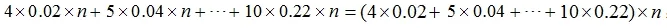
从而,预计n次射击的平均环数约为

这是一个由射手射击所得环数的分布列得到的,只与射击环数的可能取值及其相应的概率有关的常数,它反映了射手射击的平均水平.
对于任一射手,若已知其射击所得环数X的分布列,即已知各个P(X=i)(i=0,1,2,…,10),我们可以同样预计他任意n次射击的平均环数:
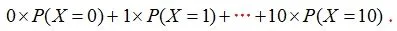
三、推进新课
1.均值或数学期望
一般地,若离散型随机变量ξ的概率分布为

均值或数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平
注意:
(1)区别X与E(X)
随机变量X是可变的,可取不同的值;
均值E(X)是不变的,它是离散型随机变量的一个特征数,由X的分布列唯一确定,它反映X了取值的平均水平。
(2)区别随机变量的均值与相应数值的算术平均数。
均值表示随机变量在随机试验中取值的平均值,它是概率意义上的平均值,不同于相应数值的算术平均数。
例1口袋中有5只球,编号为1,2,3,4,5,从中任取3球,以X表示取出球的最大号码,求E(X)。
2.均值的性质
(1)若Y=aX+b(a、b是常数),X是随机变量,则X也是随机变量,它们的分布列为
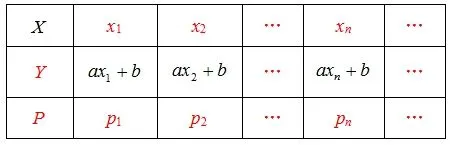
由此,我们得到了期望的一个性质:E(aX+b) =aEX+b
(2)若X1,X2,…Xn为随机变量,则
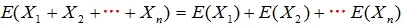
例2.袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有个n (n=1,2,3,4)。现从袋中任取一球。X表示所取球的标号。
(1)X求的分布列和均值。
(2)若Y=aX+ 4 ,E(Y)=1,求a的值。
3.几种分布的期望
例3 (2015天津)为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(I)设A为事件“选出的4人中恰有2 名种子选手,且这2名种子选手来自同一个协会”求事件A发生的概率;
(II)设X为选出的4人中种子选手的人数,求随机变量X的分布列和数学期望.
四、小结
(1)离散型随机变量均值的定义
(2)均值的性质;
(3)几种分布的期望。
