基于数轴折叠问题谈学生数学思维提升

数学核心素养是在数学学习过程中逐渐形成的具有综合性、整体性和持久性的学科素养，反映了数学本质与数学思想。在数学教学中，如果能以常态数学习题，加以变式、挖掘、拓展和延伸，学生就能更加快速、深刻地理解、内化和建构知识，提升思考、解决问题的能力。本文以一道七年级数轴折叠问题为例，在“变”中求“实”，启发学生数学思维。

一、一道常态习题引发的思考

题目：操作探究已知在纸面上有一数轴（如图1）

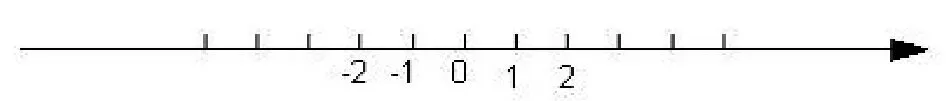
图1

操作一：

（1）折叠纸面，使数字1表示的点与-1表示的点重合，此时中心点为0，则-3表示的点与_____表示的点重合；

操作二：

（2）折叠纸面，使-1表示的点与5表示的点重合，回答以下问题：

①此时的中心点是______，则10表示的点与数_____表示的点重合；

②若数轴上A、B两点之间距离为15，(A在B的左侧)，且A、B两点经折叠后重合，求A、B两点表示的数是多少?

这是七年级第一学期期中测试中的一道解答题，看似不难，但学生的得分率并不理想。具体得分率统计如表1。

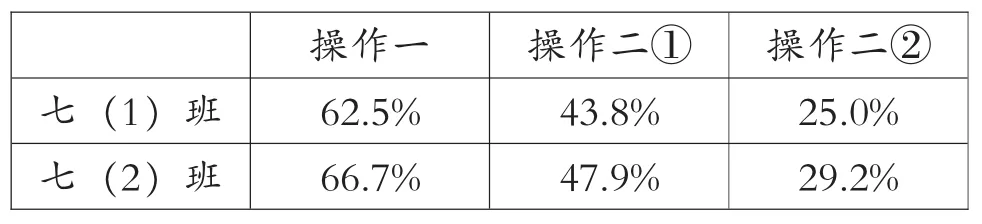
表1

注：两班学生均为48人。

对于操作一，据调查统计学生的解题依据是：①题目已经给出图形，学生可根据中心点0直观地找到-3的重合点；②部分学生想当然认为因已知-1和1重合，所以-3就和3重合。虽然得分情况尚可，但是学生分析问题的思考层面很低，没有为进一步解题做好思维铺垫。

对于操作二中的问题①，因没有理清操作一的解题思路，多数学生找不出中心点的改变，故得分率骤减；对于问题②中反向思考问题求解，学生的困难就更多了，得分人数寥寥。

面对七年级学生数轴问题探究瓶颈，如何渗透数形结合、分类讨论的数学思想，有效运用核心知识与方法解题，引发了作者反思：能否用“变式”设计，打通解题困惑。

二、以变式寻求多维张力

1.铺设问题引例，拓展思维广度，培养问题概括能力。

引例：

（1）根据图2中A、B、C三点的位置，请分别算出A到B，C的距离。并观察你所计算的距离你有什么发现？

（2）再观察数轴，求到点A的距离为4个单位长度的点表示的数是：

图2

设计意图：由浅入深，探究前引例梯度性铺设，激发学生学习积极性。在学习并掌握了数轴知识后，学生能利用数轴这个工具，直观地计算数轴上两点间的距离。但本引例的出发点不止如此，它需要学生进一步概括出数轴上计算任意两数之间距离的简化公式：“大数减去小数的方法”。引例2中已知一点和相距的距离，求出满足条件的点表示的数。这是一个逆向思维过程，需要学生结合数轴中相反数和绝对值的意义解题。若脱离数轴这个直观工具解题，则往往会出现漏解。因此本题的设计意图在于通过基础题的练习，让学生初步感受问题解决时所渗透的一些数形结合、分类讨论的思想。

2.改变问题背景，挖掘思维深度，培养求同存异能力。

操作探究：已知在纸面上有一数轴（如图3），

折叠纸面一，使数1表示的点与数-1表示的点重合，则此时数-2表示的点与数______表示的点重合；思考：a表示的点与_____表示的点重合?

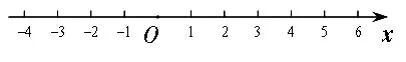
图3

设计意图：以“折叠数轴”这一动态操作，引导学生探究已知一对数重合怎样寻找中心点。为了让学生对解题思维有一个规律性的总结，追加设计思考：a表示的点与_____表示的点重合。用字母表示数，从直观到抽象启发学生归纳出当中心点为数轴原点时折叠重合的两数关系。此设计意为引导学生发散思考：当中心点发生改变时，重合的两数关系是否会改变，从而提高学生思维的深度。

3.改变折叠中点，提升思维高度，培养探索发散能力。

折叠纸面二：使数3表示的点与数-1表示的点重合，回答下列问题：

（1）数5表示的点与数______表示的点重合；

（2）思考：b表示的点与数______表示的点重合；

设计意图：更换中心点再折叠数轴，此变式解题的思维高度明显提升。解答时，学生需要归纳出：①找中心点的一般方法；②如何计算点与中心点的距离；③用字母表示数后，启发学生归纳出当中心点为任一点时折叠重合两数的一般表达式。

4.互换条件结论，改变思维效度，培养逆向思维能力

折叠纸面三：使数3表示的点与数-1表示的点重合时，若数轴上有A、B两点也重合，且A、B两点之间的距离为10（A在B的左侧），则A点表示的数为______，B点表示的数为______.

设计意图：改变已知条件，由已知中心点和重合两数的距离反向求解重合的两数。训练学生逆向思维能力，应用已知解题方法解答问题，从而提升学生思维效度。

5.由特殊到一般，改变思维密度，培养灵活概括能力。

折叠纸面四，使数3表示的点与数-1表示的点重合时，若数轴上有A、B两点也重合，此时A、B两点之间的距离为n（A在B的左侧），则A点表示的数为______，B点表示的数为______.

设计意图：变式四是变式三的进一步提升。改变已知条件中重合两数的距离为任意值，反向求解重合的两数。此题要求学生在对解法的总结反思中，将结论一般化，培养灵活概括能力。

数轴上的折叠问题涉及初步数形结合、分类讨论思想。通过层层递进的变式教学，学生从中整合了知识，落实了基础，熟练了方法，学会了学习，培养了思维，提升了能力，完成举一反三，大大提高数学素养。

学习是一个渐进过程，教学也是一种复杂艺术。教师需要不断寻找知识的结合点与方法的生长点，通过多样化的习题教学，引导学生深层次地思考数学问题，体验丰富多彩的数学活动，感受多变的数学思维之美。