数学教学中学生整体思维的提升路径探析

《义务教育数学课程标准（2011年版）》中指出，通过数学学习学生应能“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力。”20以内的进位加法是一年级上册计算教学的重点，也是多位数加法以及多位数乘法的基础，进位加法表则是学生在10以内的加法表和减法表之后第二次对计算内容的整理。在实际教学中，这部分内容的目标仅仅定位于提高学生口算的速度。如何设计活动，发挥进位加法表的价值，提升思维能力？我们教研组进行了尝试与探索。

一、经历完整的整理过程，利用生成资源引发互动，获得方法

【现状】教师呈现半成品的加法表，让孩子对之进行补充，学生很容易完成了加法表的补充任务。

【思考】学生凭借之前学习的经验能轻松完成任务，但对于整体的结构并未了解，只是停留在局部算式的关系中，如果放手给学生自己整理，他们会怎样呢？

【实践】活动：整理进位加法表

师：我们已经学习了这么多进位加法算式（口算后的卡片杂乱地放在黑板上），你们觉得如何？

生1：太乱了，要摆整齐了才好看。

师：是呀，你们会将这些算式整理一下吗？请拿出36张口算卡片，在桌子上摆放整齐，便于大家能看明白，也方便我们记住它们。（生开始摆。学生边摆边算，先摆好的学生再看同桌怎么摆的，10分钟后，只有两个孩子没有完成。有层次地展示学生的照片，学生进行点评）

师：你们觉得他摆的怎样呢？（用手机拍摄学生的作品投射到电子白板上。出示图1，生都笑了）

生2：他摆的是笑脸，还有好多算式没有用呢。

生3：他摆的算式没有规律。

师：是呀，他考虑摆出的形状，但忽略了我们要将这些算式都整理出来，还要考虑算式间的关系。

师：出示图2，这个小朋友整理的怎样呢？

生4：他摆的是有顺序的，但接的太长了，要将9加几、8加几分开来看更清楚。

师：出示图3，这个小朋友摆的呢？

图1

图2

图3

生5：他分开来摆了，但是分的太开了，要靠紧一些，看起来方便。我是竖着放的（指着图4），这是9加几，这是8加几……横着这是得数都是11的，这是得数都是12的……

生6：（有一孩子激动地站起来）老师，我摆的和她是反的。

师：（展示图5），比较一下，确实是反的，怎么是反的呢？（学生找不出理由）

图4

图5

师：看横行，你为什么将8+3放到下面呀？

生6：（学生走到黑板前指给大家看）这里是9+3，8+3就和它对齐了。

生5：8+3=11，9+2=11，我将8+3就和9+2对齐了。

师：一个是按第二个加数相同摆的，一个是按得数相同摆的，都有自己分类的标准。整理加法表时按自己分类的标准，按一定的顺序摆出来都可以。

在实际教学的整理环节，学生用了10分钟来整理加法表，他们一点没有闲着，需要找算式、找相同点，还要算一算，整理出来的加法表中隐藏的规律已经内化在他们的操作中，与发现成品加法表中的规律相比，学生经历了整理的过程，探索意识得到激发。学生的差异不仅体现在整理速度上，还体现在对算式的敏感程度、思维水平上，需要运用学生生成的资源组织交流互动。从笑脸图案到一条长龙直至加法表，让学生在分析自己的作品中逐步理解为什么这样整理，整理要注意些什么，在这个过程中学生不仅理解了算式间的联系，也获得了整理算式的方法，感悟了分类在整理中的价值。

整理，指对内容零散、层次不清的已有文字作品或者材料进行条理化、系统化的加工，让学生经历完整地探究过程，才会自觉将进位加法表建构为一个整体结构。

二、融入奇趣的游戏元素，创设对话机会促进分享，增强能力

【现状】教师引导学生观察加法表，找到规律后，比一比谁算的快。

【思考】所有的进位加法算式，学生都已经进行了训练，如果教师训练扎实，这一要求学生能轻松达到，而只是算得快的要求与视角，是否降低了教学要求？

【实践】活动：关于口算卡片的游戏

师：我们来研究这个同学摆出的加法表，你们知道他是怎么摆的吗？（拉开黑板，出示上课前用磁性口算卡片摆好的加法表）你能找到规律吗？

游戏1：报得数

师：运用你们发现的规律考考你们。我指一道，你们报得数。（尽管是随机出现，但学生算得很轻松）

游戏2：找算式

下面我们做游戏，看谁能猜出老师拿走了哪道算式？

师：天黑请闭眼。（所有学生闭上眼睛，教师拿走7+7藏在身后）天亮请睁眼。猜猜哪道算式少了，为什么？

生：7+7，因为上面是7+5、7+6，下面就是7+7

师：如果是横着看，你能发现吗？

生：因为前面是9+5、8+6，前面越来越小，就是7+7。

游戏3：男女生PK游戏（教师拿出6+7）

（1）比比谁说的相等的算式多。男女生各出一代表对接：5+8、9+4、4+9、8+5、7+6比赛不分胜负。

（2）比比谁能最快说出得数比6+7少1的算式。

女：6+6，因为6+7=13，少1就是12，6+6=12。（男生还在迟疑中）

师（干预）：如果不想得数可以吗？6减1得5，5+7比6+7少1呢。

（3）比比谁能最快说出得数比6+7大1的算式。

男：（抢着说）6+8。

男：（有点激动）因为8比7大1，6一样的，6+8肯定比6+7大。（女生慢了一拍，男生胜）

师：非常棒！根据6+7你还想到比它大2的算式吗？比它小2的算式呢？和同桌说一说。

游戏4：和同桌拿出一张口算卡片，比一比谁的得数大

在加法表中指着算式让学生报得数，比比谁算得快，学生虽然能很快报出得数，但是这与思考无关，他们只要看行数旁边写的得数就可以快速报出得数。更为重要的是，单个的算式计算并不能体现加法表的作用，本节课的重点应是整体的思维，突破之前的凑十法，关注算式间的关联，在关联中感悟加法运算律，即一个加数不变，另一个加数增加几，得数也会增加几的规律，再在运用中进一步理解运算律，提升推理能力。

图6

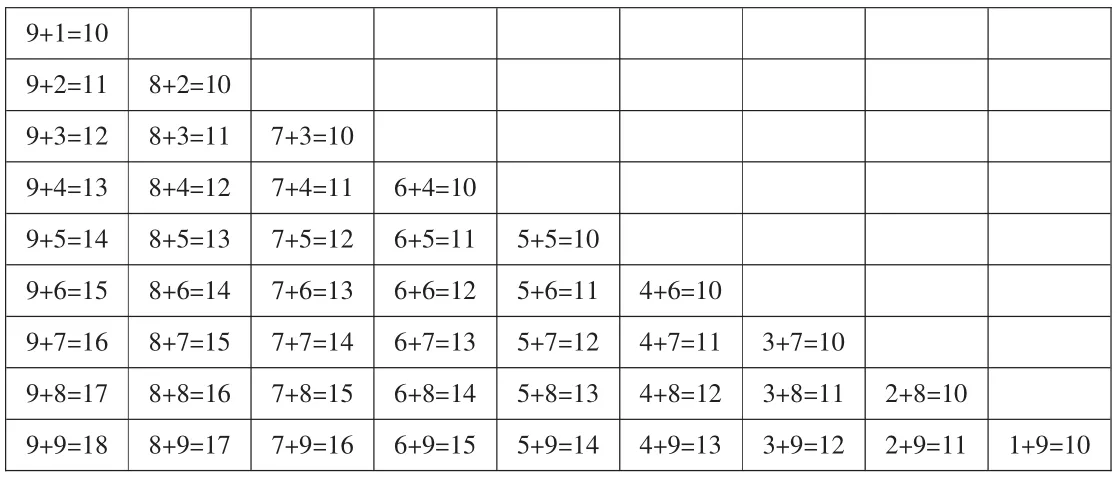
图7

游戏，是低年级学生的精神食粮，用游戏的奇趣元素将推算活动包装起来，可以激发学生的挑战热情，将思维调整到最佳状态。他们在抢答、说理由、评价他人的过程中自然互动，教师需要做的就是在过程中进行引导、点拨。引导学生运用之前发现的加法运算定律来简化思考过程，直接通过调整加数的大小来确定得数的大小。游戏，让学生在重复玩耍中了解算式间联系的同时，推算能力也得到训练和发展。

三、丰富算式的内涵联系，延伸思维路径拓展视角，激发创造

【现状】加法表学习后，教师一般会组织学生解决有关加法的实际问题，进一步理解加法模型，若有提升，也只是提升解决实际问题的复杂程度。

【思考】从算式跳跃到解决问题，加法意义的建构并不是本节课的重点。如果将解决的实际问题孤立开来，整理的意义又何在呢？

【实践】活动：由一道算式想起来

师：根据6+7=13，我们可以想出很多算式。小朋友们都知道，加法算式还可以帮我们讲故事呢。（出示下图，学生逐一口答算式）

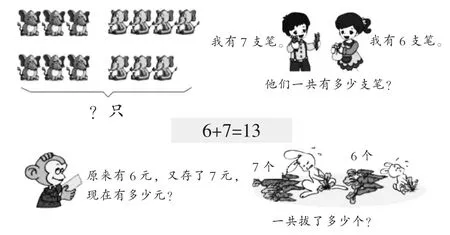
师：为什么这些故事不一样，却都可以用6+7来讲故事呢？

生：它们都是将两个部分合起来，所以要用加法算。

生：它们都是6个和7个，合起来要用加法算。

师：6+7还可以讲什么故事呢？你可以选6+7，也可以在加法表中选另一道式子，讲讲关于这个式子的故事吧。（学生动手写、画）

师：我们看到的是一个简单的加法表，但这些算式却可以讲述着丰富多彩的故事。数学，真是太神奇了。今天我们研究了一个加法表，其实加法表还有不同的样子，我们来看一看。（出示课件，图6、图7）

师：看到这些加法表，你想说什么呢？

生1：算式可以按我们想的顺序放。

生2：这个加法表里的得数斜着是相等的。

生3：这个加法表里多了几道算式，都是等于10的，这几道算式很重要的。

师：整理加法表，可以用多种的方式整理，不同的方式会帮我们看到不一样的秘密。

进位加法表的学习，是帮助学生对20以内的进位加法进行整理、沟通，重新认识的过程。基于一道算式展开联想与回顾，可以从式的联系与式的意义两个角度丰富学生对一道算式内涵的理解。让学生选择加法表中的一道算式研究，鼓励学生发挥想象，理清它与其他算式之间的联系，帮助学生将知识结构化、网络化，利用联想拓宽学生的思维路径，让学生能在脑海中形成“立体”的加法表。呈现得数为10的算式，这样便于学生找到推算的根基。显示得数的加法表，可以让孩子看到相同的得数在一条斜斜的直线上，让他们看到事物存在的多种可能，拓展视野，保持心灵的开放，埋下创造的种子。

数学教学是数学活动的教学，是思维活动的教学，整体思维只是其中的一个部分。我们应通过整理、想象、比较等活动设计帮助学生感悟整体思维，通过独立探索、合作分享等活动帮助学生积累整体思维的经验，从而提升学生以整体视角把握研究对象的能力。