全方位自动导引车的导航与控制系统研究

韩 松，刘晓平，赵云龙，王 刚

(北京邮电大学， 北京 100876)

引 言

随着电子商务的蓬勃发展以及人力成本的不断上升，越来越多的电子商务、物流公司建造了自动化的物流仓储中心，自动化和无人化的程度越来越高。目前，越来越多的物流仓储中心在运输、分拣等环节均使用自动导引车(AGV)来取代人力，减少人力成本，提高工作效率。其中，基于麦克纳姆轮[1]的全方位AGV可以实现前后、左右和自转3个自由度的运动。良好的灵活性使得全方位AGV的控制方式更加多样，对不同工作环境和复杂任务的适应能力更强，有很广阔的应用前景。本文以全方位AGV为研究对象，对其导航和控制系统展开了研究。

为了提高AGV运行路径的灵活性和多样性，越来越多的工厂摒弃传统的磁条导引方式，采用无轨的导航方式。同时，国内外学者对不同原理的无轨导航方式进行了深入研究，并取得了良好的应用效果[2-6]。这些方式大致可以分为两类：基于信标的无轨导航和基于航迹推算的无轨导航。其中，基于信标的导航如激光导航、视觉导航等，局部定位精准，但存在实时性和环境适应性不够及易受光线、粉尘因素影响等问题；基于航迹推算的导航多使用IMU(惯性测量单元)或基于编码器的里程计系统定位，无需依赖外部环境，但是会随时间累积测量误差，无法长期单独使用。针对上述问题，本文结合使用两类定位方法，使用多传感器融合算法弥补两者各自缺点，提高定位精度。

此外，针对全方位AGV的运动模型，本文提出了一种使用PID控制进行路径跟踪的算法，并通过实验验证了算法的可靠性。

1 运动学分析

基于麦克纳姆轮的全方位AGV多采用四轮对称布置，如图1所示。

图1 全方位AGV轮系结构简图

麦克纳姆轮轮毂轴线和辊子轴线夹角为α(本文中α=45°)。点or为车体的中心，并以此为原点建立车载坐标系Σor。AGV在坐标系Σor的位姿为Pr=[xryrθr]T，其运动学公式可以表示为：

(1)

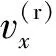
(2)

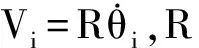
如图1所示，AGV在世界坐标系Σoq的速度可以通过下式进行转换：

(3)

式中：R(θ)为坐标系Σor到坐标系Σoq的坐标变换：

(4)

在车载坐标系下，由式(1)可以求得移动机器人的逆运动学公式：

(5)

2 导航系统设计

2.1 多传感器融合定位

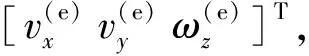
(6)

然而，单独使用基于编码器的里程计进行定位时，由于AGV机械加工过程中的固有缺陷，或受路面打滑等外界因素影响，产生较大的瞬时偏差，且这些偏差会随着式(6)的累积求和不断累加。以此坐标作为定位信息进行导航，容易造成车体向某一方向偏移。所以，需要使用其他可以感知外界环境的传感器对上述定位结果进行校正。

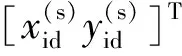
图2 红外图像传感器实物及工作原理

(7)

上述红外定位的方式可以用来消除编码器进行航迹推算造成的误差。考虑到StarGazer的定位可能受到其他红外设备的干扰，如室内的红外监控器，造成检测的错误，所以不能直接使用StarGazer的定位结果取代编码器航迹推算出的位姿。需要采用具有较强鲁棒性的多传感器融合算法，对二者数据进行滤波，得到局部校正的结果。本文使用卡尔曼滤波[7-8]作为融合两种传感器的方法，滤波方法表述如下。

系统的状态方程和观测方程为

(8)

式中：A为状态转移矩阵；B为控制矩阵；H为观测矩阵；wk-1是系统噪声；vk是观测噪声。状态变量选取为：

X=[xyθ]T

(9)

输入变量选取为

u=[vxvyωz]T

(10)

输入变量由里程计系统确定。第k时刻对k+1时刻的预测值表示为：

(11)

其中，

A=I3×3

(12)

控制矩阵B定义为：

B=ToI3×3

(13)

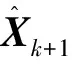
(14)

式中：Zk+1是k+1时刻的实际测量值，测量值选用StarGazer的测量值[x(s)y(s)θ(s)]T；观测矩阵Hk+1取为单位阵I3×3；Kk+1是k+1时刻的卡尔曼增益，通过式(15)得到，其中的P(k+1|k)是k时刻对k+1时刻的预测误差协方差矩阵。

(15)

P(k+1|k)=APkAT+Q

(16)

式中：Q为过程激励噪声协方差矩阵，R为观测噪声协方差矩阵，均为对角阵，分别由编码器和StarGazer的测量误差确定；Pk为k时刻状态变量的误差协方差矩阵。最后，k+1时刻的误差协方差矩阵通过式(17)更新。

Pk+1=(I-Kk+1Hk+1)P(k+1|k)

(17)

经过对里程计航迹推算结果进行线性预测，对齐StarGazer的测量周期Ts，系统每隔Ts使用卡尔曼滤波进行一次传感器融合，其余时刻使用里程计系统以上一次的融合结果为新的初始位姿，单独进行航迹推算，得到每一时刻AGV的定位[xy]T和偏航角θ。

经过多传感器融合，不仅可以消除里程计系统的累积误差，还提高了单独使用StarGazer时的定位频率。在保证实时性的前提下，减小了外界环境对定位系统的影响，提高了定位系统的鲁棒性和稳定性。

2.2 路径跟踪

AGV通过定位和融合算法得到自身在世界坐标系下的实际位姿[xyθ]T，取距离AGV几何中心最近的可微点[xpyp]T作为目标点，如图3所示。图中es、ed和eθ分别表示实际位姿与期望位姿的前向偏差、横向偏差和角度偏差。

图3 路径跟踪示意图

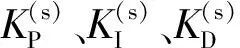
(18)

则根据式(5)可以得到4个麦克纳姆轮的速度为：

(19)

3 实验与分析

本文全方位AGV的机械设计图和实物图如图4所示。

图4 全方位AGV机械设计图与实物图

AGV控制系统结构组成如图5所示，选用固高嵌入式运动控制器作为核心控制器；使用编码器反馈数据和StarGazer红外定位传感器采集到的信息进行传感器融合实现定位和导航；避障传感器用于应对突发情况，保证运行安全；无线手柄用于对AGV进行手动遥控，方便调试和进行紧急控制。

图5 AGV控制系统结构图

使用本文中的卡尔曼滤波对StarGazer和里程计系统的数据进行融合，使用路径跟踪算法对6 m × 4 m的圆角矩形轨迹进行跟踪。实验结果如图6所示，单独使用里程计系统由于定位累积误差过大，无法完成跟踪。图6(a)的点集为进行滤波前单独使用StarGazer进行跟踪的结果，可以看出跟踪效果精度较低，且出现很多间断点和突变点，这是由于红外干扰造成的检测失效；图6(b)的点集为进行数据融合后得到的结果，轨迹平滑连续，更加接近期望的轨迹。

图6 卡尔曼滤波前后路径跟踪效果对比

经过测试，在0.3 m/s的速度下，AGV自动导航的行驶精度可以达到10 mm，且没有位姿检测突变点。最后，对上述算法的运行效率进行了测试，系统进行定位和路径跟踪的频率可以达到15 Hz，满足物流仓储对AGV导航精度和实时性的需求。

4 结束语

本文使用卡尔曼滤波对两种不同机理的传感器进行了数据融合，提出并验证了基于PID控制的全方位AGV的路径跟踪算法。实验证明，融合算法弥补了两种传感器的缺陷，提高了定位精度，滤波器模型可拓展应用于其他种类的定位传感器的融合；路径跟踪算法可靠、实时，具有很高的行驶精度和稳定性，达到了实际应用的要求，离散PID控制器适用于其他结构的全方位AGV的导航控制。

另一方面，由于本文采用原始的卡尔曼滤波模型，对环境中噪声变化的适应能力不够。所以，在后续工作中，将对本文的卡尔曼滤波模型进行改进和优化，提出一种自适应的融合定位算法，实时调整模型的激励噪声协方差矩阵和观测噪声协方差矩阵，进一步提高全方位AGV的定位与导航精度。