改进无监督极限学习机的不平衡数据分类

徐 昌, 陈金琼, 周 文

(安徽师范大学 数学与统计学院，安徽 芜湖 241002)

引 言

近年来不平衡数据分类[1]在分类领域占有越来越重要的地位,严重不平衡的案例极有可能出现在决定性问题中，左右问题处理的走向，从而影响处理的结果。同等分布的数据在预测中是强制的，以避免错误分类[2]。然而，不平衡现象一直是预测问题的主要障碍之一[3]。Wang等人[4]，不平衡数据集创建了不精确的分类模型，特别是对于少数类。此外，Provost等人进行的一项研究[5],指出数据集的比例从一个类到另外一个类可以是一万到十万。之前的一些关于不平衡数据的研究已经开展。不平衡数据的影响出现在电信风险管理[6]、石油泄漏研究[7]、文本识别[8]、蜂窝通信中的欺诈特征[9]和电子垃圾邮件等问题[10]。

为了克服不平衡的数据问题，已经进行了几项早期研究。Batista等人[11]使用一种方法来减少主体群体并增加较小群体，Cristianini等人[12]对类的权重进行了微调，Chawla等人[13]提出一种少类样本合成过采样技术(Synthetic Minority Oversampling Technique,SMOTE)。SMOTE识别难以学习的小类样本数据并剔除，然后根据训练小样本点与最近聚类中心的欧氏距离为其赋予权重，最后按照采样率从小类样本数据中生成合成新样本数据。

模糊c均值聚类(FCM)是一种广泛使用的不平衡数据问题算法。Jain等人[14]基本是研究聚类在没有指定的输出标签的情况下，实现数据的模型构建。FCM是使用隶属度函数确定数据集中每个样本点属于某个聚类程度的一种聚类方法，其中一项研究将基于FCM的算法应用于不平衡数据分类[15]。此外，FCM与支持向量机(SVM)分类的组合优于仅使用分类的模型[16]，同时，在不平衡数据集分类步骤之前，还应用于基于FCM聚类的重新采样非平衡数据预处理方法[17]。

Huang等人[18,19]提出新型的神经网络极限学习机(Extreme Learning Machine,ELM)是受监督的单隐层前馈神经网络(SLFN)。传统的前馈神经网络通常采用基于梯度的算法进行训练，因此需要大量的时间和迭代才能获得最优的参数，并且总存在一些问题，如局部最优，参数灵敏度等。ELM最主要的特点在于随即初始化输入层和隐含层权重，并且直接通过最小二乘估计计算输出权重。在理论和模拟中，ELM不仅克服了传统前馈神经网络的缺点，而且实现更快的速度和更好的泛化性能。ELM是基于最小平方损失函数，在处理不平衡数据时没有得到良好的效果。Huang G等人[20]提出了无监督极限学习机(Unsupervised Extreme Learning Machine，US-ELM)，在没有标记数据可用的情况下，利用未标记的数据探索输入空间的数据结构来提供有用的信息。通过假设输入数据遵循输入空间中的某些簇结构或流形，将未标记数据合并到学习过程中。由于无监督学习更符合现实世界中数据情况，使得无监督学习在数据的分类有效性和合理性方面起着重要的作用。

本文提出了改进的无监督极限学习机。首先，我们对无标签的不平衡数据集进行聚类，分为不同的几个簇，对不同簇上的数据采用五折交叉验证，再将数据进行融合形成训练集和测试集。然后，我们将训练集样本进行模糊c均值聚类，计算出聚类中心和每个样本点的隶属度值，再根据设定的容忍度值迭代新的聚类中心直到终止。这样得到多个聚类中心的不同簇，针对小类样本数据，本文用SMOTE过采样技术增大小类样本数据个数，从而使得小类样本数据个数与大类样本个数近似相等。最后我们将融合后的训练集放入到无监督极限学习机(US-ELM)中训练得到训练模型，再将测试集数据放入到已经训练好的模型中得到最终的分类结果。为了更好的分析本文改进算法的性能，采用对不平衡数据有很好分类效果的GEPSVM[21]、FCM-SVM[22]、FCM-ELM[23]作为对比算法进行试验结果分析。比较了四种算法在数据集Cmc-0-2、Zoos-2-3、Pendigts-0-6、Nursery-2-3、Credit-8-9和page-blocks-0-4上的总体预测准确度(ACC)、灵敏度(SN)、特异性(Spec)和Matthew相关系数(MCC)值。在Cmc-0-2数据集、Zoos-2-3数据集、Pendigts-0-6数据集、Nursery-2-3数据集、Credit-8-9数据集和page-blocks-0-4数据集分别取得了87.23%、92.38%、97.86%、92.27%、89.23%和90.12%的灵敏度(SN)值。SN值主要衡量算法对小类样本分类性能的评价指标，相比与其他三个处理不平衡数据的算法，本文提出的改进算法在SN值上有很好的结果。因此，FCM-US-ELM在处理不平衡数据上有很好的分类性能。

1 理论分析

1.1 无监督极限学习机

(1)

其中λ是权衡参数，β是隐藏层与输出层连接的输出权重，H=[η(x1)T,η(x2)T,…,η(xN)T]∈RN×nh,η(xi)

表示隐藏层相对于xi的输出向量，L∈R(l+u)×(l+u)是标记和未标记数据构建的拉普拉斯算子。注意到上述公式β=0时总是达到最小值。我们必须引入附加约束来避免退化解。具体来说，无监督习机的的公式如下：

(2)

通过选择β作为矩阵，给出(2)的最优解，该矩阵的列是与广义特征值问题的第一个最小特征值问题相对应的特征向量为：

(Inh+λHTLH)v=γHTHv

(3)

其中γ1,γ2,…,γn0+1(γ1γ2…γn0+1)为n0+1个最小特征值，v1,v2,…,vn0+1为其对应的特征向量。我们可以把(2)式改写为：

(4)

其中A=Inh+λHTLH和B=HTH。输出权重β为：

(5)

如果标记数据的数量小于隐藏神经元数量，则(3)未被确定。在此情况下，使用与前面类似的方法，我们有以下的替代公式：

(Iu+λLHHT)μ=γHHTμ

(6)

再次，我们令u1,u2,…,un0+1是对应于(6)式的无最小特征值的广义特征向量，则最终的解为：

(7)

1.2 FCM聚类

根据Ross[24]，FCM基于U矩阵从一组的n个数据点到c类,使目标函数(Jm)进行模糊c均值聚类区分。

(8)

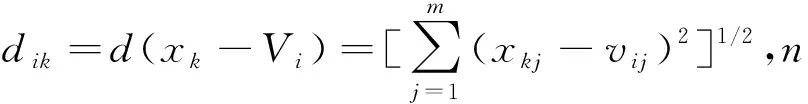
函数uik是第i类中第k个数据点的隶属度函数。同时dik是从点xk到聚类中心vi的欧几里得距离。它可以用一下公式来描述：

(9)

(10)

这里由容忍度值εL来作为迭代停止的标准：

if‖U(r+1)-U(r)‖εL

(11)

1.3 结合SMOTE过采样和FCM的US-ELM分类方法

图1 FCM-US-ELM算法流程图

基于上述理论基础，本文处理的是无标签不平衡数据的分类。首先我们针对不平衡数据我们采用分类前的数据预处理，将不平衡数据通过模糊c均值聚类和SMOTE过采样技术处理为类平衡数据，其次我们将无标签数据放入到无监督极限学习算法中进行训练，得到训练模型再将测试集数据放入已经训练好的模型下，进行分类预测。下面我们给出FCM-US-ELM算法的流程图1。

为了更清楚的表达算法的实现过程，本文给出了具体方法步骤，FCM-US-ELM算法主要分为三个步骤。数据预处理，该步骤是为了得到有效的训练集和测试集，防止因为小类样本个数较少，直接五折交叉可能训练集中没有小类样本数据，训练出的模型对小类样本分类没有作用。训练阶段，将训练集小样本数据个数通过FCM聚类和SMOTE过采样技术增大到与大类样本数量近似相同，以平衡数据集进行模型训练。测试阶段，将测试集放入已经训练好的模型中得到最后的分类结果。具体步骤参见FCM-US-ELM的伪代码，可见算法1。

算法1:FCM-US-ELM

输入： 输入数据集T,聚类中心个数c；

初始化模糊划分矩阵为U0和容忍度值εL

SMOTE采样倍率为P；

US-ElM隐含层节点个数N；

输出：分类结果

数据预处理： 将不平衡数据进行聚类分为两类A和B；

分别对A和B进行五折交叉，整合形成训练集和测试集；

训练阶段：

步骤一： 训练集

2：FCM聚类后各簇数据按照距离聚类重心大小排列，并按顺序输出排列后的数据集；

3：统计聚类后数据集的个数，选出少类样本数据集，并计算出不平衡IR；

4:在少类样本数据集，使用SMOTE过采样，由采样率P，统计距离聚类中心近的样本点，剔除过远样本点。通过线性差值形成新样本，假设x的近邻点为xi，采用如下公式计算：

xnext=x+rand(0,1)×(xi-x)

(12)

其中rand(0,1),表示0～1内的随机数；

步骤二：训练模型

1:得到训练数据：X∈RN×ni，从x构建拉普拉斯算子L；

2:启动具有输入权重的N个隐藏神经元的无监督极限学习机网络，并计算隐藏神经元H的输出矩阵；

3:如果nhN，找到对应于第二个通过n0+1最小特征值(3)的广义特征向量v2,v3,…,vn0+1,

如果nh>N，找到对应于第二个通过n0+1最小特征值(6)的广义特征向量u2,u3,…,un0+1，

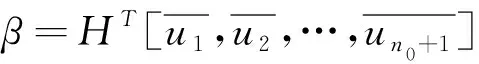
4:计算嵌入矩阵E=Hβ，得到分类模型；

测试阶段：根据训练得到的模型，将测试集放入模型中训练。

2 实验与分析

2.1 不平衡数据集

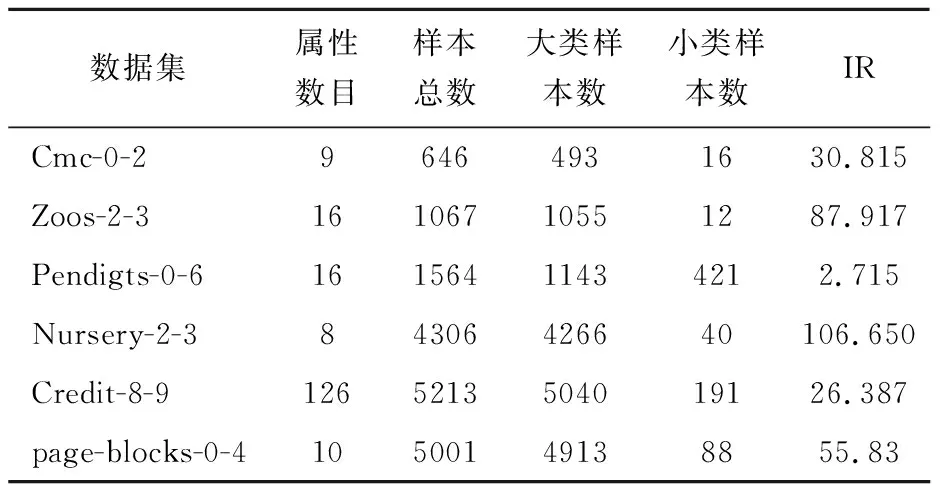
表1 数据集描述

2.2评价指标

为了衡量我们提出的方法的性能，我们重复随机选择训练集和测试集，模型构建和模型评估的过程，并采用五折交叉验证。有四个参数：总体预测准确度(ACC)，灵敏度(SN)，特异性(Spec)，Matthew相关系数(MCC)，定义如下：

(13a)

(13b)

(13c)

(13d)

其中真阳性(TP)是正确预测正类样本点的数量;假阴性(FN)是错误预测负类样本实际为正类样本的数量;假阳性(FP)是错误预测正类样本实际样本点为负类样本的数量，而真阴性(TN)是正确预测负类样本的数量。

2.3 实验设置

在本文中，我们提出的FCM-US-ELM预测器由MATLAB(2017a,Mathworks,Natick,MA,USA)实现。所有的程序都在具有2.5GHz 6-core CPU,32GB内存的Windows操作系统的计算机上执行。US-ELM算法的隐含神经元个数对数据集Cmc-0-2、Zoos-2-3、Pendigts-0-6、Nursery-2-3、Credit-8-9和page-blocks-0-4分别为100、200、250、400、500、500。

2.4 结果与分析

本节中，我们测试了总共六个不同的不平衡数据集，以评估我们提出的方法的性能，例如Cmc-0-2数据集、Zoos-2-3数据集、Pendigts-0-6数据集、Nursery-2-3数据集、Credit-8-9数据集和page-blocks-0-4数据集。首先，我们将数据通过聚类分成两个簇，在整合两个簇的数据进行五折交叉验证，将数据集分成训练集和测试集。其次，我们把训练集样本单独提取出来进行FCM聚类，再用SMOTE过采样技术处理少类样本数据，使得训练集由不平衡数据集变为平衡数据集。最后，我们将测试集放入已经训练好的模型中，得到最终结果。同时为了更好评价改进算法的性能，本文与其他三种处理不平衡数据算法进行了比较，它们分别是GEPSVM[21]、GEPSVM[22]和FCM-ELM[23]。分别比较了四种算法在ACC、SN、Spec和MCC的结果值，具体的结果可以参见图4、5、6、7。在图中，从指标值中我们可以看出本文提出FCM-US-ELM算法可以更好的处理不平衡数据的分类，不仅在整体的分类准确率有很好的性能，尤其在小类样本数据分类准确率上得到了最好的结果。

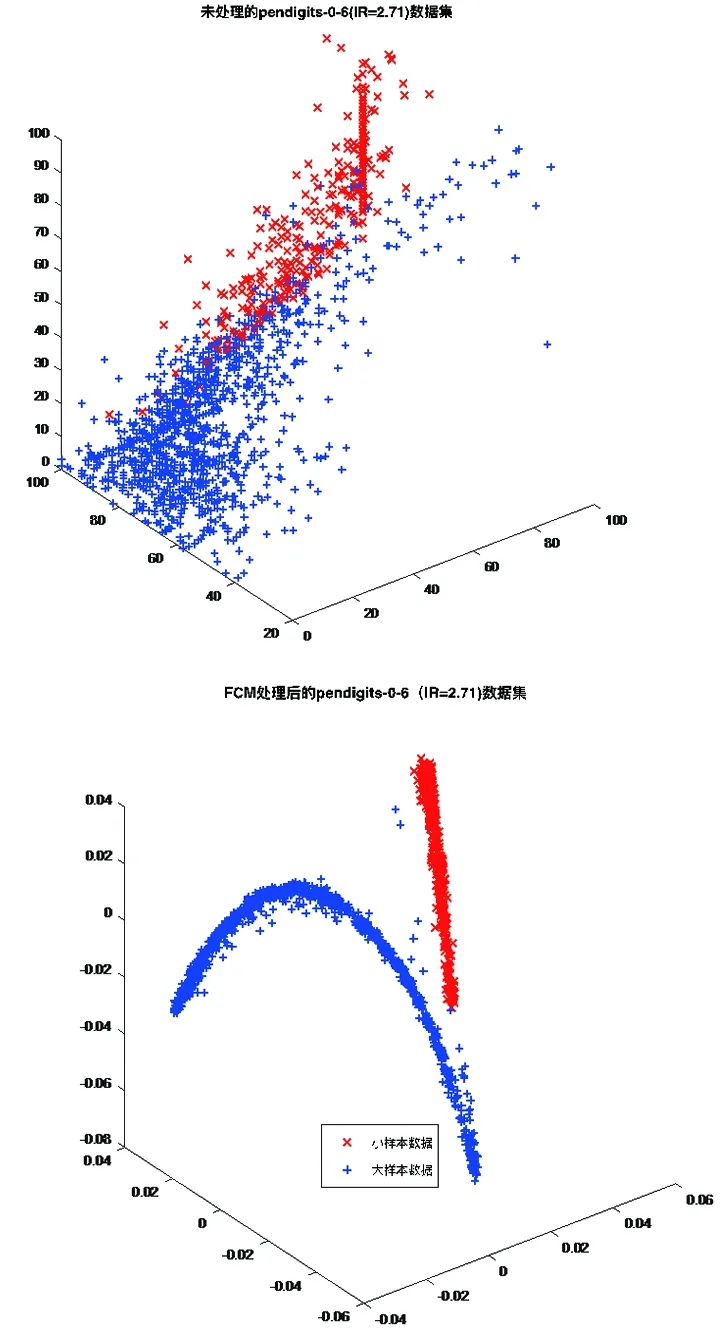
图2 未处理和FCM处理后的Pendigits-0-6数据集

2.4.1 Pendigits-0-6数据集和Pendigits-0-6数据集聚类结果 为了更好的展现FCM在处理不平衡数据的效果，我们给出了Pendigits_0_6、page-blocks-0-4数据集的可视化示例。在图2、3中，原始数据不利于我们将不平衡数据处理为平衡数据，很多数据所属的类别不确定。通过FCM聚类处理后的数据，由聚类中心和隶属度值我们可以更清楚的区分数据所属的类别，得到数据所属的类别后，我们再用SMOTE过采样技术增加正类样本数据个数，从而使得正类样本点个数与负类样本个数接近相同。这样可以避免模型训练时对正类样本的缺失关注，从而抑制过拟合现象的发生。

2.4.2 比较FCM-US-ELM算法与已有算法的指标值 为了更好的展现本文改进算法的性能，我们用FCM-US-ELM与GEPSVM[21]、FCM-SVM[22]和FCM-ELM[23]算法在相同的不平衡数据集上，比较了ACC、SN、Spec和MCC四个指标值。结果如图4、5、6、7所示。在Cmc-0-2数据集上，我们得到了ACC、SN、Spec和MCC的值分别为81.27%、87.23%、81.23%和78.32%。在Zoos-2-3数据集上，我们得到了ACC、SN、Spec和MCC的值分别为89.03%、92.38%、89.01%和83.76%，此数据集小类样本个数仅有12个，FCM-US-ELM得到SN的值为92.38%，是所有算法中值最大的，这也说明本文改进算法在处理不平衡数据集分类上有很好的性能。在Pendigts-0-6数据集上，我们得到的指标值为94.44%、97.86%、93.24%和89.23%，它们分别对应于ACC、SN、Spec和MCC的值。在Nursery-2-3数据集上，我们得到的指标值为92.08%、92.27%、92.13%和87.47%，它们分别对应于ACC、SN、Spec和MCC的值。在Credit-8-9数据集，FCM-US-ELM算法得到的指标值分别为90.61%、89.23%、91.86%和86.72%。FCM-SVM算法在数据集得到更高的91.62%SN值，但改进的算法仍然比GEPSVM和FCM-ELM算法有更高的分类准确率。在page-blocks-0-4数据集上，我们得到了ACC、SN、Spec和MCC的值分别为87.10%、90.12%、87.13%和77.15%。针对不同IR值的数据集，本文提出的改进算法都取得了较好的分类效果，在灵敏度(SN)值上FCM-US-ELM取得比其他三种优秀算法更好的结果。这也说明本文提出的FCM-US-ELM算法能有效地处理不平衡数据集。

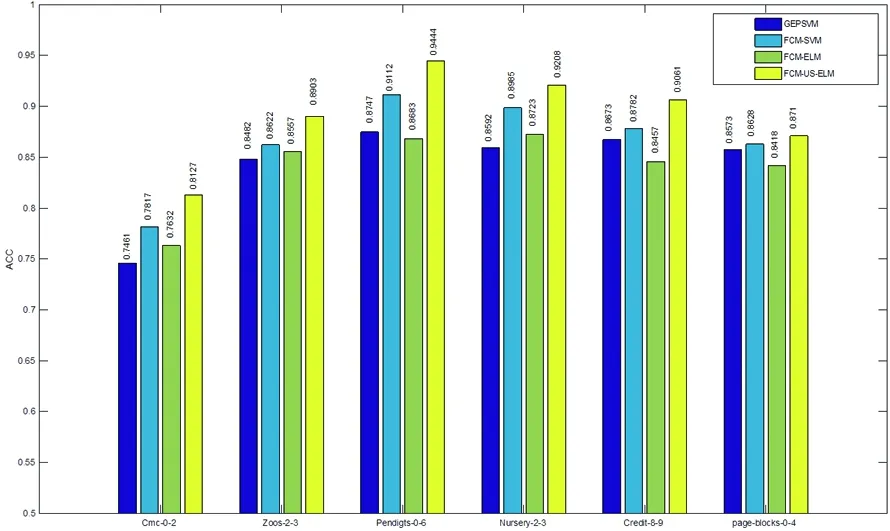
图4 比较不同分类器在六个不平衡数据集上的ACC指标

图5 比较不同分类器在六个不平衡数据集上的SN指标

图6 比较不同分类器在六个不平衡数据集上的Spec指标

图7 比较不同分类器在六个不平衡数据集上的MCC指标

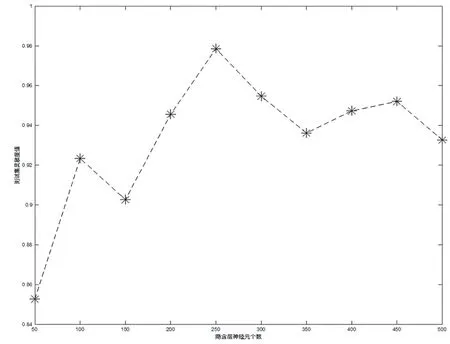
图8 隐含层神经元个数对FCM-US-ELM的性能影响

2.4.3 隐含层神经元个数对FCM-US-ELM的影响 以Pendigts-0-6数据集为例，探索隐含层神经元个数对算法灵敏度的影响。图8所示为隐含层神经元个数对FCM-US-ELM的性能影响，由图可知，并非隐含层神经元个数越多越好，从测试集的灵敏度值(SN)可以看出，当隐含层神经元的个数逐渐增加时，测试集的预测灵敏度值呈现逐渐减小的趋势。因此，我们需要综合考虑测试集的预测指标值和隐含层神经元个数，进行折中选择。

3 结 论

本文针对不平衡数据分类中对少类样本数据分类准确率低的问题，提出了改进的无监督极限学习机算法。首先，我们对无标签的不平衡数据集进行数据的预处理，通过聚类和五折交叉验证的方法将数据集分为训练集和测试集。然后，我们将训练集通过模糊c均值聚类和SMOTE过采样技术将不平衡数据变为平衡数据集。最后，我们将得到的新的训练集放入无监督极限学习机中进行训练，得到训练模型再将测试集放入到模型中，得到最终的分类结果。由上述的实验结果，对比GEPSVM、FCM-SVM和FCM-ELM算法。本文提出的FCM-US-ELM能更好的处理不平衡数据分类，尤其对小类样本数据有很好的分类性能，且在计算时间上也有一定的优势。