薄壁连续箱梁的弯曲自振频率分析

李丽园 周茂定 张元海

(兰州交通大学土木工程学院, 兰州 730070)

现代大跨度桥梁常用的截面形式为箱形截面,而组成箱形截面的各箱壁板厚远小于其截面宽度和高度,具有薄壁杆件的特性[1].薄壁箱梁桥在弯曲荷载作用下存在翼板和腹板的剪切效应,导致其弯曲静力和动力特性的求解较为复杂[2-3].桥梁的弯曲自振特性对于判断桥梁刚度、计算桥梁冲击系数以及分析桥梁的抗震性能有着重要的作用.因此，较为准确地求出箱梁的弯曲自振频率十分重要.

张永健等[4]分析了考虑剪力滞效应影响的简支箱梁弯曲自振特性.甘亚楠等[5]采用2个未知参数分别表示箱梁翼板和腹板剪切变形,建立了弯曲自振频率的控制微分方程,并根据连续梁的边界条件,求解高次微分方程得到相应的弯曲自振频率.周旺保等[6]在此基础上考虑截面的轴向平衡条件,求得考虑剪力滞和剪切变形时的箱梁自振频率.冀伟等[7]将上述一般箱梁的分析理论引入波形钢腹板箱梁,并结合波形钢腹板的特点,分析出适用于波形钢腹板箱梁的弯曲自振频率计算式.以上文献均采用2个未知函数分别考虑箱梁翼板和腹板的剪切变形,且未给出考虑剪切变形影响的等截面连续箱梁自振频率解析表达式.

本文基于薄壁箱梁的弯曲理论,选取一个未知剪切函数来综合表达薄壁箱梁考虑剪切变形影响时翼板和腹板的纵向位移,并以此位移函数为基础,运用三弯矩法求得考虑剪切变形影响的等截面连续箱梁的弯曲自振频率表达式.

1 薄壁箱梁的弯曲总势能分析

薄壁箱梁截面示意图见图1.坐标系为xyz,z为沿梁轴线方向坐标,坐标原点o位于截面形心处.nsz为箱壁中面上的流动坐标系;s为沿箱壁周边的切向坐标;n为沿箱壁周边的法向坐标;ys为形心轴至顶板中面的距离;yx为形心轴至底板中面的距离;b1为顶板中心至腹板中心的距离;b2为腹板中心至翼板边缘的距离;D1为x轴与腹板中面的交点;D2为腹板与顶板的交点;D3为腹板与底板的交点.

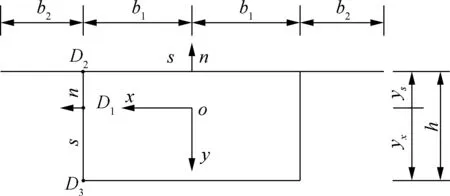
图1 箱梁截面示意图

对薄壁箱梁采用如下基本假设:

1) 小变形条件下,杆件的外形轮廓不变形,即周边不变形;

2) 忽略组成箱梁壁板厚度方向的应变,即τnz=0,σn=0;

3) 各板中面应变εs=0,即箱梁各壁板沿s方向(板平面)切向不可伸缩.

根据如上假设可知,当薄壁箱梁受弯曲荷载时,其剪应变与弯曲剪力流的微分关系如下[8]:

(1)

式中,γ为剪应变;u为箱梁z轴向位移;v为箱梁截面周向位移;q(z)为弯曲剪力流;G为剪切模量;ti为箱梁壁厚.

根据薄壁箱梁的弯曲理论[9]可求得箱梁腹板任意点的剪力流表达式为[10]

(2)

式中,q1(z)为点D1处的剪力流;Q(z)为箱梁剪力;Ix为截面惯性矩;At,Au分别为x轴以上翼板和腹板的面积;tw为腹板厚度.

将式(2)代入式(1),关于s积分整理后可得

(3)

式中,u2(z)为积分起点D2处的纵向位移;v′(z)为v(z)对z的一阶导数.

对于箱梁腹板,截面周向位移v即为箱梁竖向位移w.根据s与y的坐标关系,通过式(3)可将箱梁腹板上任一点的纵向位移表示为

(4)

式中

式中,w′(z)为w(z)对z的一阶导数;u1(z)为D1点的纵向位移.

采用同样的分析方法,根据弯曲剪力流与剪应变关系,在基本假设条件下,可求得分别用D2点和D3点表示的箱梁翼板弯曲纵向位移,具体分析过程参见文献[10],其表达式为

u(x,y,z)=us,x+βζ(x,y)g(z)

(5)

式中

(6)

式中,us,x为顶板、底板与腹板相交点的纵向位移.

箱梁全截面的纵向位移可统一表示为

β(x,y)g(z)+u1(z)

(7)

式中,β(x,y)为全截面广义剪切翘曲位移函数.

考虑截面应力的轴向平衡条件可得

(8)

式中,Fz为截面轴力;σz,εz分别为截面正应力和应变;E为弹性模量;A为箱梁全截面的面积.

将式(7)代入式(8),根据小变形假设可得

u1(z)=-dg(z)

(9)

式中

(10)

式中,Ad,Ac,Ab分别为箱梁顶板、悬臂板、底板的面积.

将式(9)代入式(7)后,将d合并至式(6),可得箱梁截面各点的纵向应变为

(11)

翼板的剪切应变为

(12)

腹板的剪切应变为

(13)

式中,g′(z)为g(z)对z的一阶导数.

由能量原理可得薄壁箱梁的弯曲应变能为

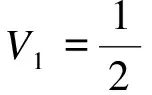
(14)

剪切应变能为

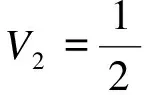
(15)

薄壁箱梁总的弯曲剪切应变能为

G(Ax+Ay)g2]dz

(16)

式中

式中,Ax,Ay分别为翼板和腹板的剪切翘曲面积;Ix为平截面假定下的弯曲惯性距;Iβ为截面翘曲惯性距;Iyβ为截面翘曲惯性距;l为箱梁跨径.

薄壁箱梁的动能主要包括竖向弯曲动能和梁的转动动能.对于一般箱梁,其转动动能很小,可忽略不计[6].因此,箱梁的挠曲动能为

(17)

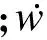
由式(16)和(17)可得

(18)

式中,t1和t2表示任意2个时刻.

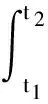
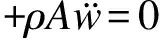
(19)

EIβg″+EIyβw‴-G(Ax+Ay)g=0

(20)

所得自然边界条件为

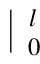
(21)

(22)

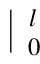
(23)

由此可得简支端的边界条件为

w=0,w″=0,g′=0

固定端的边界条件为

自由端的边界条件为

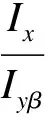
2 控制微分方程的求解

设薄壁箱梁自由振动时的竖向位移函数和剪切变形纵向函数分别为

w(z,t)=w(z)sin(ωt+φ)

(24)

g(z,t)=g(z)sin(ωt+φ)

(25)

式中,ω,φ分别为箱梁自由弯曲振动的圆频率和初始相位角.

将式(24)和(25)代入式(19)和(20),得到关于挠度的微分方程.由于sin(ωt+φ)不恒为零,消去此项并化简微分方程后得

(26)

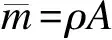
式(26)的特征方程为

(27)

由文献[5]可知,特征方程式(27)的特征解为±λ1i,±λ2,±λ3,从而可得式(26)的通解为

w(z)=C1cos(λ1z)+C2sin(λ1z)+C3cosh(λ2z)+

C4sinh(λ2z)+C5cosh(λ3z)+C6sinh(λ3z)

(28)

式中,C1～C6为微分常数.根据梁两端的3个自然边界条件,可组成6个方程.

对于两端简支的箱梁,6个方程可组成关于C1～C6的齐次方程组.若此方程组有非零解,则系数矩阵行列式的值为零,用MATLAB软件编写相应计算程序得到

(29)

由于λ2≠λ3,且式(29)等式左边中括号内截面特性不为零,故式(29)成立时有

sin(λ1l)=0

(30)

由此可得,λ1=nπ/l,其中n∈N.则简支梁自振圆频率ω的表达式为

(31)

式中

(32)

式(31)较文献[11]中不考虑剪切效应时的弯曲自振频率计算式多了一个an的修正系数.分析式(32)可知,当箱梁截面确定时,an仅受特征值λ的影响.

3 连续箱梁桥弯曲自振频率的分析

对于如图2所示的等截面连续箱梁桥,可在简支箱梁的基础上运用三弯矩法求解.

图2等截面连续梁示意图

由文献[12-13]可知,对于如图2(a)所示的等跨度等截面连续箱梁,其弯曲自振频率的矩阵形式为

(33)

式中

Gm=cothλl-cotλl

式中,Mm为第m个中支点处的弯矩.

对于图2(b)所示的不等跨等截面连续箱梁,设边跨跨径lb与中跨跨径lz的比值为r,即r=lb/lz,其弯曲自振频率的矩阵形式为

(34)

式中

Gmb=cothrλlz-cotrλlz

Gmz=cothλlz-cotλlz

式(33)和(34)为连续梁弯曲自振的三弯矩方程组,据此便可求得等截面连续箱梁的弯曲自振频率.以三等跨连续梁为例，求解其弯曲自振频率.在式(33)中,当中支点处M1=M2=0时,结构的自振特性与简支梁相同,则

(35)

当中支点处的弯矩不为零时,根据式(33)可得

(36)

进而可得

2Gm-Hm=0

(37a)

或

2Gm+Hm=0

(37b)

将Hm和Gm的表达式代入式(37)后可得

2(coshλlsinλl-sinhλlcosλl)-(sinλl-sinhλl)=0

(38a)

2(coshλlsinλl-sinhλlcosλl)+(sinλl-sinhλl)=0

(38b)

运用MATLAB软件求解超越方程式(38a)和(38b),并依照所求解的大小次序排列可得

(39)

将求得的特征解代入式(31) 和(32),便可得到相应的连续箱梁弯曲自振频率.

采用同样的分析方法可求得常用跨数的等跨度连续箱梁桥弯曲自振频率表达式,结果见表1.

对于边跨小于中跨的连续箱梁,只需求得满足式(34)的特征解后,代入式(31)和(32),便可得到不等跨连续箱梁弯曲自振频率.图3给出了三跨和四跨连续梁在不同边中跨径比r时前4阶弯曲自振频率对应的特征解与跨径的乘积λl.

表1 等跨度连续箱梁弯曲自振频率表达式

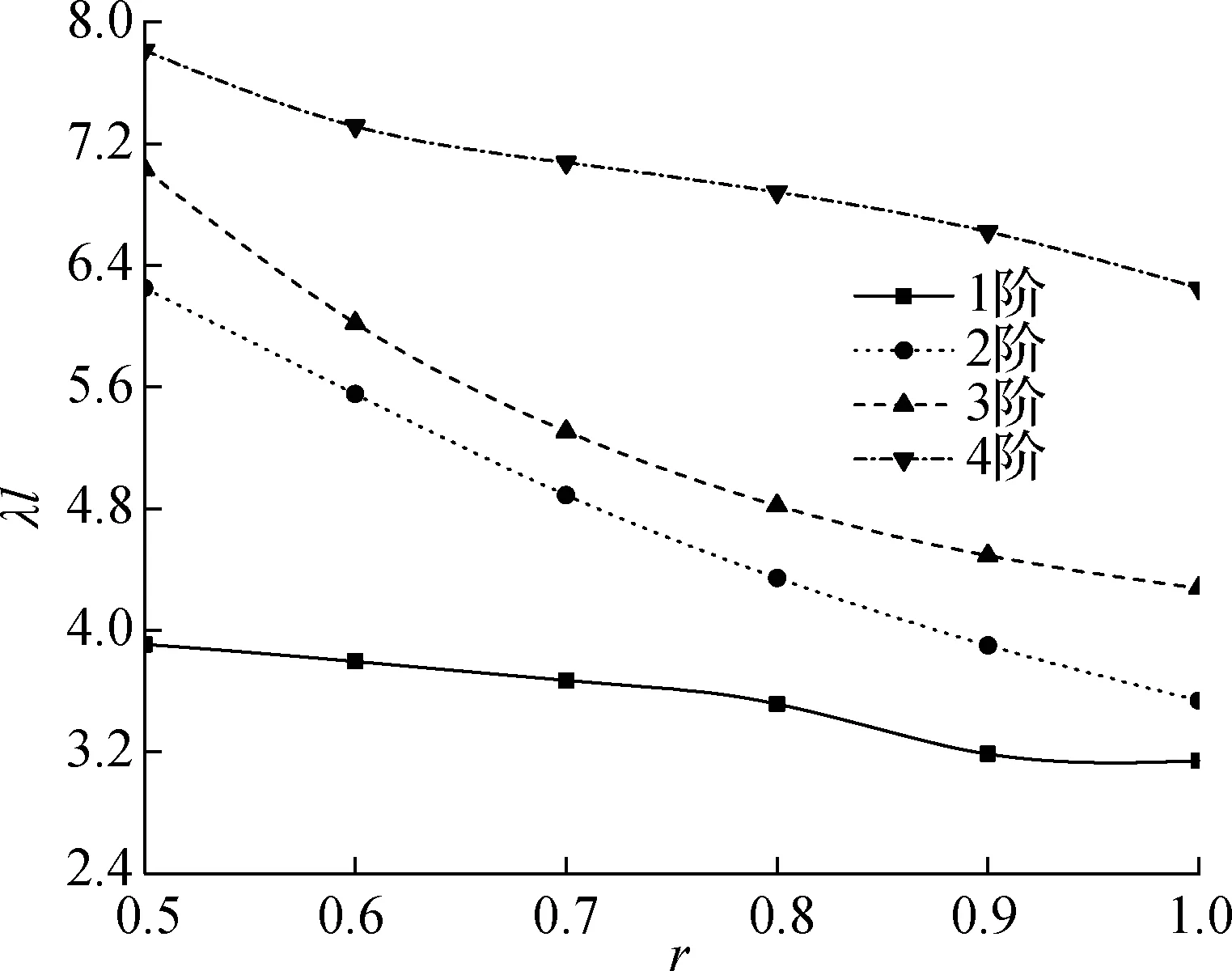
(a) 三跨连续梁

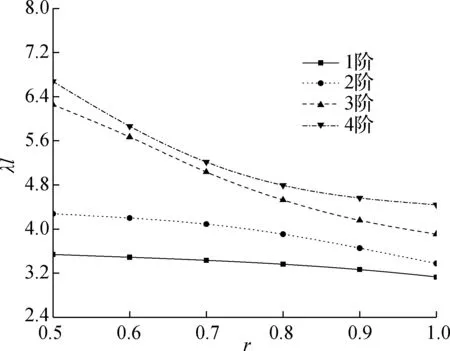
(b) 四跨连续梁

分析图3可知,弯曲自振频率对应的特征解随着边中跨径比的增大而减小,即弯曲自振频率逐渐变大;随着跨数的增加,连续箱梁的弯曲自振频率对应的特征解逐渐减小,即弯曲自振频率减小.

4 数值算例

对于某三跨40 m的直腹板连续箱梁,其材料特性及截面几何参数[5]如下:弹性模量E=35 GPa,密度ρ=2 500 kg/m3,泊松比μ=0.2;各翼板厚度均为0.25 m,腹板厚度为0.40 m,顶板半宽度b1=3.55 m,梁高h=3.75m,悬臂板宽度b2=2.5 m.

分别采用本文方法和ANSYS软件中的beam 189梁单元及shell 63空间壳单元建立有限元模型,计算连续箱梁的前5阶弯曲自振频率,结果见表2.

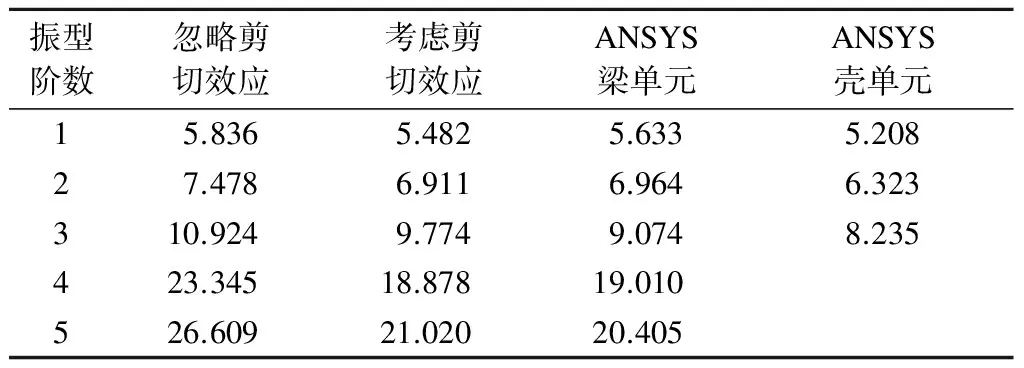
表2 不同方法计算的连续箱梁弯曲自振频率 Hz

由于ANSYS壳单元计算的竖向弯曲频率中高阶振型会掺杂箱壁板的振动因素,故本文只挑选前3阶竖向频率(其他因素影响相对较小)列于表2中.由表可知,本文考虑剪切效应的解析解与考虑剪切效应的ANSYS梁单元及壳单元计算结果吻合良好,从而验证了本文解析解的正确性.剪切效应对箱梁的一阶弯曲频率的影响超过5%,且影响值随频率的增加而增大.

分别按照本文方法、规范公式[11]和ANSYS梁单元计算连续梁弯曲自振频率,结果见表3,箱梁截面特性不变,中跨跨径l=30 m.

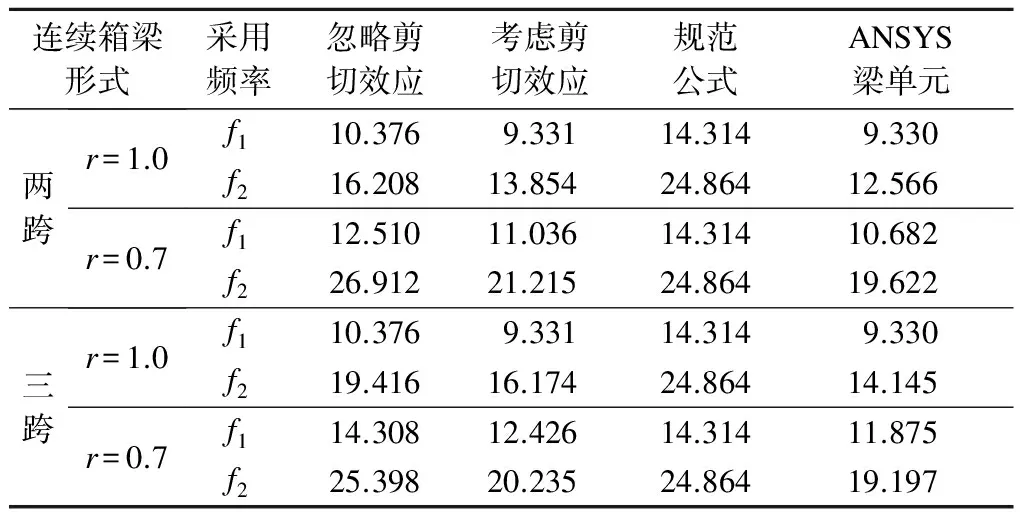
表3 计算冲击时所用连续箱梁的弯曲自振频率 Hz

注:f1和f2分别为连续梁计算跨中和支点冲击所用频率.

考虑剪切变形时的频率差值比ψ为

规范公式与ANSYS计算结果的频率差值比κ为

式中,fh为忽略剪切变形时的弯曲自振频率;fk为考虑剪切变形时的弯曲自振频率;fg为规范公式计算出的弯曲自振频率;fa为ANSYS有限元计算出的弯曲自振频率.

由表3可知,考虑剪切效应的解析解与考虑剪切效应的ANSYS梁单元计算值吻合良好.考虑剪切变形时所计算的频率要小于不考虑剪切变形结果.对于r=0.7时的两跨连续梁,二者频率的差值比ψ=26.85%.按规范公式计算的频率均大于ANSYS有限元计算结果；对于三等跨连续梁,二者频率差值比κ=75.7%.显然,用规范公式计算连续箱梁的自振频率偏大,但这样计算所得的冲击效应也会偏大,对于桥梁设计将偏于安全.

为进一步分析剪切变形对连续箱梁弯曲自振频率的影响,取上述截面的两跨连续箱梁,跨径l取为25～50 m,所对应的高跨比ξ为0.075～0.150,宽跨比η为0.142～0.280.连续箱梁的弯曲自振频率的差值比ψ随高跨比变化曲线见图4.

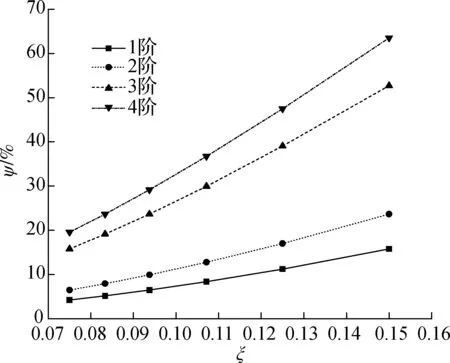
图4 两跨连续箱梁在不同高跨比下的ψ值

由图4可知,随着宽跨比和高跨比的增大,剪切变形的影响不断变大.当η=0.28,ξ=0.15时,1～4阶弯曲自振频率的差值比由15.8%增至63.6%,说明剪切变形对弯曲自振频率的影响随着阶数的增加而增大.因此,计算连续箱梁高阶弯曲自振频率时,剪切变形的影响不可忽略.

5 结论

1) 基于薄壁箱梁的弯曲理论,将箱梁翼板和腹板剪切变形综合为一个剪切翘曲函数,运用能量变分法及Hamilton原理导出并求解箱梁弯曲自振频率的控制微分方程.在简支箱梁弯曲自振频率的基础上,利用三弯矩法,分析出考虑剪切变形影响的等截面连续箱梁的弯曲自振频率表达式.

2) 通过对连续箱梁弯曲自振频率对应的特征解分析可知:随着边中跨比的减小,连续箱梁的弯曲自振频率逐渐增大;随着连续箱梁跨数的增加,桥梁的弯曲自振频率逐渐减小.

3) 按照本文公式计算的连续箱梁弯曲自振频率与ANSYS空间壳单元及考虑剪切效应的梁单元有限元计算结果吻合良好.按本文公式计算简支和连续梁的弯曲自振频率,所得结果精度较高.根据现行公路桥规中所给的频率表达式得到的计算结果偏大,但若用其计算冲击效应时,计算结果将会偏于安全.

4) 考虑剪切变形影响所计算的箱梁弯曲自振频率小于不考虑剪切变形的结果,且频率阶数越高,差值越大.随着箱梁高跨比和宽跨比的增大,剪切变形的影响也会变大.在计算连续箱梁高阶频率时,剪切变形的影响不可忽略.

)

[1] 包世华,周坚. 薄壁杆件结构力学[M]. 北京:中国建筑工业出版社,2006:1-20.

[2] Zhou S J. Shear lag analysis in prestressed concrete box girders [J].JournalofBridgeEngineering, 2011,16(4): 500-512.DOI:10.1061/(asce)be.1943-5592.0000179.

[3] Zhang Y H. Improved finite-segment method for analyzing shear lag effect in thin-walled box girders [J].JournalofStructuralEngineering, 2014,138(10): 1279-1284.DOI:10.1061/(asce)st.1943-541x.0000552.

[4] 张永健, 黄平明. 考虑剪力滞效应的简支箱梁自振特性[J]. 建筑科学与工程学报, 2005, 22(2): 40-42. DOI:10.3321/j.issn:1673-2049.2005.02.007.

Zhang Yongjian, Huang Pingming. Free vibration characteristics of simply supported box girder with effect of shear lag[J].JournalofArchitectureandCivilEngineering, 2005,22(2): 40-42. DOI:10.3321/j.issn:1673-2049.2005.02.007.(in Chinese)

[5] 甘亚南, 周广春. 基于能量变分原理的薄壁箱梁自振特性分析[J]. 中国公路学报, 2007, 20(1): 73-78. DOI:10.3321/j.issn:1001-7372.2007.01.014.

Gan Yanan, Zhou Guangchun. Analysis of free vibration characteristics of thin-walled box girder based on energy variation principle[J].ChinaJournalofHighwayandTransport, 2007,20(1): 73-78. DOI:10.3321/j.issn:1001-7372.2007.01.014.(in Chinese)

[6] 周旺保, 蒋丽忠, 戚菁菁. 考虑剪力滞和剪切变形的薄壁箱梁自振特性分析[J]. 计算力学学报, 2013, 30(6): 802-806. DOI:10.7511/jslx201306009.

Zhou Wangbao, Jiang Lizhong, Qi Jingjing. Analysis of free vibration characteristic of thin-wall box-girder considering shear lag and shear deformation[J].ChineseJournalofComputationalMechanics, 2013,30(6): 802-806. DOI:10.7511/jslx201306009.(in Chinese)

[7] 冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板组合箱梁振动频率分析与试验[J]. 中国公路学报, 2013, 26(5): 102-107. DOI:10.3969/j.issn.1001-7372.2013.05.014.

Ji Wei, Liu Shizhong, Lin Pengzhen. Experiment and analysis for vibration frequency of composite box girder with corrugated steel webs[J].ChinaJournalofHighwayandTransport, 2013,26(5): 102-107. DOI:10.3969/j.issn.1001-7372.2013.05.014.(in Chinese)

[8] 张元海, 白昕, 林丽霞. 箱形梁剪力滞效应的改进分析方法研究[J]. 土木工程学报, 2012, 45(11): 153-158.

Zhang Yuanhai, Bai Xin, Lin Lixia. An improved approach for analyzing shear lag effect of box girders [J].ChinaCivilEngineeringJournal, 2012,45(11): 153-158. (in Chinese)

[9] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版.北京:人民交通出版社, 2008: 1-60.

[10] 周茂定, 李丽园, 张元海. 考虑剪切变形时薄壁箱梁的挠曲分析[J]. 工程力学, 2015, 32(10): 138-144.

Zhou Maoding, Li Liyuan, Zhang Yanhai. Flexural analysis of thin-walled box girders with shear deformation [J].EngineeringMechanics, 2015,32(10):138-144. (in Chinese)

[11] 中华人民共和国交通运输部.JTG D60—2015 公路桥涵设计通用规范 [S]. 北京:人民交通出版社, 2015.

[12] 杨茀康.结构动力学[M].北京: 人民交通出版社, 1987:252-261.

[13] 高庆飞. 移动车辆荷载作用下梁式桥动力性能设计与评价方法 [D]. 哈尔滨: 哈尔滨工业大学交通科学与工程学院, 2015.