考虑剪力滞效应的薄壁曲线箱梁自由振动的有限段法

2018-02-08罗旗帜周旭辉

佛山科学技术学院学报（自然科学版） 2018年1期

张琪，罗旗帜，周旭辉

（1.佛山科学技术学院交通与土木建筑学院，广东佛山528000；2.上海市政工程设计研究总院（集团）广东有限公司，广东深圳518040）

混凝土薄壁箱梁以其良好的抗扭性能而广泛应用于曲线桥梁工程中。薄壁曲线箱梁是空间结构，既存在弯扭耦合作用，又受剪力滞效应的影响，故其受力性能分析比直线箱梁更复杂。桥梁的服役寿命除依赖其静力性能外，更依赖于桥梁结构在车辆荷载作用下的动力工作性能。近年来，国内外学者对曲线箱梁结构剪力滞效应的静力分析已作了较深入地研究［1-3］，其计算理论日趋完善，部分研究成果已被应用于设计中。但对于薄壁曲线箱梁剪力滞效应的动力分析及研究还处于初始阶段。要比较全面、准确地了解薄壁曲线箱梁的动力特性，目前最常用的方法是数值法，特别是空间有限元法［4-6］；而解析法或半解析法应用于此类问题的动力分析见诸报导不多。与数值法相比，解析法或半解析法具有更重要的理论价值，计算量少，便于工程应用，能更好地揭示动力特性以及各参数之间的内在关系。文献［7］基于能量泛函变分原理，得到考虑剪力滞效应影响的曲线箱梁自由振动微分方程，并采用分离变量法获得简支曲梁的自振频率。文献[8］在能量法基础上，进一步假设位移场函数，获得了自振频率显示解，并分析了剪力滞效应对于曲线箱梁自振频率的影响。但文献［7］、［8］方法仅限于简支曲线箱梁。文献［9］提出了一种曲线箱梁桥动力特性分析的有限段元法，采用多项式插值函数作为单元内部的位移函数，获得自振频率的近似解，但离散单元仍较多。作者曾提出了薄壁箱梁剪力滞动力特性分析的有限段法［10］，研究了多跨连续直线箱梁剪力滞效应对自振频率的影响，并与有限元法作了比较，结果吻合较好。

本文将考虑剪力滞效应的直线箱梁动力分析的有限段法推广到曲线箱梁中去。以能量泛函变分原理获得的曲线箱梁剪力滞控制微分方程的齐次解为位移模式中的峰值函数，提出了一种半解析的有限段计算方法，将空间结构简化为杆系结构。文中给出了连续曲线箱梁算例，其结果与有限元解法作了比较，证明本文方法的正确性。

1 基本假定

曲线箱梁的横截面尺寸和坐标系统如图1所示，荷载作用如图2所示。曲线箱梁在竖向分布荷载和分布扭矩作用下会产生竖向弯曲和扭转。

基于薄壁结构理论，有以下假定:

（1）忽略初曲率的影响；

（2）曲线箱梁处于弹性工作阶段；

（3）曲线箱梁腹板中的应力可由初等梁理论确定，仅计算腹板的弯曲应变能；

（4）不考虑翼板的横向变形、竖向挤压变形以及板平面外的剪切变形，即（εx=εy=γzy=γxy=0）；

（5）曲线箱梁自由振动时，箱梁的悬臂板、顶板以及底板剪力滞翘曲动位移函数可以假设为［1］

图1 曲线箱梁

图2 曲线箱梁荷载示意图

根据以上假定，曲线箱梁翼板的正应变，除了服从平截面假定的刚性截面均匀位移产生的正应变εz1外，还需补充由剪力滞翘曲位移产生的正应变εz2，即

式（2）中，kx为梁轴线处的曲率。

2 位移模式

薄壁曲线箱梁梁段单元在自由振动时，各质点作简谐运动，梁段各节点动挠度、动扭转角以及动位移差函数的位移模式可以假设为［8］

式（3）位移模式中ω为曲线箱梁的自振频率，θ为曲线箱梁自由振动的初始相位角，峰值函数v（z）、φ（z）、ξ（z）采用了梁段单元控制微分方程的齐次解。基于有限元原理，可沿跨径方向将曲线箱梁分为若干段，如图3所示的梁段单元，其两端除具有直线箱梁［10］的挠度v、转角v'以及纵向位移差函数ξ三个未知量外，尚需补充扭转角φ和φ'扭率，共同描述曲线箱梁的梁段位移。曲线箱梁梁段位移模式中的峰值函数取以下表达式［1］

式（4~6）中，A1，A2，A3…A10为积分常数；F3，E3，T3，H3，S1，S2是与截面尺寸、材料特性和曲率半径有关的参数。

图3所示的梁段单元，其节点位移参数取为

当z=0时，vi（0）=vi，vi'（0）=vi'，φi（0）=φi，φi'（0）=φi'，ξi（0）=ξi。当z=s时，vj（s）=vj，vj'（s）=vj'，φj（s）=φj，φj'（s）=φj'，ξj（s）=ξj，将式（7）写成矩阵形式

式（8）中，［H］、［N］、［P］为上述位移模式中的形函数；｛δ｝e为节点位移列阵。

将式（8）代入式（3），可将位移模式写成矩阵形式

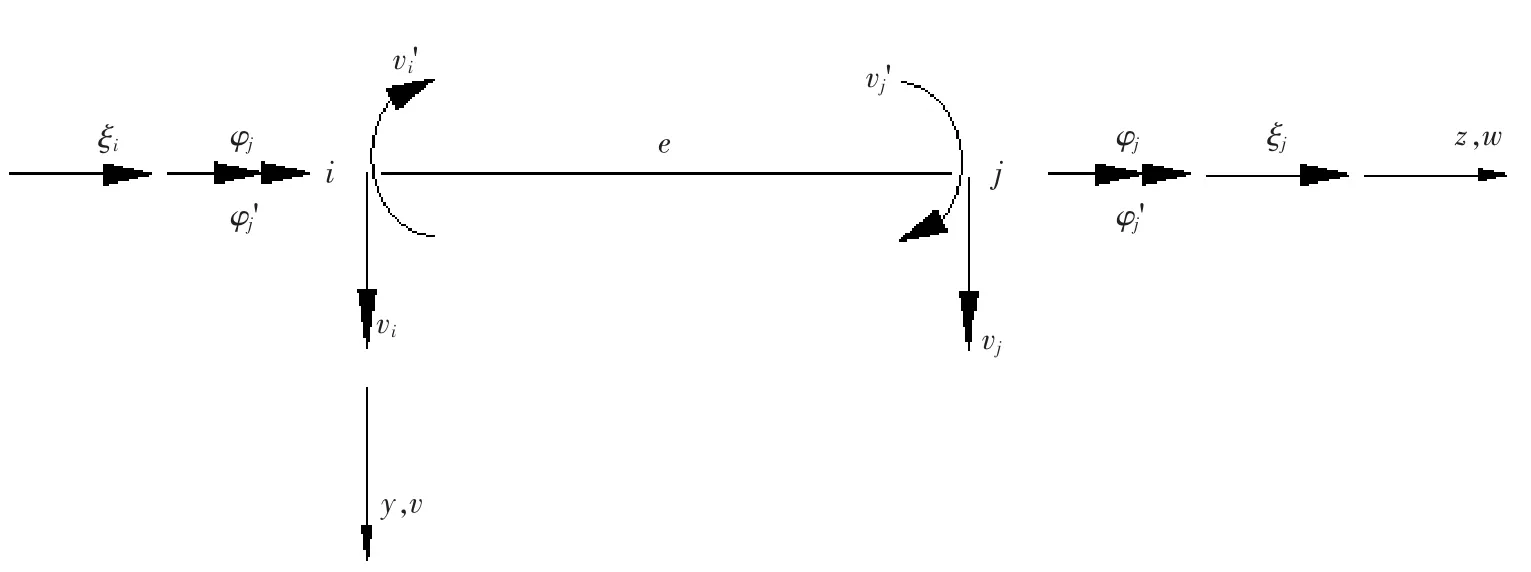
图3 梁段单元

3 自振方程

3.1 梁段单元总势能

按照前述假定，应用能量法求得薄壁曲线箱梁考虑剪力滞效应的总势能为

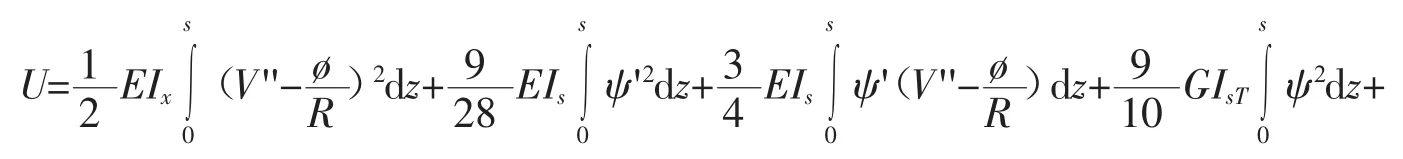
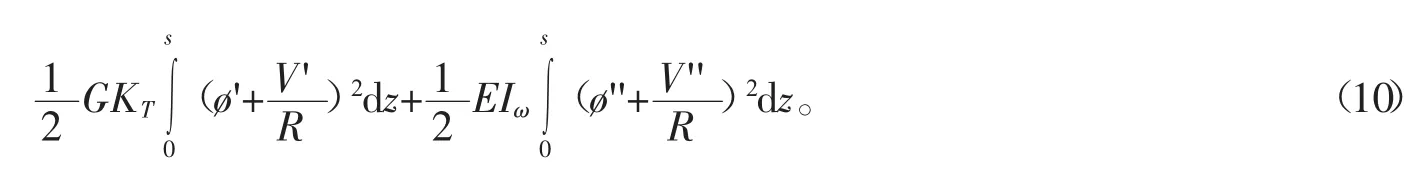
式（10）中，E、G 分别为曲线箱梁的弹性模量和剪切模量；Ix、KT、Iω、Is、IsT分别为曲线箱梁任一截面的抗弯、抗扭、扇形、翼板以及广义惯性矩，其中Is和IsT的表达式分别为

3.2 梁段单元总动能

梁段单元竖向振动时，动能可以表示为

其中，ρ和A分别表示曲梁的密度和横截面积。

3.3 自振方程

将式（9）代入式（13），转化为矩阵形式并对｛δ｝e进行一阶变分，由于位移变分的任意性且 δ｛δ｝eT≠0，得

其中，ω为曲线箱梁的自振频率，｛δ｝e为与自振频率相对应的各阶振型。公式（14）即为考虑剪力滞效应的薄壁曲线箱梁无阻尼自由振动方程：（［K］e-ω2［M］e）｛δ｝e=｛0｝。

由式（14）得到的单元刚度矩阵［K］e和质量刚度矩阵［M］e如下

通过矩阵组合，将单元刚度矩阵和单元质量矩阵集合成总体刚度矩阵和总体质量矩阵，再利用子空间迭代法求解广义特征值问题，即可获得曲线箱梁的各阶自振频率和振型。本文采用Matlab软件进行编制程序。

4 对比与分析

4.1 结果对比

取三等跨连续梁分析，跨径组合为15 m+15 m+15 m，曲梁半径R=30 m，两端为抗扭支承，中间为点支承，计算简图如图4示，横截面如图5，其材料力学参数和几何参数分别为：弹性模量E=3.5×104MPa，泊松比 μ=0.3，密度 ρ=2 500 kg/m3，顶板厚 t1=0.25 m，悬臂板厚 t2=0.25 m，底板厚 t3=0.25 m，腹板厚 tw=0.4 m，半顶板宽b1=2.55 m，悬臂板宽b2=2.55 m，半底板宽b3=2.55 m，梁高hw=3.0 m。

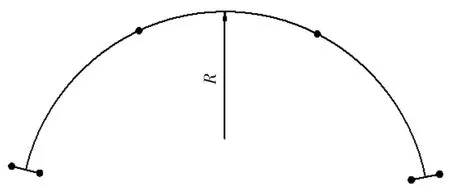
图4 连续曲梁计算简图

图5 横截面尺寸（单位：m）

将材料力学参数、桥梁跨径以及截面尺寸等导入自编计算程序，运用子空间迭代法便可获得前三阶竖向自振频率。有限元模拟采用Ansys中的solid45（8节点实体单元）进行建模分析，节点数为9 768，单元数为4 959，两种计算方法得到的曲线箱梁竖向自振频率如表1所示。

表1 频率计算结果

从表1中可知，本文解法得到的各阶频率与有限元结果相比吻合较好，证明了本文方法的正确性。

4.2 影响参数分析

研究表明曲线箱梁的宽跨比、曲率半径等是影响剪力滞效应的重要参数［1］，本文重点探讨了宽跨比和曲率半径对曲线箱梁自振频率影响的变化规律。曲率半径分别取为30 m、60 m、15 m，宽跨比（按文献［1］定义）分别取为0.085 m、0.106 3 m、0.17 m，箱梁计算图示和横截面同图4和图5。本文计算结果与初等梁理论（不考虑剪力滞效应）值作了比较，自振频率计算结果见表2。

从表2可以看出：1）考虑剪力滞效应后，曲线箱梁前三阶自振频率均有不同程度的减小；2）当曲率半径不变时，随着宽跨比的增大，曲线箱梁的剪力滞效应对自振频率的影响越大；3）当宽跨比不变时，随着曲率半径的增大，曲线箱梁剪力滞效应对自振频率的贡献率也增大，但增大幅度比宽跨比的影响小。