综合满意度评价出租车动态定价模型

程延强，陈金鹿，李俊辉，许文德

（1.吉林大学珠海学院国际贸易与金融系，广东珠海519041；2.吉林大学珠海学院电子信息系，广东珠海519041）

1 问题分析

出租车的定价问题，实际上是如何基于乘客和司机的双方利益，对影响出租车价格的主要因素进行合理调控的问题，参考的评价指标是乘客和司机对于某一单的综合满意度。根据Uber的最新研究［6］，在相同环境变量下，采用动态定价的打车方式时，打车成功率高达100%，这在一定程度上表明了动态定价机制的高效性，但是由于Uber价格算法仅考虑供求关系对价格的影响，并没有充分考虑乘客的购买承受力，例如巴黎恐袭，案发所在地Uber价格瞬间涨了4倍，这引起了乘客的强烈不满。由此可见，动态定价不仅要考虑司机的利益，同时也要充分考虑乘客的满意度。本研究先通过最短距离算法获得出租车在恒速下到达目的地的驾驶时间，然后提出由乘客和司机妥协后的最佳交通灯等待时间模型，即可得到该单的预估最佳驾驶时长，若超过该时长，每超过1 min，单价将以ω元/min的速度下降，直到超过预估最大时长或每分钟的单价降为0元，则停止计费；同时分别考虑该乘客所在区域内的出租车供给量和接单司机所在区域内的订单需求量，构建供求比调节价格的分段函数。综上，得到由司机和乘客折中后的动态定价模型，如图1所示。随后通过构建司机满意度模型和乘客满意度模型，利用司机满意度和乘客满意度互斥关系，构建综合满意度作为评价指标，从而证实本文模型的高效性、高灵敏度。

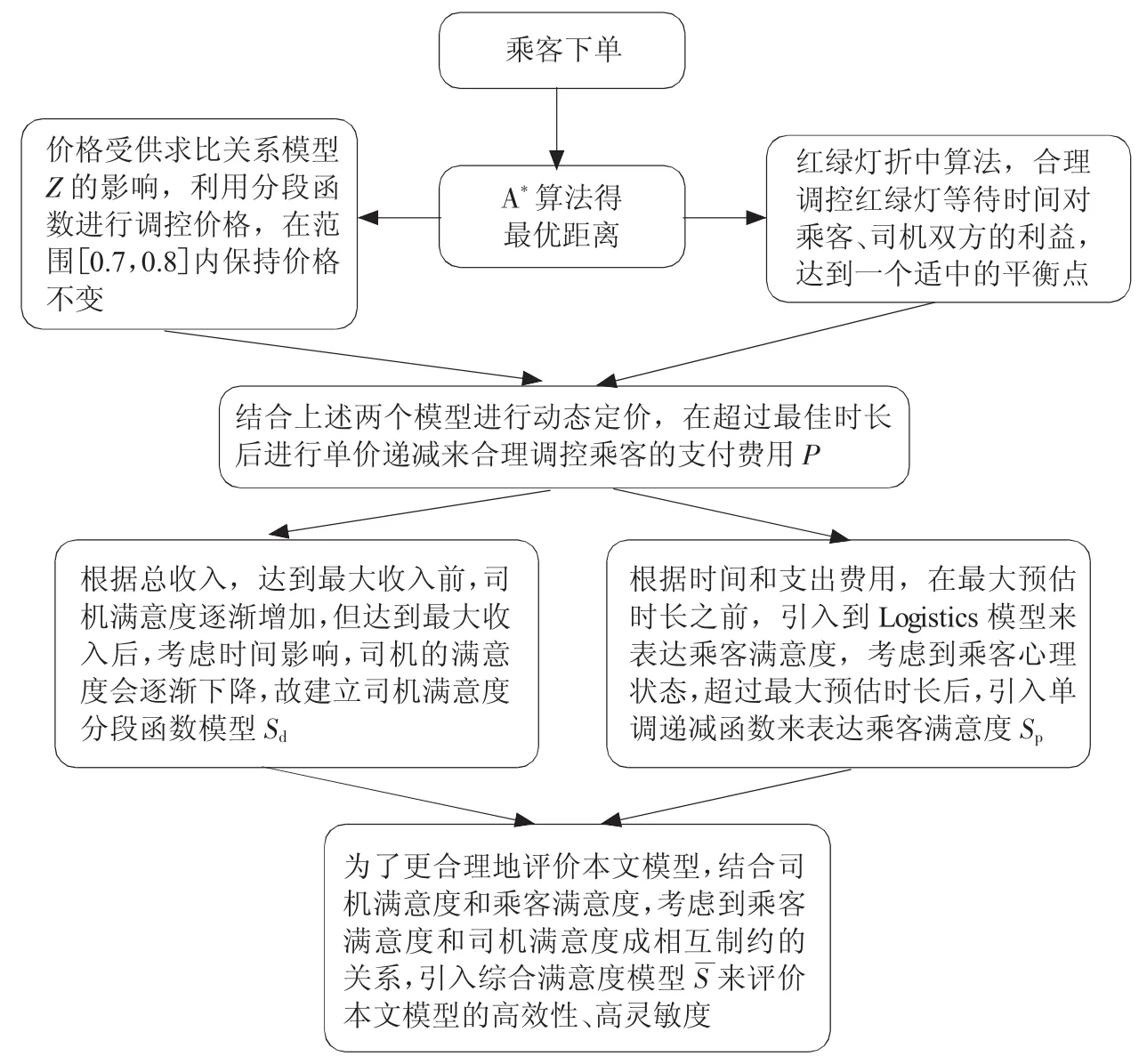
图1 动态定价模型的流程图

2 供求关系影响价格的分段函数

2.1 供求关系模型

根据文献［7］，我们引入出租车司机愿意接单半径R=2 km。

以某乘客为圆心，以R为半径，该圆区域内的全部出租车数量M作为该单的出租车供给量；以该区域内的每位出租车司机为圆心，以R为半径，在每位司机对应的圆区域内的下单量作为该单的出租车需求量Q。因此，对于某一单的供求比为：

2.2 供求比对价格的影响模型

根据文献［8］，出租车最佳供求比在［0.7，0.8］范围内，于是引入了经济供求曲线，当出租车供不应求时，适当给司机涨价，而当供过于求时，适当降价，从而实现动态控制价格并促进资源配置。基于Uber的动态调价算法，笔者调研了供求比范围在［0，3］的1 200个订单，通过数据挖掘获取在Uber动态定价下的费用，通过模拟仿真得到无动态定价下对应的费用，两者的差值即为动态调价的幅度，统计分析后发现双方对供求比调价的期望值基本上落在如图2所示的两线附近。供求比在［0.7，0.8］范围内对车费无影响，当供求比越接近0，则对司机的涨价幅度越高，但每单涨价不超过15元，当供求比大于0.8，则对该单的降价幅度越大，但不超过15元。

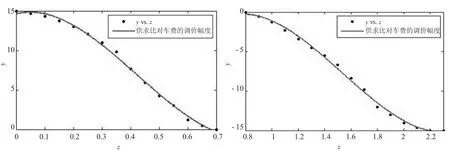
图2 供求比对每一单价格的影响曲线

经过数据拟合，得到供求比对每一单价格的影响曲线为

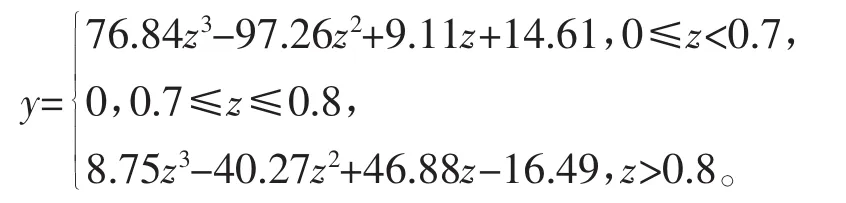
3 综合动态定价模型

3.1 红绿灯折中算法

设后台规划好的最短路径上的交通灯个数为N，N≥0，出租车在某一单的驾驶过程遇上红灯的个数为N'，0≤N'≤N，由于不同路口的交通灯周期不同，设最佳路径上各交通灯的红灯周期为，考虑到乘客和司机双方的利益，从心理学的角度，取每个红灯周期的均值作为出租车每次遇上红灯时需要等待的时长。通过实地场景调研，发现出租车在恒速下平均遇到红灯的个数为，而遇到红灯的最多个数为，因此驾驶过程中，等待交通灯的最佳预计时长为当司机某一趟遇到红灯的个数最多，且每次平均等待的时长均为时，达到最长等待时长

3.2 动态定价

软件后台根据乘客始末位置规划的最短路径上的路程为S，出租车全程速度恒定为v，则预估到达目的地的最短时长为单位为分钟。

实验鱼采用天津鑫达鱼苗繁育基地人工孵化的麦穗鱼幼鱼，共503尾，全长35.9±3.3mm，体重为5.8±1.7g。提前半个月将试验鱼放入实验水槽内暂养，以便其适应实验环境从而提高实验准确性。

当司机所花时长超过tbest，则往后每分钟的单价将服从斜率为ω线性减函数，对于每一单驾驶时长的峰值越大，则ω越大，根据不同订单的价格属性，引入物理运动学的理论来定义即往后每分钟的单价为其中，Pk为超过tbest后每分钟的单价，k为超过最佳预估时长分钟数，且k的值向前取整，单位为分钟。

则每一单的预估车费模型为

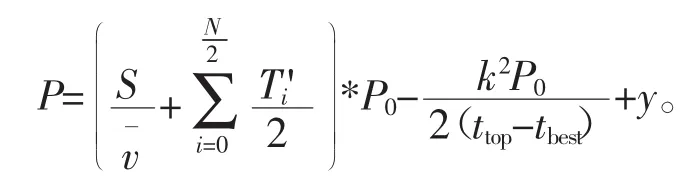
4 模型验证

4.1 司机满意度模型

当司机驾驶时长小于ttop（最大预估时间）时，收入未能达到峰值Ptop，而当驾驶时长大于ttop时，虽然收入达到峰值，但是时间成本在增加。司机对某一单的满意度Sd与驾驶时间t的关系如图3所示。

司机的满意度模型为

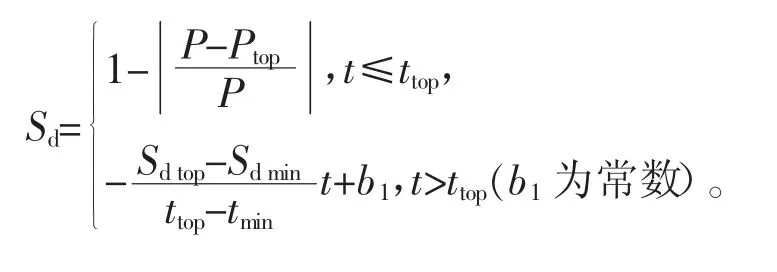
4.2 乘客满意度模型

对于乘客，如图4所示，当t≤tmin时，乘客满意度趋近于1，当tmin≤t≤ttop时，由红绿灯调价后的乘客满意度下降幅度较大，因此该过程乘客满意度满足Logistic曲线；当t≥ttop时，虽然车费不再增长，但根据乘客的打车心理，最终车费和期望车费的变化趋势以及驾驶时间均会影响乘客的满意度，于是通过建立递减的一次函数用于动态模拟乘客的满意度，即乘客对该单的满意度模型为

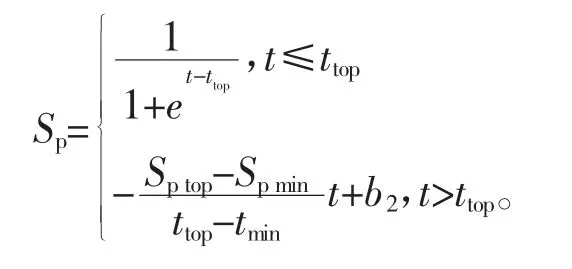
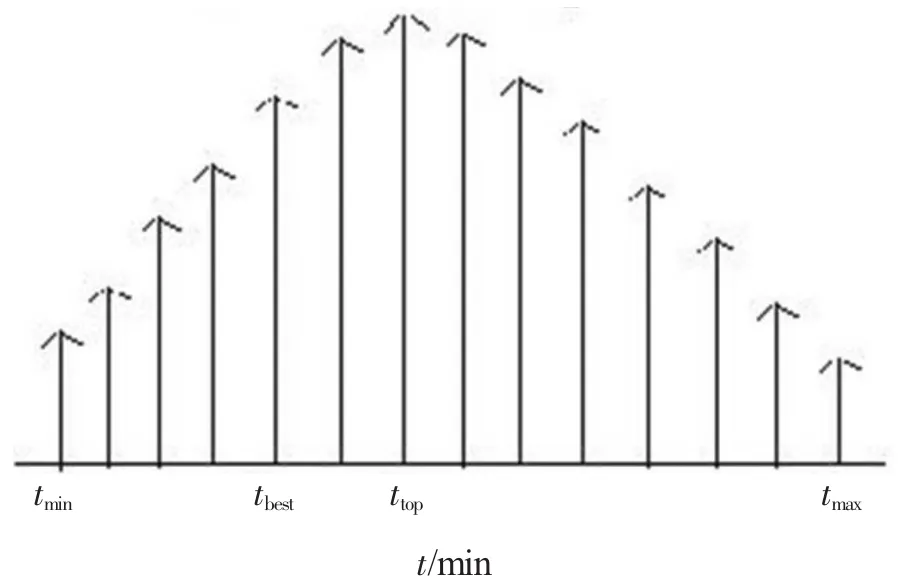
图3 司机的满意度评价指标

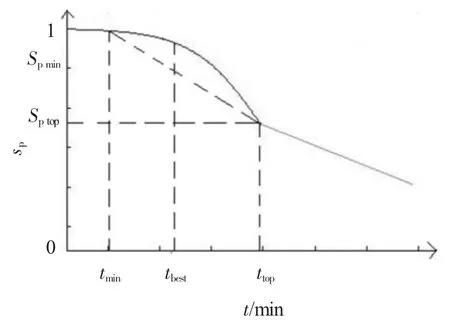
图4 乘客的满意度评价指标

4.3 综合满意度评价模型

由于驾驶过程每个时刻的司机满意度和乘客满意度是一一对应的，同时司机的收入全部来源于乘客，故乘客满意度和司机满意度互斥。即某个时刻下双方的综合满意度模型为

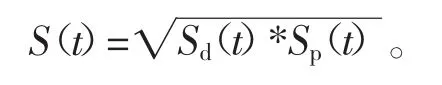
为了更准确地描述每一单的综合满意度，考虑了驾驶过程到达目的地的时间概率分布情况。通过大量的市场调研，我们发现不同属性的订单到达目的地的时间概率分布服从正态分布，如图5所示。

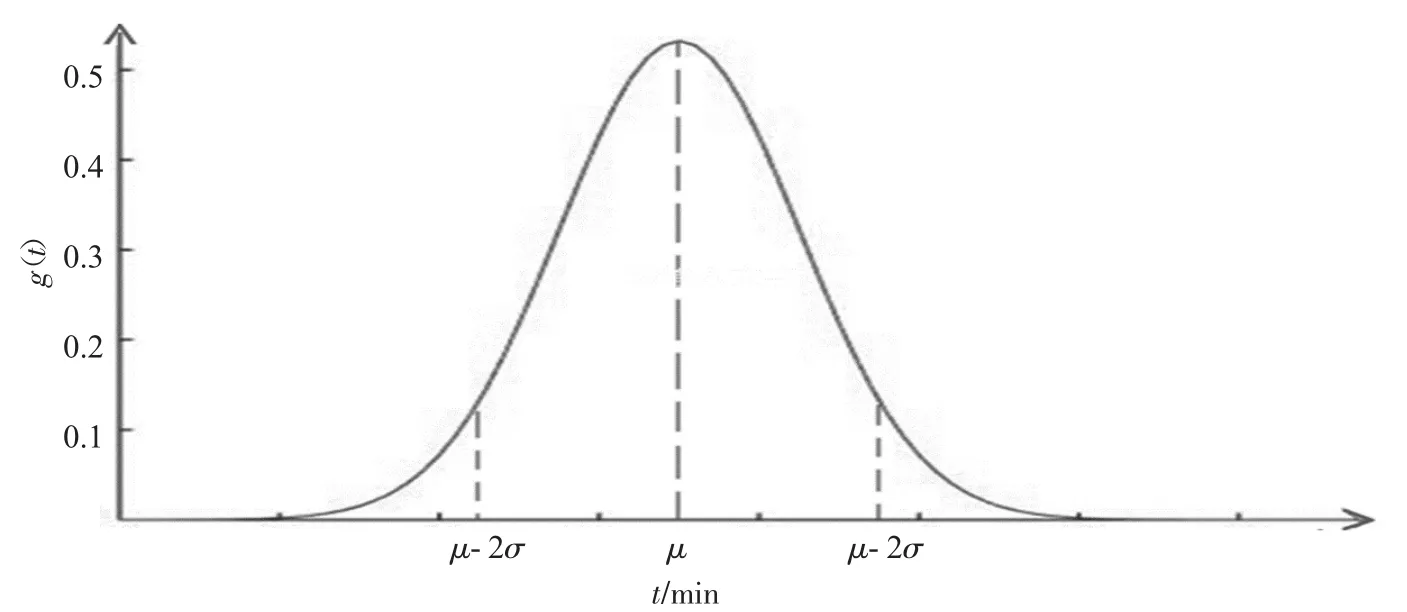
图5 到达目的地的时间概率分布图

图 5中

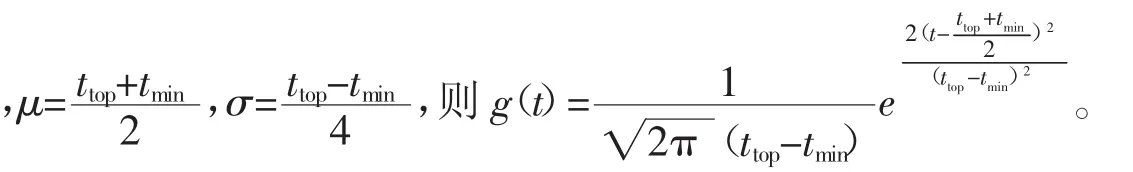
得到综合满意度模型为

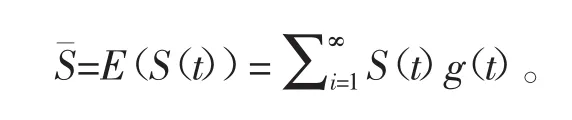
随机地以2017年2月16日上午11时深圳罗湖口岸的某位乘客为例，使用滴滴软件下单，目的地是世界之窗，启动A*算法［9］，得到最佳行驶路径上的路程为S=18.9 km，红绿灯个数为N=8，深圳白天的出租车平均驾驶速度为=0.7 km/min，在滴滴打车公司的协助下，获得了以R=2 km为研究半径下，该乘客对应的在线出租车供给量为15辆，接下该单的司机对应的乘客下单量为30单，供求比调节的车费为4.5元，初始价格为4元/min。当恒速下所对应的最小车费为元，最佳路径上等待红灯的最佳时长为2.67 min，最长等待红绿灯时长为8.53 min，恒速下的最佳驾驶时长为最长驾驶时长为当驾驶时长超过29.53 min时，单价将以ω=0.5元/min的速度下降，因此，所对应的最大车费为

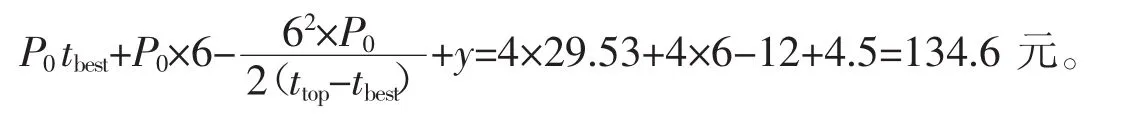
正态分布函数

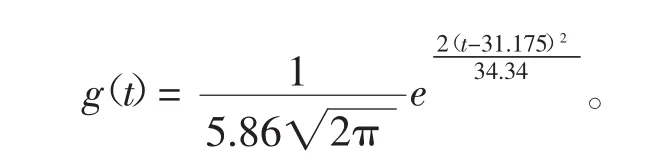
收入P与驾驶时间t的关系为

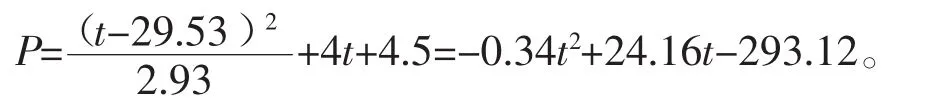
则司机满意度为Sd=-0.03t+2.06，乘客满意度为Sp=-0.058t+2.56，综合满意度函数为:S=83.86%。

为了更好地体现本文模型动态定价的高效性和高灵敏性，采用同一单固定价格得到的综合满意度进行对比，本示例中的固定单价为4元/min。

通过对比动态定价模型与固定价格模式下的打车方式，显然本文的动态定价模型具有更高的综合满意度，如表1所示。

表1 综合满意度对比表

此外，为了证明本文模型的实用可行性，随机调研不同区域下的打车实例进行验证，计算结果如表2所示。

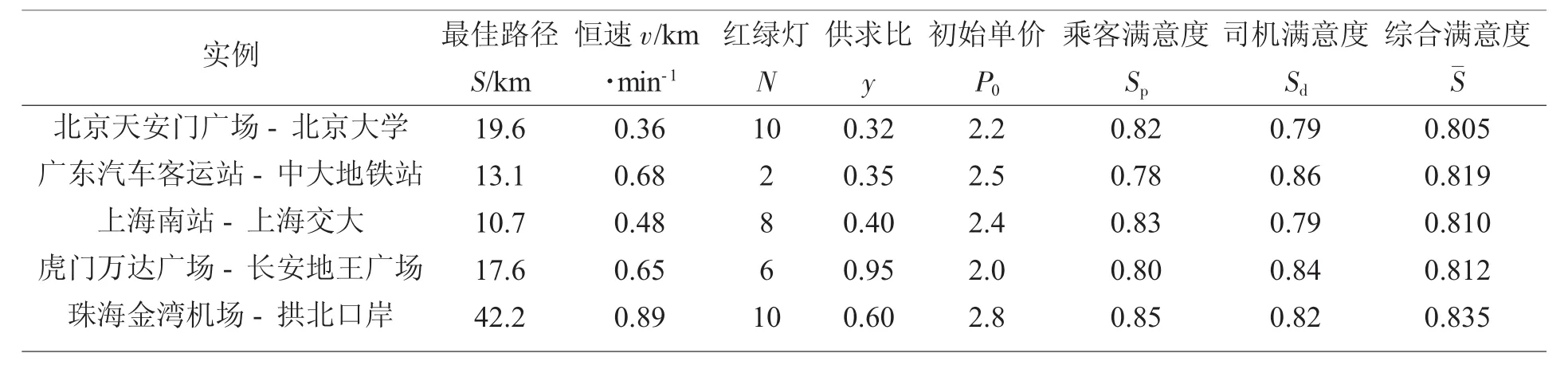
表2 实验验证结果

实验验证结果表明：本研究的动态定价算法具有高效性、高灵敏度。

5 结语

本文提出了一种新的出租车动态定价方法，该方法对出租车的动态定价明显优于传统的动态定价方法。考虑了最短路径上红绿灯对驾驶时间的影响，并通过实时供求比进行综合调节价格，既能够合理定价，又控制了调价峰值。验证结果表明，本定价算法充分考虑了司机和乘客双方的利益，同时也有效改善了司机“挑单”的现象，有助于从根本上缓解“打车难”问题。本文的定价方法优越之处是充分考虑了不同属性的订单以进行合理调价，适应性广，灵敏度高。

［1］杨芬娟.城市客运出租车定价问题的研究［D］.西安:西安交通大学,2012.

［2］胡骥,胡万欣,蒋晶尧.放松规制下的出租车服务定价博弈模型［J］.公路交通科技,2014,31（10）:148-153.

［3］张佳彤.打车软件参与下出租车动态定价策略研究［J］.唐山学院学报,2016,29（6）:78-84.

［4］李娟,靳文舟,裴明阳.“互联网+”时代下出租车运价结构优化调整研究［J］.公路与汽运,2016（3）:72-76.

［5］张文阁.北京市出租车交通需求预测及其应用研究［D］.北京:北京工业大学,2008.

［6］HALLJ,KENDRICKC,NOSKOC.The Effects ofUber’s Surge Pricing.［2015-09-17］.https://newsroom.uber.com/the-effects-of-ubers-surge-pricing/.

［7］戚蓓蓓,朱家明,秦欢,等.“互联网 +”时代的出租车资源配置［J］.交通企业管理,2015,30（12）:44-47.

［8］贾秀倩,刘翔.“互联网+”时代出租车资源“供求匹配”程度的合理性［J］.中国新通信,2016（2）:119-120.

［9］王云鹏,孙文财,李世武,等.基于ArcGIS的危险品城市运输路径优化模型［J］.吉林大学学报（工学版）,2009,39（1）:45-49.