图例化算法教学的探究与实践

摘要：随着信息技术课程的发展，计算思维已经成为信息技术核心素养四要素之一，如何培养学生具备一定的算法思维能力，已成为每一位信息技术教师面对的课题。笔者依托图例化教学方式，巧妙搭建了问题分析与程序代码之间的桥梁，培养学生构建算法思维的能力，落实了计算思维的培养与提高。

关键词：核心素养；计算思维；图例化；算法思维

普通高中信息技术学科的核心素养概括为信息意識、计算思维、数字化学习与创新、信息社会责任四个要素，其中计算思维是指个体运用计算机科学领域的思想方法，在形成解决问题方案的过程中产生的一系列思维活动。本人尝试以图例化分析为依托，编制适合计算思维培养的学案，培育思维构建方法，有效地培养了学生的计算思维能力。

一、 现状分析：忽视计算思维的算法教与学

算法问题的解决是由问题分析、思维构建、程序实现三部分组成的，这一过程中算法思维构建是关键。然而在实际教学活动中，教师由于缺乏有效的思维构建方式，而不自觉地将算法思维构建简单化；学生会忽视算法思维对程序理解的重要作用，反而把机械的读程序作为理解和学习算法的途径。于是便会出现教师无论怎么教也无法让学生理解算法，学生不管怎么努力也找不到有效的算法学习方式的怪圈。

因此，本人设计了图例教学法，来帮助教师开展有效的算法思维教学，帮助学生形成高效的算法思维方式。

二、 探究与实践：“展，推，解”，图例化算法教学实践

图例教学法可以灵活运用于新课讲授、思维构建与难题解决等情况，分别采用“展、推、解”三种不同手段，来解决算法学习、问题分析和难题解题上碰到的不同问题。

（一） 展：循序渐进，图例展知识要点

高中算法教学中需要学生掌握解析算法、枚举算法、排序算法（冒泡排序和选择排序）、查找算法（顺序查找和对分查找）、递归算法等基础算法。

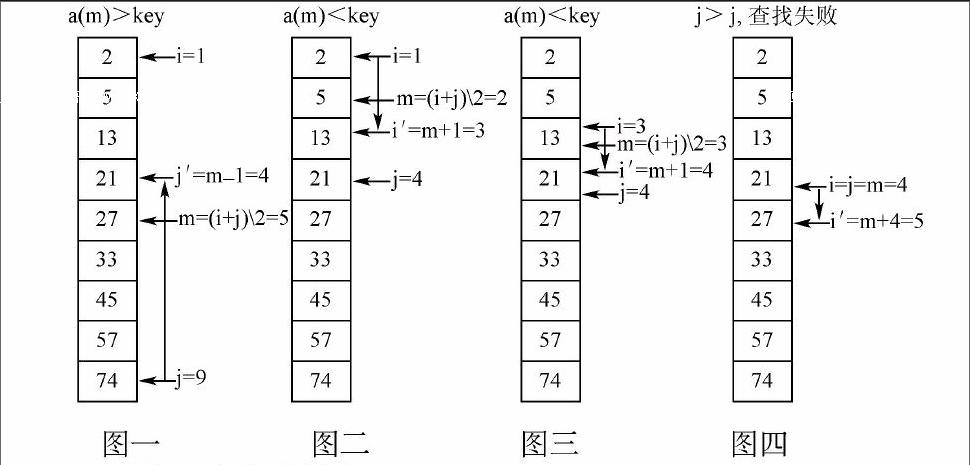
例如对分查找算法，我们可以将数组中的数据假想成一列连续的数据块，而上标i、下标j和查找位置m的变化可以设计成由“←”和伪代码组成的符号来演示：

以查找键值key=25为例

算法思想总结如下：

1. 图1中，出现了a（m）>key，下标j移动到m-1的位置上：若a（m）>key，则j=m-1。

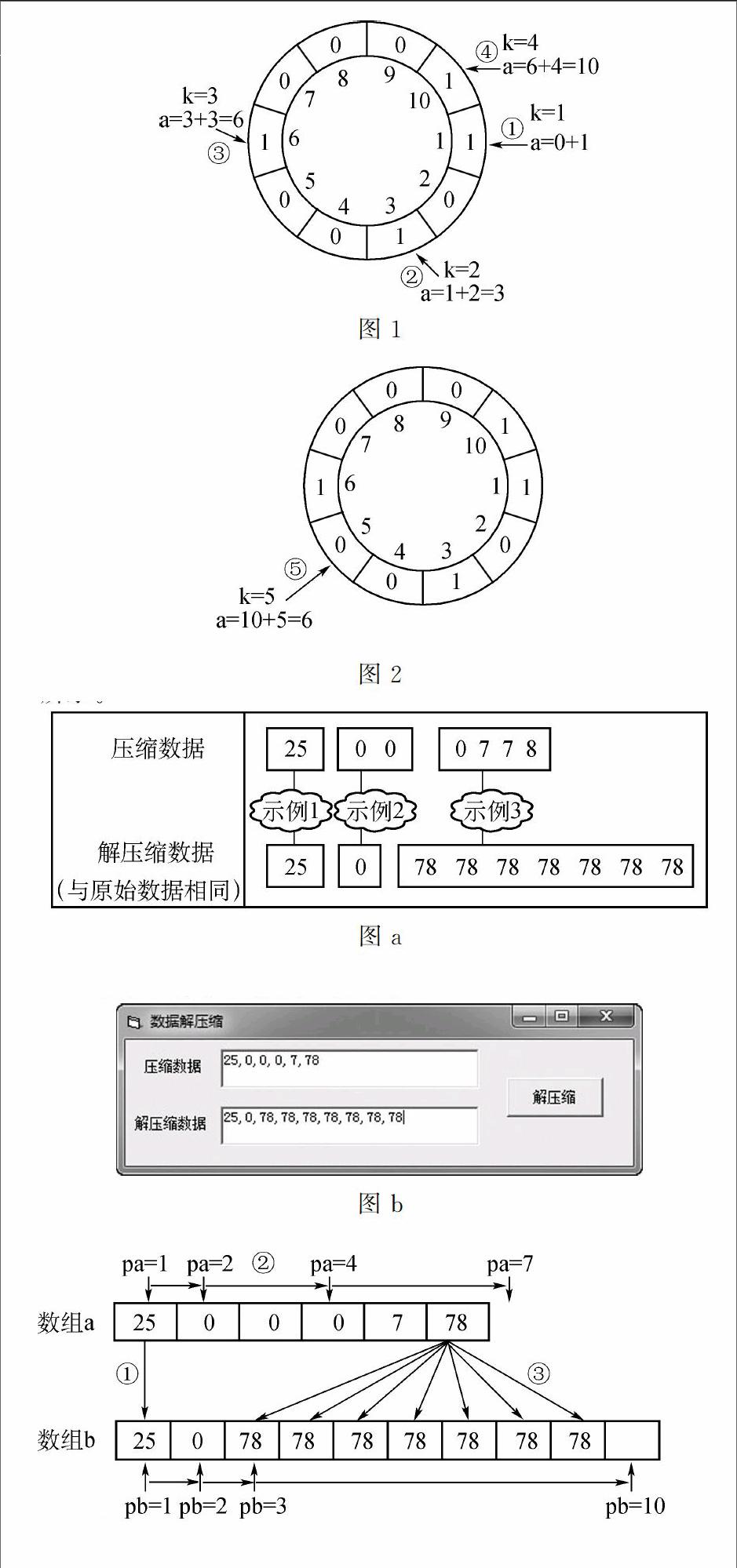
2. 图2中，出现了a（m）

3. 图3的情况与图2相同，但是不能将此图去掉，因为它展示了对分查找算法是一个按照固定规律重复执行的算法：对分算法是一个循环算法。

4. 图4中，我们可以明显地看到，上标的i已经移动到下标j的下面，此时算法结束：采用“Do While i<=j”的结构来实现对分查找。

图例的演示和总结，还能帮助学生理解程序设计中相应的代码。

伪代码与图例的关系如下：

i=∶j=n

Do While i<=j由图4归纳而来

m=（i+j）＼＼2图1，图2中表示

IF a（m）=key ThenExit do归纳得来

IF a（m）>key Thenj=m-1Else i=m+1图1，图2中归纳得来

Loop

IF i>j Then查找失败Else输出查找结果'从图4中推论得出

学生通过图例的演算推导，不仅理解了对分查找的思维过程，理解了标准对分查找程序代码中各段代码的作用，而且对于对分查找结束后结果判断表达式的理解也起到了很重要的作用。

（二） 推：情景再现，图例推思维过程

实际情景类的算法的问题往往以实际问题为背景，此时的算法是根据实际问题分析得到的，这类算法问题才是日常程序设计中真正解决的问题，也是我们在教学中要培养的计算思维的精髓所在。

如题：【摘自金华一中《信息技术选考全案导学》】

经典的狐狸抓兔子故事：围绕着山顶有10个洞，狐狸要吃兔子，兔子说：“可以，但必须找到我，我就藏身于这下个洞中，你从10号洞出发，先到1号洞找，第二次隔1个洞找（即3号洞），第三次隔2个洞找（即第6号洞），以后如此类推，次数不限。”但狐狸从早到晚进进出出了1000次，仍没有找到兔子。问兔子究竟藏在哪个洞里？

实现上述功能的程序如下，但加框处代码有误，请改正。

Private Sub Command1_Click（）Const n = 10Dim hole（10） As Integer

Dim i，j，number As IntegerFor i=1 To 10hole（i）=0

Next inumber=0For j=1 To 1000

number=number+1（1）应改为

i=number Mod n

If i=0 Theni=1（2）应改为

hole（i）=1

Next jFor i=1 To nIf hole（i）=0 Then

List1. AddItem“兔子可能藏在”& Str（i） &“号洞”End IfNext iEnd Sub

笔者采用图例化方式再现狐狸寻找的过程，帮助学生理清思路，找到突破口。

图例设计分析：

1. 由于这10个洞不是线性排列的，而是成环形的，因此图例表示时采用环形来表达各个洞的排列。

2. 狐狸寻找时洞穴号是一个变化的数字，且有一定的规律。

由此得到如下所示的图例：

问题解决：

“（1）”处代码原为“number=number+1”，通过上面的分析可知number=上一次的洞穴数+第几次找洞穴且变量j代表了现在是第几次找洞穴。

故应当改为“number=number+j”。

“（2）”处代码原为“if i=0 Then i=1”，从图1可以看到当寻找洞穴号为10的时候（即number=10）时，变量i会计算出0，而此时需要寻找的洞穴是10号。

故应当改为“If i=0 Then i=n”或“If i=0 Then i=10”。

我們利用图例将狐狸寻找兔子的过程再现，即理解了算法设计的思维过程，也通过图例总结出了算法设计的关键点，再来解决程序代码改错也就水到渠成了。

（三） 解：抽丝剥茧，图例解难题要点

有不少算法虽然给出了具体的算法过程，但是将这一过程转化为程序代码后，难免会有一些设计上的变化，如果学生能够在阅读程序过程中辅以图例演算，那么就能够在难题解决上找到突破口。

如题：【摘自2016年4月浙江省高中学业水平统一考试】

某数据压缩方法描述如下：

1）原始数据中，某数不为0且相邻无重复，压缩数据用该数据表示；2）原始数据中，某数为0且相邻无重复，压缩数据用两个数表示，第1个位0，第2个位0；3）原始数据中，某数据相邻有重复，压缩数据用3个数表示：第1个位0，第2个为重复数的个数，第3个为该数本身；

根据上述压缩方法，对应的解压缩方法示例如图a所示。

程序运行界面如图b所示。

部分代码如下：

pa=1∶pb=1Do While pa<=nfirstdata=a（pa）

If firstdata<>0 Then示例1情况处理b（pb）=firstdata

pa=pa+1∶pb=pb+1

Elsecount=a（pa+1）If count=0 Then示例2情况处理

b（pb）=0pa=①∶pb=pb+1Else示例3情况处理

Fori=1 To count②

Next ipa=pa+3∶pb=pb+count

End If

End If

Loop

Text2. Text=Str（b（1））For i=2 To ③

Text2. Text=Text2.Text+，+Str（b（i））

Next i

由于本题中涉及两个不同的数组，且数组之间有数据的赋值，我们可以设计上下两个图例来演示它们的数据交换过程，并用题目中所给的数据为演算数据。结合部分程序代码，我们可以用图例还原两个数组之间数据交换的全部过程。

问题解决：

“①”处代码为示例2情况下将数组b赋值完后，两个数组指针pa和pb的移动，从图中可以看到对于示例2需要数组a中出现两个连续的0，因此处理完成后要跳过这两个0。故答案为：pa=pa+2

“②”处代码为示例3情况下将数组a中从pa出发第3个元素的值赋值到数组b中，且要放在count个元素中。故答案为：b（pb+i-1）=a（pa+3）

“③”处代码为最后输出数组b中的内容，从图中可以看出指示数组位置的指针pb在每一次完成处理后，肯定会移动到下一次处理的开始位置，因此最后统计数组b中有多少元素时只需要将pb-1就可以得到。故答案为：pb-1

该题的算法演变过程非常的精准，两个指针pa和pb的移动也非常的讲究。我们通过图例的方式，完美地将算法思想与程序代码结合，即分析了算法中的变化过程，也让学生很容易地理解了算法的代码，从而顺利地解决了题目中的难点。

图例化教学的核心在于过程的展示、思维的推理和模型的解释，科学合理地运用图例来解释算法、构建思路和重现过程，能够有效地帮助学生理解算法的精要。运用图例教学法遵循了从感性到理性的演变，从感性的图例来推导出理性的代码，更重要的是在问题分析过程中让学生体会到了算法设计的真实思路与思维方式。这是一种能力上的锻炼与提高，也为我们培养学生的计算思维起到了至关重要的作用。

参考文献：

[1]普通高中信息技术课程标准（征求意见稿）[S]，2016.

[2]陶增乐等.算法与程序设计[M].浙江教育出版社，2005.

作者简介：张霖，浙江省义乌市，义乌市第四中学。endprint