基于耦合偏微分方程的SAS图像相干斑抑制方法∗

黄 攀 唐劲松 徐 魁 钟何平

（海军工程大学海军水声技术研究所 武汉 430033）

1 引言

合成孔径声纳（Synthetic Aperture Sonar：SAS）是一种新型的高分辨率水下成像声纳，由于其高分辨率特点，被广泛应用于水下小目标搜索、航道测绘、水下战场精细测绘与侦察、海洋湖泊河流地形/地貌测绘等［1～4］。相干斑噪声是在回波信号中产生的，是SAS系统所固有的，它不同于数字图像处理中的噪声。相干斑噪声的存在给图像带来很多不利，它降低了图像的质量，使图像难以分析和理解、不利于目标的识别与检测，因此需要对相干斑噪声进行去除。目前关于SAS图像相干斑抑制算法研究比较少，主要是借鉴的合成孔径雷达中的相干斑抑制方法。SAS相干斑抑制要求既要去除噪声，又要尽量地保持边缘细节信息。常用的相干斑抑制方法有局部统计自适应方法［6～7］、小波方法［8］和偏微分方程方法（partial differential equation，PDE）［9～10］。在统计自适应方法中，Lee滤波算法［5］是一种有效的SAS图像相干斑算法。PDE方法中最为经典的是P-M模型［11］，但是P-M模型是不适定的［12］，因此Catte等［13］提出了正则化的P-M模型，其中要用到高斯预滤波，正则化P-M模型的缺点是高斯预滤波是各向同性的，对各个方向上的滤波能力相同，这样就会损失一些有用的细节信息，而且高斯函数的方差的选择需要人为的预先设定，对于不同的图像要选择不同的方差。

本文针对正则化P-M滤波模型的上述缺点，提出了一种耦合的PDE滤波方法。该方法中引入了边缘强度函数，用以控制滤波过程中边缘的保持。并且在新方法中引入对流项，用来控制扩散的方向，这样更有利于保持边缘细节信息。最后通过实际的SAS图像处理实验，将本文方法的结果和传统的正则化P-M方法结果和经典的Lee滤波结果作比较，验证了该方法在去噪能力和边缘保持能力上的优势。

2 传统滤波算法

2.1 Lee滤波

Lee滤波是利用图像局部统计特性进行SAS图像相干斑抑制的典型方法之一，它是基于完全发育的乘性噪声模型，假设噪声模型如下

其中R是含噪声的观测图像，s是没有噪声的图像，n为相干斑噪声。s和n是相互独立的，且噪声的均值为1，即nˉ=E[n]=1。假定s的先验均值和方差可由图像的局域均值和方差估计得到。s的先验均值为 sˉ=Rˉ/nˉ=Rˉ，s的方差为

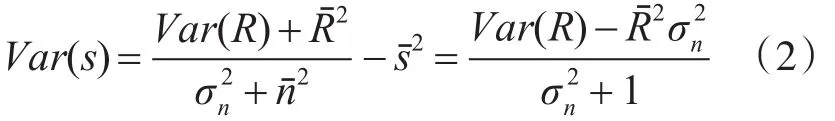
其中Var(R)和Rˉ分别为含噪声图像的方差和局部均值，σn为噪声标准差。经过Lee滤波算法进行相干斑噪声抑制后的图像可以表示为

其中

2.2 正则化P-M滤波模型

PDE滤波方法中最经典的是P-M模型，它是由Perona和Malik［11］提出，表达式为

式中，u0是滤波前的图像，u(x，y，0)表示滤波的初值（即0时刻的值），(x，y)是空间位置。∇是梯度算子是梯度模值，∇·()是散度算子。式（4）中第一个式子是扩散方程，其中g(||∇u)是扩散系数函数，它控制着扩散速度。这里选择的扩散系数函数g(s)的表达式为

式中K为阈值。

由于扩散系数g(| ∇ u|)的大小依赖于图像的梯度模值 | ∇u|，在图像梯度模值 | ∇u|较小的区域，即变化缓慢的平坦区域，扩散系数g(| ∇ u|)比较大，平滑作用就较强，滤波越明显。而在图像梯度模值|∇u|较大的区域，表示图像变化较快，此时扩散系数g(| ∇ u|)就变小，平滑作用就降低，滤波就不明显，特别是在图像的边缘，由于 | ∇u|足够大，g(| ∇ u|)几乎为0，因而扩散几乎停止，从而达到保持边缘的目的。

但是P-M方程的解是不适定的［12］，因此，Catte等［13］提出了正则化的P-M模型，其表达式为

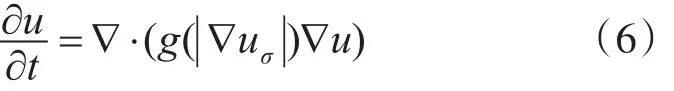
初值条件依然和P-M模型相同，只是将P-M模型中的扩散系数函数中的u改成了uσ。其中uσ=Gσ*u，这里

uσ的物理意义就是用方差为σ的高斯函数与原始图像做卷积运算，即进行高斯低通滤波的预处理，目的是将一小部分噪声去除，以减少将噪声当成伪边缘的可能性。数学上已经证明，式（6）是完全适定的［13］。

3 耦合PDE滤波算法

在正则化P-M模型中要经过高斯预滤波，高斯预滤波的本质是一个以高斯模板进行线性滤波的过程，虽然高斯预滤波过程可以去除很多噪声，为后续的PDE滤波带来很大帮助，但是由于高斯预滤波在各个方向上滤波作用是一样的，就会损失一些有用的细节信息，而且高斯函数的方差的选择需要人为的预先设定，对于不同的图像要选择不同的方差。因此本文提出了基于耦合偏微分方程的相干斑滤波方法，克服了高斯预滤波的缺陷，耦合PDE方程模型为

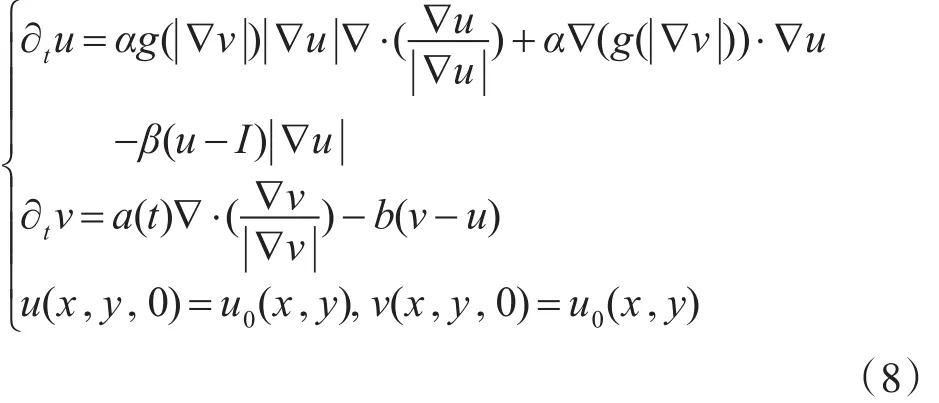
在这个模型中，引入了边缘强度函数v，它在滤波过程中起着重要作用，用以保持边缘信息。其中 g( ||∇v)=1(1+ ||∇v2K2)，它控制着扩散速度。I是原始含噪声图像，式（8）中第一个方程等式右边第一项为扩散项，第二项为对流项，第三项为保真项，即保证滤波后的图像u和原始图像I不会相差太大。系数α，β的作用是使右端三项的影响折衷。a(t)是随着时间变化的参数，b是常数。a(t)随着时间增加而减小，可以有效地增加u与v的一致性。

耦合PDE模型的具体求解过程如下：

1）为u，v设定初值，初值都为原始图像；

2）通过式（8）的第二个方程求出v；

3）计算扩散系数函数g( ||∇v)的值；

4）通过式（8）的第一个方程求u；

5）完成一次迭代，再进行下一次迭代。

式（8）中具体的离散化数值求解方法参见文献［14］。

4 实验结果分析

图1 各种滤波方法比较

为了验证本文所提方法的有效性，将本文方法与正则化P-M方法和经典的Lee滤波方法相比较。试验数据选用一幅合成孔径声纳样机试验所得成像结果数据，如图1（a）所示。经过5×5窗口的Lee滤波结果如图1（b）所示，正则化P-M滤波选择参数为∆t=3，K=10，循环次数N=2，其结果如图1（c）所示，本文的耦合PDE滤波方法选取参数为α=0.5，β=0.0005，b=0.1，∆t=0.3，a()0=1，迭代次数N=20，滤波后的结果如图1（d）所示。

比较图1中的（b）～（d），可以发现，图1（b）和图1（c）都出现了过度滤波的现象，从图的幅度上就能看出这一点。另外，在图像的边缘，例如图的左下角的凹坑的边缘，图1（b）和图1（c）的边缘比较模糊，不如图1（d）保持的好。

为了定量的评价三种方法的质量，本文选择了等效视数（ENL），边缘保持指数和图像方差作为评价标准。等效视数是衡量一幅图像相干斑噪声相对强度的一种指标，ENL越大说明图像上的相干斑越弱，图像质量越高，等效视数的定义如下：

式中μR和σR分别是图像的均值和标准差。

边缘保持（ESI）是指保持图像的边缘信息，即去斑处理后的图像边缘不模糊，边缘点位置不移动。边缘保持指数ESI可以有效地表征滤波处理后对图像边缘的保持能力。其定义为

其中Ih，Il分别是去噪后的图像边缘像素的灰度值，Iˉh，Iˉl是去噪前的边缘像素的灰度值。 m 是沿着边界的像素个数。ESI越大，说明边缘保持能力越好。

三种方法的定量评价结果如表1所示。从表1中的各项指标可以看出，Lee滤波的ENL和ESI都是最低的，说明它的滤波去除能力和边缘保持能力都不如偏微分方程滤波方法好。本文的耦合的PDE方法的ENL和ESI比正则化P-M方法稍微高一些，说明本文所提方法在保持边缘和去除噪声能力上都比传统的偏微分方程方法强。

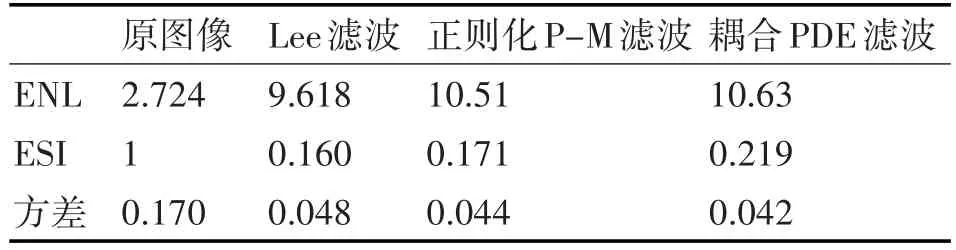
表1 各种相干斑抑制方法处理结果比较

5 结语

本文提出了基于耦合偏微分方程的合成孔径声纳图像相干斑抑制方法。该方法引入了边缘强度函数，用来保证滤波过程中边缘不被过度滤波，克服了传统的偏微分方程正则化P-M模型中高斯预滤波在各个方向上滤波效果相同的缺点。通过实际的SAS图像数据处理实验，结合等效视数，边缘保持指数和方差三种指标，将本文方法的结果与传统的正则化P-M方法和经典的Lee滤波方法结果进行比较，验证了本文的耦合PDE方法在去噪能力和边缘保持上的优势。

［1］佟宏伟，钟何平，唐劲松，吴浩然.基于GPU的SAS成像算法并行实现研究［J］. 舰船电子工程，2014，34（3）：137-140.

［2］Hayes P M，Gough T P.Synthetic Aperture Sonar：A Re⁃view of Current SASStatus［J］.IEEE Journal of Oceanic Engineering，2009，34（3）：207-224.4，34（3）：137-140.

［3］赵永祯，唐劲松，钟何平.基于声纳图像纹理特征的海底底质分类方法研究［J］. 海洋测绘，2015，35（3）：60-63.

［4］钟何平，唐劲松，张森，等.基于图形处理器的合成孔径声纳实时距离多普勒成像算法［J］.电子与信息学报，2014，36（8）：1899-1904.

［5］Lee JS.Speckle suppression and analysis for synthetic ap⁃erture radar images［J］.Optical Engineering，1986，25（5）：636-642.

［6］Kuan D T，Sawchuk A A，Strand T C et al.Adaptive noise smoothing filter for images with signal-dependent noise［J］.IEEETrans.Pattern Analysis and Machine Intel⁃ligence，1985，7（2）：793-802.

［7］Frost V S，Stiles JA，Shanmugan K Set al.A model for radar images and its application to adaptive digital filter⁃ing of multiplicative noise［J］.IEEE Trans.Pattern Analy⁃sis and Machine Intelligence，1982，PAMI-4：157-166.

［8］Bhuiyanr M，Ahmad M，and Swamy M.Spatially adaptive wavelet-based method using the cauchy prior for denois⁃ing the SAR images［J］.IEEE Transactions on Geosci⁃ence and Remote Sensing，2007，17（4）：500-507.

［9］Yu Y and Acton S.Speckle reducing anisotropic diffusion［J］.IEEE Transactions on Image Processing，2002，11（11）：1260-1270.

［10］黄攀，岳军，陈鸣，王茂林.基于偏微分方程的InSAS干涉图去噪技术研究［J］.青岛理工大学学报，2011，32（6）：104-106.

［11］Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion［J］.IEEE TPAMI，1990，12：629-639.

［12］Yu-Li You，Wenyuan Xu，Allen Tannenbaum et al.Be⁃havioral Analysis of Anisotropic Diffusion in Image Pro⁃cessing［J］.IEEE Transactions on Image Processing.1996，Vol 5，No 11，1539-1553.

［13］Catte F，Coll T，Lions P L，Morel J M.Image selective smoothing and edge detection by nonlinear diffusion［J］.SIAM J.Numer.Anal，1992，29：182-193

［14］ L.Rudin，S.Osher，E.Fatemi.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60：259-268.