带钢纠偏系统的自抗扰控制

张东洋，姚小兰，焦路亮

(北京理工大学 自动化学院，北京 100081)

纠偏控制系统广泛应用于金属带材(如带钢、带铝等)轧机、纵剪机列和清洗机列等生产中，是带材处理线上重要的环节。其作用是对齐带钢的边部或者使其运行在轧制线中央，从而保证带钢轧制产品的质量。

典型的带钢纠偏控制系统主要由光电传感器、控制器、伺服系统和纠偏辊组成。当系统正常运行时，带钢处于光电传感器中央，如果带钢跑偏，即偏离光电传感器中央，则由光电传感器检测出带材的位置偏差，并将信号传输到电控装置，经过放大等一系列的作用后传输到伺服控制系统，伺服系统推动液压缸以驱动纠偏辊来调整带钢的位置。带钢位置由光电传感器进行位置跟踪，当跟踪位置与设定值相等时，偏差信号为零，处于新的平衡，从而实现带钢纠偏。

纠偏控制系统始于20世纪60年代末期，在80年代和90年代有了很大的提高[1]。近年来，由于结构简单以及参数整定方便，工业生产线中常采用传统的PI/PID控制，但传统的PI/PID控制很难满足高精度和快速性的要求。为了进一步提高系统的控制性能，研究者们又提出了智能控制、模糊PID控制和滑模变结构控制等方法[2-3]。在纠偏控制系统回路中(包括位置环和速度环)，位置环对扰动以及闭环控制系统的稳定性起主要作用，然而，目前存在的控制方法对系统扰动抑制能力很弱，从而影响了整个控制系统的性能，限制了这些现存方法的实用性；因此，寻找一种有效的控制策略实现高精度、快速、有效的纠偏控制很有必要。

自抗扰控制(ADRC)技术的出现，给带钢纠偏控制带来一种新的思路[4-5]。自抗扰控制技术能够实时估计并补偿系统内部动态扰动和外部扰动，是一种响应速度快、算法简单、精度高、适用范围广、抗干扰性强且不依赖于系统的模型的新型反馈线性化控制策略，理论上更适用于以抗干扰为主要任务的纠偏系统。基于此，本文采用自抗扰控制实现了高精度、高抗扰性的带钢纠偏系统的控制，并对该控制器的稳定性进行证明，总结出基于带宽法的参数整定方法，并将自抗扰控制器应用到带钢纠偏系统仿真模型中，与工业PI控制器在跟踪和抗干扰性能上进行了比较分析，以验证该控制器设计方法的有效性。

1 带钢处理线偏差校正系统模型

在带钢高速运行过程中，一些外部因素(如速度、张力和温度)的变化会引起带钢位置偏差，甚至发生断带现象，带钢纠偏控制系统主要就是针对带钢位置与设定值之间的偏差进行纠正，使带钢运行在中心位置。中心位置控制(Central Position Control，CPC)的稳定性和抗干扰能力是实现带钢稳定纠偏控制的前提，因此，为了实现带钢的稳定控制，需要寻找一种有效的控制方法来隔离扰动的影响。

1.1 系统分析

带钢偏差的修正是通过调节纠偏辊的摆动来实现的。由于电液伺服控制性能(输出功率大和动态响应时间短)优于电伺服控制，因此，本文选择电液伺服系统。文献[6]已经将电液伺服控制系统应用于带钢纠偏控制系统中，控制框图如图1所示。

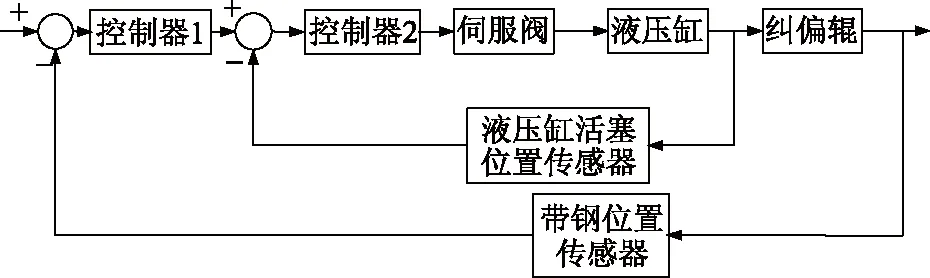
图1 纠偏控制系统结构框图

1.2 纠偏系统模型

1.2.1 液压缸模型

本文研究的纠偏系统的液压缸是一个伺服阀控制的单杆液压缸。模型的建立包括液压伺服阀的流量方程、液压缸流量的连续性方程以及液压缸与负载之间的力平衡方程[7]。

本文做如下假设：液压油源恒压；液压伺服阀为零开启精确定心阀；忽略泄漏和泄漏对系统的影响。

1)液压伺服阀的流量方程。方程为：

qL=kqxv-kcpL

(1)

式中，qL是负载流量；kq是流量增益；xv是阀门开度；kc是流量压力系数；pL是负载压力。

2)液压缸流量的连续性方程。方程为：

(2)

式中，Ap是液压缸活塞的有效面积；xp是活塞位移；Vt是总压缩量；βe是有效体积弹性模量。

3)液压缸与负载之间的力平衡方程。方程为：

(3)

式中，mt是加到活塞上的总质量；Bp是活塞和负载的粘滞阻尼系数；K是负载弹性刚度，FL是作用于活塞的负载流量。

对上述三部分模型进行拉氏变换，得出：

(4)

由式4可以推导出液压缸的传递函数为：

(5)

除去弹性负载，忽略负载的扰动，式5可以写成

(6)

在电液伺服系统中，xv不能直接测量，可由无负载流量间接表示为：

Q0=Kqxv

(7)

因此，液压缸的传递函数为：

(8)

(9)

且需保证液压缸的频率：

(10)

1.2.2 电液伺服阀模型

本文研究的系统采用三位四通阀，电液伺服阀的固有频率是23 Hz，液压系统的固有频率是24 Hz。当电液伺服阀的固有频率与液压系统的固有频率接近时，电液伺服阀可以近似为1个二阶振荡连杆[8]，其传递函数为：

(11)

式中，Ksv是伺服阀的流量增益；ωsv是伺服阀固有频率；ζsv是伺服阀的阻尼系数；Q0(s)是伺服阀的空载流量；I(s)是伺服阀的额定电流。

(12)

式11的频域特性为：

(13)

式12的频域特性为：

(14)

由伺服阀的额定流量Q(s)=6.67×10-4m3/s，伺服阀的额定电流I(s)=0.3 A，燃油压力Ps=9 MPa，额定压降Pn=7 MPa，可得：

(15)

根据纠偏系统的工作情况，查阅所选伺服阀参数可知：ζsv=0.7，ωsv=144，代入式12，可得：

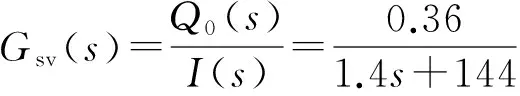
(16)

1.2.3 传感器模型

1)带钢位置传感器。带钢位置传感器的范围为0～500 mm，输出电压为-10～10 V。带钢位置传感器可以看成是一个比例环节，则其模型为：

(17)

2)液压缸活塞位移传感器。由于位移传感器的固有频率远远高于系统中元件的固有频率，所以把位移传感器近似看成比例环节。Lw为液压缸活塞的有效行程，Lw=500 mm，和带钢位置传感器范围一致；位移传感器的输出电压为-10～10 V，用Iw表示。则液压缸活塞位移传感器模型为：

(18)

1.2.4 纠偏辊模型

由于比例积分效应纠偏辊应用广泛，本文将其作为实例来分析纠偏辊模型的传递函数。查阅相关文献，比例积分效应纠偏辊有最大旋转角度，取为5°。如上所述，液压缸活塞杠的有效行程为500 mm。将液压缸活塞位移和纠偏辊的旋转角度近似看作一个比例环节，则：

(19)

在这里，选取积分效应纠偏辊为例，带钢偏差可以简化为：

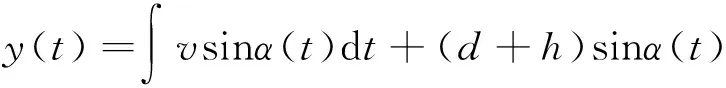
(20)

由于偏差角很小，且sinα≈α，则：

(21)

对式21求导并进行拉氏变换，得到：

(22)

式中，v=150 m/min；d=0.1 m；h=1 m。由式19和式22可得，纠偏辊的传递函数为：

(23)

综上所述，结合每部分模型的传递函数得到带钢纠偏系统控制结构框图如图2所示。

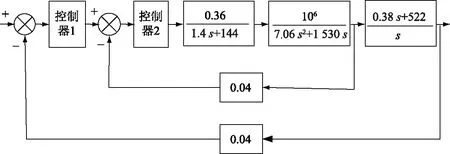
图2 带钢纠偏系统控制结构框图

2 控制系统设计

结合式9和式12，可以得到：

(24)

由于典型I型系统的超调性能优于典型II型系统，但其抗扰性弱，所以，内环采用I型控制器，即PID控制策略，传递函数为：

WPD(s)=K2p(1+τds)

(25)

取微分时间常数τd=2ζh/ωh，则内环闭环传递函数为：

(26)

外环(位置环)采用抗扰性强的自抗扰控制器，这样既实现了小超调量，又达到了抗扰性的目的。

2.1 自抗扰控制器结构

典型的自抗扰控制器组成包括1个跟踪微分器(TD)、1个扩张状态观测器(ESO)、状态误差反馈(SEF)和扰动补偿项。在实际应用中，不需要TD环节，且为了减少控制器参数，常采用线性自抗扰控制结构，即线性状态误差反馈(LSEF)和线性扩张状态观测器(LESO)。

根据传递函数(式26)，设计1个二阶线性自抗扰控制器，控制器结构如图3所示。

图3 闭环系统结构图

将被控对象(式26)转化成如下形式：

(27)

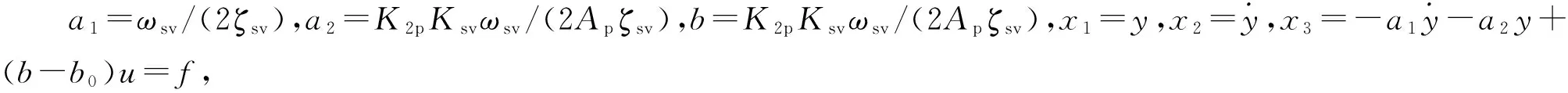
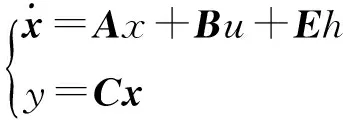
(28)

对于式28，按照自抗扰控制的设计方法，利用扩张状态观测器用于系统状态和总扰动的估计，其结构为：

(29)

式中，β1,β2,β3为需要确定的扩张状态观测器参数。

状态误差反馈控制律为：

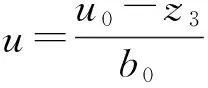
(30)

式中，kp、kd、b0为控制器参数；r为参考输入。

2.2 自抗扰控制器稳定性分析

稳定性是控制系统应用的最基本条件之一，针对自抗扰控制器的稳定性目前也有很多研究[9-13]。本文将针对二阶线性自抗扰控制器进行稳定性分析。

结合式28和式29，可以得到观测器误差为：

(31)

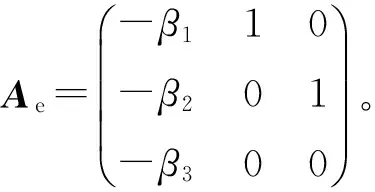
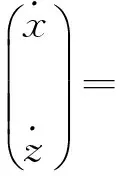
(32)

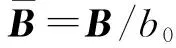
很明显，闭环系统是有界输入有界输出(BIBO)稳定的，如果式32的特征值都具有负实部，则闭环系统的特征值满足：

(33)

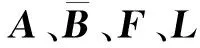
(34)

也就是说，闭环系统的稳定性是由式34所示的特征多项式决定的。为了便于分析，令：

(35)

可见，扩张状态观测器和自抗扰控制闭环系统的稳定性是由带宽ω0和ωc决定的。根据项z3/b0可以得出，控制增益b0能够补偿系统扰动项，且大量研究表明，闭环系统稳定域将会随着b0的增大而增大。

2.3 参数整定方法

由式33可以看出，观测器带宽ω0、控制器带宽ωc以及控制增益b0需要整定。

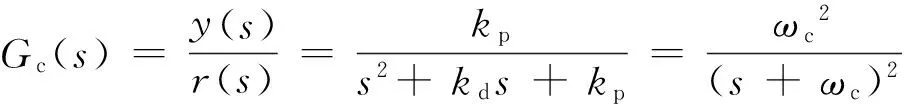
(36)

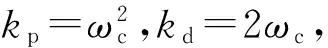
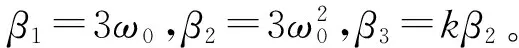
综上得出该二阶控制器的参数整定过程为：1)给定ts，令k=4，根据式37，确定kp、kd；2)根据式38，计算β1、β2、β3；3)反复调节b0，直至满足系统要求，结束。

3 仿真实例分析

为了验证本文设计的控制系统的有效性，下述将从跟踪性能和抗扰性能方面进行仿真分析。仿真参数见表1。

表1 PID与ADRC仿真参数

3.1 跟踪性能

当不加入任何扰动时，设定值为400，跟踪性能如图4所示。从图4中可以明显看出，本文提出的控制系统的跟踪性能优于PID控制方法。具体的性能比较见表2。

表2 PID与ADRC控制跟踪性能比较

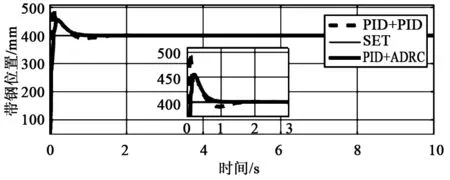
图4 闭环系统跟踪性能

3.2 抗扰性能

当t=5 s时，增加1个控制输入扰动u1=10时，闭环系统的响应如图5所示。当增加1个正弦扰动时，闭环系统的响应如图6所示。从图5和图6可以看出，自抗扰控制方案的抗扰性优于PID控制。图5中，当加入1个控制输入扰动时，需要大约0.4 s恢复到稳定状态，且超调量很小；而PID控制方法需要1.3 s恢复到原稳定状态，且超调量很大。图6中，当加入正弦扰动时，自抗扰控制方案以很小的误差在稳定状态上下波动；而PID控制的振荡很明显。

图5 具有控制输入扰动的位置纠偏控制响应

图6 具有正弦扰动的位置纠偏控制响应

为了进一步验证自抗扰控制的抗扰性，加入1个白噪声扰动，闭环系统的响应如图7所示。从图7可以看出，自抗扰控制方案效果优于PID控制方法。

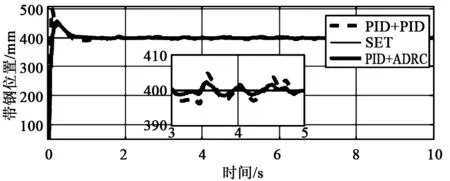
图7 具有白噪声扰动的位置纠偏控制响应

综上所述，本文提出的双闭环自抗扰控制方案能够有效地控制带钢纠偏系统，且性能优于传统的PID控制方案。

4 结语

本文主要针对带钢纠偏系统设计了双闭环自抗扰控制方案，用于实现带钢跑偏纠正。设计了1个二阶线性自抗扰控制器用于位置外环控制，内环采用PID控制；并证明了自抗扰控制闭环系统的稳定性，总结出了控制参数整定规则，提高了所设计控制方案的实用性；对带钢纠偏系统进行仿真分析，验证了自抗扰控制方案的有效性，且具有很强的抗扰性能。

[1] Zhang M Y, Yang H B, Zhang J B, et al. Servo system of harmonic drive electromechanical actuator using improved ADRC[J]. Optics & Precision Engineering, 2014, 22(1):99-108.

[2] Fan K, Yang Q, Yan W, et al. Fuzzy-PID based deviation-correcting control system for laser guided AGV[C]// Proceedings of International Conference on Modeling, Identification & Control. IEEE, 2012.

[3] Wang H, Bao Y. Fuzzy-PID dual mode fuzzy control of the electro-hydraulic deviation control system[C]// International Conference on Mechanic Automation and Control Engineering. IEEE, 2010.

[4] 韩京清. 自抗扰控制技术[M]. 北京：国防工业出版社, 2009.

[5] 黄一，薛文超. 自抗扰控制：思想，应用及理论分析[J]. 系统科学与数学, 2012, 32(10):1287-1307.

[6] Elbayomy K M. PID controller optimization by GA and its performances on the electro-hydraulic servo control system[J]. 中国航空学报: 英文版, 2008, 21(4):378-384.

[7] 姚静, 孔祥东, 单东升, 等. 50MN自由锻造水压机电液伺服控制系统负载特性分析[J]. 机床与液压, 2006(8):101-103.

[8] Li F, Wang K, Ma C L, et al. Dynamic modeling and tracking control simulation for large electro-hydraulic servo system[J]. Applied Mechanics & Materials, 2013, 416/417:811-816.

[9] Zheng Q, Gaol L Q, Gao Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]// 46th IEEE Conf. on Decision and control. IEEE, 2007.

[10] Guo B Z, Zhao Z L. On the convergence of an extended state observer for nonlinear systems with uncertainty[J]. System & Control Letters, 2011, 60(6):420-430.

[11] Guo B Z, Zhao Z L. On convergence of nonlinear extended state observer for multi-input multi-output systems with uncertainty[J]. Control Theory & Applications Iet, 2012, 6(15):2375-2386.

[12] Chen Z Q, Sun M W, Yang R. On the stability of linear active disturbance rejection control[J]. Acta Automatica Sinica, 2013, 39(5):574-580.

[13] 陈星. 自抗扰控制器参数整定方法及其在热工过程中的应用[D]. 北京：清华大学，2008.

[14] Gao Z. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the American Control Conference. IEEE, 2003.