含转动副间隙的两转动并联机构动力学建模与动态特性分析

侯雨雷 井国宁 邓云蛟 杨彦东 曾达幸

燕山大学机械工程学院,秦皇岛,066004

0 引言

实际工况下，机构运动铰链的间隙是不可避免的，它的产生涉及到机械的加工制造、安装调试、材料形变、摩擦磨损等从设计到使用的各个方面[1-2]，而间隙的存在很大程度上会引起机构振动、噪声，致使精度下降、过度磨损、寿命缩短等。

近几十年来，众多学者对含间隙机构进行了大量研究。赵宽等[3]以含间隙的曲柄滑块机构为研究对象，研究了系统物理和几何参数的随机性对系统动力响应的影响。李仕华等[4]分别以销轴和两维指向机构为研究对象，结合“接触-分离”两状态模型，分析了不同重力环境下含间隙铰位置的运动轨迹及销轴与套筒碰撞力的变化规律。时兵等[5]针对大型重载机构虚拟样机中的间隙旋转铰，基于间隙矢量模型分析了铰链间隙对机构动力学特性的影响。ZHANG等[6]以平面3-RRR并联机构为研究对象，分析了多间隙下载荷、运动速度以及运动轨迹对机构性能的影响。FLORES等[7]对考虑润滑的含间隙机构的动力学进行了研究。VAREDI等[8]以接触力最小为优化目标，对含间隙曲柄滑块机构的质量进行优化，有效减小了冲击与振动。ZHANG等[9]以曲柄滑块机构为研究对象，分析了含转动副间隙的多体系统的性能优化。OLYAEI等[10]对含间隙的曲柄滑块机构进行控制，使机构由混沌运动转变为周期运动。RAHMANIAN等[11]研究了机构随间隙大小而变化的分岔图，分析了间隙对机构稳定性的影响。刘宏昭等[12]研究了构件柔性和铰链间隙对机构系统动力学特性的影响，并用Archard磨损模型对间隙运动副的磨损进行了预测。

接触碰撞[13]是含间隙机构的典型现象，而描述该现象所应用的接触力模型对求解结果有很大影响。BAI等[14]提出一种基于Lankarani-Nikravesh接触力模型与改进弹性模型的混合接触力模型。王庚祥等[15]将Flores接触模型中的常数刚度系数修正为非线性刚度系数而提出一种改进的接触力模型，并利用增广法对考虑球面副的4-SPS/CU并联机构进行动力学建模，分析了间隙对机构动态特性的影响。

并联机构以其比刚度大、结构紧凑、承载能力强、无累积误差等优点，广泛用于航空航天、医疗器械、人形机器人[16]等诸多领域。高精度、高可靠性装备对机构动力学特性提出更高要求，因此并联机构中间隙的存在对机构动力学的影响日益变得不容忽视。已有文献中含间隙机构的动力学建模主要集中在比较简单的平面机构，对含间隙的并联机构进行动力学分析还很少见。

本文在此背景下，提出一种修正的接触力模型，并验证其有效性；同时以含间隙RU-RPR(R为转动副，U为虎克铰，P为移动副)并联机构为研究对象，应用该修正的接触力模型对机构的动态特性予以分析。

1 含间隙RU-RPR的并联机构动力学方程的建立

如图1所示，RU-RPR两转动并联机构由固定平台、动平台以及连接两平台的两条支链组成，其中，分支2的移动副E的移动方向与该分支两转动副C、D轴线的公垂线平行，两分支中与固定平台相连的两转动副A、D的轴线相互平行且与虎克铰B的一条轴线平行，虎克铰的另一条轴线与转动副C的轴线重合[17]。固定坐标系o0x0y0z0与定平台相固连，o2x2y2z2为与动平台2相固连的局部坐标系，oixiyizi(i=1,3,4)为与构件i质心固连的局部坐标系，坐标原点oi为构件i的质心点，且各坐标系原点位于同一平面内。

图1 RU-RPR两转动并联机构示意图Fig.1 Schematic diagram of RU-RPR 2-DOFrotational parallel mechanism

RU-RPR并联机构含有4个活动构件，本文假设D处的转动副存在间隙，其他运动副处于理想状态。为便于描述该机构运动学状态，取机构的广义坐标为

(1)

式中，qj为构件j的质心坐标，j=1,2,3,4。

由于构件1、3、4均在xioiyi平面内运动，故构件1、3、4在定坐标系中可写成矩阵形式：

qi=[xiyiθi]T

(2)

式中，(xi，yi)为构件i的质心在定坐标系下的坐标；θi为局部坐标系在定坐标系下相对于z0的转角。

机构动平台具有2个转动自由度，可以先绕z2轴转动，再绕y2轴转动。若以z-y-x型欧拉角表示动平台上局部坐标系相对于定坐标系的转动，则可以写成矩阵形式 [θ2β20]T，因此动平台在定坐标系中可表示为

q2=[x2y2θ2β2]T

(3)

RU-RPR并联机构中关节点A、B、C处的约束方程可写为

ΦP=rl+AlrPl-rh-AhrPh=02×1

(4)

式中，rl、rh为铰链连接的两个构件l和h质心点的位置坐标，rl=[xlyl]T，rh=[xhyh]T；rPl、rPh为关节点A、B、C分别在局部坐标系ol和oh下的位置；Al、Ah为旋转矩阵。

构件2与3始终垂直，因此有

Φ23=θ2-θ3-π/2=0

(5)

由机构结构组成可知，E处移动副导路方向和C处转动副轴线垂直，则连线o2C与连线o3o4垂直。令d、s分别为o2C与o3o4的方向向量，且构件3、构件4转动角度相同，即可得到E处移动副的2个约束关系ΦE1、ΦE2：

ΦE1=s·d=0

(6)

ΦE2=θ4-θ3=0

(7)

此外，还有2个驱动约束方程：

(8)

(9)

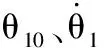
D处转动副含有间隙，由接触力进行约束；式(4)～式(9)组成含间隙RU-RPR并联机构的整体约束方程(包含理想运动副约束与驱动约束)：

(10)

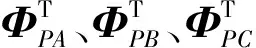
式(10)关于时间的一阶导数即为该并联机构的速度约束方程：

(11)

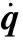
式(10)关于时间的二阶导数即为该并联机构的加速度约束方程：

(12)

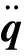
利用牛顿-欧拉法建立系统带拉格朗日乘子的动力学方程：

(13)

式中，M为系统的质量矩阵；λ为拉格朗日乘子矢量，与和运动副相连的构件之间的内力、内力矩相关；g为广义力矢量，包含外力、外力矩。

式(12)、式(13)可以组成一个微分代数方程：

(14)

(15)

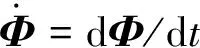
式中，α、ξ为大于0的修正参数。

从而达到衰减系统违约量的目的。

2 转动副间隙建模

转动副间隙模型如图2所示，其中，Ou、Ow分别表示构件u上轴承和构件w上轴的中心位置，rOu、rOw分别是轴承和轴的中心在固定坐标系下的位置矢量，则轴承和轴的间隙矢量为

e=rOk-rOu

(16)

其单位矢量为

n=e/e

(17)

式中，e为间隙矢量的幅值。

Qu、Qw分别表示轴承和轴碰撞时的碰撞点，rQu、rQw分别为轴承和轴碰撞时相应的碰撞点在固定坐标系下的位置矢量，即

rQk=rOw+Rkn

(18)

k=u,w

式中，Ru、Rw分别为轴承与轴的半径。

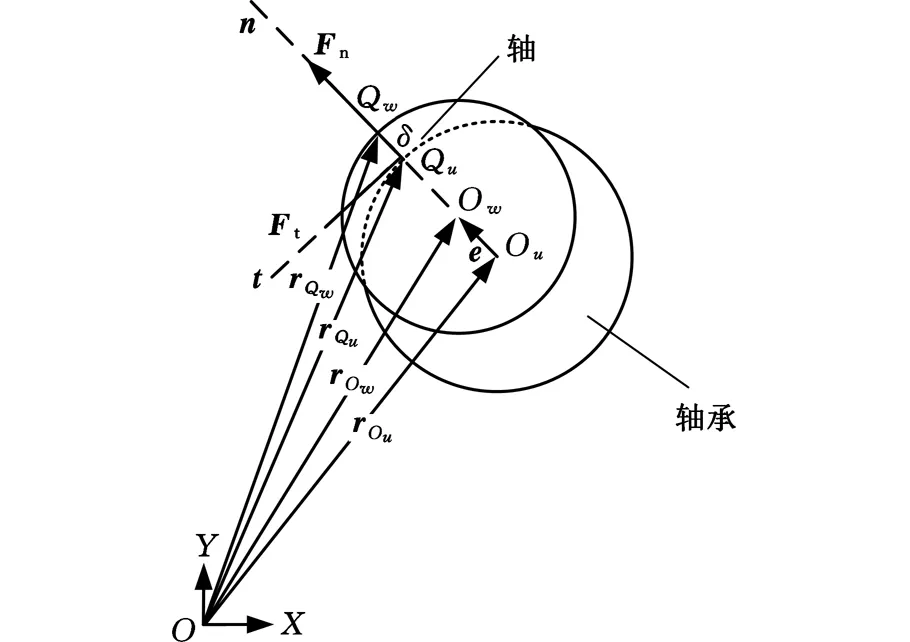
图2 转动副间隙模型Fig.2 Gap model of the rotation pair

式(18)两边对时间求导，可得碰撞点速度：

(19)

将碰撞点的相对速度投影到碰撞平面的切向和法向平面，可得相对的法向速度vn和切向速度vt：

(20)

其中，切向矢量t可以通过将n逆时针旋转90°获得。

轴承和轴的穿透深度为

δ=e-r

(21)

式中，r为半径间隙，r=Ru-Rw。

δ≥0时，轴承与轴接触，反之，轴承与轴没有接触。

分析每次碰撞的初始碰撞速度及碰撞面的方向时，精确检测出碰撞点非常重要。轴承与轴发生碰撞的条件是

δ(tn)δ(tn+1)≤0

(22)

式中，δ(tn)、δ(tn+1)分别为碰撞前后的穿透深度。

碰撞过程中必然产生碰撞力，此处应用修正的接触力模型来计算法向接触力(后文将详细介绍)并用AMBRSIO[19]提出的修正Coulomb摩擦力法则来计算切向接触力，轴对轴承的切向接触力的表达式为

Ft=-cfcdFnvt/|vt|

(23)

(24)

式中，cf为摩擦因数；cd为动态修正系数；v0、v1为给定的速度界限。

3 接触力模型的修正与校验

3.1 接触力模型的修正

Lankarani-Nikravesh接触力模型既涉及碰撞过程中的能量损失，又考虑碰撞体的材料属性、局部弹性变形以及碰撞速度等信息[2]，广泛用于含间隙机构的分析中，其表达式为

(25)

刚度系数表达式为

(26)

式中，νk、Ek、Rk分别为泊松比、弹性模量和半径；下标u、w分别表示构件u上的轴承和构件w上的轴。

阻尼系数可表示为

(27)

Lankarani-Nikravesh接触力模型还存在一些不足：一方面，其刚度系数忽略了碰撞体间嵌入深度与接触刚度的耦合关系，仅适用于大间隙、小载荷的接触问题；另一方面，其阻尼系数使用范围受恢复系数的限制，仅适用于恢复系数较大(碰撞体的材料为硬材料)的情况，不适用于恢复系数较小(碰撞体的材料为软材料)的碰撞问题。

式(26)所示的Hertz刚度系数K为一定值，仅与碰撞体的材料属性、曲率半径相关，而未考虑与碰撞体之间嵌入深度的关系。另外，Hertz接触公式仅适用于大间隙、小载荷的接触问题[2]。

文献[20]基于改进的弹性基础模型得到了载荷P与变形量(穿透深度)δ间的关系为

(28)

式中，ΔR为轴承与轴之间的半径差。

文献[2]根据式(28)，提出了非线性刚度系数，扩展了刚度系数适用间隙尺寸的范围，可以应用于各种尺寸大小的转动副间隙，其刚度系数的表达式为

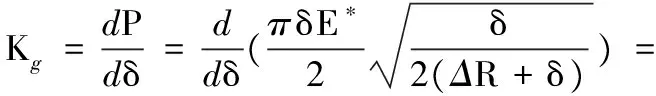
(29)

文献[21]对绝大多数含有阻尼项的接触力模型进行了对比研究，结果表明Lankarani-Nikravesh接触力模型仅适用于恢复系数较大的情况，并且建议恢复系数大于0.7。此外，通过该文得到的不同接触力模型下的力与压痕关系可以推得，Lankarani-Nikravesh接触力模型耗散较少能量，文献[22]也表达了相同的观点。

相比Lankarani-Nikravesh接触力模型，Flores接触力模型的结构形式相对简单，便于数值计算，而且使用范围不受恢复系数的限制，并适用于软材料、硬材料的接触碰撞情形。Flores的接触力表达式中的阻尼项为

(30)

针对Lankarani-Nikravesh接触力模型的不足，本文结合式(29)、式(30)提出修正的接触力模型的表达式为

(31)

3.2 修正接触力模型的校验

文献[23]以曲柄滑块机构为研究对象，考虑转动副间隙，基于Lankarani-Nikravesh接触力模型，针对不同的间隙大小与驱动速度进行动力学仿真计算，对比数值仿真与实验分析得到的滑块加速度，从而验证含间隙转动副模型的有效性。本文基于修正的接触力模型(式(31))，将仿真分析结果与文献[23]的实验数据进行对比，以验证修正模型的有效性。

含间隙曲柄滑块机构如图3所示，曲柄滑块机构的基本参数、动力学仿真参数分别如表1、表2所示，与文献[23]一致。

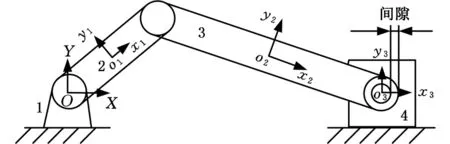
图3 含间隙曲柄滑块机构示意图Fig.3 Schematic diagram of slider crank mechanism with clearance

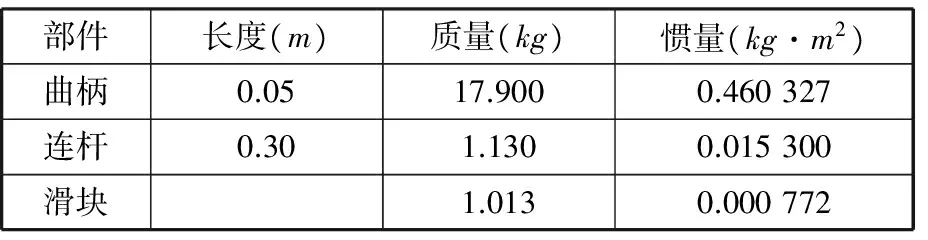
部件长度(m)质量(kg)惯量(kg·m2)曲柄0．0517．9000．460327连杆0．301．1300．015300滑块1．0130．000772

图4、图5所示分别为驱动速度200 r/min时不同的间隙尺寸下的实验分析结果[23]与修正模型的仿真分析结果。仿真结果表明，含间隙曲柄滑块机构的滑块加速度相对于无间隙的滑块加速度有所波动，且随着间隙的增大，滑块的加速度波动更加剧烈，波动频率则下降；同时，波动的幅值与实验数据相一致，而数据上的偏差则是由模型中杆件、关节的柔性及测量因素等导致的。对比结果表明，修正的接触力模型可以有效分析含间隙机构动力学响应。

表2 含间隙曲柄滑块机构动力学参数

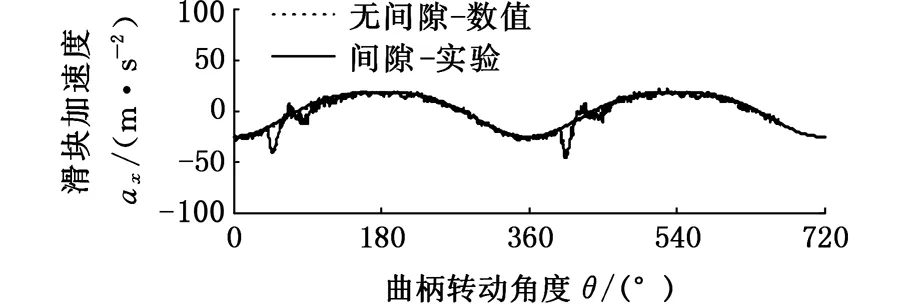
(a)间隙为0.1 mm

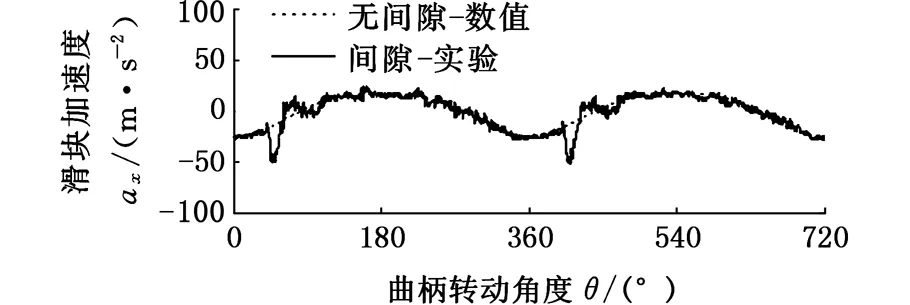
(b)间隙为0.25 mm

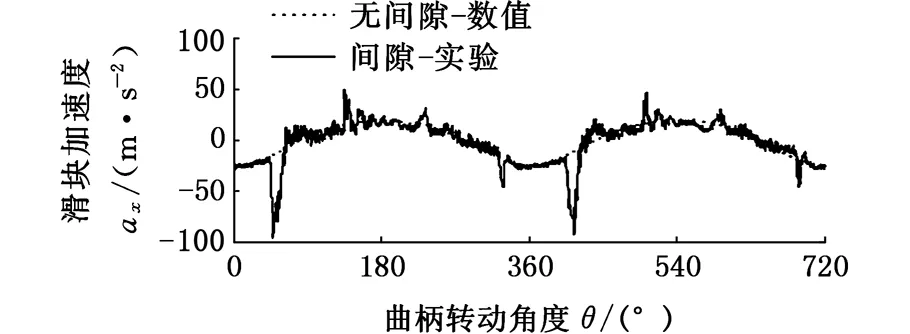
(c)间隙为0.5 mm

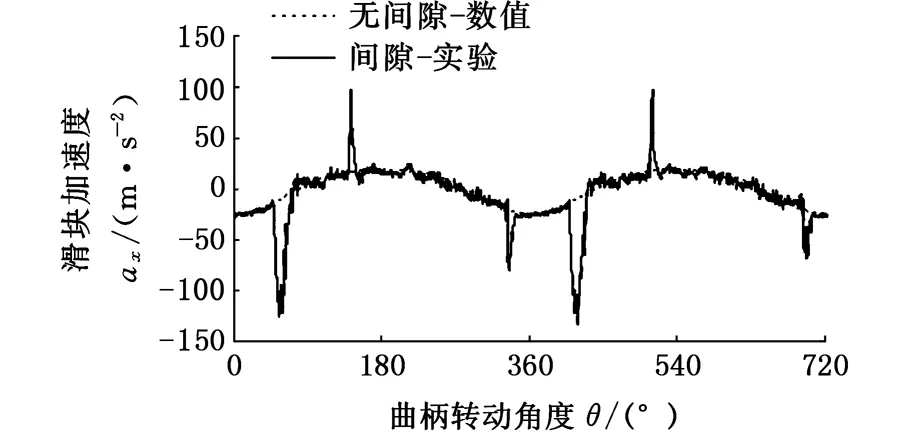
(d)间隙为1 mm图4 不同间隙尺寸下的实验分析结果[23]Fig.4 Experimental data with different clearances[23]

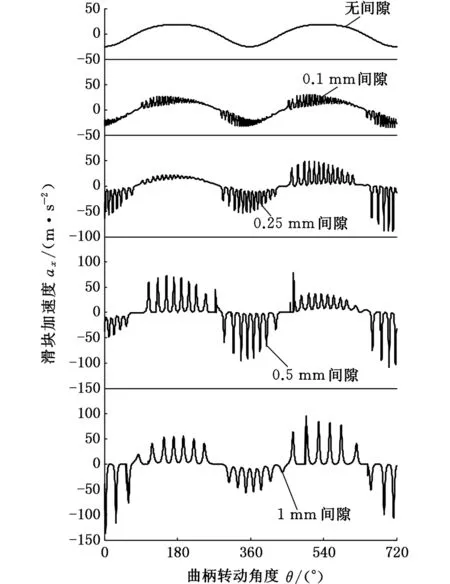
图5 不同间隙尺寸下的修正接触力模型仿真分析结果Fig.5 Simulation results of modified contact force models with different clearances

4 含间隙RU-RPR并联机构的动力学仿真

考虑避开机构奇异位形[24]，不妨设定RU-RPR并联机构的运动规律为

(32)

RU-RPR机构杆件形状见图1，多选用长方形和圆柱形，其材料为45钢，则可得到RU-RPR机构基本参数，如表3所示，机构动力学数值求解流程如图6所示，机构动力学仿真参数如表4所示。

根据流程图应用四阶Runge-Kutta法予以求解，借助MATLAB软件编制程序并进行计算，求得两种不同摩擦因数下(cf=0.01，0.05)间隙并联机构的动态特性；同时，在ADAMS动力学仿真软件中建立RU-RPR机构理想运动副的动力学模型，求得理想运动副条件下机构的动力学响应并将数据导入MATLAB软件中，与间隙运动副条件下的响应曲线进行对比，结果分别如图7、图8所示。

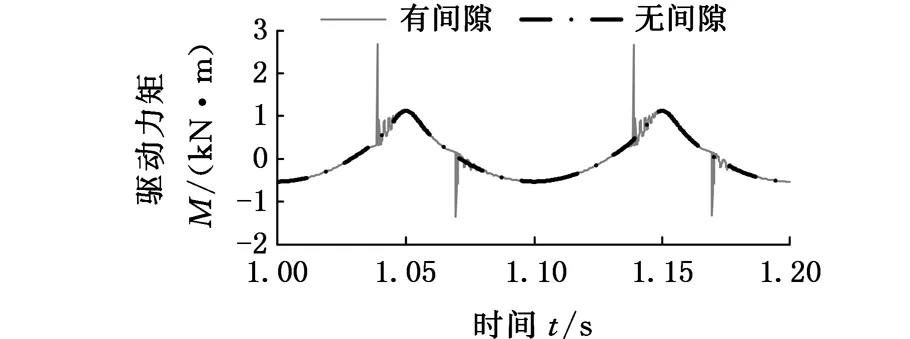
图7表示摩擦因数cf=0.01时D处转动副间隙对该并联机构动态特性的影响。由图7a～图7c可以看出，含间隙条件下并联机构的角加速度、加速度和驱动力矩的变化曲线与理想条件下的整体运动趋势一致，在一定程度上说明了所建立的机构动力学方程及其求解的正确性。图7a显示，间隙的存在会使动平台绕z0轴转动的角加速度相对于无间隙时的角加速度发生剧烈的波动，此时角加速度的峰值达到5973 rad/s2；角加速度剧烈波动的时间点与图7d中嵌入深度变化较快的时间点是吻合的，如在t=1.07 s附近，嵌入深度发生突变，轴与轴承之间分离之后剧烈碰撞，此时角加速度曲线也发生突变，说明碰撞是导致速度波动的原因；图7b中动平台沿x方向的加速度曲线、图7c中A处驱动力矩曲线变化趋势与图7a中的一致，机构呈现出非线性。

表3 RU-RPR并联机构基本参数

图6 含间隙RU-RPR并联机构动力学数值求解流程图Fig.6 Flow diagram of numerical solution of RU-RPR parallel mechanism with clearance

参数数值轴承半径Ru(mm)15恢复系数ce0．6间隙大小r(mm)0．3驱动频率ω(rad/s)20πBaumgarte修正系数α30Baumgarte修正系数β30弹性模量Eu、Ew(GPa)200泊松比νu、νw0．3积分步长dt(ms)0．01

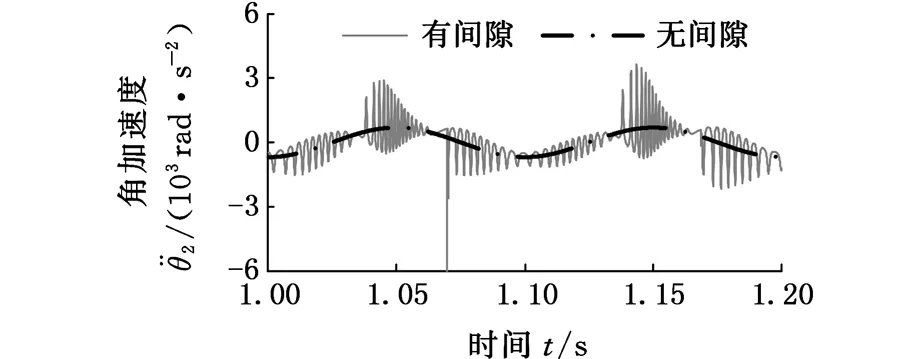
(a)动平台绕z0轴转动的角加速度曲线

(b)动平台沿x方向的加速度曲线

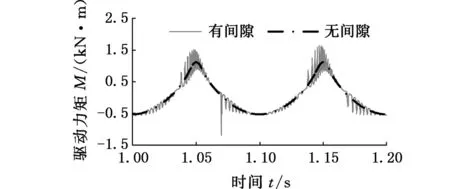
(c)A处驱动力矩曲线

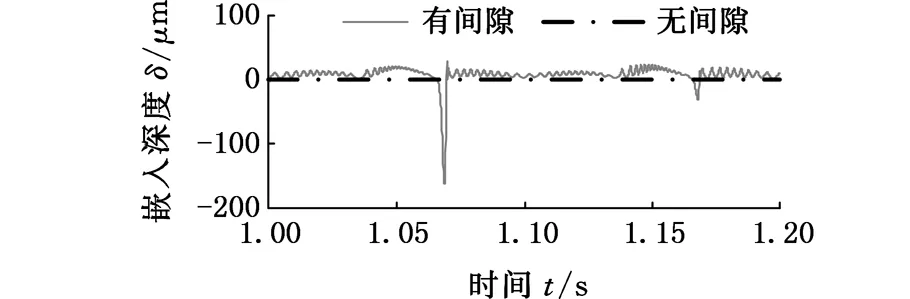
(d)嵌入深度曲线图7 cf =0.01时RU-RPR并联机构动态特性Fig.7 Dynamic characteristics of the RU-RPR parallel mechanism with cf=0.01

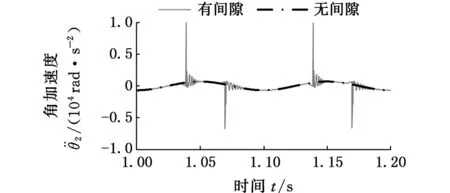
(a)动平台绕z0轴转动的角加速度曲线

(b)动平台沿x方向的加速度曲线

(c)A处驱动力矩曲线

相比于图7，图8a中角加速度曲线非线性特性减弱，呈现出明显的周期性，而其峰值为9948 rad/s2，增大了66.5%，图8b～图8d亦表现出相似特性。

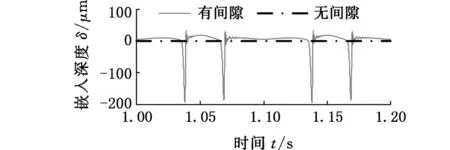
(d)嵌入深度曲线图8 cf =0.05时RU-RPR并联机构动态特性Fig.8 Dynamic characteristics of the RU-RPR parallel mechanism with cf=0.05

对比不同摩擦因数下机构的动态特性可以得出：随着摩擦因数的增大，机构非线性特性减弱，但冲击程度变得更为严重，其原因是摩擦因数的增大导致系统耗散更多的能量，从而变得稳定；摩擦因数的增大导致切向接触力增大，进而加重了接触碰撞的程度。

5 结论

(1)采用微分代数形式的方程建立了含间隙RU-RPR并联机构动力学模型，并针对Lankarani-Nikravesh接触力模型的不足，提出一种修正的接触力模型，并校验其有效性，扩展了应用间隙的适用范围。

(2)应用修正的接触力模型并借助四阶Runge-Kutta法对不同摩擦因数下含间隙RU-RPR的并联机构进行动态特性仿真分析，结果表明摩擦因数的增大使系统耗散更多的能量且切向接触力增大，机构表现出非线性特性减弱，而冲击程度增大的现象。

[1] FLORES P. Dynamic Analysis of Mechanical Systems with Imperfect Kinematic Joints[D]. Braga, Portugal：Universidade Do Minho, 2004.

[2] 白争锋. 考虑铰间间隙的机构动力学特性研究[D]. 哈尔滨：哈尔滨工业大学, 2011.

BAI Zhengfeng. Research on Dynamic Characteristics of Mechanism with Joint Elearance[D]. Harbin：Harbin Institute of Technology, 2011.

[3] 赵宽, 陈建军, 曹鸿钧, 等. 含间隙曲柄滑块系统动力响应的随机性分析[J]. 振动与冲击, 2014, 33(11): 130-135.

ZHAO Kuan, CHEN Jianjun, CAO Hongjun, et al. Randomness Analysis of Dynamic Responses of a Slider-crank System with Clearances[J]. Journal of Vibration and Shock, 2014, 33(11): 130-135.

[4] 李仕华, 冯伟波, 秦利,等. 不同重力环境下含间隙铰位置和碰撞力[J]. 机械工程学报, 2015, 51(17): 52-58.

LI Shihua, FENG Weibo, QIN Li, et al. Effect of Different Gravity Environment on the Position and Collision Force of Joint with Clearance[J]. Journal of Mechanical Engineering, 2015, 51(17): 52-58.

[5] 时兵, 金烨. 面向虚拟样机的机构间隙旋转铰建模与动力学仿真[J]. 机械工程学报, 2009, 45(4): 299-303.

SHI Bing, JIN Ye. Dynamic Simulation and Modeling of Revolute Clearance Joint for Virtual Prototyping[J]. Journal of Mechanical Engineering, 2009, 45(4): 299-303.

[6] ZHANG X C, ZHANG X M, CHEN Z. Dynamic Analysis of a 3-RRR Parallel Mechanism with Multiple Clearance Joints[J]. Mechanism and Machine Theory, 2014, 78(8): 105-115.

[7] FLORES P, AMBROSIO J, CLARO J C P, et al. A Study on Dynamics of Mechanical Systems Including Joints with Clearance and Lubrication[J]. Mechanism and Machine Theory, 2006, 41(3): 247-261.

[8] VAREDI S M, DANIALI H M, DARDEL M, et al. Optimal Dynamic Design of a Planar Slider-crank Mechanism with a Joint Clearance[J]. Mechanism and Machine Theory, 2015, 86(1): 191-200.

[9] ZHANG Zhenhua, XU Liang, FLORES P, et al. A Kriging Model for Dynamics of Mechanical Systems with Revolute Joint Clearances[J]. Journal of Computational & Nonlinear Dynamics, 2014, 9(3): 310-319.

[10] OLYAEI A A, GHAZAVI M R. Stabilizing Slider-crank Mechanism with Clearance Joints[J]. Mechanism and Machine Theory, 2012, 53(3): 17-29.

[11] RAHMANIAN S, GHAZAVI M R. Bifurcation in Planar Slider-crank Mechanism with Revolute Clearance Joint[J]. Mechanism and Machine Theory, 2015, 91(4): 86-101.

[12] 邓培生, 原大宁, 刘宏昭, 等. 考虑杆件柔性的间隙机构系统磨损分析[J]. 中国机械工程, 2016, 27(2): 143-149.

DENG Peisheng, YUAN Daning, LIU Hongzhao, et al. Wear Analysis on Intermittent Mechanism Systems Inclulding Flexible Bar[J]. China Mechanical Engineering, 2016, 27(2): 143-149.

[13] 董富祥, 洪嘉振. 多体系统动力学碰撞问题研究综述[J]. 力学进展, 2009, 39(3): 352-359.

DONG Fuxiang, HONG Jiazhen. Review of Impact Problem for Dynamics of Multibody System[J]. Advances in Mechanics, 2009, 39(3): 352-359.

[14] BAI Zhengfeng, ZHAO Yang. A Hybrid Contact Force Model of Revolute Joint with Clearance for Planar Mechanical Systems[J]. International Journal of Non-linear Mechanics, 2013, 48(1): 15-36.

[15] 王庚祥, 刘宏昭. 考虑球面副间隙的4-SPS/CU并联机构动力学分析[J]. 机械工程学报, 2014, 51(1): 43-51.

WANG Gengxiang, LIU Hongzhao. Dynamics Analysis of 4-SPS/CU Parallel Mechanism with Spherical Joint Clearance[J]. Journal of Mechanical Engineering, 2014, 51(1): 43-51.

[16] 侯雨雷, 汪毅, 范建凯, 等. 3-PCSS/S球面并联肩关节机构优化与仿生设计[J]. 机械工程学报, 2015, 51(11): 16-23.

HOU Yulei, WANG Yi, FAN Jiankai, et al. Optimization and Bionic Design of 3-PCSS/S Spherical Parallel Mechanism for the Shoulder Joint[J]. Journal of Mechanical Engineering, 2015, 51(11): 16-23.

[17] HOU Y L, ZENG D X, ZHANG Z Y, et al. A Novel Two Degrees of Freedom Rotational Decoupled Parallel Mechanism[J]. Applied Mechanics & Materials, 2012, 215-216: 293-296.

[18] FLORES P, MACHADO M, SEABRA E, et al. A Parametric Study on the Baumgarte Stabilization Method for Forward Dynamics of Constrained Multibody Systems[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(1): 73-82.

[20] LIU C S, ZHANG K, YANG R. The Fem Analysis and Approximate Model for Cylindrical Joints with Clearances[J]. Mechanism and Machine Theory, 2007, 42(2): 183-197.

[21] ALVES J, PEIXINHO N, SILVA M T D, et al. A Comparative Study of the Viscoelastic Constitutive Models for Frictionless Contact Interfaces in Solids[J]. Mechanism and Machine Theory, 2015, 85(3): 172-188.

[22] MACHADO M, MOREIRA P, FLORES P, et al. Compliant Contact Force Models in Multibody Dynamics: Evolution of the Hertz Contact Theory[J]. Mechanism and Machine Theory, 2012, 53(3): 99-121.

[23] FLORES P, KOSHY C S, LANKARANI H M, et al. Numerical and Experimental Investigation on Multibody Systems with Revolute Clearance Joints[J]. Nonlinear Dynamics, 2011, 65(4): 383-398.

[24] 侯雨雷, 张占叶, 胡鑫喆, 等. 新型两转动自由度完全解耦并联机构及其特性[J]. 哈尔滨工业大学学报, 2014, 46(9): 80-85.

HOU Yulei, ZHANG Zhanye, HU Xinzhe, et al. A Novel 2-DOF Fully Decoupled Rotational Parallel Mechanism and Its Characteristics[J]. Journal of Harbin Institute of Technology, 2014, 46(9): 80-85.