考虑夹具的车门刚度特性分析及误差研究

宋 凯 胡金花 高 晖 石少亮

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南湖大艾盛汽车技术开发有限公司，长沙，410082

0 引言

实际工程项目中，由试验误差和有限元分析误差导致的试验数据与仿真结果不一致是一个亟待解决的难题。为了提高试验和仿真的分析精度，国内外学者对此都进行了大量研究。GOPALAKRISHNAN等[1]利用边值的伴随场理论来控制小特征消除对工程分析误差的影响；LI等[2]基于最小二乘法和函数库补偿法，研究了倾斜误差的补偿方法；唐建国等[3]提出了一种面向CAE的简化模型误差评估、边界补偿和信息重用方法。以上方法主要研究的是有限元建模过程中小特征消除误差评估与补偿方法，忽略了试验过程可能出现的误差。

虽然许多学者在有限元分析时引入了一定的建模误差，比较了简化建模与详细建模的相对误差，但综合考虑各种因素，对汽车覆盖件的刚度误差研究还不完善[4-6]。文献[7-8]重点研究了车身覆盖件的刚度仿真分析与试验，讨论了影响刚度试验结果的因素，证明了模拟的实际工况与实际工况本身有偏差。然而，针对汽车车门仿真分析与试验数据的误差研究相对较少。

本文从工程实际角度出发，从试验和仿真两方面同时寻找误差来源并建立了试验数据采集误差模型、试验柔性变形误差模型、仿真夹具误差模型和仿真测点误差模型；通过误差极限合成理论建立了试验误差模型，利用灵敏度分析方法和等距面误差法推导了仿真误差模型；用代数和法修正误差，缩小了试验和仿真与真实车门刚度特性之间的相对误差，验证了车门刚度分析对工程约束条件具有很高的敏感度，揭示了误差在刚度分析中的传递规律和累积效应。以某车门为例，验证了误差模型的准确性。

1 车门-夹具系统刚度特性分析

车门刚度性能研究方法主要有解析法、试验法和仿真法。解析法侧重于理论分析，其基本原理是将车门结构简化成质量点、阻尼和弹簧，通过质量点间的关联求取质量-弹簧数学模型，但由于结构比较复杂，该方法往往精度较低，一般用于定性分析。试验法是精度最高、应用最广泛的方法，包括车门刚强度试验、模态试验及疲劳耐久性试验，但试验成本高、周期长，一般用于对标车试验和摸底试验。仿真法依靠CAE软件，直接获得车门各个部件的变形、应力等相关参数，便于进行结构设计、优化及轻量化，但有限元分析导致的离散化和难以真实模拟实际的受力过程，使结果产生一定误差。

以上三种方法在分析车门刚度时，不考虑原始测点带有工程约束的问题，获得的位移参数不能满足工程实际的需要，导致数值仿真结果与试验数据偏差较大。因此本文介绍了一种带工程约束的车门-夹具系统刚度特性分析算法，考虑试验过程中接触力、夹紧力及重力的影响，根据做功相等原理，建立车门-夹具系统的刚度力学模型：

E=U+W

(1)

式中，E为外力做功；U为工件加载点变形能；W为接触势能。

式(1)展开式为

(2)

式中，FW为外载荷；X1为加载点实际测试位移；KW为工件刚度矩阵；FP为试验过程中相应的接触力；Δp为装夹元件处的接触变形。

根据工件静力平衡约束可得

GPFP=-GaFa-Wg

(3)

GP=[G1G2…Gk]

(4)

j=1,2,…，k

Ga=

(5)

(6)

式中，Ga为夹紧力；Wg为重力矩；ni为工件在第i个装夹元件接触位置rci处的单位内法向量，i=1，2，…，k+n；ti、bi分别为工件在第i个接触点处的两个正交的单位切向量。

显然，根据式(3)求得相应的接触力FP后，根据Hooke定理可知工件加载点的真实变形为

(7)

2 误差模型建立

传统的误差分析方法主要有基于仿真误差的补偿方法[3-6]和基于试验误差的修正方法[2,8]。针对试验法和仿真法所得结果偏差较大的问题，本文提出了综合考虑试验误差和仿真误差的方法，分析流程见图1。

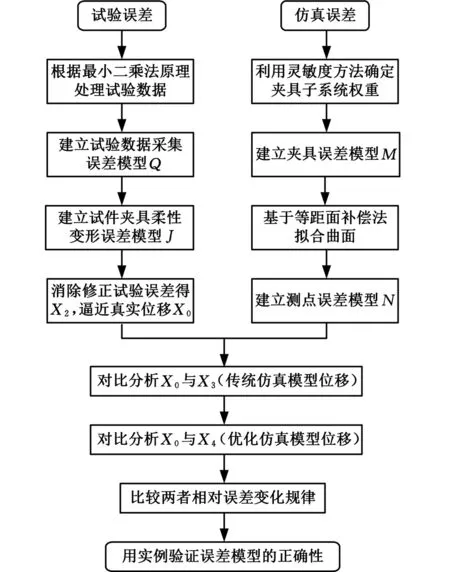
图1 考虑夹具的车门刚度特性误差分析Fig.1 Error analysis of door stiffness characteristic considering fixture

由于真值X0无法求得，只有理论意义，故在本文中，认为真值X0近似等于试验修正值，即

X0≈X2=X1+ε1

(8)

(9)

(10)

式中，ε1为试验偏差值；ε2为仿真偏差值；δ1为仿真相对误差；δ2为仿真优化后相对误差；X0为真实值；X2试验修正值；X3为仿真初始值；X4为仿真优化值。

2.1 试验误差分析

2.1.1数据采集误差的影响

数据采集误差包括试验台架间隙误差、环境误差、数据后处理误差等，这些数据的不确定性必然会影响最终试验数据的准确度。因此为保证试验过程中数据的准确性，在刚度试验开始前，确保试件及试验装置各部分接触良好，消除试验台架系统的间隙误差εx；利用线性插值法对试验过程取点进行插值，构建合理模型，如试验过程中可采取重复m次试验和分n步加载的方法。对试验数据位移X1_i和载荷F采用拟合直线来模拟，设直线方程为

X=AF+B

(11)

测试中所有测点数据与经处理后的拟合直线所求回归值的偏差平方和φ最小，即求取实测值X1_i与估计计算值X1_ j的离差最小：

(12)

求出未知参数A和B，得到试验拟合直线相关度

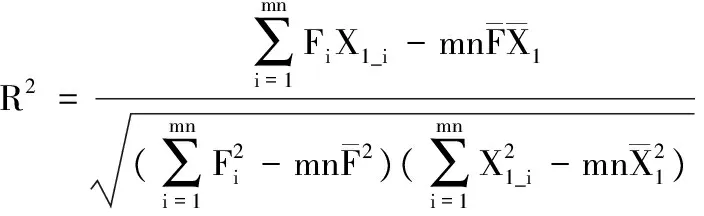
(13)

相关度越接近1，越说明试验数据紧密分布于拟合直线附近。

试验过程中产生的试验台架系统对刚度测点产生的误差模型可以表示为

(14)

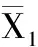
2.1.2柔性变形误差的影响

对车门进行刚度试验时，由于车门自然下垂，因此需要对锁芯施加载荷，在车门锁处安装刚性替代件，延伸出加载臂；需要约束锁芯时，在门锁处安装刚性替代件与连接杆。装夹装置在实际试验中有一定的局部轻微变形，监测球铰处柔性变形为Δl，试验误差修正系统见图2。

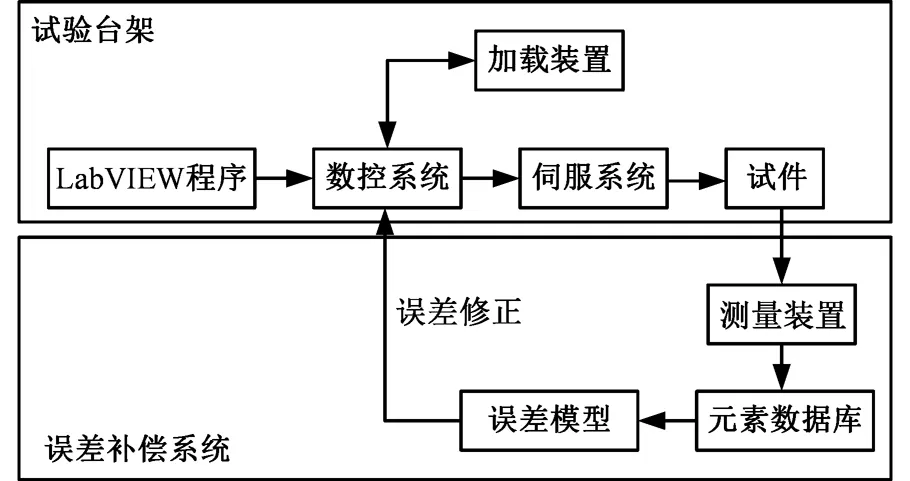
图2 试验误差修正系统示意图Fig.2 Test error correction system diagram

试验过程中产生的柔性变形对刚度测点产生的误差模型为

εJ=(D-d)Δl/D

(15)

式中，εJ为柔性变形对测点变形的影响位移；D为车门铰链侧与锁侧夹具之间的距离；d为测点位置与锁侧夹具之间的距离。

2.1.3试验误差合成

假设测量过程中有t个单项已定系统误差Δ1、Δ2、…、Δt，s个单项未定系统误差γ1、γ2、…、γs，q个单项随机误差σ1、σ2、…、σq。各误差间互不相关时，各测量结果总的极限误差为

(16)

试验数据采集误差具有未定性，并服从一定的概率分布；柔性变形误差具有已定性，大小和方向均已掌握。利用上述极限误差合成理论，对试验数据采集误差、柔性变形误差进行合成，得到了试验误差模型：

(17)

2.2 仿真误差分析

2.2.1夹具模型误差的影响

车门刚度有限元分析不能忽略一些试验夹具的影响，因此采用灵敏度分析方法估计夹具带来误差的影响，再在保证满足分析精度的前提下，重点研究夹具模型误差的影响。

文献[9]研究表明，对含n个夹具子系统的模型，其夹具模型误差可表示为夹具模型误差的函数，展开为各夹具子系统(p1，p2，…，pn)误差的函数：

εM=f0(e1，e2，…，en)

(18)

式中，ei为夹具子系统i的相对误差，i=1，2，…，n。

在e1=e2=…=en= 0处利用Taylor级数展开方法对误差函数进行推导，得到夹具模型误差[9]：

(19)

利用灵敏度分析方法求取夹具子系统的影响权重wi，具体方法如下：

(1)计算模型总体误差E0，再取子模型i相对误差ei为灵敏度分析初始值；

(2)令子模型的相对误差ei=0，通过神经网络计算此时的总体误差值Ei；

(3)计算整体模型对各子模型的灵敏度si=|Ei-E0|；

2.2.2测点误差的影响

试验测头通常是球体，而数值仿真中目标点直接取相应区域节点位移，因此利用等距面法[10]对节点位移进行处理，求出节点位置补偿矢量，得到试验测点坐标。

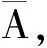
(20)

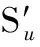
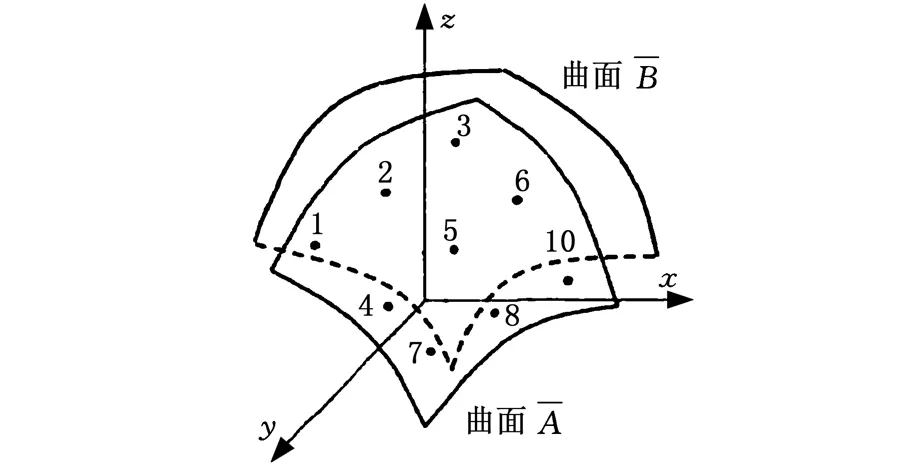
图3 等距面误差补偿Fig.3 Isometric surface error compensation

εN=P(u,v)±S(u,v)=rn(u,v)

(21)

夹具模型误差和测点误差相互独立、互不影响，总的仿真误差模型为

(22)

3 实例分析验证

以某轿车前门为研究对象，采纳林怡青等[11]的试验误差控制三原则，建立相应的误差模型。试验和仿真采用的是位移法，为了客观比较误差，实例中采取比较误差修正前后加载点的位移。

3.1 某车前门刚度试验修正

如图4所示，对某车门进行扭转刚度试验，前侧门经过3次重复试验，车门上扭测点位移为4.437 mm，下扭测点位移为2.577 mm。

图4 车门扭转刚度示意图Fig.5 Torsion stiffness of door

按照前文所述，考虑试验误差的影响，将试验及试验数据进行修正处理，具体实施如下：①首预加载荷450 N，消除试验台架及车门之间的系统间隙εx=0.186 mm；②在试验测试位置和车门锁芯位置设置位移传感器，得到其载荷F与位移X1的相关数据；③重复3次车门刚度试验，每次试验分10步加载，得到载荷Fi与位移X1_i，利用最小二乘法原理进行线性拟合。由图5可以看出，试验数据都密集分布于拟合直线附近，证明拟合直线在车门完好、无塑性变形的情况下能够有效预测其位移变化，在一定程度上减小了数据采集误差。

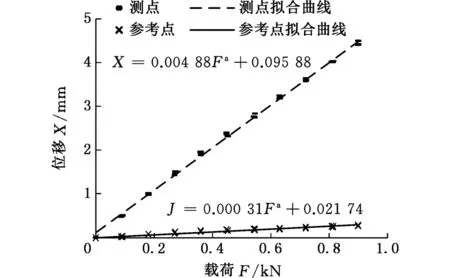
(a)前侧门上扭刚度试验结果

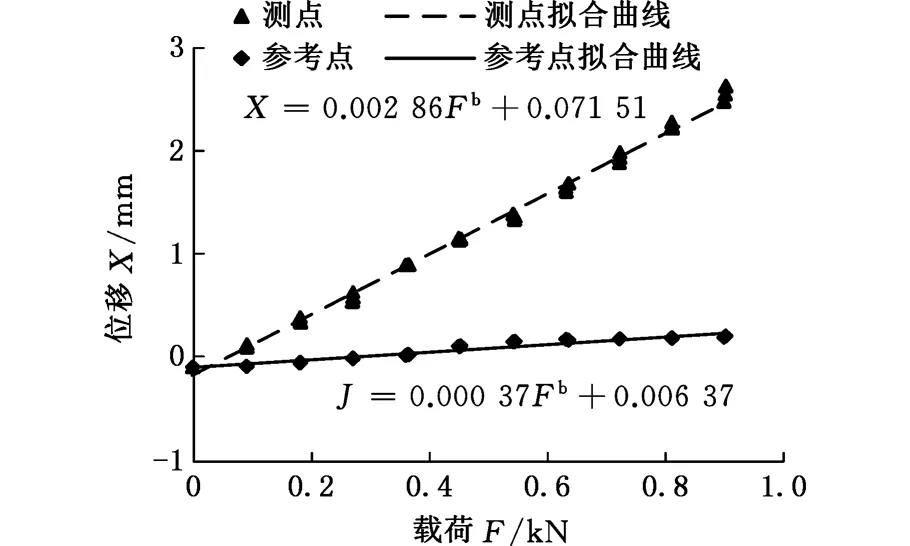
(b)前侧门下扭刚度试验结果图5 前侧门扭转刚度试验结果Fig.5 Test results of torsion stiffness on front door

考虑鱼眼轴承柔性变形对测点刚度的影响，将式(15)代入下式：

X2=X-εJ=X-(D-d)Δl/D

(23)

式中，X为消除试验数据采集误差后的测点位移；εJ为测点在鱼眼轴承微变形影响下的实际柔性变形；Δl为鱼眼轴承参考点的位移。

求出对测点进行柔性变形误差补偿后的修正试验结果。把数据代入式(23)得出上扭、下扭的表达式：

(24)

(25)

式中，上标a、b分别表示上扭和下扭；F为加载载荷。

从而求出试验修正位移X2，逼近真实值X0。表1所示为试验误差修正前后的刚度，对比发现，在对试验进行误差修正后，上扭刚度误差减小了5.5%，下扭刚度误差减小了14.7%。

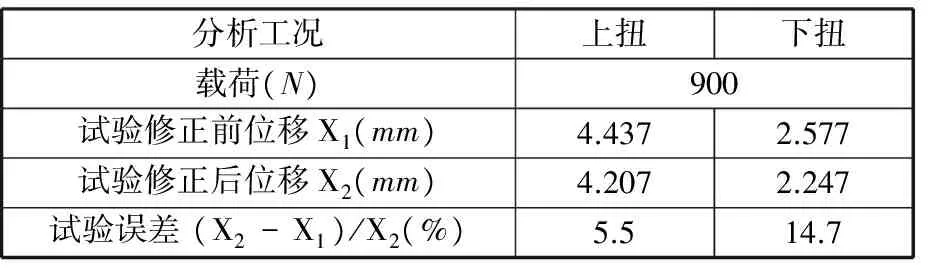
表1 试验修正前后的刚度

3.2 传统模型建立及结果

建立前侧门的传统有限元模型，车门处于关闭状态时，约束车门铰链与车身安装点处6个方向的自由度，并放开主副铰链轴线自由度，约束锁体鱼嘴中心处的3个平动自由度，具体加载方式如下，上扭加载点：I平面上，C线以下25 mm位置；下扭加载点：I平面上与T线成45°位置，车身坐标系下Y向由内板侧向外板侧分别施加900 N的均布力；I平面、C线和T线的定义如图6所示。

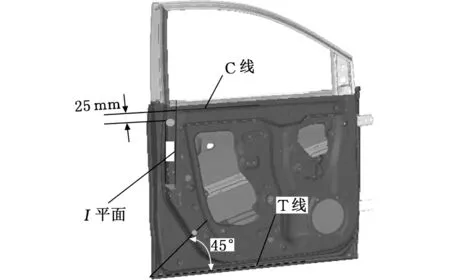
图6 I平面、C线和T线定义图Fig.6 Definitions of I-Plane, C-Line and T-Line

通过软件计算可知，前侧门加载900 N时，上扭刚度对应位移为1.532 mm，下扭刚度对应位移为0.794 mm。由图7可知，两条直线的斜率即为扭转刚度值，上扭刚度为587.4 N/mm，下扭刚度为1 133.8 N/mm。

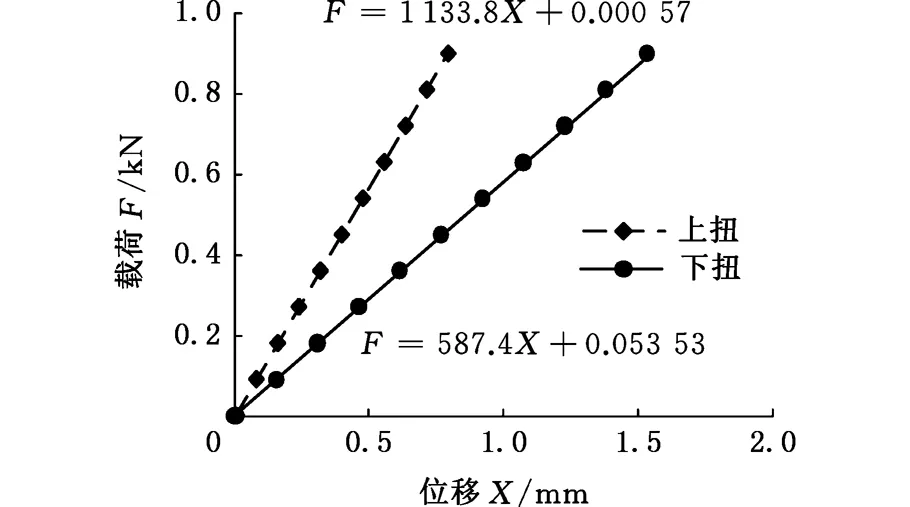
图7 前侧门扭转刚度分析结果图Fig.7 Analysis results of torsion stiffness on front door

3.3 优化模型建立及结果

考虑仿真误差的影响，将仿真及仿真数据进行优化处理，具体步骤如下：由车门结构可知，车门试验夹具模型有上铰链处夹具p1、下铰链处夹具p2、锁芯处夹具p3，结合传统车门模型与夹具的边界特性，分别释放被抑制的夹具p1、p2、p3得到模型1、模型2和模型3。

假设夹具模型整体误差为εM，车门上铰链夹具系统影响误差为e1，下铰链夹具系统影响误差为e2，锁芯处夹具系统影响误差为e3。通过Nastran计算出传统模型、模型1、模型2和模型3的仿真结果，如表2所示，可以看出，模型1、模型2的仿真结果与传统模型的输出结果相差都较小，模型3的仿真结果与传统模型的输出结果相差较大。

表2优化模型仿真分析结果

Tab.2 Simulated analysis results of optimization model mm

为获得各模型的敏感度，对比了夹具特征与工件接触部分的输出结果，详细数据见图8。

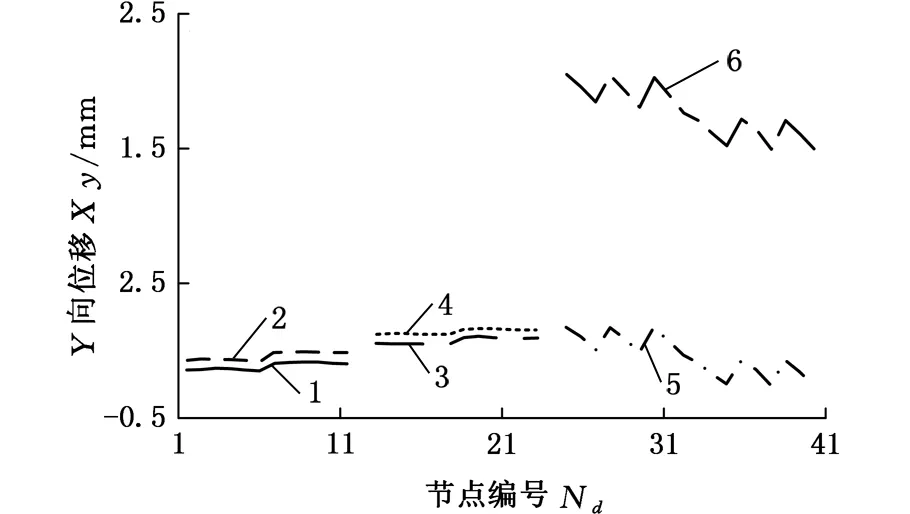
1.传统模型(上铰链) 2.模型1(上铰链)3.传统模型(下铰链) 4.模型2(下铰链)5.传统模型(锁芯) 6.模型3(锁芯)图8 传统模型与优化模型的接触面节点位移量Fig.8 Node displacement in traditional model andoptimization model

由图8看出，与传统模型相比，模型1和模型2的夹具接触面节点位移变化量较小，车门模型的刚度测量点处位移变化对模型1、模型2释放的夹具的灵敏度s可忽略不计，因此w1=w2=0，在模型优化过程中上下铰链处夹具仍然被抑制。

模型3的夹具接触面节点位移量较大，可见锁芯处夹具的影响较大，模型总体误差等于锁芯夹具系统影响的总体误差，即Ei=E0，所以w3=1，不能对其进行细节移除，因此，在模型优化过程中必须释放被抑制的锁芯处夹具。

由于试验测点数据不是测球表面的数据，而是测球中心的坐标，因此对车门的测点误差进行分析。首先根据有限元建模获得测点周围节点坐标(u、v的单位为mm)，拟合成曲面O，如图9所示，拟合方程为

S(u,v)=0.012 66u2+0.0122v2+0.002 188uv-
37.74u-23.86v+36 140

(26)

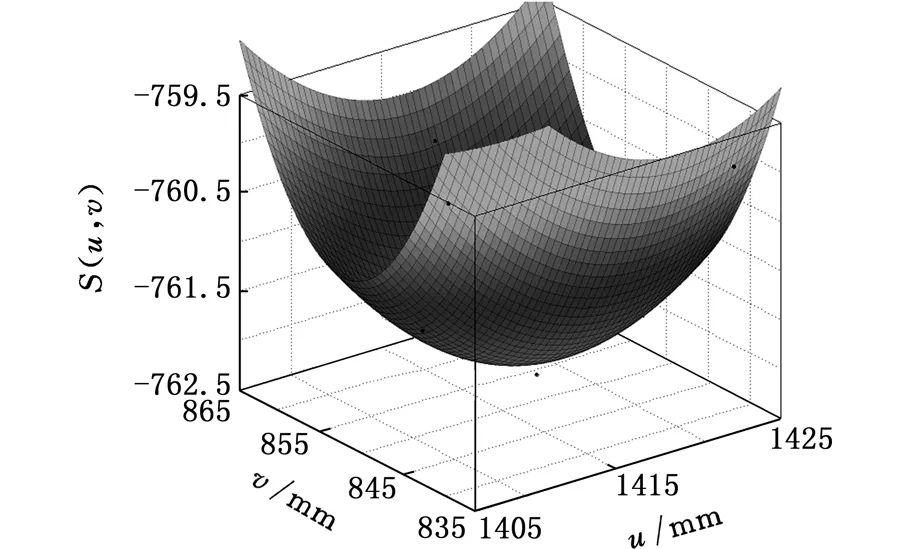
图9 拟合曲面OFig.9 Fitting surface O

然后对方程S(u，v)求偏导数得

(27)

求出曲面O中的各点的法矢量，向量的模为

(28)

车门刚度试验时,测球半径r=3 mm，代入测点中心数据(1415.62，855.082，-748.642)求得

n(u，v)=(-0.0259，0.1005)

(29)

优化夹具模型误差和测点误差后，得出了最终优化结果，见表3。

3.4 对比分析

修正试验后，上扭试验修正数据为4.207 mm，下扭试验修正数据为2.247 mm，忽略其他试验因素的影响，逼近真实值；因此上扭位移真实值近似为4.207 mm，下扭位移真实值近似为2.247 mm。

优化模型后，上扭分析数据为3.960 mm，下扭分析数据为2.150 mm。仿真数据接近真实值，验证了仿真模型的准确性；仿真结果与试验修正结果基本接近，验证了仿真和试验的准确性。

由表3可知，上扭相对误差从63.6%减小到了5.9%；下扭相对误差从64.7%减小到了4.3%。

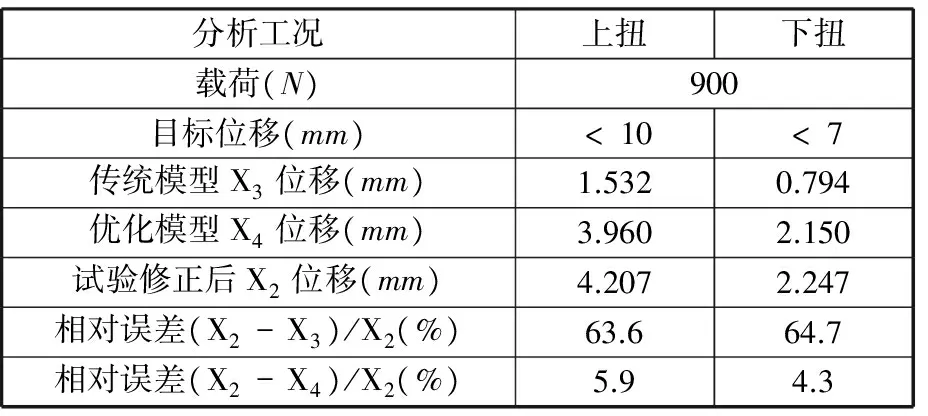
表3 前侧门优化前后的刚度

试验修正数据与仿真结果间的相对误差(表3)显著减小到6%。上下扭刚度各误差模型对整个车门刚度结果的相对误差分别为f1(Q,J,M,N)=(0.012，0.067，0.505，0.072)，f2(Q,J,M,N)=(0.034，0.113，0.527，0.077)。

4 结论

(1)提出了一种考虑夹具的车门刚度特性分析方法，建立了车门-夹具系统刚度的力学模型，准确模拟了试验过程。

(2)建立了试验误差模型和仿真误差模型，从试验和仿真两方面消除了试验数据采集误差、补偿试验柔性变形误差、修正传统模型误差和补偿测点误差。

(3)以某前门为例，通过对比试验与数值仿真，验证了误差模型的准确性，证明了夹具约束机构误差是试验数据与仿真结果产生偏差的主要原因。

[1] GOPALAKRISHNAN S H, SURESH K. A Formal Theory for Estimating Defeaturing-induced Engineering Analysis Errors[J]. Computer-Aided Design, 2007, 39: 60-68.

[2] LI Sansi, YANG Yingping, JIA Xinting, et al. The Impact and Compensation of Tilt Factors upon the Surface Measurement Error[J].Optik, 2016, 127:7367-7373.

[3] 唐建国，曹魏娟，高曙明.面向CAE的简化模型误差评估与信息重用[J].中国机械工程,2012,23 (8):961-966.

TANG Jianguo, CAO Weijuan, GAO Shuming. CAE Oriented Error Evaluation and Information Reuse of Simplified Models[J]. China Mechanical Engineering, 2012, 23(8): 961-966.

[4] MIHAYLOVA P, BALDANZINI N, PIERINI M. Potential Error Factors in 1D Beam FE Modeling for the Early Stage Vehicle Design [J]. Finite Elements in Analysis and Design,2013,74:53-66.

[5] AHMAD A, ANDERSSON K, SELLGREN U, et al. A Stiffness Modeling Methodology for Simulation-driven Design of Haptic Devices[J]. Engineering with Computers, 2014, 30(1): 25-141.

[6] ALLEMANG R. Conference Proceedings of the Society for Experimental Mechanics Series[M]//Effects of Errors in Finite Element Models on Component Modal Tests. Berlin：Springer, 2014：299-312.

[7] 乌春霞.汽车车门刚度的仿真分析与试验研究[D].长春：吉林大学，2007.

WU Chunxia. Simulation and Experiment Research of the Door Stiffness on Automotive[D]. Changchun: Jilin University，2007.

[8] 高云凯,徐成,方剑光，等. 汽车车身覆盖件刚度的试验研究[J].汽车工程，2013, 35(12):1117-1122.

GAO Yunkai, XU Cheng, FANG Jianguang, et al. An Experimental Study on the Stiffness of Automotive Closures[J]. Automobile Engineering, 2013, 35(12): 1117-1122.

[9] 陈永兴，吴晓燕，滕江川, 等. 基于误差传递建模的仿真可信性控制[J]. 计算机应用研究, 2013, 30(17): 1964-1966.

CHEN Yongxing, WU Xiaoyan, TENG Jiangchuan, et al. Simulation Credibility Control Based on Error Transfer Model[J]. Application Research of Computers, 2013, 30(17): 1964-1966.

[10] 王洋.三坐标测量机采样预测方法及测头补偿技术研究[D].沈阳：东北大学,2014.

WANG Yang. Prediction Sampling Method and Probe Compensation Technology of CMM Research [D]. Shenyang: Northeastern University, 2014.

[11] 林怡青，林秀君，彭美春,等.一种汽车ABS 试验台的等效惯量模型及误差分析[J].汽车技术,2005(9):24-27.

LIN Yiqing, LIN Xiujun, PENG Meichun, et al. An Equivalent Inertia Model of Automotive ABS Test Benches and Error Analysis[J]. Automobile Technology, 2005(9): 24-27.