架空输电线路导线覆冰厚度计算

李桂铭

(湖南电力建设监理咨询有限责任公司，长沙 410002)

0 引言

架空输电线路从低压到高压，乃至现在的超高压、特高压，经历了一个不断升压的过程。在电网电压等级不断升高的过程中，电网频繁受到了恶劣天气影响，发生大大小小的无数次电网事故，严重影响了电网安全运行。2008年的冰灾事故导致大面积停电和部分电网解列，使得湘赣、云贵、江浙等地电网出现不同程度的冰闪跳闸和断线倒塔。这些事故往往都伴随着恶劣的天气、困难的交通，加之停电导致通信中断，抢修难度大，严重时甚至会造成区域电网崩溃、长时间停电[1]，不仅给人们的生活带来极大不便，而且给电网的建设、维护带来极大的经济损失。鉴于此，本文对导线覆冰的力学模型进行论述分析，并结合分析出的覆冰数据和在线监测系统所测数据对湖南地区已运行线路的抗冰、防护进行研究分析，从而为湖南电网的抗冰工作提供参考。

1 覆冰对输电线路力学特性的影响

通常情况下，随着覆冰量的增加，输电线路中承担主要输电任务的导线所受垂直荷载将会逐步倍增，从而使得导线拉伸变长、弧垂增大，导线对地距离及交叉跨越间距减小，当覆冰达到一定量后，将会引起电网发生闪络事故。另外，导线覆冰弧垂增大的同时，受风载荷的影响发生风偏，使得原先拥有安全距离的相导线间、导地线间出现放电，甚至发生相碰，从而造成短路跳闸，烧伤、烧断导线等各类事故，经过调查研究、分析，主要有以下几种情况[2]。

(1)架空导、地线因覆冰过载，垂直荷载过大，超过原有基础设计承载力，基础出现不同程度的下沉、倾斜或爆裂，进而破坏基础，引起塔身倾斜或者杆塔倾倒。

(2)随着覆冰程度加重，架空导、地线所受附加荷载逐步增大，达到一定程度后，将会发生导、地线直接从接头处压接管内抽出的事故，导线外层铝股被压接管口切断，钢芯抽出的事故，耐张线夹出口附近导线外层若干股被切断或整根导、地线直接拉断的事故。

(3)因一侧导、地线覆冰过载突然断开，使得输电杆塔的杆头单侧受力，引发顺线路方向杆塔头部折断的事故；或者原本平衡对称布置导、地线的杆塔，因导、地线相线间覆冰程度不同而形成不对称，引发垂直线路方向杆塔头部折断的事故。

(4)因导、地线覆冰后弧垂增大，导线对地距离及交叉跨越间距减小，从而引发输电线路发生闪络事故；或者导、地线弧垂增大后，因不同程度的风偏、舞动作用，使得导、地线放电或互碰，引发烧伤和烧断导、地线的事故。

(5)因导、地线覆冰过载，造成悬垂线夹船体受损，通常会在U型螺丝附近发生断裂，从而引发事故；另外，拉线电杆也会因为线路覆冰受到不均衡的作用力，导致拉线楔形线夹断裂，从而引发倒杆事故。

(6)因输电线路导线间覆冰不均匀，容易导致多分裂导线出现扭转，当覆冰达到一定程度时，导地线出现不同频率的脱冰跳跃，从而引发绝缘子串翻转、碰撞、炸裂等事故。

2 导线覆冰厚度模型及实例分析

2.1 导线覆冰厚度模型

目前，研究、应用较为广泛的是在输电线路上安装在线监测装置，对运行线路的运行状态、周边气候环境条件等进行监测，通过监测记录导、地线覆冰，导线舞动，导线及金具受力变化情况等相关数据资料，对输电线路的运行进行校验和预测。

理论模型：主杆塔的等效挡距假设为图1，将主杆塔绝缘子串上竖直方向的张力Fv与两侧导线某点到主杆塔A点间导线上竖直方向荷载相互平衡的点定义为平衡点[3]。

图1 主杆塔等效挡距示意

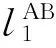
悬点不等高情况下导线长度近似计算公式[4]

(1)

式中：L为悬点不等高导线近似长度，m；l为挡距(两悬挂点之间水平距离)，m；h为高差(两悬挂点之间垂直距离)，m；q0为导线自重载荷集度，N/m；Fh为导线最低点的水平拉力，N。

利用公式(1)推导得出导线最低点水平拉力计算公式

(2)

代入现场数据，即可解出导线最低点水平拉力Fh。

悬点不等高情况下等效挡距计算公式[5]

(3)

式中：h为主杆塔与单侧副杆塔悬挂点的高度差，若主杆塔较高，则h为正值，否则为负。

式(3)中：

用L1表示等效挡距为l1时导线的长度[6]，则

(4)

考虑到主杆塔上绝缘子串均存在一定的倾斜角(设定为θ)，使得主杆塔两侧导线上的水平拉力分量可能不同，但由水平方向力的平衡可得出

FhAB=FhAC+Fvtanθ，

(5)

式中：FhAB，FhAC分别为AB，AC段导线在主杆塔悬挂点的水平拉力分量，N。

利用式(5)所得结论，对式(4)进行推导可得主杆塔两侧导线长度L1AB，L1AC分别为

(6)

根据理论模型所建立的平衡点，风载荷集度设定为qw，覆冰载荷集度设定为qi，则同时有冰、风载荷共同作用时与只有自重载荷作用时杆塔上竖向载荷的差值ΔFv表示为

(7)

式中：qm为风、覆冰的综合载荷集度，qm=qi+qw，将式(7)进行推导可得

(8)

覆冰载荷集度

qi=qm-qw，

(9)

其中:风载荷集度qw可以通过风速传感器、导线直径和风夹角等算出；杆塔上竖向载荷的差值ΔFv可以通过拉力传感器测量、计算出。

结合覆冰的密度、导线直径等已知条件，利用导线覆冰标准冰厚公式(10)，即可测算求得具体覆冰的厚度。式(10)为电力系统线路设计导线覆冰标准冰厚公式，前提是假定覆冰形状为均匀的圆柱体(如图2所示)。

(10)

式中：b为覆冰厚度；γ0为覆冰密度；d为导线的计算等效直径。

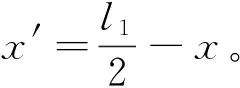
该点距弧垂最低点O的垂直高度为

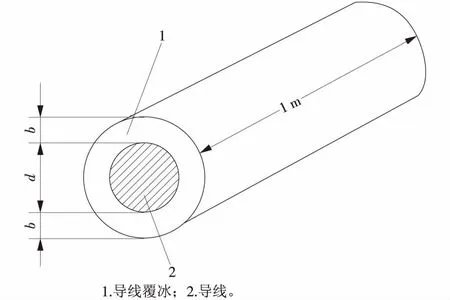
图2 覆冰导线结构

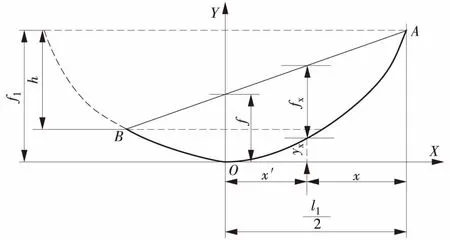
图3 导线弧垂计算模型

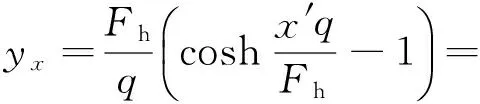
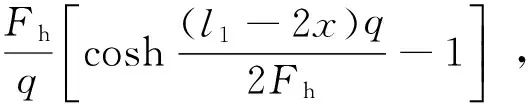
(11)

则该点的弧垂fx为

(12)

最低点弧垂f为

(13)

式中：q为导线自重及风、覆冰综合作用下垂直载荷集度，q=q0+qi+qw=q0+qm，N/m。

2.2 算例分析

以湖南省±800 kV复奉线#1086～#1087段导线为例，计算2016年1月26日现场气候环境条件下的导线覆冰厚度。该线路采取耐张塔，导线的相关参数见表1。

设已知气象条件下的温度为tm、比载为gm、应力为σm，令待求气象条件下的温度为tn、比载为gn、应力为σn，则状态方程为

(14)

式中：α为导线热膨胀系数；β为导线的弹性伸长系数，154×10-5mm2/N；l为挡距。

代表挡距为448 m，查阅导线安装曲线中得温度为-5 ℃、风速10 m/s时的应力σm=46.40 MPa，求得风速为10 m/s、温度为-15 ℃时导线的应力σn=46.65 MPa。

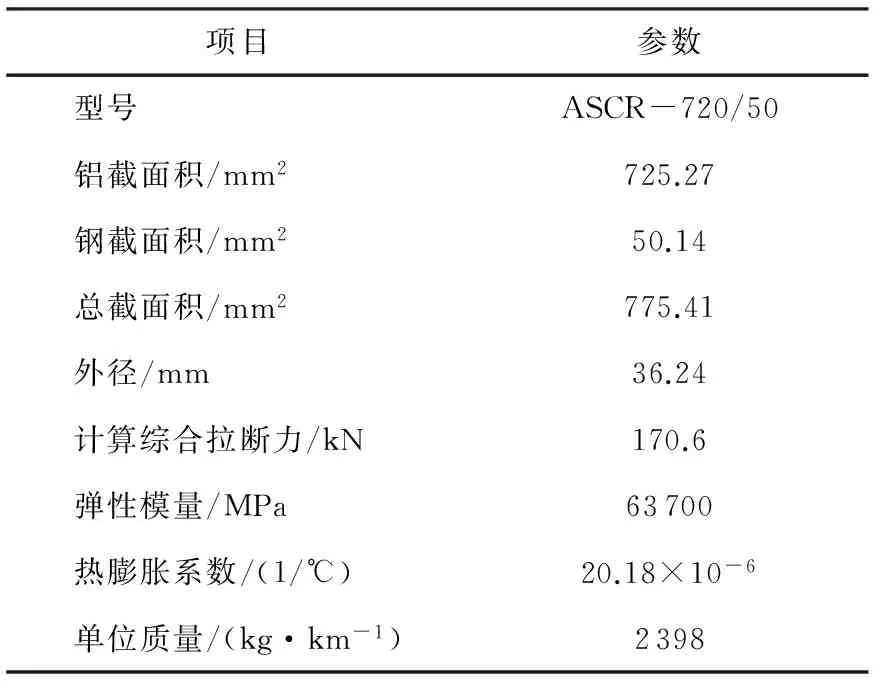
表1 导线参数

导线张力为36 910 N ，6分裂导线所受张力=6×36 910×10-3≈222 (kN)，因±800 kV耐张绝缘子串为三联成串，则卡具额定荷载为74 kN，安全系数为2.5。

设覆冰时温度为t，水平应力为σ0，垂直总比载为γ。原始挡距为l，由悬垂串偏斜量得到的挡距改变量为Δl，高差角为β。测量得到此时的弧垂为f，根据弧垂公式有

(15)

从上式可知，已知弧垂只能求得比载与水平应力的比值，要想得到比载γ，需要求得σ0。线路在覆冰状态和正常运行状态下的参数满足下面的状态方程

αEcosβ(t-t1) ，

(16)

式中：α，E分别为导地线的温度膨胀系数和弹性系数；下标1的各量为线路正常运行状态1时的参数，是已知的。

联立式(15)，(16)可以得到覆冰时的垂直总比载γ，减去导线自重比载g0(已知)，可得覆冰比载γi，再根据覆冰载荷集度qi与覆冰比载γi、覆冰截面积间的关系求得此时的等值覆冰厚度。

(17)

通过计算得到±800 kV复奉线#1086～#1087段导线2016年1月26日计算覆冰厚度为1.82 mm，通过现场观冰测站实测得到实际覆冰厚度为2.00 mm，相对计算误差为9.02%，在10.00%以内。

3 结论

(1)通过建立导线覆冰厚度的力学模型，分析出了导线覆冰后的弧垂计算公式。

(2)根据力学模型，计算出了湖南±800 kV复奉线#1086～#1087段导线的覆冰厚度，为导线防覆冰提供了理论基础。

(3)导线覆冰力学计算结果与实测结果相对计算误差为9.02%，在10.00%以内，证明了力学计算结果能够很好地验证导线覆冰厚度，可为提前预测导线覆冰厚度提供参考，还可为导线覆冰防护提供预警。

[1]蒋兴良,易辉.输电线路覆冰及防护[M].北京:中国电力出版社,2002.

[2]戚大安.电网覆冰灾害的特点和发展趋势[J].电业政策研究，2007,1(1):27-30.

[3]张弦.重冰区线路导线过载冰设计计算[J].电力勘测设计，2005,8(4):64-67.

[4]唐春林.覆冰过载情况下电线的允许比载和冰厚计算[J].华东交通大学学报,2006,23(1):102-105.

[5]朱宽军,刘超群,任西春.架空输电线路舞动时导线动态张力分析[J].中国电力,2005,38(10):40-44.

[6]张宏志.大面积导线覆冰舞动事故的调查与分析[J].东北电力技术,2001(12):15-19,43.