基于自适应加速因子粒子群优化算法的裁剪分床研究
2018-02-05,,
,,
(浙江工业大学 信息工程学院,杭州 310000)
0 引言
服装行业的裁剪优化分床问题是根据企业的生产条件和相应订单情况,将订单中的号型种类、数量和颜色进行合理搭配,科学的安排裁剪床数、铺布层数和套排规格件数[1],使得分床床数达到最少、布料消耗达到最低、生产效率达到最高、裁剪数量误差最小的优化组合问题[2]。裁剪优化分床一直是制约服装行业提高生产效率、节约布料的难题,同样也出现在箱包、家居、鞋帽等行业中。同时,劳动力成本的提升以及服装材料价格提高,使得服装生产成本越来越高。因此,通过优化分配以减少分床数量和裁剪误差,从而减少人工工作量,提高原材料的利用率,降低生产成本,能够产生巨大的经济效益,具有重大的现实意义[3]。
传统的数学思维分床方法具有一定的规范性,但是效率比较低,分床结果误差比较大,仍然得不到比较理想的分床方案。但相比于人工分床的效率有显著提高,且分床结果误差可显著减少。传统的数学思维分床方法主要有分组法、加减法、并床法、比例法[4-5]、取半法[6]、等量优化分床法[7]、试凑法等。这些方法对生产订单的数据要求较高,各号型样片数量之间必须具备某种特定的关系,具有一定的局限性,只适用于一些特定的订单,并不适用于实际的分床订单[7-8]。
因此,为了解决目前在裁剪分床领域遇到的这一难题,本文引入现代智能优化算法,在经典粒子群优化算法(particle swarm optimization,PSO)的基础上,设计一种基于自适应加速因子粒子群优化算法(SAPSO)的裁剪分床方法。利用SAPSO算法的简单易实现、参数个数少、收敛速度快等特点,以各号型样片裁剪数量误差平方和为目标,建立裁剪优化分配求解的数学模型。最后,通过分床实例验证了该方法的有效性。
1 裁剪分床的数学模型
服装裁剪分床是根据生产订单要求和企业生产条件,将生产订单中各号型样片件数、颜色进行合理的组合搭配,科学地制定出裁剪分床床数、各床铺布层数、各号型套排的配比,并降低布料损耗、减少工时消耗、提高生产效率的工艺设计过程,俗称分床。裁剪分床主要包括以下几个方面:(1)生产订单裁剪分床床数。裁剪分床床数决定了裁剪工时的消耗;(2)每床需要铺的号型种类,每个号型铺布的件数。在生产条件允许的范围内,套排号型种类越多越节约原材料;(3)每床需要铺布料的层数。在生产条件允许的铺布层数范围内,铺布层数越大,裁剪的效率就会越高。由于在同一床里具有不同号型,不同号型套排的件数也不一样,因此需要进行合理的优化搭配。
设某服装生产订单有m种号型,每种号型的裁剪数量为Di(i=1,2,...,m)、每种号型允许的最大裁剪误差数量ρ,裁床的铺布层数Cnt的上限Cntmax和下限Cntmin,各号型样片在每床上配比Pb的上限Pbmax,最佳的分床床数t。因此,裁剪分床求解的数学模型为:
(1)
约束条件为:
(2)
其中:Ai表示第i种号型样片实际裁剪的件数,Pbij表示第i种号型样片在第j床上套排的件数,Cntj表示第j床上的铺布层数,εi表示第i种号型的裁剪误差件数,Fvalue表示各号型样片实际裁剪件数与目标裁剪件数之差的平方和。裁剪分床是在满足约束条件的前提下,求解使目标Fvalue最小的铺布层数Cntj和对应的配比Pbij。将上式表示成矩阵的形式:
A=Pb×Cnt
(3)
ε=A-D
(4)
A是各号型样片实际裁剪数量矩阵;Pb是各号型样片在各床上套排的件数组成的矩阵,也称配比矩阵,其中每一行表示某种号型样片在各床上套排的件数;Cnt是各床铺布层数的矩阵;ε是各号型样片裁剪数量的误差矩阵。
2 SAPSO算法的设计与实现
2.1 算法选择
由于本模型是非线性的,采用常规的解析法无法进行求解,因此引入现代智能优化算法。现代智能优化算法很多,但是其中很多算法参数比较多,复杂度较大,实现起来比较难。而粒子群优化算法比较简单,参数较少,收敛速度快,实现起来比较容易,再结合本模型及裁剪分床的实际情况,优先选择粒子群优化算法进行求解。
2.1.1 PSO算法
经典粒子群优化算法(PSO)是由Kennedy和Eberhart于1995年提出的一种种群优化算法[9-11],PSO算法具有概念简单、实现容易、精度高、收敛速度快和需要调整的参数少等优点,是一种启发式算法[12-13]。该算法可表述如下:在K维的搜索空间ΩK内,种群的大小M(即粒子的数量),种群中第i个粒子的位置值αi={α1,α2,…,αM},速度向量值vi={v1,v2,…,vM},其中粒子的历史最好位置Pbesti={Pbest1,Pbest2,…,PbestM},当前整个种群的全局最好位置Gbest。每个粒子的速度向量值和位置向量值的更新公式分别为:
(5)
(6)

2.1.2 SAPSO算法
针对经典粒子群优化算法求解离散优化问题容易陷入局部最优的问题[14],在经典粒子群优化算法中引入自适应加速因子,设计了一种基于自适应加速因子粒子群优化算法。其中自适应加速因子与算法迭代次数成反比关系,迭代次数越大,自适应加速因子越小。因此在算法搜索的前期,自适应加速因子较大,算法的全局搜索能力较强,在算法搜索的后期,自适应加速因子较小,算法的局部搜索能力较强,收敛速度更快,搜索效率更高。自适应加速因子粒子群优化算法(SAPSO)的速度和位置更新公式分别为:
(7)
(8)
自适应加速因子为:
(9)
其中:γ为正整数,n为当前迭代次数,N为最大迭代次数。
2.2 裁剪分床方案设计
本文采用SAPSO算法进行裁剪分床方案的设计,其实现过程如图1裁剪分床实现流程图所示。

图1 裁剪分床实现流程图
第一步,设定裁剪分床过程中的初始条件,其中包括裁剪分床限制条件和SAPSO算法参数;第二步,根据各号型所要裁剪的总件数、每床铺布层数的上限和下限、每层布可裁剪服装号型样片件数上限和下限来计算可能的分床床数;第三步,采用SAPSO算法搜索各床上的铺布层数:以各床上的铺布层数作为粒子的位置,给各床在搜索空间内随机初始化一个层数,同理初始化速度值,将第一个粒子的位置当做局部最优和全局最优的初始值,并且将初始适应值设置为正无穷大;第四步,再采用SAPSO算法搜索在对应铺布层数下,使配比粒子适应值最小的配比;第五步,根据当前铺布层数及对应的局部最优值和全局最优值,更新铺布层数粒子的速度值和位置值,再计算铺布层数更新后的适应值,以更新铺布层数粒子的局部最优值和全局最优值;第六步,若迭代次数达到设定值,则以最终搜索的各床铺布层数和各号型在各床上最优配比作为分床方案,否则转到第四步继续搜索。
2.3 SAPSO算法实现
1)首先由用户根据实际的生产条件设定每床铺布层数Cnt的上限Cntmax和下限Cntmin,每层布可裁剪样片总件数T的上限Tmax和下限Tmin,每种号型样片每床排的件数Pb的上限Pbmax,各号型样片所需裁剪的件数Si;自适应加速因子正整数参数γ,认知因子c1,社会因子c2,算法迭代过程中层数粒子速度向量的最大限幅Vcmax、配比粒子速度向量的最大限幅Vbmax。
2)然后根据各号型样片所需裁剪的件数计算出各号型样片所需裁剪的数量总和:
(10)
平均每床铺布层数:
(11)
平均每层布裁剪的件数:
(12)
根据以上结果计算出所需分床数量Bedi的上限:
(13)
所需的分床数量下限:
(14)
其中:ceil和floor分别表示向上取整和向下取整。
3)由于计算出来的分床床数Bed是在一个有限的范围内,所以先搜索床数小的分床方案,如果床数小的方案不符合要求,再去搜索床数大的分床方案。在某一分床床数情况下,采用SAPSO算法搜索铺布层数,其算法搜索过程如图2所示。

图2 铺布层数粒子搜索流程图
4)以各床上的铺布层数作为粒子的位置,给各床在搜索空间ΩK(铺布层数限制范围)内随机初始化一个层数,同理初始化M个粒子{Cnt1,Cnt2,…,CntM},以及速度向量值{v1,v2,…,vM},以各号型样片误差平方和为适应值Fvalue。令各个粒子的初始个体历史最优Pbesti=Cnti,粒子的全局最优Gbest=Cnt1。
5)再采用SAPSO算法搜索在对应铺布层数下,使Fvalue最小的配比Pb:其搜索过程如图3所示。

图3 配比粒子搜索流程图
(1)将第j种号型样片在各床上的配比作为粒子的位置Pbi,在搜索空间ΨK(配比的限制范围)内,给该号型样片在各床上的配比随机初始化一个值,同理初始化M个粒子{Pb1,Pb2,…,PbM},速度向量值{vb1,vb2,…,vbM}。令各个粒子的个体历史最优Pbest1i=Pbi,粒子的全局最优Gbest1i=ceil(Pb1)。(2)根据配比粒子速度更新公式:
(15)

(16)
Fvalue1i=[ceil(Pbi)×Cnti-Dj]2
(17)
通过比较前后两次适应值的大小来更新粒子的历史最优配比Pbest1i,以及全局最优配比Gbest1j。(5)迭代次数n1=n1+1,若迭代次数达到设定值N1,给出所有号型样片对应铺布层数下的最优配比Gbest1j,结束搜索;否则转到步骤(2)继续搜索。同理搜索其他号型样片在各床上的配比。
6)再根据铺布层数粒子的速度更新公式:
(18)

7)再根据位置更新公式:
(19)
8)然后计算所有粒子的适应值Fvaluei:

(20)
通过比较前后两次适应值的大小来更新局部最优Pbesti和全局最优Gbest。
9)迭代次数n=n+1,若迭代次数达到设定值N,则输出所有号型样片最优的铺布层数Gbest和对应的所有号型样片的最优配比Gbest1,结束搜索;否则转到步骤5)继续搜索。
3 实验结果与性能分析
本实验的配置环境:硬件配置为Intel Core i3-2310M,CPU主频为2.40 GHz,4 GB内存;软件环境:64位Windows7操作系统,安装Microsoft Visual C++ 2013软件开发平台。本方法选择一个包含6种号型和一个包含5种号型的实际生产订单进行实验分析。通过与等量优化分床法分床结果进行对比分析,在分床结果误差和用料预算上进行比较,对SAPSO算法的性能进行测试,两者分别针对相同的生产订单进行分床实验;与经典PSO算法进行分床效率的比较。SAPSO算法分床过程中两次的设置参数相同,算法参数设置如下:最大迭代次数N=N1=100,自适应加速因子中正整数参数γ=100,认知因子c1和社会因子c2都取值2,种群大小为M=20。算法迭代过程中层数粒子速度向量的最大限度Vcmax=20、配比粒子速度向量的最大限幅Vbmax=2。分别对两个订单进行分床,两种方法的分床结果如图4和图5所示。

图4 订单一两种方法的分床结果
图4为6种号型订单两种方法的分床结果,其中(a)为等量优化分床法结果,(b)为SAPSO算法分床结果;图5为5种号型订单两种方法的分床结果,其中(a)为等量优化分床法结果,(b)为SAPSO算法分床结果。对比两种分床方法的结果,在相同的约束条件与相同的生产订单情况下,采用SAPSO算法进行分床的结果明显比等量优化分床法分床结果误差小;在用料预算上,SAPSO算法分床结果比等量优化分床法用料预算更少,更节省原材料。虽然在用料预算上提高的不多,但对于订单量上亿的大型企业来说带来的经济效益也是不容忽视的。
图6为经典PSO算法与SAPSO算法的适应度曲线,从两者的适应度曲线可以看出,SAPSO算法分床在迭代23次左右搜索到最优解,PSO算法分床在迭代52次左右搜索到最优解,从图6中可以看出SAPSO算法收敛性比PSO算法更快,分床效率更高。

图5 订单二两种方法的分床结果
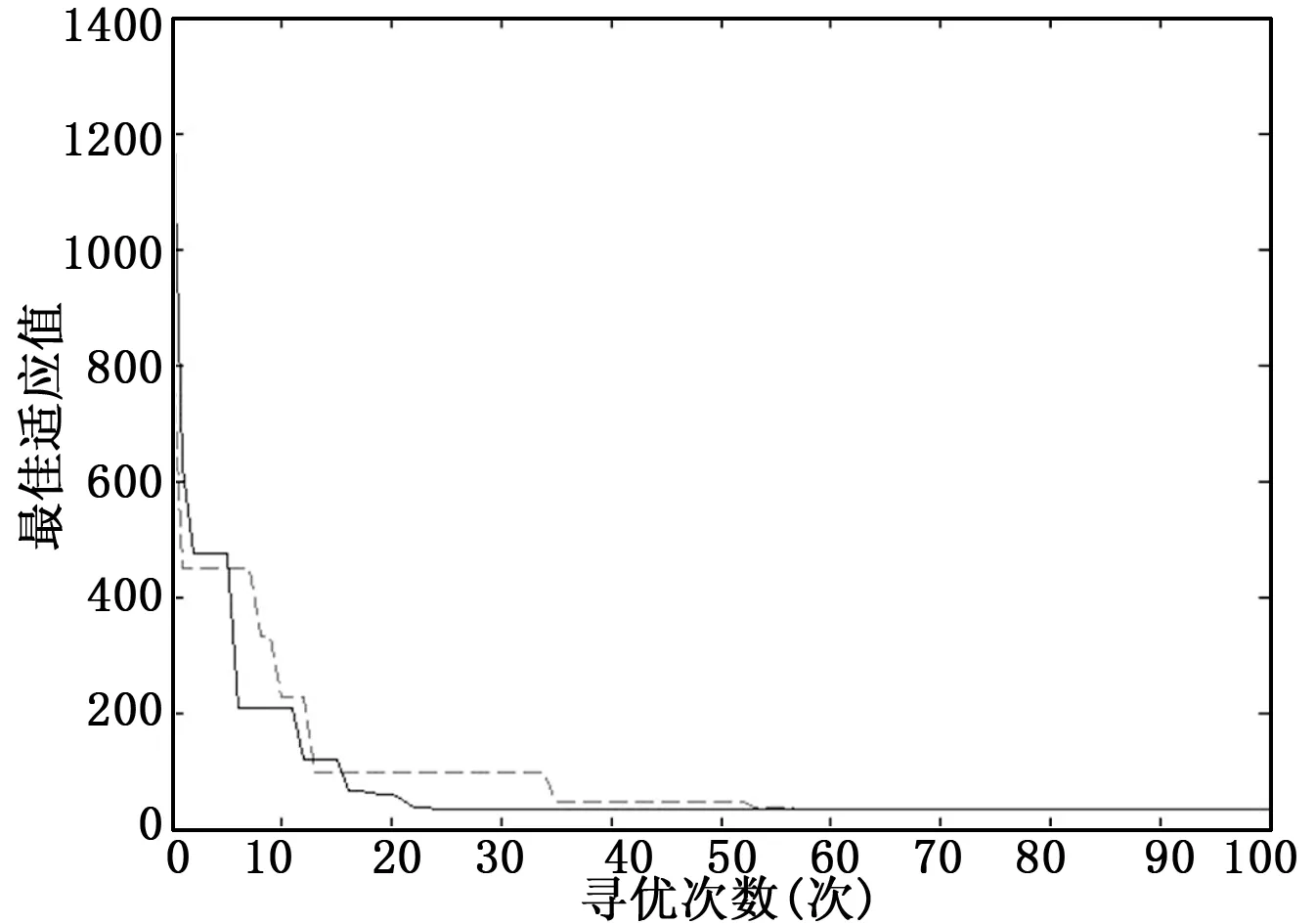
图6 PSO与SAPSO算法适应度曲线(实线—SAPSO,虚线—PSO)
4 结论
本文设计的基于SAPSO算法裁剪分床的方法,通过将裁剪分床的铺布层数和各号型在各床上的配比抽象成SAPSO算法中的粒子进行搜索,有效地减小裁剪误差,从而提高原材料的利用率,给服装行业的裁剪分床问题提供了一种新的解决方法。该方法简单易行,需要调整的参数少,且收敛速度快。实验结果表明SAPSO算法分床的误差比等量优化分床法小,并且在用料预算上SAPSO算法分床更少,更节约原材料。SAPSO算法收敛速度比PSO算法快、耗费时间短,效率更高。
[1] 刘艳梅, 颜少聪, 纪杨建,等. 大批量定制服装裁剪分床计划的两阶段优化方法[J]. 计算机集成制造系统, 2012,18(3):479-485.
[2] 刘吉庆. 制订裁剪分配方案的研究[J]. 包装世界, 2009(4):108-110.
[3] 庹 武, 郑 攀, 常亭亭, 等. 基于层次分析法的服装裁剪分床影响因素[J]. 纺织学报, 2013,34(4):148-152.
[4] 师 华, 戴 鸿. 服装企业裁剪分床案例分析与探讨[J]. 山东纺织经济, 2008(5):117-118.
[5] Degraeve Z, Gochet W, Jans R. Alternative formulations for a layout problem in the fashion industry[J]. European Journal of Operational Research, 2002,143(1):80-93.
[6] 姜 蕾. 服装生产工艺与设备[M]. 北京:中国纺织出版社, 2004.
[7] 郑 攀, 庹 武. 服装裁剪自动分床系统的研究与开发[J]. 山东纺织经济, 2013,(11):76-79.
[8] 王晓云, 黄珍珍, 张洪志, 等. 服装裁剪工艺计划优化系统的开发研究[J]. 价值工程, 2010,29(5):187-188.
[9] 李明阳, 严 华. 改进粒子群算法在云计算负载均衡中的应用研究[J]. 计算机测量与控制, 2016,24(10):219-221.
[10] 潘 峰. 粒子群优化算法与多目标优化[M]. 北京:北京理工大学出版社, 2013.
[11] Kennedy J, Eberhart R. Particle swarm optimization[A]. IEEE International Conference on Neural Networks, Proceedings[C]. IEEE, 1995(4):1942-1948.
[12] 程 跃, 程文明, 郑 严. 基于改进粒子群算法的中药提取过程PID优化控制[J]. 计算机测量与控制, 2010,18(3):533-534.
[13] Ma L, Forouraghi B. A Modified Particle Swarm Optimizer. Advances in Natural Computation[M]. Springer Berlin Heidelberg, 2012.
[14] 赵鸿图, 刘 云. 改进粒子群算法的小波神经网络语音去噪[J]. 计算机测量与控制, 2013,21(10):2799-2800.
