反导火力单元空间杀伤区内拦截概率研究
2018-02-05,,,
,, ,
(1.解放军装备学院 研究生三队,北京 101416; 2.解放军装备学院 航天指挥系,北京 101416 )
0 引言
弹道导弹的飞速发展,使得未来的空天安全面临着极大挑战。反导作战成为未来战争的重要形式之一,中段反导具有拦截次数多、实施拦截早、附带伤害少等特点[1],所以中段反导作战在导弹防御中有着至关重要的作用。反导火力单元的部署问题是进行反导作战的前提,对于火力单元部署问题就是使得以最少的部署成本获得尽可能高的拦截概率,所以火力单元在空间中杀伤区内任意理论拦截点的拦截概率成为部署问题的前提。
目前利用拦截弹与目标直接碰撞产生的巨大动能来毁伤目标,是主要的反导方式之一[2]。为了达到碰撞杀伤的效果,必须将拦截弹的零控脱靶量控制在一定的精度范围内。本文以末制导初始时刻的零控脱靶量为评价策略,即在末制导初始时刻的当零控脱靶量小于在该时刻的末制导的修正能力时,拦截弹能够修正误差进行成功拦截。本文通过分析某一中段反导武器的杀伤区,选取不同高度和位置的理论拦截点进行拦截仿真,完成了针对火力单元在空间杀伤区内任一点的拦截概率的计算。
1 拦截弹数学模型
1.1 拦截弹在空间中的杀伤区
选取一典型的中段反导武器其发动机大致参数如表1所示[3-4]。
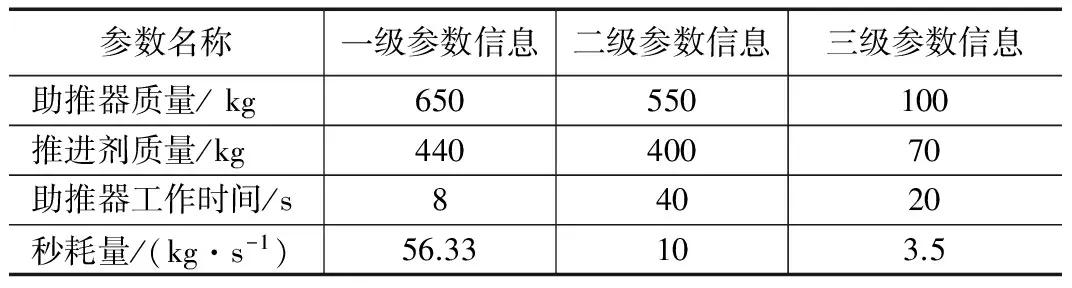
表1 拦截弹发动机大致参数
该中段反导武器在其第三级关机后[5],直到其下降段之前的范围内可以进行拦截,当来袭导弹的弹道轨迹进入该包络面时认为可以对其进行拦截。本文采用的地球模型为标准的球形,由于拦截弹飞行时间比较少,并且考虑到中段反导武器可能的部署位置,在纬度较高的地区科式力的影响相对较小,本文中采取简化的模型,认为火力单元在空间中,朝着任意方位发射杀伤区的范围都相同,所以火力单元在空间中的杀伤区域在任意朝向的轨迹相同。碰撞拦截分为顺轨拦截和逆轨拦截,本文仅分析逆轨拦截情况,即火力单元必须部署在拦截点的前面,故将拦截弹在180°范围内在空间中的可达集作为其在空间的三维杀伤区范围。选取的该拦截弹在空间中杀伤区如图1所示。

图1 拦截弹在空间中的杀伤区
图1中火力单元部署在原点O位置,拦截的来袭导弹的方向为沿着y轴的负方向。杀伤区由4个曲面和一个平面组合而成,具有良好的轴对称性。可以看出其最远射程可以达到450 km左右,拦截高度可以达到430 km左右。
当来袭导弹进入火力单元的杀伤区时,认为火力单元可以对来袭目标进行拦截。单次动能中段反导拦截过程最终发生在杀伤区内的一个小区域范围内,或者说发生在预测命中点附近。在进行拦截效能评估之前,首先要解决的问题是在火力单元杀伤区范围内任意预测命中点的拦截概率值。
1.2 拦截概率计算模型
中段反导发生在大气层外,预测命中点的拦截概率与脱靶量有密切的关系。终端脱靶量是由零脱靶量初始误差和拦截器的修正能力共同决定[6]。本文中假设来袭目标在中段不进行机动,当拦截器导引头捕获目标时,拦截器采用理想比例导引的方式进行修正。
在末制导的初始时刻的脱靶量为:
(1)
其中:vf(t)服从(mv,σv)正态分布,r(t)服从(mr,σr)正态分布,vIA服从(mV,σV)的正态分布。vf为相对速度在视线法向的投影,r为相对距离[7]。即该方程可以表示为脱靶量由来袭导弹和拦截弹的视线法向的相对速度在剩余拦截时间段内运动的距离。ρf的均值mρf和标准差σρf可采用Rosenbulth法[8]近似计算得到。
考虑到脱靶量近似的服从高斯分布,则其概率密度分布函数可以表示为:
(2)
在拦截弹捕获目标的时刻,拦截弹的末制导修正能力为ZI。则拦截弹对目标成功拦截的概率可以表示为:
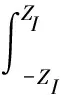
(3)
利用标准高斯分布计算公式为:
(4)

1.3 拦截弹末段修正能力分析
考虑到末制导拦截时间较短,本文采用简化的相对运动模型,假设拦截弹和来袭导弹在末制导段的相对运动为平面内的匀速直线运动,其运动过程可以表示为如图2所示。

图2 拦截弹和来袭弹的相对运动模型
则末制导段相对运动时间为:
(5)
式中,rg为拦截弹捕获目标时,弹目的相对距离。VI和VA为该时刻拦截弹和来袭弹的速度。
本文选取的拦截弹参照SM-3拦截弹,动能战斗部是MK142,在文献[9]中给出SM-3拦截弹的比冲范围是260~265 s,Leap的质量大约重16.7 kg,推进剂4.5 kg,Leap能够实现的加速度为6 g具体参数如表2所示。

表2 拦截弹相关参数
燃料的燃烧时间可由装药质量(即推进剂质量)和燃料每秒的消耗量来表示:
(6)

(7)
其中,FA为平均推力。
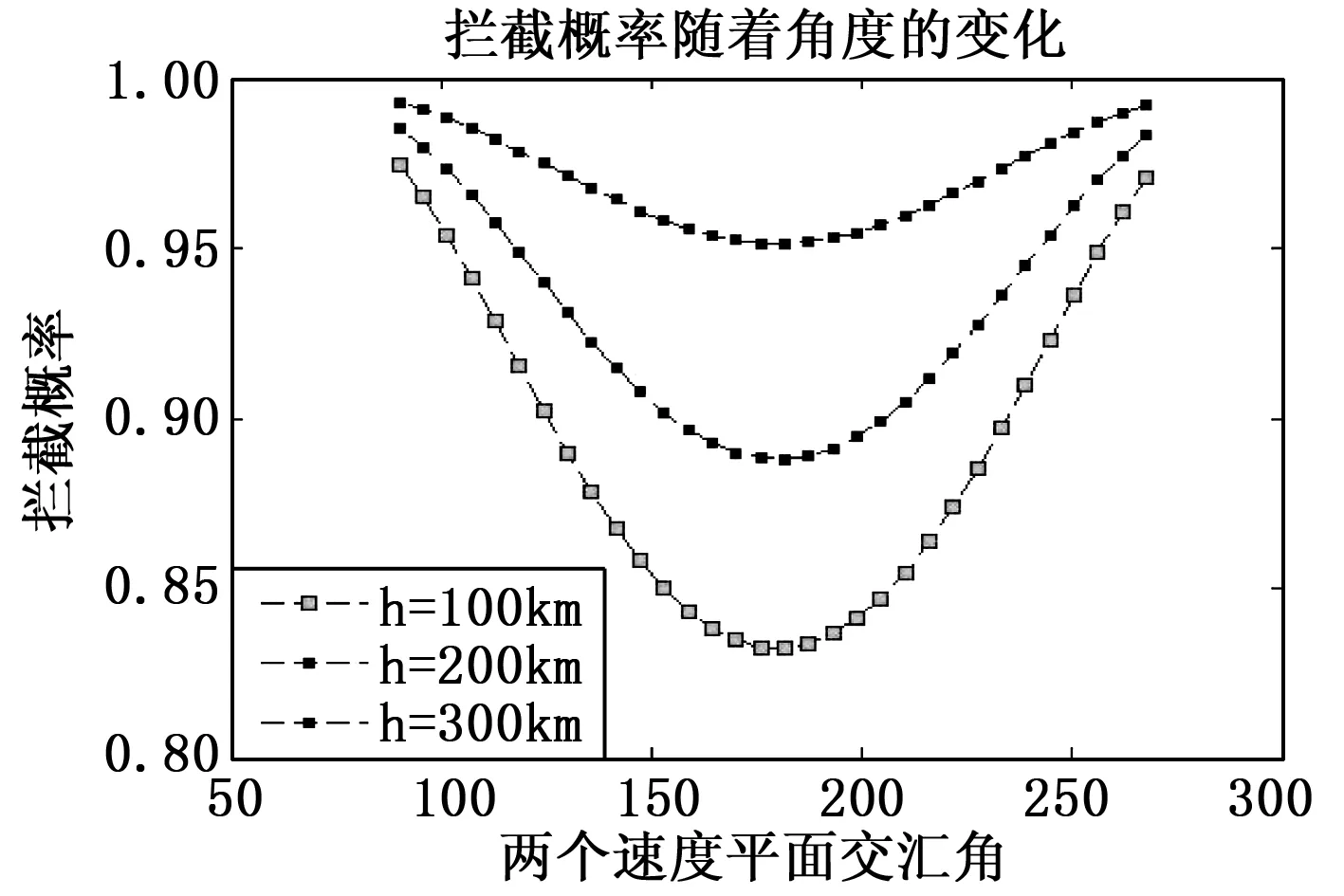
文中选取主要参数如下:比冲280 s,机动加速度为5 g。 当末制导段相对运动时间小于燃烧时间,即tg (8) 当末制导相对运动时间大于燃烧时间时,即tg>tr时,末制导修正能力为: (9) 拦截弹碰撞拦截来袭导弹的过程发生在理论拦截点附近。在来袭导弹的理论拦截点建立一个坐标系,用一个球心与地心重合,理论拦截点到地心的距离长度作为半径的均匀球面与理论拦截点相交。 坐标系的定义与北东坐标系类似,坐标系的坐标原点位于理论拦截点,x轴方向在理论拦截点水平面内指向正北方向,y轴方向为过理论拦截点的地心矢径指向上方,z轴方向由右手定则确定。该坐标系可以称之为拦截坐标系。如图3所示 图3 拦截坐标系示意图 图中h为理论拦截点的高度,OA为来袭导弹的发射点,T为来袭导弹的落点。假设理论拦截点所在的球面上的经度为CL,纬度为BL。 来袭导弹在理论拦截点的位置矢量为TA=(xa,ya,za)则拦截点的经纬度可以用向量夹角求得。地心坐标系的Z轴方向矢量表示为Z=(0,0,1),则理论拦截点的纬度为: (10) 来袭导弹在理论拦截点的位置矢量,在地心坐标系xy平面的投影为TAxy=(xa,ya,0),地心坐标系的X轴方向矢量表示为X=(1,0,0)则理论拦截点的经度为: (11) 地心坐标系到拦截坐标系的关系如图4为: 图4 地心坐标系到拦截坐标系转换关系 地心坐标系到拦截坐标系的转换矩阵,可以由地心坐标系经三次基元转动而成[10], LEL=M2(-π/2)M1(BL)M3(-π/2+CL) (12) M3(ξ)表示绕z轴逆时针旋转ξ角度值,表示为: (13) M2(η)表示绕y轴逆时针旋转η角度值,表示为: (14) M1(ζ)表示绕x轴逆时针旋转ζ角度值,表示为: (15) 将其代入方程(10)整理得: (16) 来袭导弹在理论拦截点的速度矢量为VA=(vxa,vya,vza),则在拦截坐标系中的速度矢量为:VLA=LELVA。 同样也可以用此方法计算得出拦截弹飞行至在理论拦截点时,在拦截坐标系下的速度大小和方向。 来袭导弹和拦截弹交汇在拦截点,所以在拦截过程当中,在拦截弹上建立的拦截坐标系和在来袭导弹拦截点上面建立的拦截坐标系重合。当来袭导弹的弹道轨迹确定时,若要在理论拦截点进行拦截,拦截弹必须到达拦截点高度,当在理论拦截点的拦截弹的速度大小是确定时,通过改变拦截点发射点可以改变拦截弹在理论拦截点的速度方位角,从而求得不同交汇角下的拦截概率值。 在改变不同的交汇角度时,相当于将拦截弹在拦截点下的速度矢量绕拦截坐标系的y轴进行旋转。本文在进行拦截概率计算时,只考虑逆轨拦截情况,即在理论拦截点处来袭导弹的速度平面和拦截弹速度平面的夹角范围为[π/2,3π/2]。 本文将拦截弹的发射方位角A0,最大理论攻角α(亚声速段攻角绝对值的最大值),从发射到理论拦截点的飞行时间t,作为发射诸元。当给定A0,α,t,可以在拦截弹的空间杀伤区内唯一确定一点。同样在以拦截弹发射点为原点建立的坐标系中,给定Ac,lc,hc也可以唯一确定一点,AC为选择的目标点在以发射点为原点建立的坐标系中与x轴正向的夹角,lC为目标点在地面的投影在地球表面距离发射点的距离,hC为目标点的高度。拦截弹在空间区域的杀伤区即为由(A0,α,t)到(Ac,lc,hc)的一对一映射。利用插值的方法对其进行逆运算求解。 将拦截弹在图1中的空间杀伤区用一组同心球面进行划分,每个球面上再进一步剖分。选择同一个球面上与理论拦截点的方位角Ac,射程lc,高度hc彼此相邻的9个轨迹点,形成一个类似于正方形的小面元,选择与该球面相邻的两个球面,形成一共27个点的正方体,如图5所示 图5 球面上9点构成的微元 在计算求解的过程中选取适当的网格剖分精度,确保每个正方体微元有足够小的尺寸。选定一个理论拦截点c=(Ac,lc,hc),选择正方体微元中与理论拦截点距离最近的一个网格点q=(AREF,lREF,hREF)作为参照点,当微元足够小时,按二阶泰勒展开有下列方程: (17) 假设来袭导弹的弹道数据已知,依据拦截弹的最大拦截高度,由图1可知拦截弹的拦截高度范围在80~430 km,确定在来袭导弹的轨迹上面的在该高度范围内的弧段为可拦截弧段。拦截点可能发生在可拦截弧段的任意一点。其求解步骤为: 1)选定某一可拦截弧段上面的点作为理论拦截点,依据方程(10)和(11)求解出理论拦截点处的经纬度。并将来袭导弹在理论拦截点处的位置速度矢量投影在拦截坐标系。 2)依据建立的拦截弹在空间中的杀伤区内选定在理论拦截点高度上可达到的可达集轨迹,在这些可达集轨迹点中选择某一点作为理论拦截点,由此选出某一条符合条件的拦截弹轨迹。移动该拦截弹弹道轨迹,使其在理论拦截点处的点与来袭导弹的弹道轨迹上面的理论拦截点重合。 3)将拦截弹弹道轨迹绕拦截坐标系的y轴进行旋转从而改变拦截弹和来袭目标的交汇角。如图6所示。 图6 拦截弹和来袭导弹在拦截点交汇示意图 4)求解拦截弹发射点所在的经纬度和发射诸元参数。 在拦截弹的杀伤区内,假设选取理论拦截高度处一个点c=(Ac,lc,hc),利用插值法,将选取的27个点代入公式(17)求得该点的发射诸元参数。 此点与拦截坐标系原点重合,在步骤1中根据求得的理论拦截点的经纬度坐标,确定一个拦截弹道和来袭弹道在理论拦截点的平面夹角θC。假设在理论拦截点时刻,来袭导弹的速度在拦截坐标系内的xz平面内的投影与x轴方向的夹角为θA。则拦截弹道平面与x轴方向的夹角为: θI=θA+θC (18) 计算拦截弹发射点在拦截坐标系下的位置坐标。其位置关系如图7所示。 图7 发射点与拦截点球面三角形 图中OL为拦截点在地球表面的经纬度,OI为拦截弹发射点在地球表面的经纬度,lC为拦截弹发射点到拦截点在地面上的投影的距离。OI为拦截弹弹道平面与正北方向的夹角。θLI为发射点和拦截点的经度差。 利用球面三角形边的余弦公式 (19) 求得发射点的纬度BI。在利用球面三角形的正弦公式: (20) 求得发射点和拦截点的经度差,则发射点的纬度为: CI=CL+θLI (21) 通过求解的理论拦截点的发射诸元参数,可知拦截弹飞行至理论拦截点的时间为tI,来袭导弹飞行至理论拦截点的时刻为tL,则拦截弹的发射时刻为: t0=tL-tF (22) 在地心坐标系下建立来袭导弹相对于拦截弹的运动方程,拦截弹的位置矢量为: WI=(wIx,wIy,wIz),拦截弹速度为VI=(vIx,vIy,vIz),来袭导弹的位置矢量为:WA=(wAx,wAy,wAz),来袭导弹的速度为VA=(vAx,vAy,vAz)。则弹目相对距离为: (23) 相对速度为: (24) 相对距离: (25) 当弹目距离为L时,拦截弹捕获目标,并根据目标状态进行采用理想比例导引进行修正。 在拦截过程中,视线方向为拦截弹质心到来袭导弹的质心的矢量,则视线法向的相对速度为: (26) 拦截弹捕获目标的初始时刻,拦截弹和来袭导弹的位置和速度在拦截坐标系上的3个分量误差均服从高斯分布。利用公式(1)~(4)求解出在该交汇角度下的在理论拦截点处的拦截概率。 在拦截器捕获目标的初始时刻,拦截器和目标的位置速度由理论弹道值和误差值的和,在该时刻都是服从标准高斯分布的误差。假设位置差的任意方向的误差为r~N(0,1 000m),速度任意方向的误差为v~N(0,10m/s)。 在可拦截弧段上选取h=100 km,h=200 km,h=300 km,两个速度平面夹角从90°到270°时,拦截概率的变化值如图8所示。 图8 拦截概率随速度平面交汇角的变化 由图可知在拦截概率在速度平面夹角为从90°到180°再到270°时,拦截概率先降低后升高,在180°时拦截概率最低。碰撞交汇角对拦截概率的影响最大为0.15左右。 在杀伤区内的同一拦截高度处可以有很多个拦截点,这些拦截点可以由距离拦截弹的地表距离决定,拦截概率随着地表距离的变化如图9所示。 图9 拦截概率随据发射点地表距离的变化 由图可知拦截概率距离发射点越远拦截概率越高。由图8至图9可以看出拦截概率随着拦截高度的增加而减少。拦截高度作为单一变量对拦截概率影响如图10所示。 图10 拦截概率随着拦截高度的变化 针对反导武器在杀伤区内的拦截概率问题,在假定来袭弹道轨迹确定的情况下,通过在拦截弹杀伤区内选取在不同高度,不同地表弧段距离的拦截点,在不同交汇角下的拦截概率值,可以得出以下结论: 1)当交汇角为单一变量时,拦截概率随着交汇角的增加而降低。 2)当拦截高度为单一变量时,拦截概率随着高度的增加而增加,即在越高的地方拦截概率越好。 3)当拦截点距发射点的地表距离为单一变量时,拦截概率随着距离的增加而增加,即在距离发射点越远的地方拦截越好。 上述3个变量成为影响杀伤区内拦截概率的主要因素,根据本文建立的模型,当来袭弹道数据和上述3个变量都已知时,可以对拦截概率进行相应的计算。将拦截概率与理论拦截点在杀伤区内的位置关系对应起来,为反导作战和部署提供一定的参考。 另外本文中采用简化的末制导相对运动模型,拦截过程和实际有一定的差距,并且拦截成功与否还与多方面因素相关,若要得到高精度的拦截概率必须综合考虑各方面因素。 [1] 鲜 勇,郑晓龙. 弹道导弹攻防仿真系统建模[M]. 北京:国防工业出版社,2013.9. [2] 郭 宁, 姬聪生. 动能拦截弹弹目碰撞概率仿真建模技术[J]. 现代防御技术, 2011, 39(6):43-46. [3] 郭筱曦. “标准”-3导弹武器系统建模与攻防对抗仿真[D]. 哈尔滨:哈尔滨工业大学, 2011. [4] 陆伟宁. 弹道导弹攻防对抗技术[M]. 北京:中国宇航出版社, 2007. [5] 石 磊, 张雅声, 赵 晶. “标准-3”拦截弹对机动弹拦截有效性分析[J]. 现代防御技术, 2011, 39(2):29-34. [6] 王 磊, 蔡远文, 许 莉. 基于约束集分析的广义拦截区研究[J]. 装备学院学报, 2012, 23(2):59-62. [7] 刘世勇,吴瑞林,周伯昭. 大气层外拦截器末段轨控发动机开关控制律[J]. 宇航学报,2005(S1):106-109. [8] 崔维成,徐向东,邱 强.一种快速计算随机变量函数均值与标准差的新方法[J].船舶力学.1998,6(2):50-60. [9] 胡泽保,张振鹏. “标准-3”拦截弹导弹发动机参数复原设计[A].固体火箭推进技术学术会议[C],2004. [10] 温羡乔.美海军弹道导弹防御系统分析[J].863先进防御技术,2005(7). [11] 骆文辉, 杨建军. 动能拦截武器拦截仿真中的坐标系及坐标转换[J]. 弹箭与制导学报, 2007, 27(5):289-292.2 反导拦截模型分析
2.1 拦截过程分析

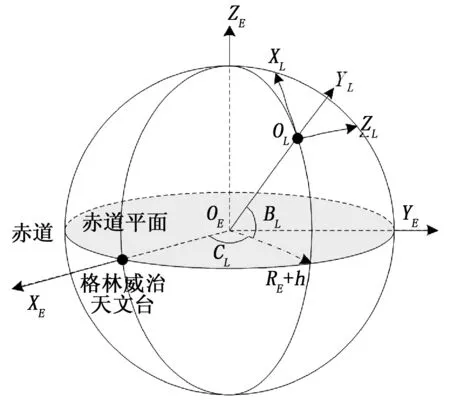
2.2 拦截弹发射诸元计算模型分析


3 拦截概率的求解步骤
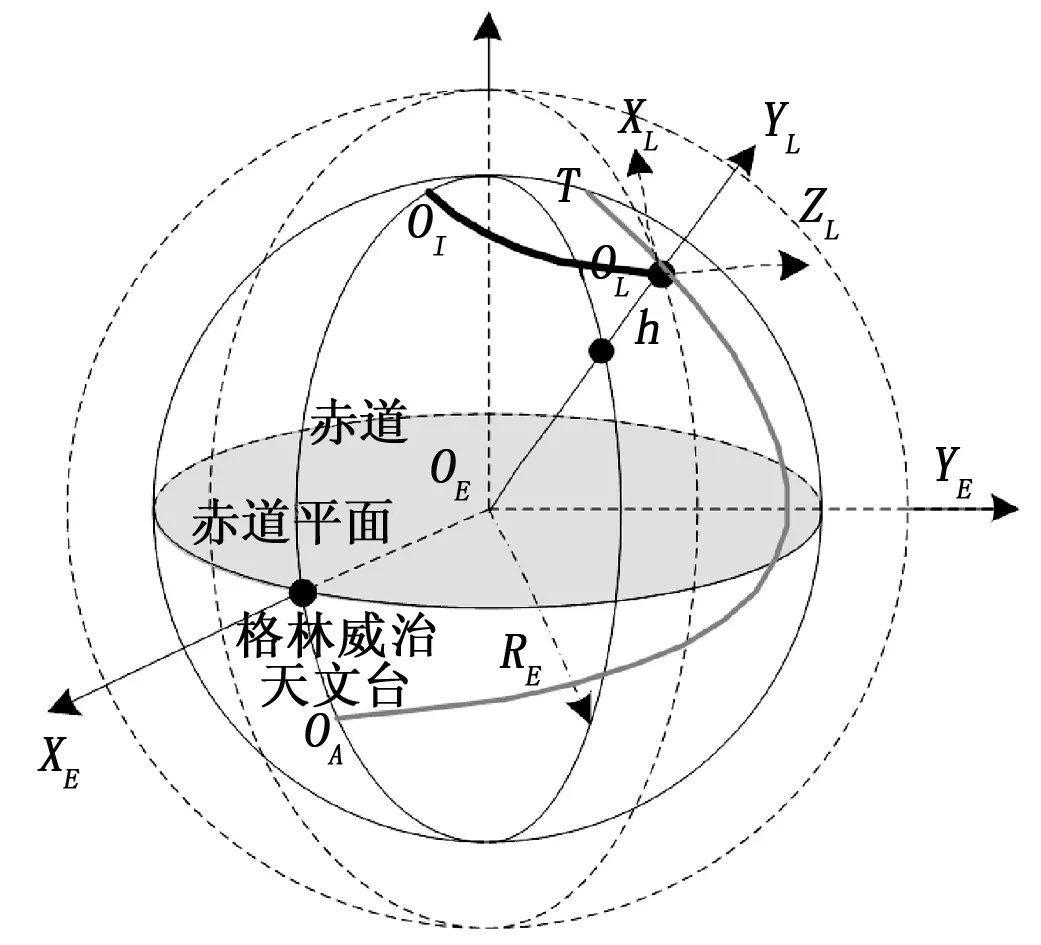

4 仿真结果及分析


5 结论
