基于新型组合积分控制器的积分过程先进控制

,,

(东华大学 信息科学与技术学院，上海 201620)

0 引言

实际工业生产过程控制中，常常会遇到具有积分特性的环节，例如化工过程中的大多数液槽、气罐、原料或成品存贮系统，它们的模型可以用积分加纯滞后环节描述。此类控制对象在阶跃输入的作用下，其输出不能自动地达到稳定状态，而是持续地增大或者减小；且由于具有延时环节的存在，输出不能及时地反映出过程的变化[1]。因此，这类对象控制的难度较大。自从Astrom[2]等发表文章以来，针对此种控制对象的研究就变得非常的活跃。一些文献对这类对象提出了各种各样的控制方法，但或多或少都存在一些问题：1)控制器的设计难度较大，不利于现场的实施；2)控制器的参数整定繁琐，且参数无明确的物理意义；3)对于干扰和模型失配较为敏感，无实际应用价值。针对上述问题，文献[3]根据内模控制的理论提出了一种二自由度PID调节器的设计方法，它仅具有两个参数，且系统的目标值跟踪特性和干扰抑制特性和参数之间具有单调变化的关系；文献[4]提出了一种积分过程PID自整定方法，引入反馈机制将积分过程转换为稳定过程，在此基础上基于鲁棒指标设置PID控制器，为积分加纯滞后对象的控制提供了一种新的方法。

本文提出了一种针对积分加纯滞后过程的新型双闭环组合积分控制算法。这种控制算法由内环和外环两个组合积分控制器叠加而成，内环用于将系统稳定，外环用于消除输入干扰的影响和改善控制系统的动态性能。这种控制器可调参数少，且参数具有明确的实际意义。

仿真结果表明，该控制器抑制干扰能力强，在模型失配时仍然能够保持良好的控制特性，鲁棒性能较好；同时对于时间常数较大的一阶加纯滞后系统也有着良好的控制作用。

1 组合积分系统及其先进控制算法

虽然组合积分系统已经广泛存在于例如钢铁、石油化工、谷物加工、烟草生产、打叶复烤、矿物处理等一系列工业过程之中，但是截止目前，在国内外的期刊杂志上，还没有发现有关组合积分系统的研究文献，国内外的著名过程控制大师也没有研究过该类对象，很多工程人员把这类过程简化为普通的一阶加纯滞后环节。下面列出5种典型组合积分对象的传递函数：

(1)

(2)

(3)

(4)

(5)

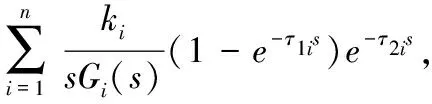
对于组合积分系统，即使是在无模型失配的情况之下，PID控制器的控制效果也很不理想，很难在响应速度和鲁棒稳定性之间取得平衡。同时，随着工业的高速度发展，对产品的质量、能源消耗和环境保护要求越来越高，对过程控制的精度要求也越来越高，传统的控制算法对组合积分对象的控制越来越不适应，迫切需要一种新的控制理论、方法和理念来指导组合积分控制系统的设计、整定和操作。因此，设计一种基于模型的控制算法是非常必要的。

假设过程对象的传递函数具有式(2)的形式，而所期望的闭环传递函数的结构形式为：

(6)

其中：τ10,τ20,λ是整定参数。当λ=1，开环响应时间与闭环响应时间相同；当λ>1，开环响应时间快于闭环响应时间；当λ<1，开环响应时间慢于闭环响应时间。

这样可以推导控制器的传递函数为：

(7)

假设λ=1,τ10=τ1,τ20=τ2,k0=k，则有：

(8)

控制器Gc的输入输出关系为：

(9)

式(9)的第一项为比例项，第二项可以解释为控制器在t时刻的输出是基于控制器在时间[t-(τ10+τ20),t-τ20]的输出预测得出的，故该控制算法在实际的工业应用中简单易行。

如果在控制器上加一个阶跃输入，首先由于比例项的存在，阶跃响应会出现初始的阶跃，而后在一段时间内保持不变，后来在变积分的作用下上升，最后在稳定的积分作用下而平稳上升。该控制器即具有PI控制器的特性，又具有预测的功能，故命名为伪预测PI控制器，又叫组合积分控制器。若τ20=0，得到的简化组合积分控制器为：

(10)

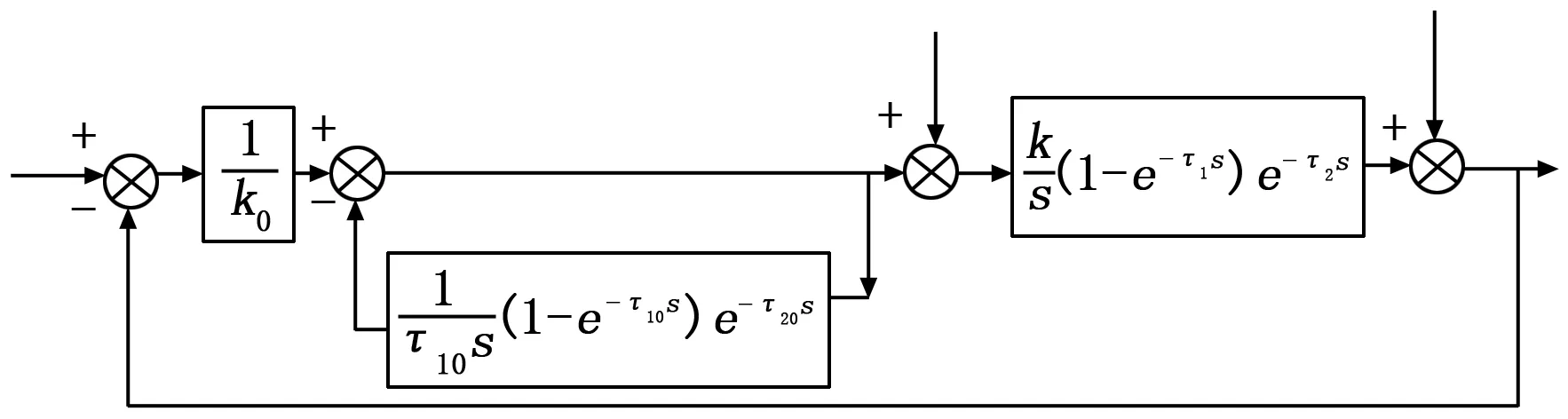
图1 组合积分控制系统结构

组合积分控制器是针对组合积分对象提出的，对组合积分对象有着良好的控制作用。将该控制器进行推广，可以运用到非组合积分对象上，且效果较为理想，例如典型的一阶加纯滞后过程、二阶加纯滞后过程以及一些高阶系统等。

2 双闭环组合积分控制系统结构

考虑具有如下传递函数的积分加纯滞后对象：

(11)

其中：K′，L′为不确定参数。

在正常情况下，该被控对象所对应的标称模型为：

(12)

基于(8)标称模型设计制器。假设所期望的闭环传递函数为：

(13)

其中：τ1为控制器的可调参数，其值越大则Gq1的闭环响应速度越慢，越小则闭环响应速度越快。根据闭环传递函数可以反推：

(14)

控制器Gc1(s)的输入输出关系为：

u1(s)=

(15)

u1(s)的第一部分是线性部分，第二部分的拉普拉斯变化为：

(16)

式(16)的结果可以理解为u(v)在时间[t-(L+τ1),t-L]上进行积分后，再取这段时间内的均值。这一形式本质上相当于算术平均值滤波的作用，即均值滤波器[6]。

这种控制算法有着较好的闭环响应性能和鲁棒稳定性，但是对积分时滞对象来说，探讨控制器的设计不仅仅是为了促进对积分时滞过程的研究，而且能够在实际应用中实现对扰动的有效抑制。如果仅仅使用上述单闭环组合积分控制算法，当干扰存在时，输出存在静态余差，缺乏实际应用价值。

针对这种情况，将上述整个组合积分系统视为一个对象，其传递函数同式(13)，对该对象设计组合积分控制器。假设所期望的闭环传递函数为：

(17)

控制器Gc2(s)为：

(18)

其输入输出关系为：

(19)

从式(15)可以看出，Gc2(s)为典型的组合积分控制器。将Gc1(s),Gc2(s)和控制对象G′(s)所构成的新型控制系统，称之为双闭环组合积分控制系统，Gc2(s)为主控制器，Gc1(s)为副控制器，结构如图2所示。

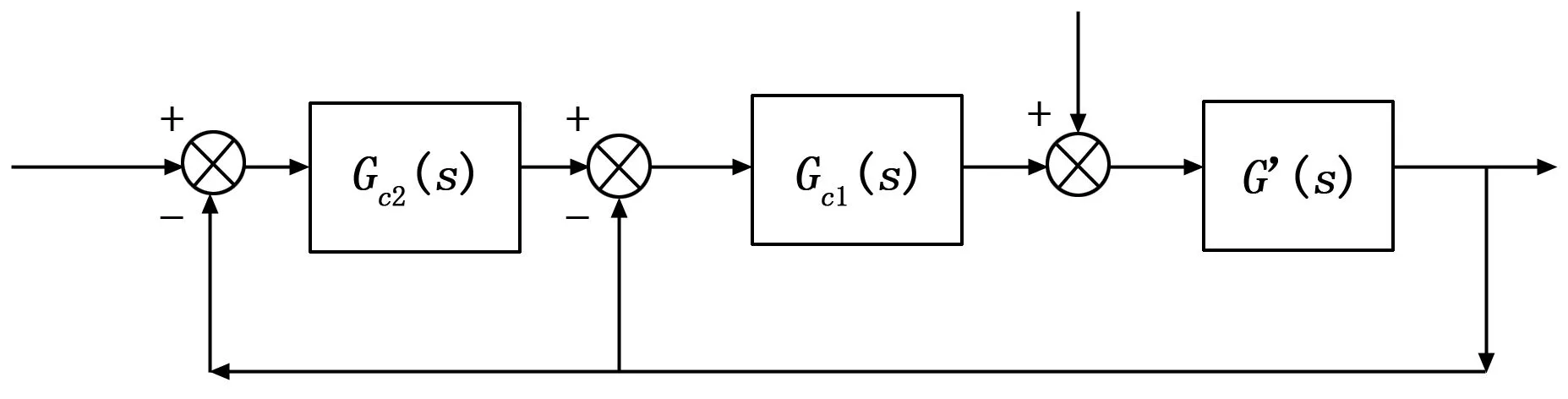
图2 积分过程对象双闭环组合积分控制系统的结构

系统对设定点的响应传递函数为：

(20)

令A(s)=τ2s-(1-e-τ2s)e-Ls，B(s)=τ1s-(1-e-τ1s)e-Ls，将式(11)，(14)，(18)带入式(20)中可以得到：

Hr(s)=

(21)

系统对干扰的响应函数为：

(22)

将式(10)，(14)，(17)带入式(22)中可以得到：

Hd(s)=

(23)

且，所以系统输出在稳定时不存在余差。

在无模型失配的时候，即K′=K,L′=L，系统对设定点和对干扰的响应函数为：

(24)

(25)

τ1越小，系统的抗干扰性越强，但鲁棒性会变差；τ1越大，系统的抗干扰性越弱，但鲁棒性较好。

3 仿真研究

选取燃油锅炉蒸汽压力控制系统，燃油调节阀的开度u(%)为被控对象的输入，蒸汽压力y(MPa)为对象的输出，在工作平衡点处求取对象的动态模型，得到如下的传递函数为[7-8]：

在正常情况之下，内环的闭环响应时间和外环的闭环响应时间相同时，该控制器的鲁棒性能较好。设定系统的目标值输入为r(t)=1(t)，在350s时加入一个幅值为-0.5的阶跃干扰，输入为d(t)=-0.5*1(t-350)。

分别选取τ1=τ2=10，τ1=τ2=20，τ1=τ2=30三组不同的参数，验证在不同参数条件下控制器的各项性能指标。

综合比较图3、图4，表明：当τ1、τ2越大，控制器的抗干扰性能越差，上升时间越慢，但鲁棒性能越好；τ1、τ2越小，控制器的抗干扰性能越好，上升时间越快，同时鲁棒性能越差。因此，控制器的抗干扰性能和鲁棒性能是成反比的。

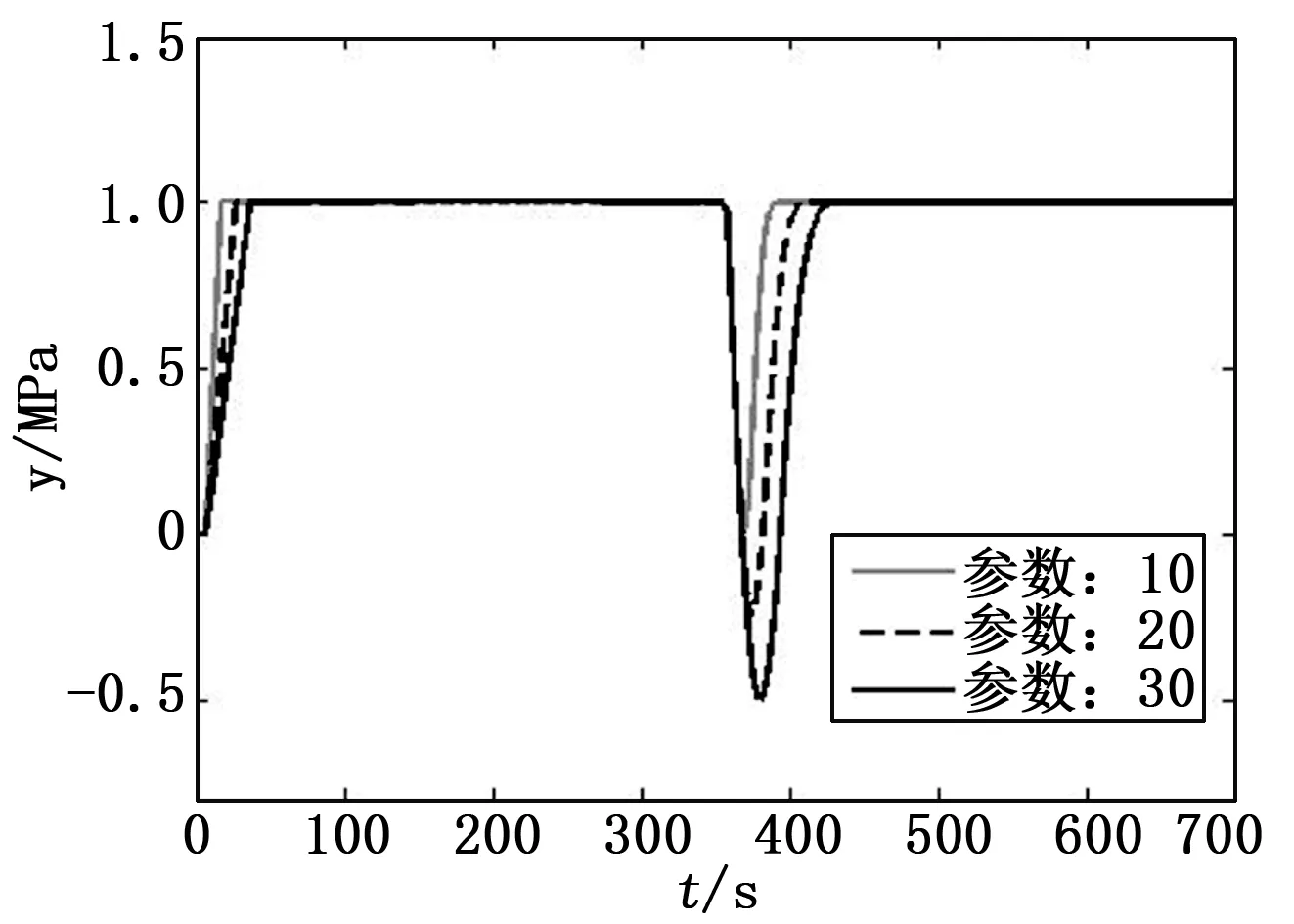
图3 标称模型、不同参数条件下的阶跃响应曲线

图4 模型失配10%、不同参数条件下的阶跃响应曲线

比较文献[3]、文献[4]以及本文提出的3种策略下系统的控制品质，其中文献[3]二自由度PID的参数选择为

λ

1

=5，

λ

2

=10，文献[4]的参数选择为

M

s

=1.6，双闭环组合控制器的参数

τ

1

和

τ

2

取值为15。在无模型失配时，得到如图5所示的仿真比较结果。

从图5中可以看到，在初始上升阶段，双闭环组合积分控制算法达到稳态设定值的时间是最短的，且相较于其他两种控制算法无超调；当存在干扰时，双闭环组合积分控制算法振荡峰值较小，且重新回到稳态的时间最短，抗干扰性能最优。同时，双闭环组合积分控制器的输出结果是以直线的形式上升，在某些特定的工业生产过程中有着更好的实用价值。

为了验证系统对模型失配的抑制能力，假设实际对象的时间和对象模型产生±10%的误差，得到的输出响应如图6所示。

可以看出，当模型失配且存在干扰信号时，系统的控制效果良好，超调量小，输出能很快地跟踪到给定值，故该控制算法对于模型失配具有较好的抑制性能，鲁棒性能较好。

综合考虑快速性、抗干扰性和鲁棒性能，可以认为双闭环组合积分控制器对于积分加纯滞后系统是一种较为有效的方法，跟踪设定值较快，抗干扰能力较强，鲁棒性能较好。同时由于参数的可调节性，在实际的工程项目中，可以根据实际需求来调节参数以获得最佳的控制效果。

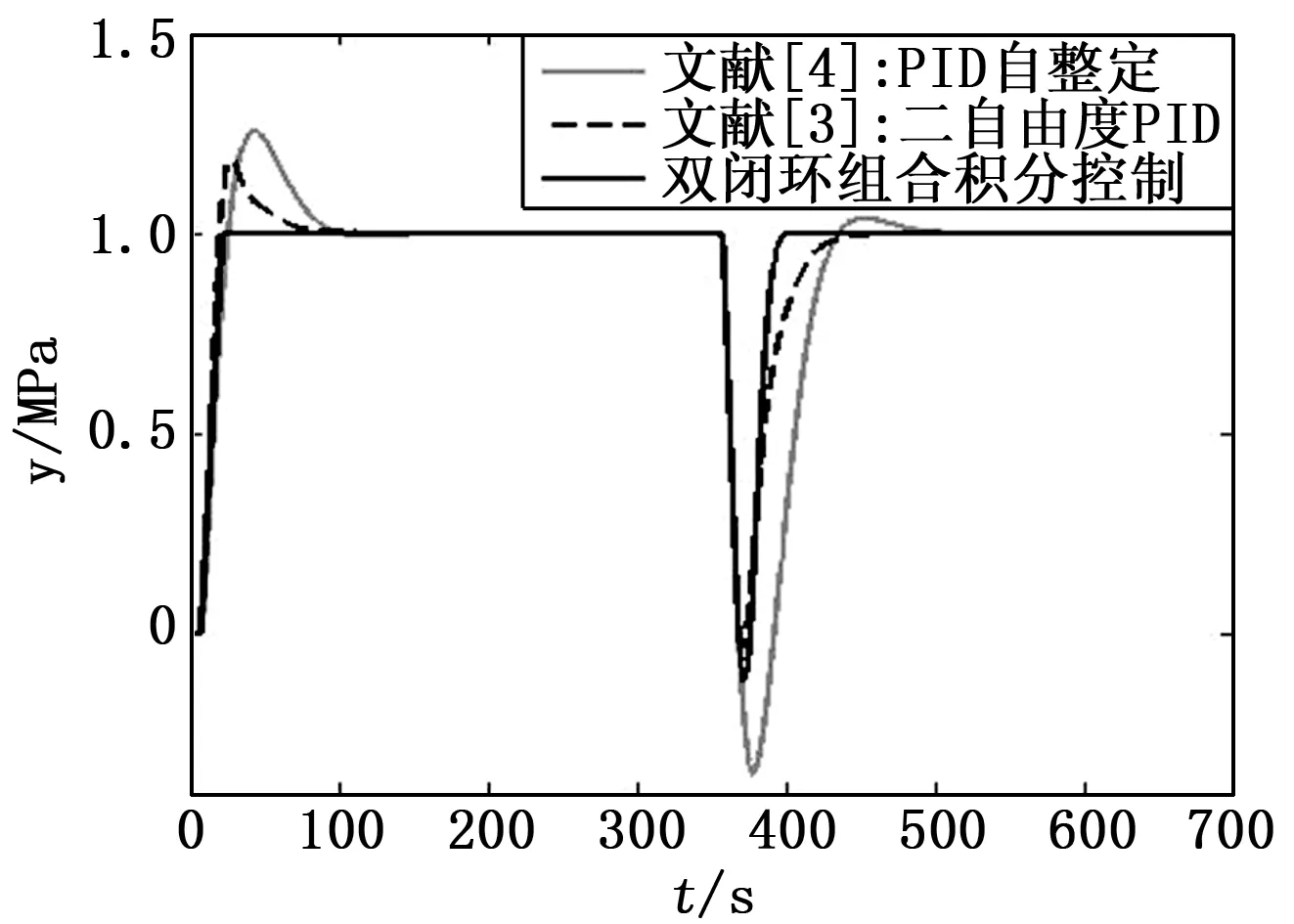
图5 标称模型下的阶跃响应曲线

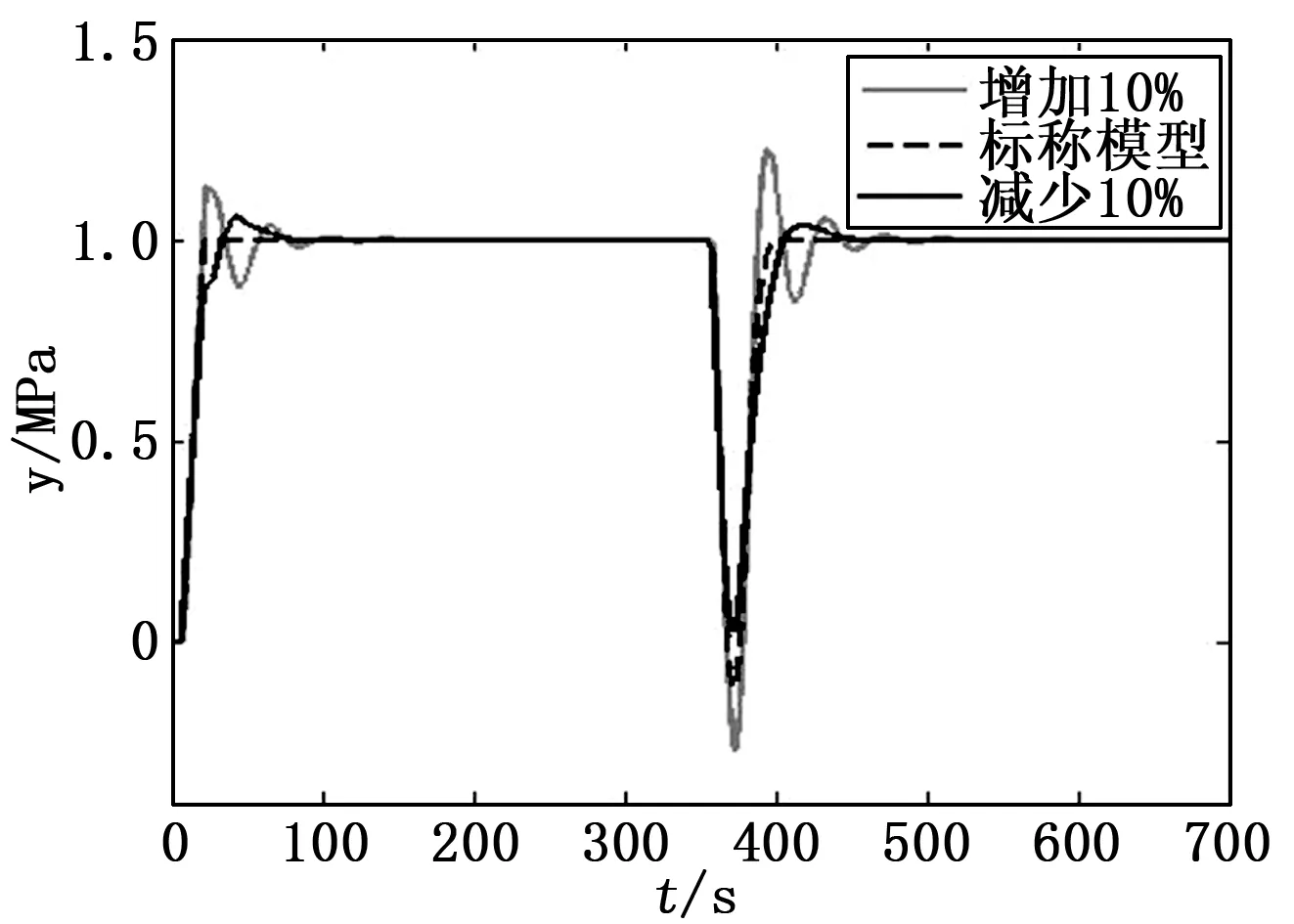
图6 标称模型、模型失配下的阶跃响应曲线比较图

在实际的工业生产环境中，对于时间常数较大的一阶加纯滞后环节，可以将该对象近似为积分加纯滞后环节。选取文献[9]中简化后的纺织温度控制系统模型：

将其简化为积分加纯滞后模型：

以G′(s)为对象设计双闭环组合积分控制器来控制实际G(s)，综合考虑后双闭环组合积分控制器的参数选择为τ1=τ2=120。在700 s时加一个幅值为-0.5的阶跃干扰，比较阶跃输入、标称模型和模型失配10%的系统输出，得到如图7所示的仿真结果。

从图7可以看出，对于时间常数较大的一阶加纯滞后系统：在标称模型下，双闭环组合积分控制器对干扰有着很好的抑制效果，输出无静态余差；在模型失配时输出无超调且能够较快的达到设定值，具有较好的鲁棒稳定性。

因此该控制算法对于时间常数较大的一阶加纯滞后系统亦有着良好的控制效果，能够有效抑制干扰，鲁棒性能较好。

图7 标称模型、模型失配时的跃响应曲线

4 结论

本文针对工业过程控制领域中常见的积分加纯滞后对象，提出了一类双闭环组合积分控制算法，并给出了它的结构形式。这种控制算法结构简单，可调参数少，具有明确的物理意义，且整定过程相对简单。理论分析了该控制算法在设定值跟踪和扰动消除方面的有效性。仿真结果表明，该控制算法具有较好的目标值跟踪特性和抗干扰性，且鲁棒性较好，同时对于时间常数较大的一阶加纯滞后系统也有着非常良好的控制效果。

[1]温 馨，石红瑞.积分过程的二自由度PID控制及应用[J].控制工程，2013，20(S0)：206-209.

[2]Astrom K J,Hanf C C,Lim B C.A new Smith predictor for controlling a process with an integrator and long dead-time[J].IEEE Trans on Automatic control,1994,39(2)：343-345.

[3]张井岗,刘志远，裴 润.一类非自衡对象的二自由度PID控制[J].控制与决策，2002，17(6)：886-889.

[4]赵永郭，贾 磊，蔡文剑.一种积分过程PID自整定方法[J].山东大学学报(工学版),2002,38(1)：48-52.

[5]任正云，郑 达.流程工业的组合积分系统及其先进控制[J].控制理论与应用，2009，26(9)：1009-1013.

[6] 郑 达,方建安. 组合积分系统的控制理论与应用研究[D]. 上海:东华大学,2009.

[7]Chien I L,Sheng C P,Liu J H.Simple control method for integrating processes with long deadtime[J].Journal of Process Control,2002,12(3)：391-404.

[8]Astrom，K.J.A new Smith predictor for controlling a process with an integrator and long deadtime[J].IEEE Trans on Automatic Control,1994,39(2)：343-345.

[9]谢水英.基于一阶加纯滞后模型的纺织生产过程温控PI系统设计[J].世界科技研究与发展.2015，37(5)：556-559.