北斗定位系统在轨道参数测量上的应用
2018-02-05余明
,,余明
(中南大学 信息科学与工程学院,长沙 410075)
0 引言
随着技术的不断提升,我国高速铁路正以难以置信的速度飞速发展。轨道的老化、地面沉降以及铁路维护不当会导致线路平顺性下降,会对列车造成多种负面影响,降低其运行的安全性和平稳性。尤其是对于现在的高速列车,轨道平顺性下降会大大增加列车脱轨风险[1-3],对人民生命财产安全造成巨大威胁。
轨道的平顺性评估指标主要包括轨距、轨向、高低等参数,统称为轨道外部几何参数。其中,轨向参数,由于其自身特点,传统检测仪器因积分误差影响较大,无法精确检测。亟待一种新型测量手段对该参数实施准确有效的检测。
国内外专家学者对轨道外部几何参数检测问题都进行了深入研究并设计生产了一系列测量设备。国外比较典型的轨道综合检测车有East-i和阿基米德等,另外德国的GEDO CE轨检仪和瑞士的GRP系列轨检仪在铁路检测中应用较为广泛。国内应用较广的轨检车主要是GJ-3、GJ-4、GJ-5等[4],另外日月明公司的GJY-H-5轨检仪、瑞邦研发的SGJ-T-RB-1型客运专线几何状态测量仪等[5-6]也是极具代表性的轨检设备。但是传统轨道测量设备普遍存在价格高昂、效率低下、积分误差等缺陷。
利用日趋完善的北斗定位系统设计了一种新型轨道外部几何参数测量系统。该系统由北斗定位系统、配备北斗卫星接收机的轨检仪及数据处理终端等三部分构成。建立基于移动基站的动态短基线观测控制网,对数据进行站间和星间双差处理。基于多频观测量的线性组合,得到超宽巷、宽巷、中巷及窄巷观测量,采用逐级模糊度确定法固定整周模糊度,即沿着从超宽巷到窄巷的顺序依次求解整周模糊度。解算出天线相位中心的准确坐标并作平差处理,利用线性拟合方法拟合所需测量点并计算当前弦长下轨道轨向值。
1 系统工作原理
1.1 测量系统结构
测量系统主要由北斗定位系统、配备北斗卫星接收机的轨检仪和数据处理终端构成。整体方案结构如图1所示。

图1 系统结构图
基于北斗卫星高精度定位的新型轨检设备利用动态基站对数据进行双差处理,并采用几何无关算法固定整周模糊度,实时获得接收机天线的中心位置坐标,平差后对测量点进行线性拟合并计算轨向,其余参数由轨检仪上专用传感器测量,具体测量流程如图2所示。
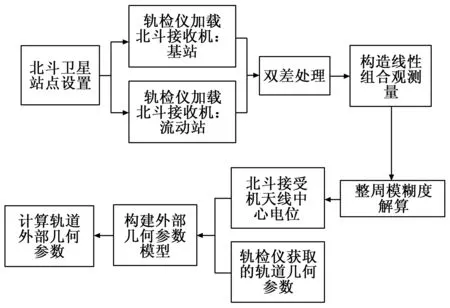
图2 检测流程图
1.2 动态短基线构造
北斗动态短基线是由两台加载在轨检仪上的北斗卫星接收机组成,在一段时间内进行连续观测采样。针对铁路线路狭长且周围环境复杂不易建立固定基准站的特点,在基准站和流动站同时移动的情况下实现相对定位。北斗卫星接收机及天线安装方式如图3所示。

图3 接收机与天线安装示意图
基线长度标定为1米,对接收机载波相位观测数据进行双差处理,在短基线条件下,可最大程度上消除对流层延迟、电离层延迟等公共误差和时钟误差。
1.3 观测数据处理
载波相位是北斗卫星接受机从卫星信号中获取的一个基本测量值,其观测方程式为:
φ=λ-1(r+c(δtu-δts)-I+T)+N+εφ
(1)
式中,φ为载波相位测量值;λ为载波波长;r为接收机到卫星的几何距离;c为真空中的光速;δtu为接收机钟差;δts为卫星钟差;I为以距离为单位的电离层延迟;T为以距离为单位的对流层延迟;N为整周模糊度;εφ为载波相位测量噪声量,包括多路径误差和接收机噪声等。
对载波相位观测量进行双差处理首先令流动站u和移动基站r分别对卫星i和j作单差处理,得到其单差测量值:
(2)
(3)
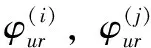
(4)

北斗导航系统可在3个频率载波上同时发射信号,频率分别为1561.098 MHz、1207.140 MHz和1268.520 MHz。三频双差载波相位测量值可分别表示为:
(5)
(6)
(7)
其线性组合为:
φk1,k2,k3=k1φ1+k2φ2+k3φ3
(8)
εφ,k1,k2,k3
(9)
式中,Nk1,k2,k3=k1N1+k2N2+k3N3;εφ,k1,k2,k3=k1εφ,1+k2εφ,2+k3εφ,3;
通过对不同频率信号上的双差观测量进行线性组合从而得到波长不同的组合观测量,将B1和B3的(1,0,1)组合称为窄巷组合,将B1与B2的(1,-1,0)组合称为中巷组合,将B1与B3的(1,0,-1)组合称为宽巷组合,将B2和B3的(0,-1,1)组合称为超宽巷组合。
1.4 几何无关算法固定模糊度
几何无关算法具有几何有关算法不具备的优点:1)不易受到测量值中对流层延迟误差的影响;2)求解针对某一刻卫星的测量值,几何有关算法通常需要五颗及以上卫星测量值;3)与用户接收机运动无关,无需推测其坐标值;4)方程解算一般自由度相对更高,模糊度求解值的正确性较易验证。因此RTK算法非常倾向于采用几何无关算法。
逐级模糊度确定法可视为LAMBDA算法的一种特殊情形,其算法的思路是基于宽巷测量值的整周模糊度比窄巷测量值的整周模糊度更容易求解这一事实,通过对多频测量值进行线性组合从而生成不同波长的组合测量值,并从宽到窄逐级求解各级模糊度。
1.4.1 利用双差伪距测量值求解双差超宽巷载波相位测量值φw32的整周模糊度
由超宽巷组合(0,-1,1)可得到双差超宽巷载波相位测量值φw32的观测方程式:
(10)
则超宽巷载波相位测量值的整周模糊度Nw32的值等于:
(11)

r+εφ,w32
(12)

由中巷组合(1,-1,0)可得到双差中巷载波相位测量值φw12的观测方程式:
(13)
则中巷载波相位测量值的整周模糊度Nw32的值为:
(14)

r+εφ,w12
(15)

由窄巷组合(1,0,1)可得到双差窄巷载波相位测量值的观测方程式:
(16)
则窄巷载波相位测量值的整周模糊度Nn的值为:
(17)

1.5 轨道外部几何参数测量模型
轨检仪上的两台北斗卫星接收机及天线分别安装在双轮梁两端,两天线相位中心距离标定为1米并采用上述算法得到精确的天线相位中心坐标。
1.5.1 测量点位置平差
计算轨向用的测量点取动态基线的中点。该定位算法采用基于移动基准站的差分相对定位,可分别令两台接收机为移动基准站获得该短基线向量,并根据其误差计算权重值进行平差,提高测量点位置精度。测量原理如图4所示。

图4 轨道纵面图
以N1为基准站,N2为流动站,解算得到基线向量V1,且可得到基线向量误差绝对值
(18)
同理,以N2为基准站,N1为流动站,解算得到基线向量V2,且可得到基线向量误差绝对值
(19)
根据ε1和ε2计算基线向量V1和V2权重值,有:
(20)
(21)
则M点坐标为:
(22)
1.5.2 轨向参数计算
得到M点精确坐标后,计算任意弦长轨向。由于北斗卫星接收机采样频率为1 Hz,任意弦长中点并非一定有采样点,因此采用线性拟合方法确定该点,拟合原理如图5所示。
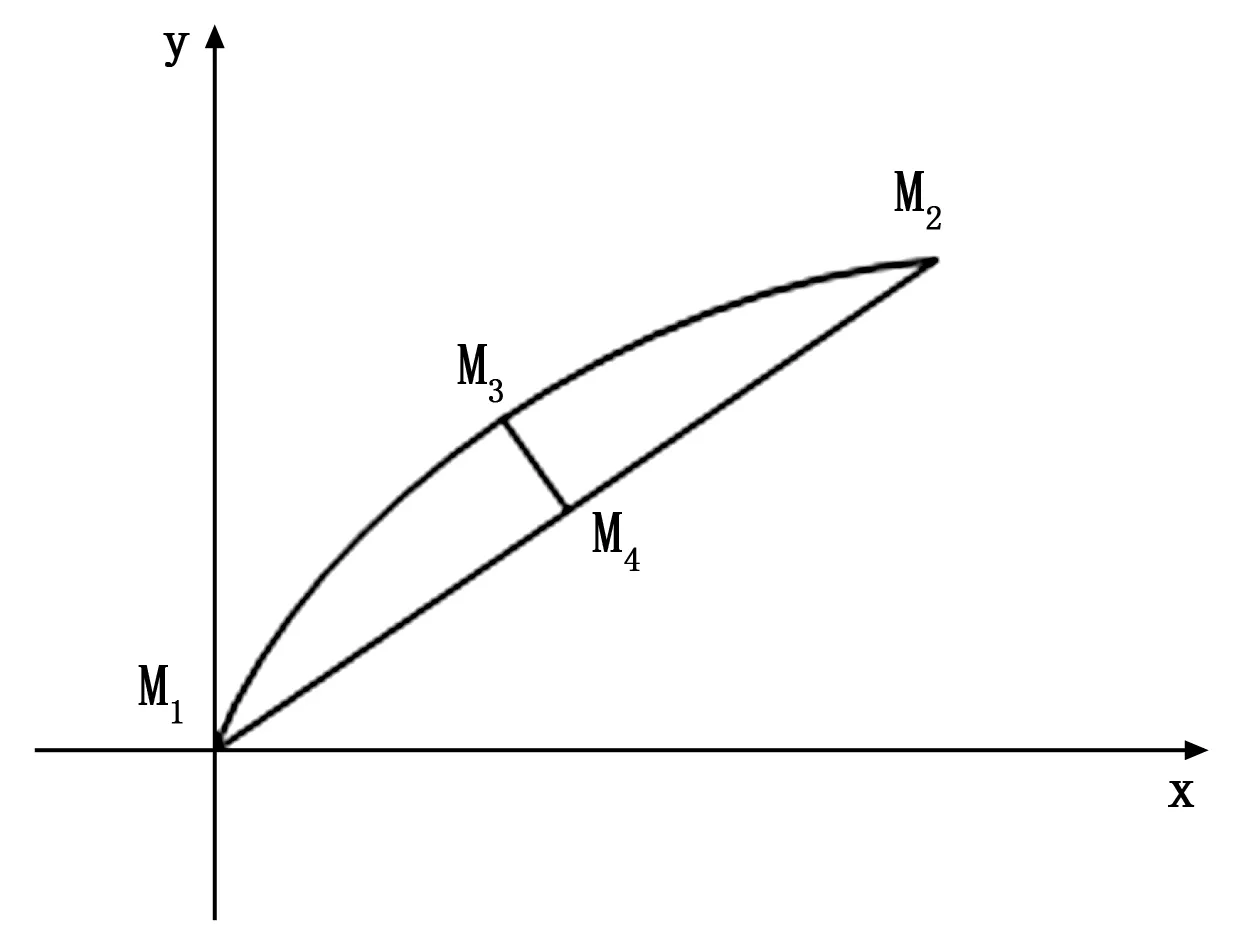
图5 拟合原理图
2 实验数据分析
2.1 静态实验
静态实验中使基准站和流动站分别固定于轨检仪双轮梁两端,并保持静止状态,对标定采样点进行静态采样。所用数据于2017年6月15日至6月19日每天上午9时至12时在中南大学铁道学院铁信研究所轨道实验室采集所得,采用两个司南导航四系统十一频接收机,型号均为M300NETGNSS(K708),两个型号为HX-CS7603A三系统七频天线(AT330)固定在基线长度为1 m的双轮梁两端。采样频率为1 Hz,日均采样时长为2小时45分,3个采样点日均获得18500个可用历元。按上文提出的算法对实测数据进行处理,轨向平差处理结果列于表1。在静态测量条件下,该系统静态测量计算所得轨向值平面误差小于0.6 mm,高程误差小于1.0 mm,达到静态观测精度要求。

表1 静态轨向误差
注:下标N表示北向,E表示东向,U表示天向
2.2 动态实验
为进一步验证该测量系统在短基线动态情况下的实用性,2017年6月21日至6月25日每天上午9时至下午5时于中南大学铁道学院铁信研究所轨道实验室进行动态实验,采样频率设为1 Hz,日均采样时间3小时,日均获得21 000个可用历元。
2.2.1 验证方案
按静态实验的方式安装好接收机和天线,启动接收机后静态观测半小时,随后按常规检测速度沿轨道步行向前推进,对基准站和流动站的原始观测数据和星历数据进行采集,利用上文提出的差分定位算法对实测数据进行实时处理并计算轨向值。
2.2.2 实验结果分析
按上文提出的算法对实测数据分析计算,轨向平差处理结果列于表2。在动态测量条件下,该系统动态测量计算所得轨向值平面误差小于13 mm,高程误差小于18 mm,基本满足本研究方案的测量要求。

表2 动态轨向误差
注:下标N表示北向,E表示东向,U表示天向
3 结论
1)针对铁路线路狭长且周围环境复杂不易建立固定基准站的特点,研究并设计了基于移动基准站的相对定位方法,极大地消除了公共误差,提高了测量精度。
2)采用北斗卫星接收机实时获取天线相位中心的观测数据,并与移动基准站进行双差处理,对不同频率观测量进行线性组合并用几何无关算法固定模糊度,提高RTK算法精度和效率。
3)将两台北斗卫星接收机分别设为基准站各计算一次基线向量,并按其基线向量误差大小计算权重值,对动基线中点的测量点做平差处理,进一步提高系统测量精度,得到轨向值测量的静态误差和动态误差分别为0.6 mm和13 mm。
4)基于北斗定位系统的全天候、全局性等特点,任意弦长不平顺问题都得以有效解决,使得轨道外部几何参数的测量不再收到陀螺仪等传感器由于精度引发的距离限制。
[1] 陈 强, 刘丽瑶, 杨莹辉,等. 高速铁路轨道几何状态的车载摄影快速检测方法与试验[J]. 铁道学报, 2014, 36(3): 80-86.
[2] 罗 林. 高速铁路轨道必须具有高平顺性[J]. 中国铁路, 2000, 10(9): 8-11.
[3] 伏思华, 于起峰, 王明志,等. 基于摄像测量原理的轨道几何参数测量系统[J]. 光明学报, 2010, 30(11): 3203-3208.
[4] 高春雷, 王发灯. 利用激光准直技术检测线路的长波不平顺[J]. 铁道建筑, 2009, 15(1): 81-85.
[5] Iyengar R N, Jaisal O R. Random field modeling of railway track irregularities[J]. Journal of Transportation Engineering, 1995, 121(4): 303-308.
[6] 胡庆丰, 安博格. GPR1000轨检小车进行无砟轨道检测的作业方法[J]. 铁道勘察, 2008(3): 17-20.
[7] He Lina, Ge Maorong, Wang Jiexian, et al. Experimental Study on the precise Orbit Determination of the BeiDou Navigation Satellite System[J]. Sensors, 2013, 13: 2911-2928.
[8] Li Min, Qu Lizhong, Zhao Qile, et al. Precise Point with the BeiDou Navigation Satellite System[J]. Sensors, 2014,14:927-943.
[9] Yang Yuanxi. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system [J]. Science China: Earth Science, 2014, 57(1): 144-152.
[10] Tang Weiming, Deng Chenlong. Triple-frequency carrier ambiguity resolution for BeiDou navigation satellite system[J]. GPS Solution, 2014, 18:335-344.
[11] 施 闯. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学: 地球科学, 2012, 42(6): 854-861.
[12] 李金龙. 北斗/GPS多频实时精密定位理论与算法[J]. 测绘学报, 2015, 44(11): 1297.
[13] Li Jinlong, Yang Yuanxi, Xu Junyi, et al. GNSS multi-carrier fast partial ambiguity resolution strategy tested with real BDS/GPS dual- and triple-frequency observations[J]. GPS Solution, 2015, 19: 5-13.
[14] Alippi C, Casagrande E, Scotti F, et al. Composite real- time image processing for railways track profile measurement [J]. IEEE Transactions on Instrumentation and Measurement, 2000, 49(3): 559- 564.
[15] 刘立龙. 动态对动态GPS高精度定位理论及其应用研究[D]. 武汉: 武汉大学, 2005.
