高Nb-TiAl合金高温力学行为本构建模仿真技术

董成利， 于慧臣， 焦泽辉， 孔凡涛， 陈玉勇

(1.中国航发北京航空材料研究院 先进高温结构材料重点实验室，北京 100095； 2.航空材料检测与评价北京市重点实验室，北京 100095； 3.材料检测与评价航空科技重点实验室，北京 100095； 4.哈尔滨工业大学 材料科学与工程学院，哈尔滨 150001)

TiAl合金具有低密度、高比强度、优异的高温性能等综合优点，因此广泛应用于现代先进航空发动机涡轮叶片的制造，成为代替传统镍基高温合金制造涡轮叶片的唯一候选材料，应用前景广阔[1-4]。据权威统计，超过40000件TiAl合金用于制造波音787飞机的GEnx 1B发动机低压涡轮叶片和波音747-8飞机的GEnx 2B低压涡轮叶片[5]。为了研发能够承受更高温度的TiAl合金材料，国内外相关科研人员在传统TiAl合金材料成分的基础上添加了一定量的Nb元素，从而研制了具有更高高温强度、更好抗氧化性的高Nb-TiAl合金，高Nb-TiAl合金的成功研制吸引了国内外业内科研人员的广泛、持续关注。针对不同成分和组织的高Nb-TiAl合金材料，国内外相关科研人员开展了不同试验条件下的力学性能测试与表征工作，高Nb-TiAl合金材料的性能测试与表征工作主要体现在室温和高温条件下的成分-组织-性能方面，力学性能主要涉及高Nb-TiAl合金材料的拉伸[6-8]、低周疲劳[9-11]、蠕变/持久[12-13]、裂纹扩展[14]和断裂特性[15-16]等。

尽管目前国内外相关科研人员针对高Nb-TiAl合金材料开展了许多的力学性能测试，但缺乏对高Nb-TiAl合金材料疲劳-蠕变交互力学性能的认知和了解。一方面，涡轮叶片在航空发动机服役工况下不可避免地要承受疲劳-蠕变交互载荷，高Nb-TiAl合金要取代镍基高温合金，就必须研究其疲劳-蠕变交互力学行为。另一方面，从涡轮叶片结构强度设计层面上讲，若要实现高Nb-TiAl合金的工程化应用，必须建立表征其综合力学行为的本构模型，从而实现涡轮叶片在服役工况下力学行为的数值仿真模拟和分析。宏观唯象Chaboche黏塑性统一本构模型常被用于镍基高温合金力学行为的有限元数值计算和分析，众多计算案例表明，宏观唯象Chaboche黏塑性统一本构模型能够准确表征和预测镍基高温合金的力学行为，计算精度较高。实际上，Chaboche黏塑性统一本构模型本质上是层次结构，可以进行合理的裁剪，即可以任意减少或增加相关内变量及其演化方程来实现对材料或结构从简单到复杂力学行为的数值模拟。

本研究针对高Nb-TiAl合金开展750 ℃条件下不同应变速率的单轴拉伸、低周疲劳、疲劳-蠕变交互和蠕变试验，建立考虑Ohno-Wang修正并耦合Kachanov损伤的Chaboche黏塑性统一本构模型，采用自适应的显式Euler法将微分形式的本构模型离散为差分方程组，并植入到有限元软件ABAQUS的用户材料子程序UMAT 中，对高Nb-TiAl合金的不同应变速率的单轴拉伸、低周疲劳、疲劳-蠕变交互和蠕变行为进行了有限元数值仿真模拟。

1 试验材料与方法

试验验材料为高Nb-TiAl合金，合金名义成分为Ti-45Al-8Nb-0.2W-0.2B-0.02Y (原子分数/%)，该合金具有均匀的近片层组织，且包含较细小的片层团(平均尺寸为50 μm左右)、分布于片层团周围的γ相、硼化物以及YAl2等。该高Nb-TiAl合金较之传统的近片层高Nb-TiAl合金拥有更多分布于片层团周围的γ相。另外，铸造过程造成了合金片层团的扭曲变形，具体原始显微组织见图1。

图1 高Nb-TiAl合金原始显微组织Fig.1 Microstructure of high-Nb TiAl alloy

为了获得高Nb-TiAl合金的高温综合力学性能，并校验后续本构模型对其综合力学行为的表征预测能力，针对高Nb-TiAl合金开展了750 ℃条件下的不同应变速率的单轴拉伸、低周疲劳、疲劳-蠕变交互以及蠕变试验。高Nb-TiAl合金的单轴拉伸、低周疲劳、蠕变-疲劳交互以及蠕变试样实物如图2所示。单轴拉伸试验在Instron-5982试验机上进行，试验方法参照GB/T 4338—2006 《金属材料 高温拉伸试验方法》执行，应变速率选择1×10-3s-1和5×10-3s-1两种形式；低周疲劳及疲劳-蠕变交互试验在MTS-810试验机上进行，试验方法参照ASTM E606/E606M—2012《应变控制的疲劳试验方法》执行，低周疲劳采用应变控制，加载速率为1×10-3s-1，疲劳-蠕变交互采用应变控制，加载速率为1×10-3s-1，保载形式分别为上保载60 s、上下各保载30 s和下保载60s三种类型，载荷波形见图3，其中tT表示上保载时间，tC表示下保载时间；蠕变试验在机械杠杆式高温蠕变持久试验机RJ—30试验机上进行，试验方法参照HB 5151—1996《金属高温拉伸蠕变试验方法》执行。

2 Chaboche黏塑性统一本构理论

2.1 弹性本构关系

一般地，金属材料的弹性变形部分服从广义虎克定律(Generalized Hook’s Law)。令{ε}=[ε11,ε22,ε33,γ12,γ23,γ31]和{σ}=[σ11,σ22,σ33,τ12,τ23,τ31]分别为应变向量和应力向量，则金属材料的弹性本构关系可以表示为：

{ε}=[C]{σ}

(1)

式中：[C]为柔度矩阵。

2.2 屈服函数

Chaboche黏塑性本构理论是与屈服准则相关联的。它总是假设存在某种理想的屈服状态，屈服函数F作为一个标量出现在本构方程中。当应力水平低于屈服应力时，非弹性变形并不出现，即F≤0，此时应力应变关系服从广义虎克定量。只有当应力状态达到足以引起屈服时才会有非弹性变形产生，此时F>0。另外，屈服函数F是与应力、温度和内变量相关的函数，其一般表达式如下[17]：

图2 高Nb-TiAl合金试样实物图 (a)单轴拉伸试样；(b)蠕变试样；(c)低周疲劳及疲劳-蠕变交互试样Fig.2 Solid specimens of high-Nb TiAl alloy (a)uniaxial tensile specimen； (b)creep specimen；(c)low cycle fatigue and creep-fatigue specimens

图3 高Nb-TiAl合金疲劳及疲劳-蠕变加载波形示意图 (a)低周疲劳；(b)上保载60 s； (c)下保载60 s；(d)上下各保载30 sFig.3 Loading waveforms of LCF and creep-fatigue interaction (a)LCF;(b) tensile dwell time 60 s; (c)compressive dwell time 60 s;(d)balanced dwell time 30 s

(2)

式中：T是温度；Vk(k=1,2,…,N)是N个内变量；σy是与加载速率相关的初始屈服应力；R是一个表示各向同性硬化的标量，表示由于各向同性硬化引起的应力(drag stress)；Xij称为背应力(back stress)，表示在黏塑性流动过程中，应力空间内屈服面中心(或等势面)的移动，描述了与方向有关的硬化。

有效应力偏量的第二不变量为

(3)

2.3 流动法则

在Chaboche黏塑性本构理论中，流动法则是与Von Mises屈服函数相关联的，即：

(4)

式中：Λ=Λ(F)是一个非负的标量函数。

将屈服函数表达式代入式(4)，经整理可得：

(5)

流动法则给出了非弹性应变率和应力、内变量之间所具有的与温度相关的函数关系。在Chaboche黏塑性本构理论中，将式(4)中的Λ表达为屈服函数F的一个幂函数：

(6)

式中：K和n都是与温度有关的材料参数；=uH(u)；H(u)是Heaviside函数(u≤0，H(u)=0;u>0，H(u)=1)。关于Φ(F)的其他具体表达形式在Perzyna的文章[18-19]中也有所论述，这里不再赘述。

从式(4)～(6)可以看出，在Chaboche黏塑性本构理论中，黏塑性势函数可以定义为以下形式：

(7)

黏塑性(非弹性)应变率是黏塑性势关于应力的偏导数：

(8)

2.4 各向同性硬化/软化模型

材料的各向同性硬化/软化需要硬化变量R来描述，即通过改变当前弹性域尺寸大小来实现。各向同性硬化/软化对应于塑性流动过程中应力的缓慢变化，表示屈服面在各个方向以相同的量在扩大或缩小。即通常发生在以下两种情况中：一是在单调塑性流动过程中，屈服面以较低的速率在各个方向以相同的量在扩大或缩小；二是材料经过大量循环而接近达到循环硬化/软化的稳定状态[17]。

一般来说，各向同性变量服从下面的演化方程：

(9)

式中：Q,b,γ和m都是材料参数；Qr是各向同性变量R的渐近值；Q+k是屈服面尺寸的渐近值。注意，Q具有应力的量纲，其他几个是无量纲的常数。

2.5 随动硬化模型

材料在循环变形过程中体现出的平均应力松弛和棘轮行为主要是一种各向异性硬化行为的体现，为了更好地描述平均应力松弛和棘轮行为，已有研究主要集中在随动硬化模型的发展方面。

Chaboche等采用非弹性应变率及其累积作为度量来描述非线性的随动硬化，具体形式如下：

(10)

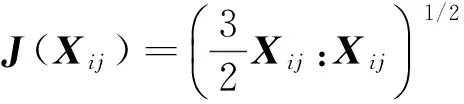
式(10)右边第一项表达了Prager线性运动硬化准则，但是仅限于单调加载；第二项为动态恢复，它使得硬化可以考虑到载荷方向的改变，如Bauschinger效应，该项的引入改善了硬化法则描述迟滞环的能力。第三项是后来单独加入的，描述了时间硬化恢复效应。

为了扩大模型的适用范围，可以将随动硬化变量分为几个分量，每个分量都遵从相同的非线性演化规律，具体形式如下：

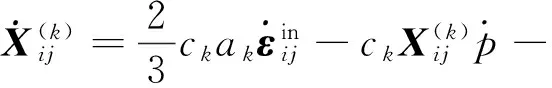
(11)

这样，总的随动硬化变量为：

(12)

2.6 蠕变损伤演化方程

蠕变损伤演化律采用Kachanov损伤方程[20-21]表达如下：

(13)

其中，pa，pr和pk是与温度有关的材料蠕变损伤参数。

对于各向同性材料，其损伤有效应力张量为:

(14)

为了考虑损伤的作用，须在以上所述的本构方程组采用损伤有效张量形式。Chaboche黏塑性统一本构模型的应用价值不仅体现在能准确模拟材料的复杂变形，而且也体现在可很好地与现有大型通用有限元程序相结合，为实际复杂结构和部件的强度分析提供良好的工具。由于ABAQUS有限元软件在非线性分析领域所具有的独特优势，特别是具有很强的数值稳定性和环境友好界面，因此本工作将Chaboche黏塑性统一模型通过ABAQUS提供的用户材料子程序UMAT，实现Chaboche黏塑性统一本构方程与ABAQUS程序的有机结合，为利用Chaboche黏塑性统一本构模型完成航空发动机结构强度评价和分析奠定基础。

3 结果与分析

图4给出了750 ℃不同应变速率条件下(1×10-3s-1和5×10-3s-1)的高Nb-TiAl合金单轴拉伸及有限元模拟曲线。从图4可以看出，施加的不同应变速率对材料的弹性阶段几乎没有影响，两组不同应变速率条件下的弹性拉伸数据几乎重合，而施加的不同应变速率对材料的屈服阶段影响明显，即随着施加应变速率的增加，材料发生屈服后的应力增加。以上试验表明，该高Nb-TiAl合金在750 ℃下具有明显的拉伸率相关性。另外，采用Chaboche黏塑性统一本构模型对高Nb-TiAl合金在750 ℃下的拉伸行为及率相关性进行了数值模拟计算，可以看出，Chaboche黏塑性统一本构模型能够准确模拟该材料的拉伸行为，同时也能对材料的拉伸率相关性进行准确表征。

图4 不同应变速率的单轴拉伸及有限元模拟曲线Fig.4 Experimental and simulated tensile data at different strain rates

图5给出了750 ℃不同应力水平条件下(360 MPa,380 MPa和420 MPa)的高Nb-TiAl合金蠕变及有限元模拟曲线。从图5可以看出，随着施加应力水平的增加，材料蠕变断裂寿命逐渐减小，材料发生蠕变断裂时的蠕变应变也逐渐减小，而稳态蠕变速率逐渐增加。对于应力水平为380 MPa和420 MPa的载荷状况，高Nb-TiAl合金的蠕变曲线仅包含初始蠕变和稳态蠕变两个典型阶段，而对于应力水平为360 MPa的载荷状况，高Nb-TiAl合金的蠕变曲线包含初始蠕变、稳态蠕变和加速蠕变三个完整阶段。采用Chaboche黏塑性统一本构模型对高Nb-TiAl合金在750 ℃下的蠕变行为进行了数值模拟计算，可以看出，Chaboche黏塑性统一本构模型能够准确模拟该材料的蠕变行为，能够对材料的初始蠕变、稳态蠕变和加速蠕变三个完整阶段进行准确表征。

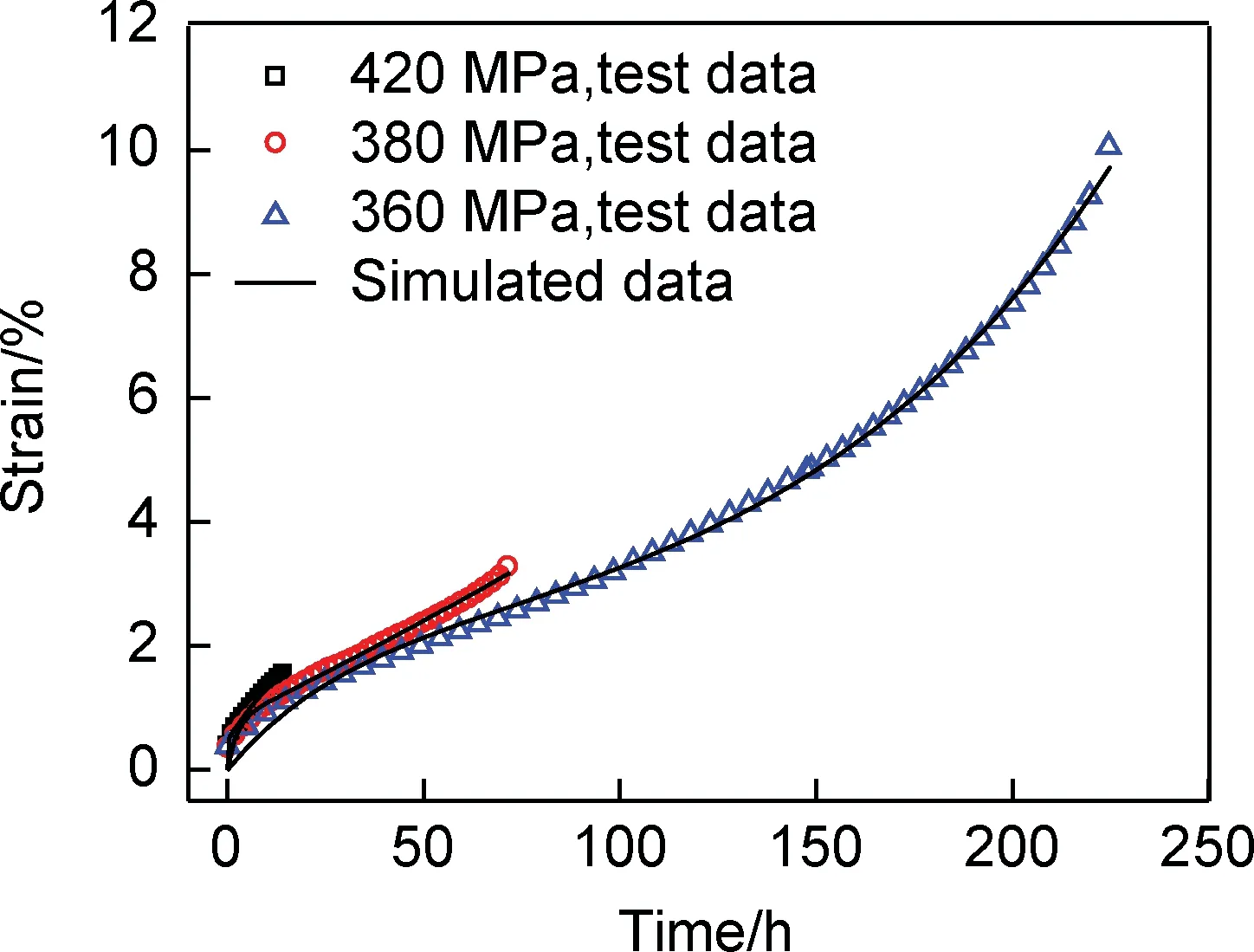
图5 不同应力下的蠕变及有限元模拟曲线Fig.5 Experimental and simulated creep data at different stresses

图6给出了750 ℃不同应变水平条件下(0.30%和0.35%)的高Nb-TiAl合金循环应力响应规律，主要考察了保载条件对材料循环应力响应的影响。从图中可以看出，不论是低周疲劳还是疲劳-蠕变交互试验条件，随着施加应变水平的增加，材料的循环应力增加，而断裂寿命减小。高Nb-TiAl合金循环应力响应规律因试验条件的不同而有所不同，对于高Nb-TiAl合金的低周疲劳试验而言，不同应变水平下的循环应力随着循环数的增加而增加，表现出明显的循环硬化现象，且硬化现象随着施加应变水平的增加而愈发明显。对于高Nb-TiAl合金的疲劳-蠕变交互试验而言，不论是上保载、下保载和是上下对称保载状态，不同应变水平下的循环应力随着循环数的增加而减小，表现出明显的循环软化现象。这是因为在疲劳试验应变峰谷处保持一定时间的应变恒定，可产生明显的应力松弛效应，从而产生循环软化现象。采用Chaboche黏塑性统一本构模型对高Nb-TiAl合金在750 ℃下的循环应力变化行为进行了数值模拟计算，可以看出，Chaboche黏塑性统一本构模型能够准确模拟该材料的循环应力响应，能够对材料的循环硬化和/或软化行为进行合理表征，虽然拟合曲线与试验数据存有一定的微小差距，但已完全满足材料工程化应用的需求。

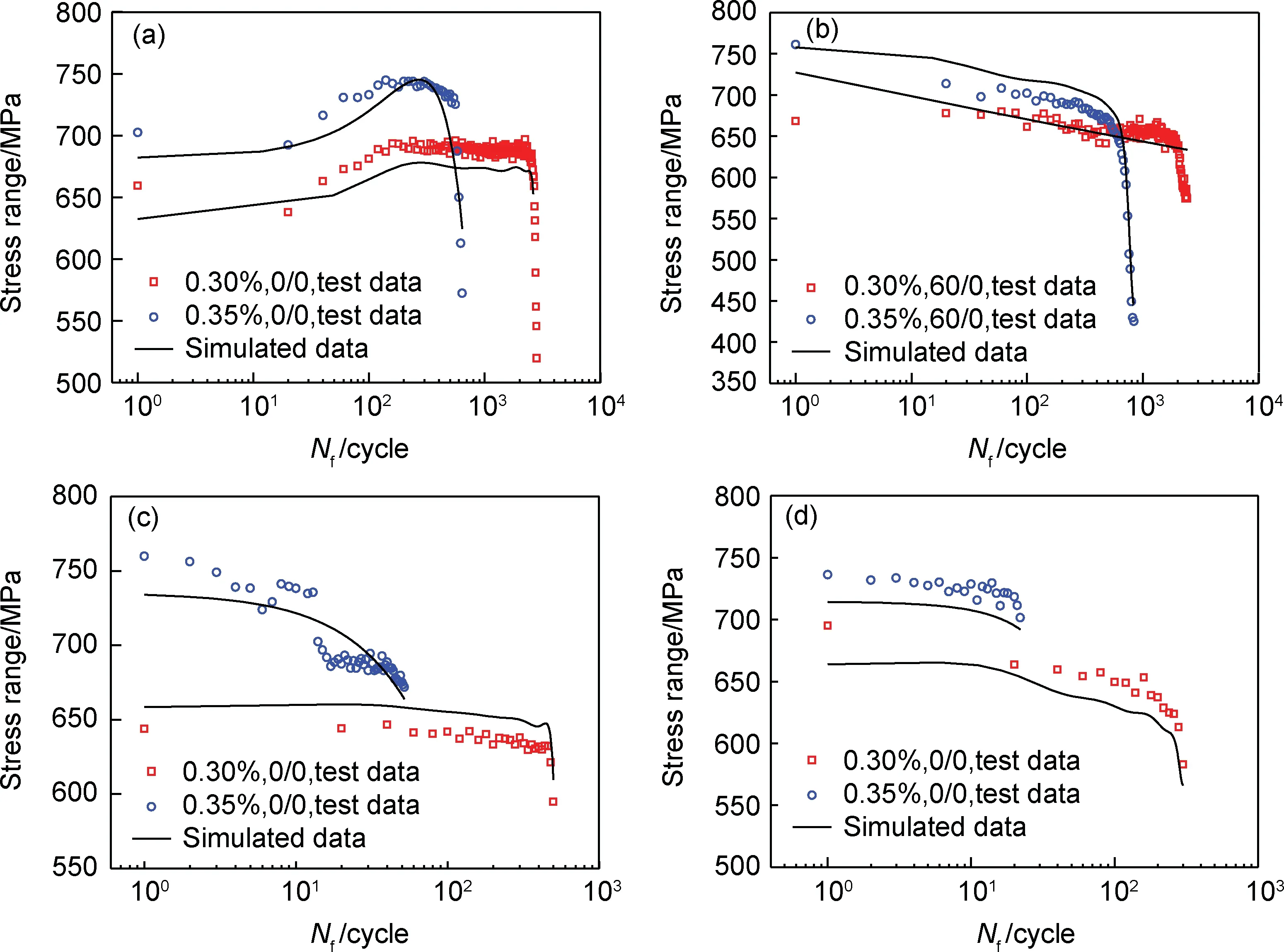
图6 不同应变条件下的应力范围随循环数变化的试验及有限元模拟曲线 (a)上保载60 s；(b)上下各保载30 s；(c)下保载60 s；(d)不保载Fig.6 Experimental and simulated stress range-cyclic life data at different strains (a)tensile dwell time 60 s; (b)balanced dwell time 30 s;(c)compressive dwell time 60 s;(d)no dwell time

图7给出了750 ℃不同应变水平条件下(即0.30%和0.35%)的高Nb-TiAl合金稳态迟滞回线响应规律，主要考察了保载条件对材料稳态迟滞回线响应的影响。从图7可以看出，不论是低周疲劳还是疲劳-蠕变交互试验条件，随着施加应变水平的增加，稳态迟滞回线的面积(即循环应变迟滞能)增加，且稳态迟滞回线的峰谷应力值也增加。对于无保载的低周疲劳和上下各保载30 s的疲劳-蠕变交互试验，稳态迟滞回线关于应力轴或应变轴基本上呈反对称结构，而对于上保载60 s和下保载60 s疲劳-蠕变交互试验，稳态迟滞回线分别沿着应力轴下移和上移，从而产生非零的平均应力。从疲劳-蠕变交互试验曲线可以看出，应力松弛发生在应变峰谷处的保持阶段。采用Chaboche黏塑性统一本构模型对高Nb-TiAl合金在750 ℃下的稳态迟滞回线进行了数值模拟计算，可以看出，Chaboche黏塑性统一本构模型能够准确模拟该材料的稳态迟滞回线，特别是能够准确模拟疲劳-蠕变交互试验下的稳态迟滞回线所反映出来的应力松弛现象。

图7 不同应变条件下的稳态迟滞回线的试验及有限元模拟曲线 (a)上保载60 s； (b)上下各保载30 s；(c)下保载60 s；(d)不保载Fig.7 Experimental and simulated stable hysteresis loops at different strains (a)tensile dwell time 60 s; (b)balanced dwell time 30 s;(c)compressive dwell time 60 s;(d)no dwell time

综上所述，本工作采用的Chaboche黏塑性统一本构模型能够准确模拟高Nb-TiAl合金的拉伸行为(率相关性)、蠕变行为(完整蠕变曲线三个阶段)、低周疲劳行为(循环硬化/软化现象)和疲劳-蠕变行为(应力松弛现象)，且模拟精度较高，为Chaboche黏塑性统一本构模型成功应用于航空发动机TiAl合金叶片的结构优化设计和强度校核提供了技术支撑。

4 结论

(1)通过对高Nb-TiAl合金750 ℃条件下的综合力学性能试验，获得了材料不同应变速率的单轴拉伸、低周疲劳、疲劳-蠕变交互和蠕变试验数据和曲线。

(2)采用自适应的显式Euler法将微分形式的Chaboche黏塑性统一本构模型离散为差分方程组，并植入到有限元软件ABAQUS的用户材料子程序UMAT，成功实现对高Nb-TiAl合金高温力学行为的有限元数值模拟仿真。

(3)宏观唯象Chaboche黏塑性统一本构模型耦合了蠕变损伤演化率并考虑了Ohno-Wang修正，使得该模型能够更加准确地表征和预测高Nb-TiAl合金的拉伸行为(率相关性)、蠕变行为(完整蠕变曲线三个阶段)、低周疲劳行为(循环硬化/软化现象)和疲劳-蠕变行为(应力松弛现象)，且模拟精度较高。

[1] NIEH T G, HSIUNG L M, WADSWORTH J. Superplastic behavior of a powder metallurgy TiAl alloy with a metastable microstructure [J]. Intermetallics, 1999, 7: 163-170.

[2] SONG L, LIN J P, LI J S. Effects of trace alloying elements on the phase transformation behaviors of ordered ω phases in high Nb-TiAl alloys [J]. Materials and Design, 2017, 113: 47-53.

[3] FANG L, LIN J P, LIANG Y F,etal. Microstructural instability in surface layer of a high Nb-TiAl alloy processed by shot peening following high temperature exposure [J]. Intermetallics, 2016, 78: 8-16.

[4] PATRIARCA L, FILIPPINI M, BERETTA S. Digital image correlation-based analysis of strain accumulation on a duplex γ-TiAl[J]. Intermetallics, 2016, 75: 42-50.

[5] CHEN G, PENG Y B, ZHENG G,etal. Polysynthetic twinned TiAl single crystals for high-temperature applications [J]. Nature Materials, 2016, 15: 876-881.

[6] ZHOU H T, KONG F T, WANG X P,etal. High strength in high Nb containing TiAl alloy sheet with fine duplex microstructure produced by hot pack rolling [J]. Journal of Alloys and Compounds, 2017, 695: 3495-3502.

[7] KARTAVYKH A V, ASNIS E A, PISKUN N V,etal. Room-temperature tensile properties of float-zone processed β-stabilized γ-TiAl(Nb,Cr,Zr) intermetallic [J]. Materials Letters, 2017,188: 88-91.

[8] ZHANG S Z, ZHANG C J, DU Z X,etal. Microstructure and tensile properties of hot fogred high Nb containing TiAl based alloy with initial near lamellar microstructure [J]. Materials Science and Engineering: A, 2015, 642:16-21.

[9] DING J, LIANG Y F, XU X J,etal. Cyclic deformation and microstructure evolution of high Nb containing TiAl alloy during high temperature low cycle fatigue [J]. International Journal of Fatigue, 2017, 99: 68-77.

[10] YU L, SONG X P, ZHANG M,etal. Effect of stress ratio on fatigue lifetime of high Nb containing TiAl alloy at elevated temperature [J]. Materials & Design, 2015, 84: 378-384.

[11] KRUML T, OBRTLK K. Microstructure degradation in high temperature fatigue of TiAl alloy [J]. International Journal of Fatigue, 2014, 65: 28-32.

[12] TIAN S G, LV X X, YU H C,etal. Creep behavior and deformation feature of TiAl-Nb alloy with various states at high temperature [J]. Materials Science and Engineering: A, 2016, 651: 490-498.

[13] TIAN S G, WANG Q, YU H C,etal. Microstructure and creep behaviors of a high Nb-TiAl intermetallic compound based alloy [J]. Materials Science and Engineering: A, 2014, 614: 338-346.

[14] ZHANG M, SONG X P, YU L,etal. In situ observation of fatigue crack initiation and propagation behavior of a high-Nb TiAl alloy at 750°C [J]. Materials Science and Engineering: A, 2015, 622: 30-36.

[15] CUI W F, LIU C M. Fracture characteristics of γ-TiAl alloy with high Nb content under cyclic loading [J]. Journal of Alloys and Compounds, 2009, 477: 596-601.

[16] WU Z, HU R, ZHANG T B,etal. Microstructure determined fracture behavior of a high Nb containing TiAl alloy [J] . Materials Science and Engineering: A, 2016, 666: 297-304.

[17] CHABOCHE J L. Development of continuum damage mechanics for elastic solids sustaining anisotropic and unilateral damage [J]. International Journal of Damage Mechanics, 1993, 2: 311-329.

[18] PERZYNA P. The constitutive equations for rate sensitive plastic materials [J]. Quarterly Journal of Applied Mathematics, 1963, 20: 321-332.

[19] PERZYNA P. Fundamental problems in viscoplasticity[J]. Advances in Applied Mechanics, 1966, 9: 243-377.

[20] LEMAITRE J, CHABOCHE J L. Mechanics of solid materials [M]. New York： Cambridge University Press, 1990.

[21] RABOTHOV Y M. Creep problems in structural members [M]. Amsterdam: North-Holland, 1969.