单晶γ-TiAl合金疲劳裂纹扩展机制的原子模拟

张 玲， 罗德春， 白湘霞， 芮执元

(1.兰州工业学院 甘肃高校绿色切削加工技术及其应用重点实验室，兰州 730050； 2.兰州理工大学 机电工程学院，兰州 730050； 3.玉门油田分公司机械厂，甘肃 玉门 735009)

TiAl 基金属间化合物晶体中因金属键与共价键共存，同时兼具金属的韧性及陶瓷的高温性能，故其具有高的比强度﹑比模量﹑良好的抗氧化性﹑抗蠕变性和优良的高温强度以及低密度等特性，是一类很有发展前途的高温结构材料[1]，然而室温脆性却限制了它的发展和应用。为解决此问题，材料界对其显微组织与力学性能的关系进行大量的实验研究[2-3]，主要集中在制备方法和热处理工艺对TiAl合金显微组织和性能的影响上[4-5]。经研究发现，相同显微组织和性能的材料，在经受不同载荷方式加载时，所表现出的断裂机理不尽相同。研究结果表明，加载时的不同控制方式对TiAl基合金的损伤及断裂有重要影响，且对其机理的影响也完全不同[6-8]。为了从微观结构上进一步探索微观缺陷在加载过程中的成因及演化规律，分子动力学方法成为理论研究者最有力的工具之一。Xu等[9]用分子动力学研究了TiAl金属化合物在位错反应中点缺陷的形成过程。通过分子动力学模拟显示出在剪切变形中，单一滑移系的运动即能促使空位、位错线及位错环的形成，且间隙原子显示出较强的运动能力，点缺陷与位错的反应程度很大程度取决于缺陷的性质以及滑移面之间的距离，位错反应也是许多点缺陷生成的来源。Tang等[10]采用分子动力学模拟了γ-TiAl单晶的空洞开裂过程。结果表明：位错核的连续产生和剪切循环的扩展使得空洞开裂，初始屈服强度随着试件尺寸和空洞体积分数的增加而减小，随着应变率的增加而增加。罗德春等[11-12]对γ-TiAl合金中心裂纹扩展及孔洞缺陷的位置效应进行了研究，发现无孔洞时，裂纹以脆性解理方式快速扩展至材料断裂，存在距中心裂纹不同位置孔洞时，对裂纹扩展形式及微观机理都有很大影响。在晶向对裂纹扩展影响的研究中发现，三种典型晶向下，裂纹扩展的过程及微观形变机制也完全不同。

材料无论是在生产过程还是实际运用中都会存在各种缺陷，而裂纹(尤其内部裂纹)是最主要的缺陷之一，它将导致TiAl合金材料抗疲劳和断裂性能降低，使零件在服役条件下的寿命急剧下降。截至目前,已有关于γ-TiAl合金分子动力学的研究主要集中在温度、加载速率、裂纹空洞剪切变形、拉伸变形和相变行为等方面，尚无发现施加循环交变载荷方式对该材料进行疲劳裂纹扩展的研究。因此，本工作从原子尺度出发，运用LAMMPS分子动力学软件计算γ-TiAl合金疲劳裂纹演化过程的应力值，通过OVITO软件对LAMMPS软件计算结果进行分析和可视化处理，研究交变载荷循环加载方式对单晶TiAl合金性能及裂纹扩展的影响，以研究TiAl合金的疲劳性能、裂纹扩展与组织形态的关系，从而弥补对TiAl合金研究的不足。

1 模型与模拟

1.1 模型建立

γ-TiAl合金的晶体结构是L10型面心四方(fct)，其原子结构如图1所示。其中分别以晶向[100]，[010]，[001]作为x，y，z三个坐标轴。

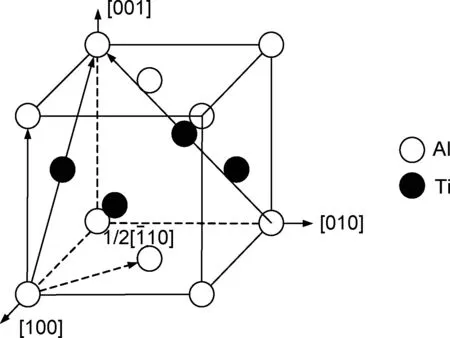
图1 γ-TiAl的L10结构Fig.1 L10 structure of γ-TiAl

图2 几何模型(a)和初始原子模型剖面图(b) Fig.2 Geometric model(a) and profile map of atomic model(b)

1.2 模拟过程

(1)

2 结果与分析

图3 时间-应力曲线图Fig.3 Curve of time -stress

图4 Stage1时间-应力曲线图Fig.4 Time-stress curve of stage 1

2.1 弹性变形阶段

初始阶段(Stage 1)，随着应变的增加，拉伸阶段应力线性增加速率基本相同，压缩阶段应力线性减小速率也基本相同(如图4)。直至t=25.68 ps，模型总能量因集聚而快速增大，内部晶格排列保持不变，弹性驰豫能及断键能组成的陷阱势垒使该应力状态下的裂纹难以穿过陷阱势垒，裂纹保持稳定，如图5(a)所示(以4个单位厚度面截取得到剖面图)。

随着模型加载的进行，观察模拟过程t=28.8 ps时发现，当内嵌裂纹尖端局部集中应力达到原子间作用力最大值时，即外加载荷高于Griffith加载时，裂纹上、下表面原子的原子键被拉断，裂纹尖端的上、下两端原子被从尖端推向远离尖端，预示着裂尖原子状态由有序到无序转变，应力感应变化呈现非线性关系，裂尖原子状态如图5(b)所示(以4个单位厚度面截取得到剖面图)，内部裂纹尖端面原子键陆续断裂，晶格出现不连续现象，裂纹尖端驰豫并伴随有钝化，裂纹扩展停滞。该行为被认为是原子间相互作用的非线性结果[16]，如图4(Stage 1放大部分)所示。晶格的不连续性呈现出裂纹陷阱效应[17],当内部裂纹尖端钝化时，其扩展进一步受阻而停滞，此时裂纹进入裂纹陷阱区域，裂纹陷阱能够保持裂纹稳定并阻止裂纹开裂。随着载荷的逐步增加，至t=35.84 ps，应力值达到屈服极限7.27 GPa时，裂纹陷阱势垒被克服后，裂纹失稳从而导致向模型表面迅速扩展。扩展过程中，可以观测到裂纹前端只有少量的变形，没有位错发射，裂纹呈现脆性解理扩展特征。反向压缩载荷因加载时间短，仅抑制内、外部裂纹解理扩展速率而未促使其他微观结构特征出现。

图5 不同时刻的原子状态图Fig.5 Atomic figure at different time (a)t=25.68 ps;(b)t=28.8 ps

2.2 快速塑性变形阶段

图6～图7为塑性变形阶段(Stage 2)四个循环加载应力-应变曲线图及典型内部微观结构演化图。

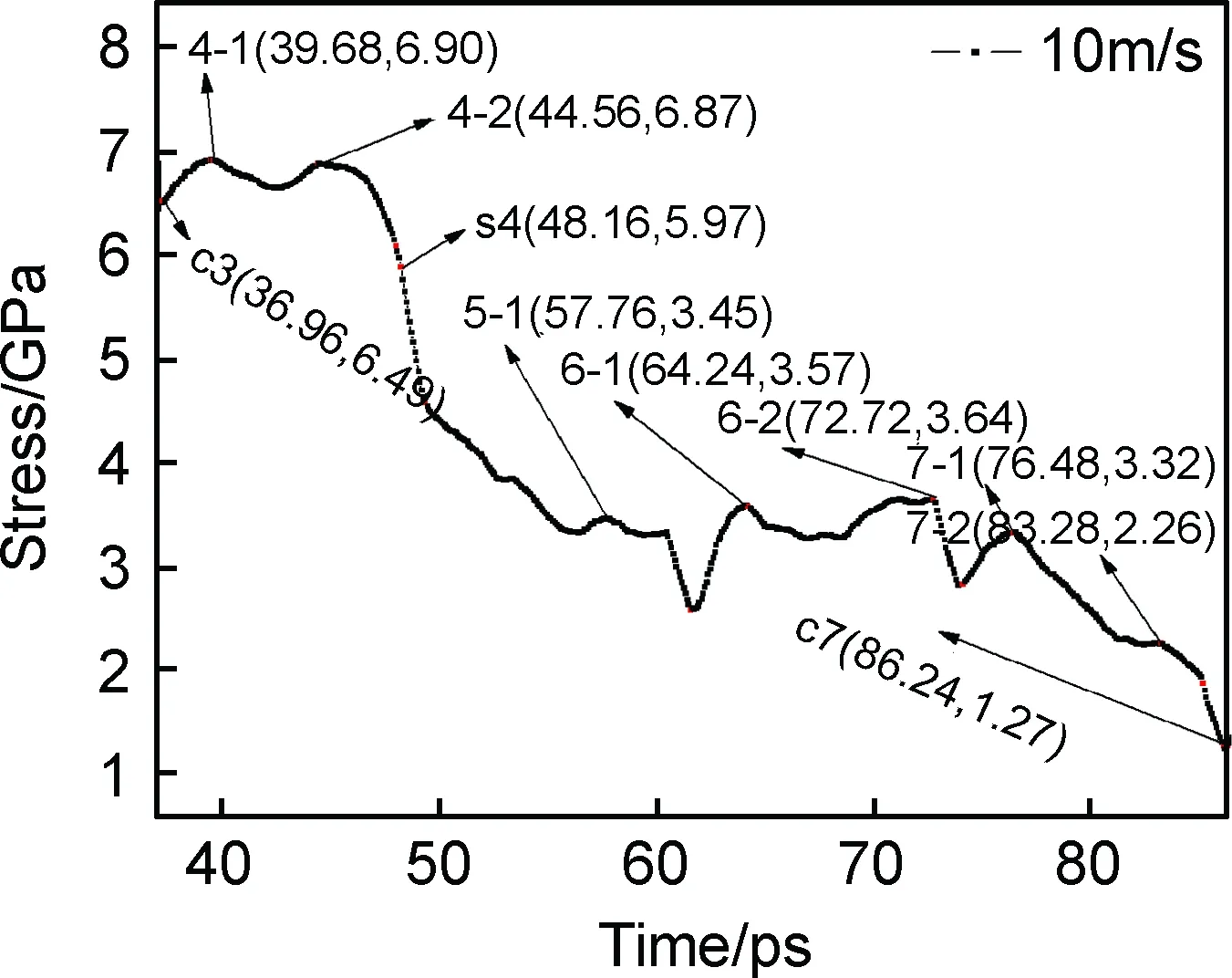
图6 Stage 2时间-应力曲线图Fig.6 Time-stress curve of Stage 2

随着加载的进行，裂尖继续发射位错并滑移至边界而塞积、形核，基于Lomer-Cottrell stair-rod锁朝[111]方向不断产生许多面状堆垛层错，紧接着更多堆垛层错带、压杆位错及其他复杂反应也介入其中，裂尖开始迅速钝化，当t=57.76ps时，体系应力到达短期峰值。因裂尖钝化能降低裂纹尖端应力，裂纹从原来的裂纹平面跳跃至新的裂纹平面，裂纹前缘偏离初始方向，裂纹尖端的钝化促使裂纹张开，形变进一步增大，裂纹变得越来越宽，韧性有所提高。裂纹尖端钝化后，将降低拉伸加载作用下堆积在裂纹尖端处的局部集中应力，使裂纹尖端处的局部集中应力重新分布，局部最大应力的方向逐渐脱离裂尖，慢慢移向偏离裂纹面30°顶角处，对于此时的裂纹来说，很难沿垂直于主拉伸正应力的原始裂纹平面方向扩展，而是选择沿着拉伸局部应力强度因子取最大值，裂纹陷阱势垒相对小的路径扩展[18]，这一裂纹扩展法则使微裂纹在拉压循环加载作用下逐渐产生取向效应，主裂纹扩展方向出现30°偏折，并且整个体系其他区域产生包括空位团簇等各种缺陷(如图7(c))，体系应力迅速下降(如图6)。

图7 不同时刻的原子状态图Fig.7 Atomic figure at different time (a)t=39.68 ps;(b)t=44.56 ps;(c)t=57.76 ps; (d)t=64.24 ps;(e)t=72.72 ps;(f)t=76.48 ps;(g)t=85.28 ps

在整个缺陷形成与扩展过程中，裂尖持续发射大量棱柱位错并积聚与形核，当t=64.24 ps时，应力达到阶段峰值3.57 GPa，此后位错发射节奏减缓，堆垛层错生成及滑移数量明显减少，裂纹缓慢扩展，应力呈递减状态(如图7(d))。当t=72.72 ps时，随着位错加快发射、塞积，形核的速率逐渐增大，体系应力再次达到阶段峰值3.64 GPa时，微裂纹向偏折方向开始扩展，并在位错形核处形成微空洞，此时空洞周围开始出现大量棱柱位错的发射，体系应力重新分布，呈迅速递减状态，进入反向压缩阶段，微孔洞周围位错发射受到压制，微孔洞顶角坍塌变形(如图7(e))。

当进入第七个循环加载t=76.48 ps后，模型形变过程相对平稳，裂尖塑变区域逐渐增大，未观察到位错发射，位错形核持续增大且伴有更多微空洞产生，位错塞积形核区与裂尖塑变区域联通，微观形变主要以堆垛层错滑移为主，产生大量堆垛层错带，位错形核处大量空洞积聚演变成近椭圆形孔洞，模型其他区域出现各种缺陷，体系应力达到3.32 GPa(如图7(f))。进入压缩加载阶段后，观察到堆垛层错滑移数量减少，滑移速度减缓，应力开始减小(如图7(g))。

2.3 均匀塑性变形阶段

图8和图9为均匀塑性变形阶段(Stage 3)三个循环加载应力应变曲线图和典型内部微观结构演化图。该阶段应力应变曲线图整体呈现锯齿状，在每个循环加载周期内应力-应变曲线均呈现典型“M”状。

图8 Stage 3时间-应力曲线图Fig.8 Curve of time -stress with Stage 3

图9 不同时刻的原子状态图Fig.9 Atomic figure at different time (a)t=88.72 ps;(b)t=89.04 ps;(c)t=91.76 ps;(d)t=95.2 ps;(e)t=97.44 ps

加载初期，裂纹扩展几乎停滞，可观察到裂尖发射少量滑移位错并在模型边界处塞积，裂纹面变宽。拉伸加载与热激活能未能突破位错塞积阻力及裂纹陷阱势垒，位错发射停止，当t=88.72 ps时，随着拉伸应力不断叠加，裂尖原子错排进一步加剧，钝化现象更加严重，裂纹面应力重新分布，局部应力集中分布在裂尖，位错塞积处孔洞演变成圆形并逐渐扩大(如图9(a))。直至t=89.04 ps时，清楚地观察到裂尖前端塑性变形区域开始形成微孪晶(如图9(b))，并向位错形核区缓慢移动，体系应力开始下降，此后微孪晶及堆垛层错滑移为主要形变机制。到t=91.76 ps时，裂尖塑变区与位错形核区通过微孪晶运动完全联通(如图9(c))，此时堆垛层错、位错、微孪晶等各种缺陷相互作用明显加剧，体系应力开始集聚并攀升，模型各个区域充斥各种缺陷(如图9(d))。当进入t=97.44 ps压缩加载后可以看到，裂纹开口度减小，以孔洞周围已经形成的位错核为源，棱柱位错开始形成并迅速滑移，在压力的作用下很快形成大量层错结构和大面积层错区，孔洞周围缺陷明显减少，应力重新分布后集中在孔洞周围，孔洞坍塌变形后向微裂纹缺陷演变(如图9(e))。纵观后续循环加载过程，其形变机制及微观形变过程与之相似。可以设想，经多次循环加载后，终将以主裂纹与孔洞演化而成的子裂纹相连而断裂。

3 结论

(1)弹性变形前阶段(Stage 1)，拉伸加载应力-应变曲线呈线性递增，压缩阶段呈线性递减趋势，内嵌裂纹面保持理想晶格状态。末尾阶段达到启裂应力之6.59 GPa后，拉伸加载及热激活促使内嵌裂纹迅速以脆性解理扩展形式向模型表面失稳扩展，压缩加载减缓了裂纹扩展速度。

(2)快速塑性变形阶段(Stage 2)，拉伸加载阶段，少量裂尖原子首先脱离，形成间隙原子及空位团簇缺陷，裂尖钝化后扩展速度缓慢但出现30度偏折，开口度逐渐增大，位错快速发射，前端塑性变形区快速增大，整个阶段以棱柱位错滑移，堆垛层错开动为主要塑变形式，Lomer-Cottrell位错是模型主要的塑变强化机制，压缩载荷抑制了位错、层错发射及减缓了其运动速度，在裂尖塑性变形区加速了空位的产生及积聚成空洞。

(3)均匀塑性变形阶段(Stage 3)，拉伸加载初期，裂纹扩展几乎停滞，应力集中分布在裂尖及塑变区，裂尖发射少量棱柱位错后迅速发生微孪晶现象，位错滑移，堆垛层错开动及裂尖区域微孪晶为主要塑性变形形式，压缩加载导致发射位错减少及减缓了层错开动速度，加速孔洞坍塌过程。

[1] CHEN J H， CAO R， WANG G Z，etal．Study on notch fracture of Ti Al alloys at room temperature [J]．Metallurgical and Materials Trans A，2004，35(2)：439-457．

[2] LU Y H， ZHANG Y G， CHEN C Q．The fracture mechanism of a fully in fully lamellar γ-alloys through in-situ SEM observation[J]．Intermetallics，2000(8)：1443-1445．

[3] 郑瑞廷， 张永刚， 陈昌麟， 等． 显微组织应变速率对全片层Ti Al 合金室温塑性的影响[J]．材料科学与工艺，2004，12(03)：225-229．

(ZHENG R T,ZHANG Y G,CHEN C Q,etal.The effect of microstructure and strain rate on the ambient ductility of FL TiAl alloys[J]. Materials Science & Technology, 2004,12(3)：225-229．)

[4] 孙红亮 ，黄泽文 ，朱德贵．热处理对 Ti-44A1-4Nb-4Zr-1B 合金组织和性能的影响[J]．热加工工艺 2013，42(1)：187-192．

(SUN H L, HUANG Z W, ZHU D G. Effects of heat treatment on microstructure and mechanical properties of TiAl-based alloy[J]. Hot Working Technology, 2013,42(1):187-192．)

[5] 孙诗涵， 陈华．TiAl合金高温真空烧结组织及氧化性能研究[J]．热加工工艺, 2014，43(6)：1-4．

(SUN S H , CHEN H.High temperature vacuum sintering microstructure and oxizability of TiAl alloy[J]. Hot Working Technology, 2014,43(6):1-4．)

[6] 朱浩，曹睿，陈剑虹，等．不同预损伤对层状 TiAl基合金断裂行为的影响[J]．稀有金属，2006，32(3)：60-65．

(ZHU H,CAO R, CHEN J H,etal. Effect of different pre-damage on fracture behavior of lamellar titanium aluminum alloys[J]. Chinese Journal of Rare Metals, 2006,32(3):60-65．)

[7] 雷明霞 ，曹睿 ，陈剑虹 ，等．加载速率对 Ti Al 基合金载荷控制下的断裂机理影响[J]． 稀有金属材料与工程， 2006，35(11)：1730-1734．

(LEI M X,CAO R,CHEN J H,etal.Effect of loading rate on fracture mechanism of TiAl-Based alloys[J]. Rare Metal Materials and Engineering, 2006,35(11):1730-1734．)

[8] 曹睿，陈剑虹，张继，等．近全层 γ-TiAl基合金室温拉伸断裂机理的研究[J]． 稀有金属材料与工程，2005，34(5)：696-700．

(CAO R, CHEN J H, ZHANG J,etal.Study on tensile fracture mechanisms of γ-TiAl alloys for near fully-lamellar microstructure at room temperature[J]. Rare Metal Materials and Engineering, 2005,34(5):696-700.)

[9] XU D S , WANG H, YANG R ,etal. Point defect formation by dislocation reaction in TiAl[J]. Materials Science and Engineering, 2009, 3(1): 1-6.

[10] TANG F L, CAI H M, BAO H W,etal. Molecular dynamics simulations of void growth in γ-TiAl single crystal[J]. Computational Materials Science, 2014, 84: 232-237.

[11] 罗德春,芮执元,付蓉,等.单晶γ-TiAl合金中裂纹沿[111]晶向扩展的分子动力学研究[J]. 功能材料, 2016，47(2) ：2067-2071.

(LUO D C,RUI Z Y,FU R,etal.Molecular dynamics researvh of crack propagation along the [111] orientation in single crystal γ-TiAl[J]. Journal of Functional Materials， 2016,47(2):2067-2071.)

[12] 罗德春,芮执元,付蓉,等.单晶γ-TiAl中孔洞位置对裂纹扩展影响的分子动力学模拟[J].功能材料,2016，47(6)：6136-6141.

(LUO D C,RUI Z Y,FU R,etal.Effect of holes position on single crystal γ-TiAl alloy crack propagation based on molecular dynamics simulation[J]. Journal of Functional Materials, 2016,47(6):6136-6141.)

[13] ZOPE R R, MISHINY. Interatomic potentials for atomistic simulations of the Ti-Al system[J]. Phys rev B, 2003, 68(2):366-369.

[14] 曲洪磊,王宇,夏源明，等.γ-TiAl 单晶纳米杆拉伸变形的分子动力学研究[J]. 中国科学技术大学学报, 2009, 39(6): 627-630.

(QU H L,WANG Y, XIA Y M,etal. Molecular dynamics study on tension deformation of nano-single crystal γ-TiAl intermetallics[J]. Journal of University of Science and Technology of China, 2009,39(6):627-630.)

[15] TANG F L, CAI H M, BAO H W,etal. Molecular dynamics simulations of void growth in γ-TiAl single crystal[J]. Computational Materials Science, 2014, 84: 232-237.

[16] ANDREA P, ROBIN C B．Relation between driving energy,crack shape，and speed in brittle dynamic fracture[J]．Phys Rev B, 2005，72：54101-54111．

[17] THOMSON R, HSIEH C, RANA V. Lattice trapping of fracture cracks[J].Appl Phys, 1971,42: 3154-3160．

[18] DIENES G J ,PASKIN A .Molecular dynamic Simulations of crack ,KM progagation [J].Phys Chem Solid, 1987，48:1015-1033.