基于车辆动力学的道路坡度与整车质量估计

戴卓 吴光强,2

（1.同济大学，上海 201804；2.东京大学 生产技术研究所，东京 153-8505）

1 前言

传统的自动变速器二参数换挡规律仅根据车速和加速踏板开度确定换挡点，存在较大局限性，且制定二参数换挡规律时通常仅考虑平路行驶工况，在上坡行驶工况可能出现循环换挡现象，造成换挡执行元件的反复作用，在下坡行驶工况可能由于驾驶员松开加速踏板或车速暂时升高导致升挡，无法充分利用发动机辅助制动作用，还增加了制动器的工作负担，尤其是下长坡时容易导致制动器过热失效。因此，有必要在车辆行驶过程中获取实时的道路坡度信息，实现适应不同道路坡度的自动变速器智能控制。

整车质量和道路坡度是自动变速器换挡控制中的两个重要参数，可通过运动学估计、动力学估计等方法得到。Sahlholm[[11]]为试验车辆加装了GPS传感器，通过差分算法获取实时的道路坡度信息；金辉[[22]]为试验车辆加装了加速度传感器，通过计算汽车坡道行驶时纵向车速差分值与纵向加速度传感器数值之差，查表得到道路坡度的近似值；赵治国[[33]]根据整车纵向动力学方程，采用最小二乘法对整车质量和道路坡度进行了估计；Wrag⁃ge-Morley[4]采用自适应非线性观测器，实现了基于动力学模型的道路坡度估计；Kidambi[5]加装了半轴转矩传感器、纵向加速度传感器，通过试验比较了扩展卡尔曼滤波、最小二乘法、线性观测器等方法的坡度估计效果。

本文基于变速器动力学模型和整车纵向动力学方程，运用卡尔曼滤波和改进型递推最小二乘法，在不加装传感器的前提下实现了对整车质量和道路坡度的实时估计。

2 道路坡度与整车质量估计算法

2.1 整车纵向动力学方程

根据牛顿第二定律，得到整车纵向动力学方程：

式中，m为整车质量；ax为纵向加速度；Fw为驱动力，Fi为坡道阻力，Ff为滚动阻力，Faero为空气阻力。

根据汽车理论的相关公式，整车纵向动力学方程可写为：

式中，Ts为变速器输出轴转矩；r为车轮滚动半径；g为重力加速度；α为坡度角；f为滚动阻力系数；ρ为空气密度；Cd为空气阻力系数；A为迎风面积；vx为纵向车速；r、ρ、Cd、A、g均为常数。

vx可从CAN总线上读取，ax可通过对纵向车速微分得到，在半轴或轮胎处加装转矩传感器可得到较为精确的变速器输出轴转矩，但是会大幅度增加成本，难以在量产车上得到实现。部分研究采用式（3）估计变速器输出轴转矩Ts：

式中，Te为发动机输出转矩；ig为当前挡位传动比；i0为主减速器传动比；ηT为变速器传动效率。

实际上ηT会随变速器挡位、发动机转速等参数变化，难以通过理论分析或试验得到不同工况下的ηT准确值，因此式（3）容易带来较大误差。基于上述考虑，通过建立变速器动力学模型，采用卡尔曼滤波方法实时估计变速器输出轴转矩。

2.2 变速器动力学模型

本文研究对象是某装配7速双离合自动变速器（DCT）的乘用车。定义参数i1～i7分别为1～7挡传动比，ia1和ia2分别为中间轴1和中间轴2与输出轴间的主减速比，Ie为发动机输出轴转动惯量，Ic1为离合器1从动盘、输入轴1及轴上齿轮对的等效转动惯量之和，Ic2为离合器2从动盘、输入轴2及轴上齿轮对的等效转动惯量之和，Im1、Im2分别为中间轴1、中间轴2的转动惯量，Te、Tc1、Tc1、Ts分别为发动机输出轴、离合器1从动盘、离合器2从动盘和变速器输出轴传递的转矩，ce、cc1、cc2、cm1、cm2、cs分别为发动机输出轴、输入轴1、输入轴2、中间轴1、中间轴2、变速器输出轴的旋转阻尼系数，ωe、ωc1、ωc2、ωs分别为发动机输出轴、离合器1从动盘、离合器2从动盘和变速器输出轴的转速。

以1挡稳定行驶为例，假设各齿轮对传动效率均为η，则1挡稳定行驶时的动力学方程：

1挡稳定行驶时离合器1结合，离合器2完全分离，变速器各轴转速满足以下关系：

ωs较难直接获取，而发动机转速ωe可直接从CAN总线中读取，将式（4）整理为ωe的关系式：

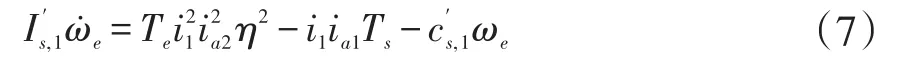
上述方程均未考虑同步器的转动惯量及动态特性，也没有考虑同步器预换挡对大小的影响，故DCT车辆保持n(n=1,2,…,7)挡行驶时，对应的等效转动惯量和等效旋转阻尼系数可视为常数。

设采样周期为dt，将式（7）离散化得到：

假设系统噪声均为互相独立的高斯白噪声，过程噪声向量为Wk，测量噪声向量为Vk，为方便建立DCT传动系统状态方程，假设发动机输出转矩和变速器输出轴转矩的瞬时变化速率较小，即Te≈0,Ts≈0，基于上述假设及式（8）得到1挡稳定行驶时的系统状态方程和测量方程：

车辆在其他挡位稳定行驶时，均能得到类似的系统状态方程。

2.3 卡尔曼滤波算法

卡尔曼滤波算法包括以下5个部分，

c. 计算滤波增益矩阵Kk：

式中，Φ为系统状态转移矩阵；H为系统观测矩阵；Qk、Rk分别为过程噪声协方差矩阵和测量噪声协方差矩阵。

根据式（9）和式（10）描述的DCT系统状态方程，采用卡尔曼滤波算法可得到变速器输出轴转矩的实时估计值进行道路坡度与整车质量估计时，将作为估计算法的输入。

2.4 最小二乘估计算法

将整车纵向动力学方程改写成向量乘积形式：

最小二乘法是经典的参数辨识方法，在许多实际问题中得到了广泛的应用，其基本原理如下，参数估计的误差成本函数J为：

误差成本函数J越小，参数θ的估计效果越好，使J取最小值的估计值即为θ的最小二乘估计值，此时J对θ的偏导为0，整理得到最小二乘估计表达式：

表1 遗忘因子λ对参数估计结果的影响

加入遗忘因子的RLS估计算法虽然能实现对时变参数的估计，但是该算法假设所有待估计参数均是同步变化的，车辆实际行驶时整车质量可视为定值，而坡度的时变特性较明显，若对所有参数的估计均采用同一个遗忘因子，估计算法将按照同一规律对时变参数（坡度）和非时变参数（质量）同时进行校正，造成较大误差。文献[6]提出了采用多个遗忘因子的改进型递推最小二乘估计方法，对于二参数估计问题，设待估计参数为θ1和θ2，遗忘因子为λ1和λ2，则误差成本函数J为：

因此，基于式（16）～式（19）描述的整车纵向动力学方程，可利用式（22）～式（29）改进型RLS算法实时估计1/m和sinα+fcosα。其中，sinα+fcosα为等效坡度[7]，表示路面滚动阻力和道路坡度对行驶阻力的贡献，当滚动阻力系数f已知时，可得出实际坡度。

2.5 估计算法流程

设计的实时估计算法流程如图1所示。

图1 实时估计算法流程

考虑到停车后总质量可能发生变化，设计在停车时停止运行算法并清空历史数据，将当前时刻的估计参数作为下次估计的初始值。

3 仿真验证

在MATLAB/Simulink中建立DCT车辆的纵向动力学模型，用于验证采用上述整车质量与道路坡度估计算法的可行性。为了充分利用历史数据得到准确的整车质量估计值，质量估计的遗忘因子在本次仿真中取1.05，由于道路坡度具有较明显的时变特性，故坡度估计的遗忘因子在本次仿真中取0.8，假设仿真过程中滚动阻力f为常数。仿真得到的结果如图2、图3所示。

图2 坡度估计仿真计算结果

图3 质量估计仿真计算结果

由仿真结果可知，建立的估计算法可较好地跟踪坡度变化，坡度估计值在仿真时间的第0.3 s、2.6 s、5.2 s和8.0 s出现了较大波动，这是因为在这些时刻发生了换挡操作，换挡过程中仿真模型变速器输出轴转矩出现了较大波动，整车质量估计值很快收敛且与实际值的误差很小。

4 试验验证

4.1 试验方案

为了验证所开发的整车质量与道路坡度估计算法效果，采用图4所示的流程进行实车试验。

试验车为搭载7速湿式DCT的乘用车，在平整路段行驶时开始记录数据，之后进入一段坡度为8%的试验坡道，通过坡道后继续在平整路面行驶一段时间后停止记录数据。估计算法所需的车速、发动机转矩、发动机转速等数据均通过采集CAN总线信号得到，采集装置的采样周期为0.02 s。

图4 试验流程

由于建立的DCT动力学方程未考虑换挡过程，无法准确估计换挡过程的变速器输出轴转矩值，在上述试验数据采集过程中DCT设为手动模式，保持挡位为2挡，且驾驶员全程没有踩下制动踏板。试验车的真实质量由整备质量与试验人员、试验设备的质量之和得到，图5为试验过程采集到的部分数据。

4.2 试验结果分析

采用图1所示的估计算法流程对试验数据进行处理，试验结果分析用到的部分参数如表2所示，图6为利用卡尔曼滤波算法估计得到的变速器输出轴转矩，图7和图8为本次试验的坡度、质量估计结果。

本次估计中整车质量和道路坡度的遗忘因子分别取1.01和0.4，试验车整备质量为1 365 kg，故整车质量估计的初始值取1 300 kg，对整车质量的估计在10 s内逐渐收敛，最终整车质量估计值为1 495 kg，而试验车的真实质量为1 504 kg，可见该算法对整车质量的估计效果较为理想。对道路坡度的估计虽然存在一定误差和较大噪声，但是估计值与实际道路坡度值基本吻合，能及时反映实际道路坡度的变化趋势，对自动变速器坡道换挡控制等具有较好的参考作用。

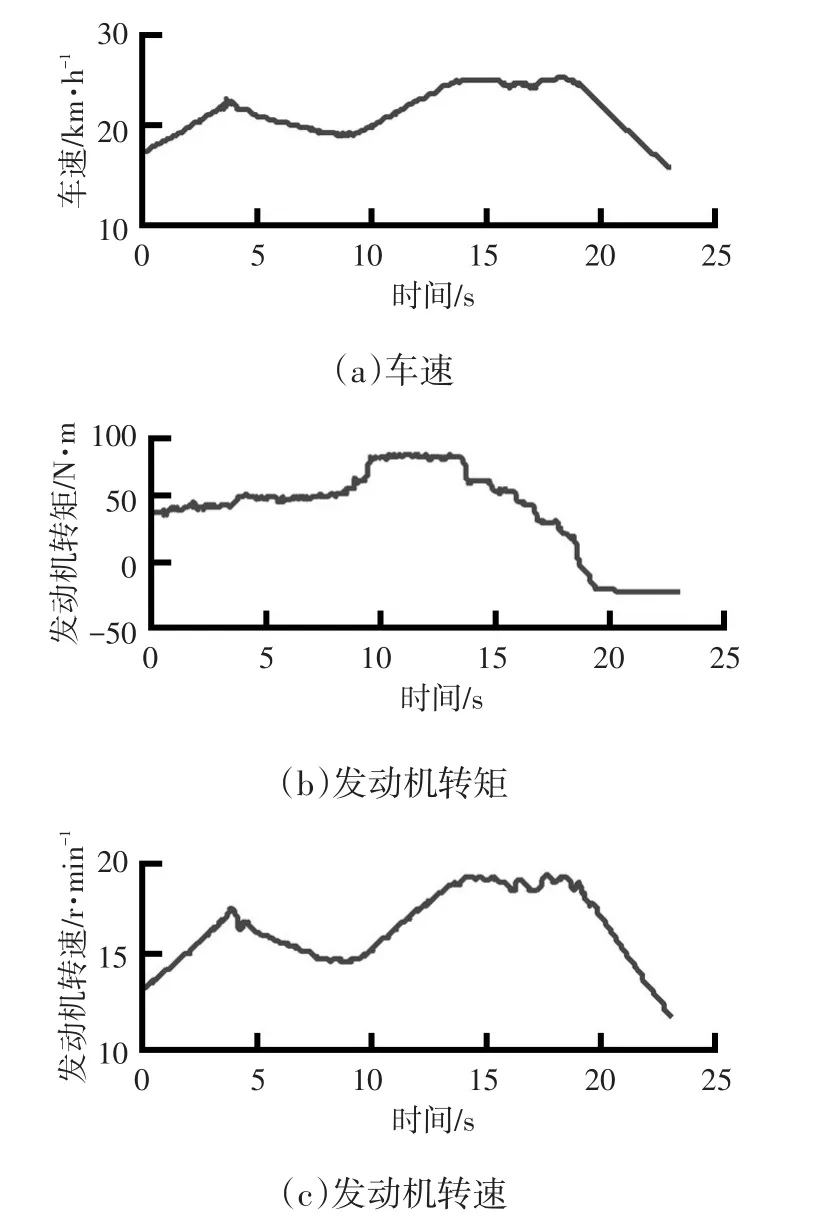
图5 上坡路段试验数据

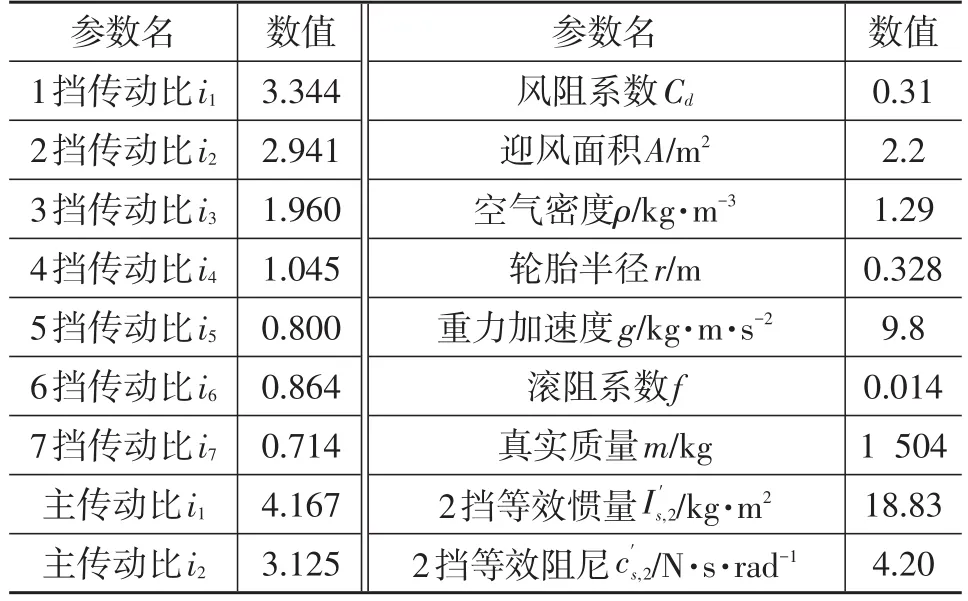
表2 试验基本参数

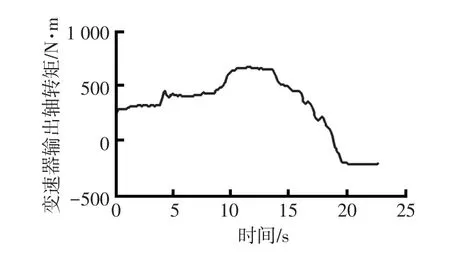
图6 变速器输出轴转矩估计值

图7 道路坡度估计试验结果

图8 整车质量估计试验结果

5 结束语

建立了7速DCT动力学模型，并采用卡尔曼滤波算法对变速器输出轴转矩进行实时估计，基于整车纵向动力学模型，开发了运用改进型递推最小二乘法的道路坡度与整车质量估计算法。设计的估计算法仅需采集CAN总线信号，不必加装GPS、半轴转矩传感器、加速度传感器等设备，提供了成本低廉的道路坡度与整车质量估计方法。仿真和试验验证结果表明，所开发的道路坡度与整车质量估计算法具有较好的估计效果，估计结果可供自动变速器换挡控制和自适应巡航等系统使用。

[1]Sahlholm P,Gattami A,Johansson K H.Piecewise Lin⁃ear Road Grade Estimation[C]//SAE 2011 World Con⁃gress and Exhibition,Detroit,12 April 2011.SAE inter⁃national,2011.

[2]金辉,李磊,李斌虎,等.基于加速度区间判断的坡道识别方法[J].中国公路学报,2010,23(1)：122-126.

[3]赵治国,王琪,刁威振,等.双离合器变速汽车坡道模糊修正换挡研究[J].中国机械工程,2013(15)：2122-2129.

[4]Wragge-Morley R, Herrmann G, Barber P,et al.Gradient and Mass Estimation from CAN Based Data for a Light Passenger Car[J].SAE International Journal of Passenger Cars-Electronic and Electrical Systems,2015,8(2015-01-0201)：137-145.

[5]Kidambi N,Harne R L,Fujii Y,et al.Methods in Vehicle Mass and Road Grade Estimation[J].SAE International Journal of Passenger Cars-Mechanical Systems,2014,7(2014-01-0111)：981-991.

[6]Vahidi A, Stefanopoulou A, Peng H. Recur⁃sive Least Squares with Forgetting for Online Estima⁃tion of Vehicle Mass and Road Grade：Theory and Ex⁃periments[J].Vehicle System Dynamics,2005,43(1)：31-55.

[7]李磊,章国胜,宋健,黄全安.基于等效坡度的自动手动变速器换档规律研究[J].公路交通科技,2011(02)：144-148.