题目位置效应的概念及检测*

聂旭刚 陈 平 张缨斌 何引红

(1北京师范大学中国基础教育质量监测协同创新中心; 2北京师范大学教育学部;3北京师范大学数学科学学院, 北京 100875)

1 引言

在1984年至1986年的美国教育进展评估项目(The National Assessment of Educational Progress,NAEP)中, 9岁和17岁受测群体的阅读成绩出现难以置信的异常下降, 这一事件引发一项为期 3年的调查研究, 也即后来被大家所熟知的“1986年NAEP阅读异常研究” (详见Beaton et al., 1988;Beaton & Zwick, 1990)。后续研究表明：导致这一现象的主要原因是NAEP中题册间锚题位置与情境的变化(Zwick, 1991)。这一现象作为测量领域的一个警钟, 提醒研究者们：题目位置和情境的变化会对受测者的作答反应产生不容忽视的影响,尤其是在测验等值设计中。

目前, 测验中因题目位置变化所产生的影响,主要是从题目位置变化如何影响题目参数的角度进行探究。在此背景下, 本文将题目位置效应(Item Position Effect, IPE)定义为：在剔除随机误差的影响之后, 同一个题目在不同测验间因题目位置的变化而导致题目参数的变化。由上述定义并结合以往研究, 可以看出 IPE会对依赖于项目反应理论(Item Response Theory, IRT)参数不变性(parameter invariance)1特征的相关应用、测验公平性以及考生的作答心理等方面造成不利影响。

首先, 在心理与教育测量中, 参数不变性特征是IRT的最大优点(罗照盛, 2012)。IRT正是由于具备这一特性, 才使得它在指导题库建设、计算机化自适应测验(Computerized Adaptive Testing,CAT)中发挥着无法比拟的作用。同时, 参数不变性特征也是测验等值技术得以实现的前提条件;在多种等值设计中, 非等组锚测验设计(Kolen,2006)是最常见的等值数据搜集方法, 这种设计通过一组内嵌在两个平行测验中的锚题来实现两个测验间的等值。而且该设计有一个关键假设：锚题的统计学特性在不同的测验间应该是稳定的,即锚题参数不变性假设。另外, 在矩阵取样(matrix sampling)技术中, 为了实现不同学生之间成绩的比较, 需要在不同题册间设置相同的组块(block)加以链接, 并且组块的位置在各个题册间也是不同的。此时, 链接所使用题目的参数稳定性, 对于矩阵取样设计的有效性具有决定性影响。然而, IPE恰恰是对IRT参数不变性特征的一种违反。所以, 系统研究 IPE的影响, 对于确保IRT应用优势的发挥、降低等值误差、优化矩阵取样技术在大规模测评领域的应用, 都具有十分重要的意义。

其次, 从测验公平性角度来看, 一个公平的题目应该能够给受测者提供平等的机会, 来反映他们已掌握的与测验目的相关的技能和知识(Roever, 2005)。然而在实践中, 题目或者测验水平的公平性很可能会受到题目位置、性别以及种族等因素的影响, 从而导致题目偏差(item bias),并最终对受测者的作答表现产生影响(Zumbo, 1999)。传统的做法是从题目功能差异(Differential Item Functioning, DIF) (即题目参数值在不同子群体间存在变化)的角度来对这种偏差进行分析, 但是也可以从IPE的角度来分析。IPE和DIF一样都会对测验的公平性产生不利影响。但是相比较而言,DIF是从被试特征的差异来探究具有相同目标测量结构的个体在题目参数上的差异, 即考查题目功能所导致的偏差; 这种偏差是由于题目本身功能性特征所决定的, 是由于题目开发过程, 即题目设计所导致的; 而 IPE则是从题目特征的差异来探究题目参数稳定性的影响, 即考查题目情境(即位置)所导致的偏差; 此偏差是由于题目外在情境特征所决定的, 是由于测验设计所导致的。所以, 从偏差产生原因的角度来看, IPE又有别于DIF, 也有国内研究者将其归属为参数漂移(Item Parameter Drift, IPD)产生的原因, 并对 IPD 与DIF进行了系统地区分(叶萌, 辛涛, 2015)。

总的来说, IPE对测验的公平性的不利影响主要体现在依据考生作答反应对其进行分类、选拔等政策性的决策中, 进而会对个人录取、学校资助、地区课程的调整产生较大影响(Hill, 2008;Meyers, Miller, & Way, 2009; Wise, Chia, & Park,1989)。特别是在高利害考试中, 减少这种不利因素, 可以为考生提供相同的机会、维持高水准分类的准确性。

此外, 在认知领域的实验研究中, Weinstein和 Roediger (2010)对测验表现中回顾性偏差(retrospective bias)的研究也表明：题目排列方式的不同, 会使得被试在作答动机、自信心水平以及受测后自我成就评价等方面存在显著的差异。这说明题目位置的变化的确关系到被试的作答心理, 进而会影响被试的作答表现。考试本身就是一种会引起受测者应激反应的事件, 所以在将考试结果作为决策依据使用之前, 任何对被试的作答心理造成差异性影响的因素, 都值得对其进行慎重且全面的考查。

基于这一研究主题的重要性, 本文旨在对IPE进行系统概括和总结, 以期为测量研究者与实践者了解IPE的研究进展以及主要研究思路提供帮助。本文首先对IPE的相关概念(比如参数不变性、题目情境效应、题目顺序效应)进行梳理; 然后系统总结检测 IPE的方法以及相应的模型, 同时从两个角度对 IPE的解释进行概括; 最后, 从四个方面对今后的研究方向进行展望。

2 IPE的相关概念

关于IPE的研究集中于探讨其对IRT参数不变性特征违反所造成的影响, 所以本章节首先对IRT参数不变性特征进行简要介绍。另外, 关于IPE的研究也是随着测量技术的发展以及测量领域问题关注点的变化而不断变化的, 所以结合这一主题的研究进程, 我们也对这期间所涉及的与IPE相似或相关的概念进行区分。

2.1 IRT参数不变性特征

参数不变性特征是IRT在测验领域最实用的特征, 等值、DIF和 IPD等研究主题都是基于参数不变性遭到违反以及由此产生的影响来开展相关研究的。对于参数不变性, 可以从两个角度进行理解：第一, 从同一总体的角度进行理解, 即根据来自同一总体的不同样本所估计得到的参数值不变。比如, 来自同一总体的两批被试样本作答同一批题目, 通过作答反应估计得到的两批题目参数值近似相同; 第二, 从不同总体的角度进行理解, 即根据来自不同总体的样本所估计得到的参数值是存在变化的(Rupp & Zumbo, 2006)。但是它们之间存在某种线性关系, 可以通过等值来进行转换比较。所以总的来说, 参数不变性是指：使用同一总体内不同样本(题目或被试样本)所估计得到的相同被试或相同题目的参数是不变的。

Hambleton和 Swaminathan (1985)明确表达“能力参数的估计独立于特定的选项与题目”是IRT的主要特征, 也是被试间能够进行比较的基础。Meyers等人(2009)认为基于参数不变性特征,研究者可以将 IRT应用到 CAT和预等值(preequating)。可以说, 近年来几乎所有被记录的、对测验实践有益的发展, 都是伴随着 IRT, 或者更确切地说, 是随着参数不变性特征一起出现的(Store, 2013)。但 IPE恰恰是对这一特征的违反(Hill, 2008; Meyers et al., 2009; Wise et al., 1989),所以从这一特征在 IRT应用中的重要地位来看,关于IPE的研究应该引起测量领域相关学者的高度重视。

2.2 IPE概念的演进

IPE是在剔除随机误差的影响之后, 同一个题目在不同测验间因题目位置的变化而导致题目参数的变化。事实上, 这一概念囊括了关于题目位置变化的所有可能情况, 其中包括单个题目的位置变化以及多个题目整体和部分的位置变化(即题目顺序或情境)。常见的两种IPE分别是练习效应(learning effect)和疲劳效应(fatigue effect)(Kingston & Dorans, 1984)。在非速度型测验2在 IPE相关研究领域里涉及的非速度型测验 (unspeeded tests), 都是按照大型测评公司的经验法则进行定义：可以满足100%被试完成75%的题目, 或者不少于80%的被试完成100%的测验题目。中,存在的疲劳效应, 会使得位于测验尾部的题目难度增大; 反之, 练习效应会使得位于测验尾部的题目难度降低。

对以往研究进行梳理发现, 题目情境效应(item context effect)与题目顺序效应(item order effect)本质上都是研究题目位置改变所产生的影响, 所以两者都可以归属于 IPE的概念范畴, 接下来对它们以及彼此的关系进行简要说明。

2.2.1 题目情境效应

Leary和 Dorans (1985)以及 Davey和 Lee(2010, 引自 Store, 2013)等人将题目情境效应定义为：受测者在题目上的作答反应直接或间接地受除“测验想要测量的主要特质或构念”以外一些因素的影响而发生变化。这些影响因素具体包括：题目在测验中的位置(Hill, 2008; Meyers et al.,2009; Whitely & Dawis, 1976; Yen, 1980)、措辞、内容、格式(Kingston & Dorans, 1984; Zwick, 1991)以及该题目周围的其他题目的特殊特征(Davis &Ferdous, 2005; Haladyna, 1992)。由于题目的位置是题目所在情境的一部分, 因而, IPE可以被看作是题目情境效应的特例。

但是, 研究表明：在因情境变化而对被试能力估计产生影响的各种因素中, 题目位置变化的影响是最为显著的(Leary & Dorans, 1985), 因而研究者也集中于探讨位置因素的影响。所以本文认为在心理与教育测量情境下, 关于题目情境效应的研究, 如果主要讨论的是题目情境因素中位置因素对被试作答表现的影响, 题目情境效应就是特指IPE。

2.2.2 题目顺序效应

早期的成就测验中, 经常通过保持测验内容不变而改变题目顺序的方式, 来防止考生抄袭,提高考试安全性。自Mollenkopf (1951)发现题目顺序的变化会对题目难度、区分度有显著影响后,很多研究者都开始探究不同题目排列方式对测验总分的影响(Brenner, 1964; Hanson, 1996; Monk &Stallings, 1970; Moses, Yang, & Wilson, 2007)。题目顺序效应是指一组题目由于题目间顺序的变化所带来的对受测者作答结果的影响。即同一组题目以不同的顺序呈现给同一总体内两组不同的被试作答, 考察两组被试在同一组题目上作答结果的差异。

综合以往的文献描述, 可以将题目顺序和题目位置的研究问题都归为题目排列(item arrangement)方式的研究范畴3题目排列方式即对题目组合设计(如题目顺序、题目位置)的总称, 表示按照某种设计对题目进行编排和安放。进一步细分, 题目排列方式还包含：题目的难易排列、按照课程教学顺序排列等。在本文中, 我们统一将其纳入题目顺序效应的范畴内。因为以往在考查其影响时, 都是以多个题目间顺序改变的形式, 从测验整体层面上来考察其对被试作答的影响。。本质上, 题目顺序效应是 IPE在测验层面的概念, 是同一研究问题在不同研究阶段的名称, 两者可以统称为IPE。两者的关系详见表1。

事实上, 这一研究主题下的研究视角由测验整体层面过渡到单个题目层面的转换, 得益于 70年代末等值技术的应用——由于在等值设计中涉及锚题的使用, 所以在基于 IRT的等值设计中,锚题参数稳定性的相关研究, 使得关于题目排列顺序对考生作答表现影响的探究从多个题目顺序层面转换到单个题目层面。此后, 越来越多的研究者(Debeer & Janssen, 2013; Hartig & Buchholz,2012; Hecht, Weirich, Siegle, & Frey, 2015; Meyers et al., 2009; Qian, 2014; Weirich, Hecht, Penk,Roppelt, & Böhme, 2017), 开始从题目层面上考察单个题目位置的改变对测验题目或者被试作答造成的影响。

总的来说, 以往基于测验总体层面对题目顺序效应的研究, 存在以下的问题：首先, 这些研究仅仅是对某一组特殊的题目进行题目顺序效应的研究, 其结论很难推论到其他测验形式中; 其次,对于题目顺序效应的研究被限定在：不同题册间题目相同只有题目顺序不同的等组设计中; 最后,这些研究仅仅关注题目顺序效应对测验总分的影响, 限制了对这种效应的进一步解释, 从而导致IPE可能会在不同的测验间相互抵消, 进而无法得到检测。

表1 题目位置效应和题目顺序效应的区别和联系

3 题目位置效应的检测和解释

IPE的一般研究思路是：首先, 所考查的测验必须包括两个或多个题册, 部分或所有题目在不同题册中的位置不同。然后, 将不同题册随机分配给不同的被试作答, 获得数据后进行参数估计,再考察题目参数与题目位置的关系。总结以往研究对 IPE建模的程序, 可以将IPE的研究方法分为两步法和一步法。

3.1 两步法

两步法是先对同一题目在不同题册中的参数值分别进行估计, 再通过t检验、方差分析、相关分析或回归分析等统计方法检验相同题目在不同位置时的参数是否有差异, 据此来判断 IPE是否存在以及其对题目参数的影响(e.g., Meyers et al.,2009; Whitely & Dawis, 1976; Yen, 1980)。以往基于两步法的研究主要在以下三个情境下对IPE进行研究：

首先, 在一般的测验情境下。Kingston和Dorans(1982, 1984)、Whitely 和 Dawis (1976)、Yen (1980)通过相关分析考查了题目位置的改变对经典测验理论(Classical Test Theory, CTT)中的通过率, 以及IRT中Rasch难度参数的影响。这些研究都比较一致地发现疲劳效应, 其中 Yen (1980)进一步分析后认为：相对于测验尾部的题目考生会更认真对待位于测验前端的题目, 因而将疲劳效应解释为受测者缺乏耐心。这种对于疲劳效应的理解很具前瞻性, 与近期将 IPE理解为考生努力或者毅力的思路相一致(Debeer, Buchholz, Hartig &Janssen, 2014; Hartig & Buchholz, 2012), 这也进一步佐证了在下一步研究中可以将IPE看作为独立于目标考查维度之外的新维度。

其次, 在测验等值情境下。Davis和 Ferdous(2005)、Eignor和 Cook (1983) 以及Meyers等人(2009)分别考查预试测验(field testing)和正式测验(living testing)中锚题位置变化对其题目参数的影响。研究一致发现当锚题位于预试和正式测验的不同位置时, 锚题的 Rasch难度参数值不同; 而且当预试测验中的题目, 在正式测验中的位置越往测验尾部变化时, 其难度估计值越大。Meyers等人(2009)认为当预试中难度值较小的题目位于正式测验的前端位置、难度值较大的题目位于正式测验的尾部时, 存在显著的与测验等值设计相关的IPE。这说明IPE的确会对以IRT为基础的等值设计的实现有不利影响, 而且这种不利影响对低能力水平的被试更为明显。

最后, 在CAT情境下。Wise等(1989)分析军队计算机化自适应选拔测试(Army's Computerized Adaptive Screening Test, CAST)中的词汇知识和算术推理测验。研究结果表明同一个题目位于测验后半部分时比位于前半部分时的通过率更低、难度估计值更大, 即题目位置的改变会产生疲劳效应; 并且平均通过率达 75%及以上的题册中疲劳效应并不显著, 而平均通过率只有 50%的题册中疲劳效应显著, 即低能力水平的被试更易受疲劳效应的影响。

在两步法的研究方法下, 也有少部分研究考查 IPE对题目区分度的影响, 结果表明在教育测验中相对于对题目区分度参数的影响, IPE对题目难度参数的影响更为明显(Kingston & Dorans, 1982;Yen, 1980)。总体上, 两步法下的研究结果都一致地发现了疲劳效应, 但是针对这一发现研究者们也指出, 必须要首先明晰速度型测验或者测验长度对受测者的作答反应有怎样的影响(Davis &Ferdous, 2005; Yen, 1980)。

两步法的最大优势是数据分析时的简便性,甚至可以在CTT的框架下通过比较同一题目在不同位置时的通过率、题总相关系数等检测测验中是否存在 IPE。但是, 两步法也有一些不足：(1)为了将不同题册中的题目参数链接到同一量尺上, 锚题在不同题册中需要处于相同的位置; (2)没有考虑题目参数的测量误差。具体来说, 两步法将参数估计和IPE检测分开进行：第一步得到题目参数估计值, 第二步将参数估计值和题目位置分别看成因变量和自变量, 并通过方差分析、回归分析等统计方法检测 IPE的存在。这样, 在第二步分析位置对题目参数的影响时假定题目参数估计值不含测量误差, 这样很可能使得分析结果出现偏差; (3)易受样本量的影响。Li, Cohen和 Shen(2012)指出, 当不同题册上的样本量较小时, 使用两步法是不切实际的(尤其是对于 CAT而言),因为样本量太小会导致题目参数估计值存在较大误差, 使得对IPE的检测存在困难。

3.2 一步法

一步法是直接对 IPE进行建模, 即在模型中加入“位置效应参数”, 并将被试在所有题册上的作答数据放在一起进行参数估计。通过比较包含与不包含“位置效应参数”的模型的拟合度, 以及检验“位置效应参数”是否显著不为零, 来判断是否存在 IPE。相对于两步法, 一步法具有以下优势：(1)在模型中加入了量化位置效应的参数, 可以实现题目本身的难度参数和题目位置参数的分离, 进而实现对 IPE更精确的分析; (2)在实现对题目参数和位置参数进行分离的同时, 也可以实现对二者的同时估计; 同时估计考虑了参数的测量误差, 分析结果更为精确。此外, 一步法主要是在解释性项目反应理论(Explanatory Item Response Theory, EIRT) (De Boeck & Wilson, 2004)的框架下构建各类模型以实现对 IPE的检测, 这一框架下的模型不仅可以用于实现对 IPE的检测, 也可以用于下一步的研究中实现对 IPE的解释(比如Debeer & Janssen, 2013)。

已有研究主要是基于将Rasch模型4关于 IPE对于题目区分度参数影响的研究主要集中于人格测验中(Hamilton & Shuminsky, 1990; Steinberg, 1994)。而在成就测验领域中, 这种影响只在极少数研究中得到证实。而本文所讨论的情境主要集中于成就测验领域, 因而所考虑的模型主要基于Rasch模型。进行扩展后的模型对 IPE进行建模, 主要关注位置效应对题目难度参数的影响。公式(1)所示的模型(即模型1。注：以下每个公式都代表一种特定的模型)是对Rasch模型进行logit变换后的形式, 其中logit(Ypik=1)即 ln{ P (Ypik=1)/[1-P (Ypik=1)]},表示发生比的自然对数,Ypik表示被试p在位于k位置的题目i上的作答反应,θp表示被试p的能力水平,βik表示题目i的难度参数5常见的 Rasch模型其难度参数 βi在 IPE的研究情境下可以表示βik, 即题目i在位置k时的难度, 只是在一般情境下,题目的位置不变或者忽略IPE的影响, 于是将βik 简写成βi 。。在模型1中加入“位置效应参数”——f(p,i,k)后得到模型2, 模型2是位置效应模型的统一表达,f(p,i,k)代表位置效应参数是关于题目i、被试p以及位置k的函数。

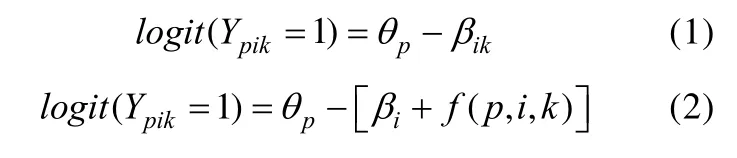
根据研究假设或f(p,i,k)表达形式的不同,可以将一步法范式下的位置效应模型分为三类：第一类模型假设位置效应只与题目位置有关, 而与题目和被试无关, 即f(p,i,k)=f(k); 第二类模型假设位置效应取决于题目位置与题目的交互作用, 即f(p,i,k)=f(i,k); 第三类模型假设位置效应取决于题目位置与被试能力的交互作用, 即f(p,i,k)=f(p,k)。

3.2.1 第一类模型——主效应模型

第一类模型假设题目位置效应独立于题目和被试, 只取决于题目位置。也即同一测验中的所有题目在同一位置上的位置效应值相同。

Kubinger (2008, 2009)和Hohensinn, Kubinger,Reif, Schleich和Khorramdel (2011)等人详述了如何基于线性逻辑斯蒂克模型(Linear Logistic Test Model, LLTM)实现对 IPE的一步法检测。LLTM是将 Rasch模型里的题目难度参数分解为多种基本认知成分的线性组合而得到的(Fischer, 1973),即。其中βik表示 Rasch模型中第i个题目在第k个位置时的难度参数,ηj表示第j个基本认知成分的估计难度,qij表示在一定理论基础上每个认知成分j影响题目i解答的假定概率,即认知成分ηj在题目i上的权重。若将分解为令(r表示基线成分或目标特质)表示当题目i在各测验或题册中位置不变时其基准难度值(或者称在参考位置时的难度值)。而令(k表示位置成分)用来量化 IPE, 表示由于位置改变所构成的难度值, 即题目在位置k时相较于参考位置其难度值的变化量。此时,可看作总题目难度值, 即可得到模型3：

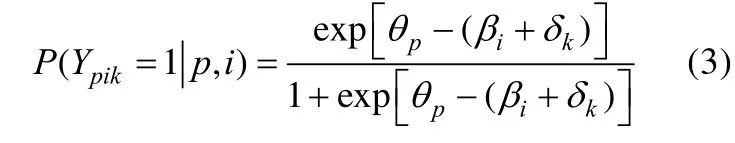
将模型 3进行 logit转换可得到模型 4-1, 此时f(p,i,k)=f(k)=δk。

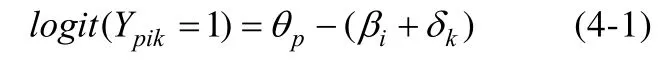
由于模型4-1中并没有添加任何关于IPE的实质结构, 所以对模型进行进一步限定, 将 IPE的值看作是关于题目位置的函数, 即将题目位置当作一个解释性的题目特征加入作答反应函数(De Boeck & Wilson, 2004)。所以在Rasch 模型下,假定难度变化量随题目位置k线性变化, 即可得到模型 4-2, 其中γ表示位置效应的单位改变量,即题目相对于参考位置每变化1个题目位置其难度的变化量。若γ显著不为零, 即表明测验中IPE的存在。进一步来讲, 当γ＞0时, 表示存在疲劳效应;γ＜0时, 则表示存在练习效应。此时f(k)=γ(k−1)。

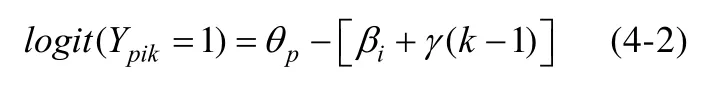
如果难度变化量随位置k非线性变化, 则f(k)可以表示为k的二次函数、指数函数等。以二次函数为例,f(k)=γ1(k–1)+ γ2(k–1)2, 即可得模型4-3 (Kang, 2014)：

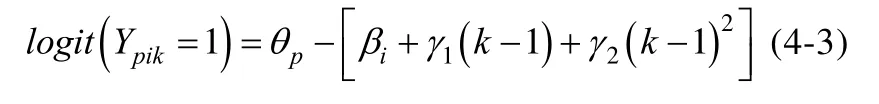
值得注意的是, 在实际问题中, 如果直接在模型中加入二次项系数来模拟难度变化量随位置的非线性变化关系, 则很难对该系数进行解释。

第一类模型假设位置效应的产生独立于题目和被试, 仅受题目位置的影响, 以此来对 IPE进行直接建模。这时得到的位置参数反映了IPE在所有考生、所有题目上的平均效应, 也只能获悉考生能力在测试过程中的一般变化规律, 而无法对不同题目的位置效应情况以及IPE在个体间的差异进行探究。此外, Kubinger (2008, 2009)提出基于 LLTM 来检测 IPE, 实际上是从题目角度出发来对IPE进行研究, 可以看作是在EIRT框架下进行IPE检测以及解释性研究的起点。但是这一方法下的研究存在一个明显的悖论, 即从题目角度模拟IPE, 但从被试角度来解释IPE (如疲劳效应)。

3.2.2 第二类模型——题目位置与题目间的交互作用

第二类模型假设位置效应受题目位置与题目交互作用的影响, 即不同题目在参照位置和k位置之间的难度变化不同。

若模型 4-1和 4-2的位置效应参数与题目i有关, 即f(p,i, k)=f(i,k)=δik以及f(p,i,k)=γi(k–1), 即可得到模型5-1和5-2 (Debeer & Janssen,2013)：

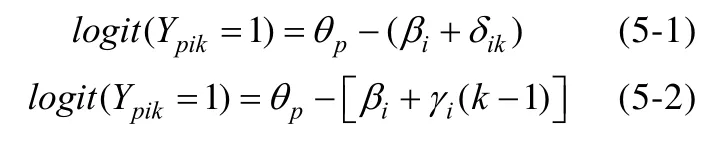
值得注意的是模型5-1中δik与模型4-1中δk的区别, 他们分别表示不同题目i在参照位置和k位置之间的难度变化是不同以及相同的, 即难度的变化受到以及不受到题目内容的影响。此时可以令δik=δk + δik', 其中δk即模型 4-1 中位置的主效应, 也可以理解为平均的位置效应,δik'则是位置k与题目i交互作用的效应值。相应地, 在模型5-2 中令γi=γ + γi', 代入公式后γ(k−1)即模型 4-2中位置的主效应,γi' (k−1)是题目i与位置交互作用的位置效应值。若此时γi显著不为零, 则表明IPE的确存在; 且可以通过比较模型5-2和4-2对同一测验结果的拟合度(如AIC、BIC值)是否存在差异, 来判断是否存在题目位置与题目的交互效应。此外, Kang (2014) 还给出交互效应的二次函数表达式, 即模型5-3:

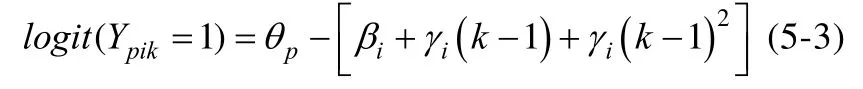
Albano (2013)使用模型5-1和5-2研究GRE词汇和数学测试, 发现位置与题目间存在显著的交互作用, 从而证实 IPE在不同题目间存在显著的差异。另外, Kingston和Dorans (1984)对不同题目类型中 IPE的差异性进行研究, 结果表明：在语文题(verbal items)、数学题(quantitative items)以及分析题(analytical items)三种题型中, 分析题受到题目位置的影响最大, 其次是数学题, 而且都是练习效应。这也说明第二类模型假设位置效应受题目位置与题目的交互作用影响的合理性。

虽然第二类模型在第一类模型的基础上考虑了题目位置与题目交互作用的影响, 使得每个题目都有一个位置参数。但是, 第二类模型也是从题目角度来对 IPE进行解释性研究, 仍存在模拟和解释IPE不一致的问题。

3.2.3 第三类模型——题目位置与被试间的交互作用

第三类模型假设位置效应受题目位置与被试交互作用的影响, 即不同位置的题目其难度的变化受个体差异的影响。

由于不能直接对模型4-1的位置效应参数加上被试p下标, 所以此处我们只讨论基于模型4-2得到的交互作用模型, 即f(p,i,k)=f(p,k)=γp(k–1)时的模型(Hartig & Buchholz, 2012)：

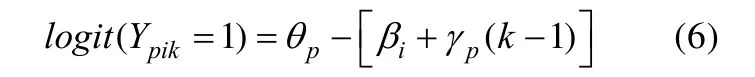
其中γp服从正态分布, 表示对于被试p, 题目相对于参考位置每变化1个题目位置其难度的变化量。相应地, 可以令γp=γ+γp¢, 代入公式 6 后γ(k−1)表示所有被试每答完一道题的平均能力变化量。同样, 若γp显著不为零, 则表明 IPE的确存在; 也可以计算γp与θp的相关系数, 以此来判断 IPE 在个体间的差异。γp¢ (k−1)表示被试p与位置交互作用的位置效应值, 反映被试p每答完一道题其能力在多大程度上(即γp¢绝对值的大小)、往何种方向(即γp¢的正、负号)偏离所有被试的平均能力变化量; 而且γp¢可以看作独立于目标考查维度之外的新维度, 如考生毅力(persistence)或考生努力(examinee effort) (Hartig & Buchholz, 2012;Debeer et al., 2014 )。

IPE的本质是被试在测验过程中能力的变化,不同被试在测验过程中的能力变化必然存在个体差异。因而第三类模型是最符合实际情况的, 即模型中每个被试都有位置参数, 可以得到位置效应对不同被试的影响。此外, Debeer和 Janssen(2013)还对一步法下的三种建模方法进行比较研究, 着重强调了“IPE应被解释为与被试相关的某种特质”, 并指出下一步的研究重点是“对检测出的效应进行进一步的解释”, 即对IPE所代表的新维度进行解释。

总的来说, 基于 IRT框架的一步法在检测IPE时有以下优势：(1)可以将题目位置与设计中的其他题目特征区分开来, 这样就可以得到不同的模型, 比如前面讨论的三类模型; (2)只要两个测验之间存在锚题, 就可将 IPE当作题目本身的属性进行考查, 即模型并不局限于等组设计, 在复杂的非等组设计中同样适用; (3)将IPE对测验总分的影响, 看作其对单个题目分数影响的总和,从而实现在测验分数水平对IPE的考查。比如, 通过测验特征曲线可以概述IPE对测验总分期望值的影响(Debeer & Janssen, 2013); (4)在题目水平模拟 IPE有助于对所发现效应的解释, 比如个体协变量(如性别和测验动机等)可用于解释 IPE所代表的新维度。

除了上述基于 Rasch模型的扩展模型进行建模的方法外, 一步法下的建模思路还可以基于多水平 IRT的视角, 对题目位置的主效应和交互效应进行探究, 即将题目位置作为题目水平的预测变量加入第一水平, 通过定义其第二水平的随机性来确定IPE的类型。

3.2.4 多水平IRT的视角

实质上, 这一研究视角是EIRT框架下研究方法的一种变式。两水平的IRT模型即多水平线性模型中的零模型(刘红云, 骆方, 2008) 如下所示：

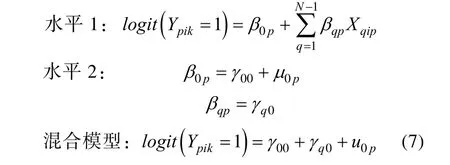
其中p表示被试,i表示题目,k表示位置,N是题目数;Xqip是第p个被试对应的第q个虚拟变量(q=1, 2, …,N-1), 当q=i时,Xqip=1, 否则Xqip=0。u0p服从均值为0的正态分布, 可视为被试p的能力值;γ00可视为第N个题目的容易度(easiness),γq0可视为第q个题目与第N个题目容易度的差值。根据混合模型(mixed models), 可以得到第i个题目的 Rasch 难度值：– γq0– γ00。

Albano (2013)详述了如何根据多水平IRT从主效应和交互效应角度检测 IPE。如果位置效应独立于题目和被试, 在模型 7的水平 1中加入位置效应参数作为预测变量, 即可得主效应模型8：

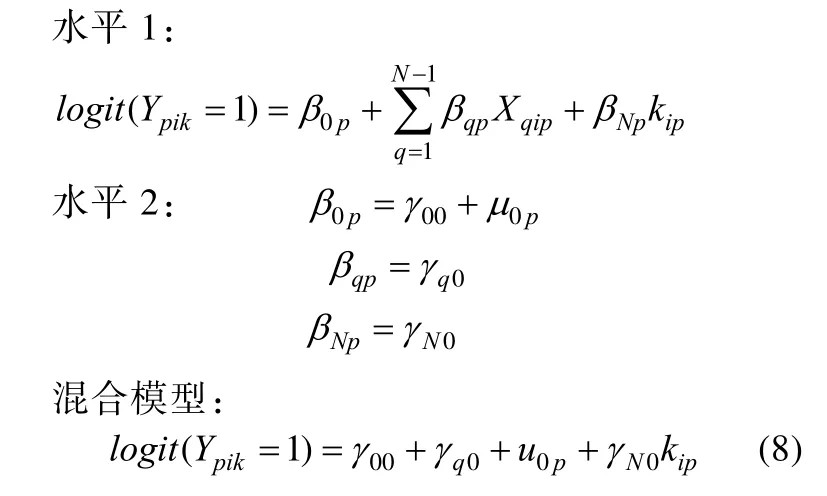
其中βNp是位置的主效应,kip(kip=1, 2,…,N)是被试p作答的题目i(也即q=i)所处的位置,γN0为位置的固定效应, 表示所有位置间成绩得分的总平均变化。模型8与模型4-2相对应。另外, 如果位置与题目有交互作用, 则在模型 8的水平 1中再加入(N–1)个题目与位置的交互作用参数, 即可得到交互效应模型9：

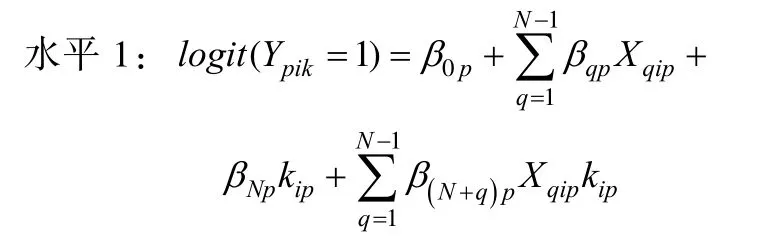
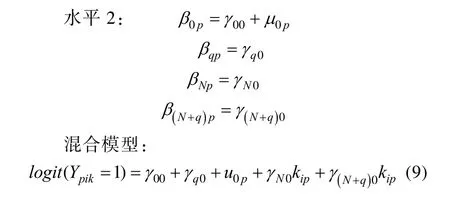
其中β(N+q)p表示题目与位置交互作用下的位置效应。模型9与模型5-2相对应。类似的, 如果位置与被试有交互作用, 则在模型 8中加入位置与被试交互作用参数, 得到交互效应模型10。

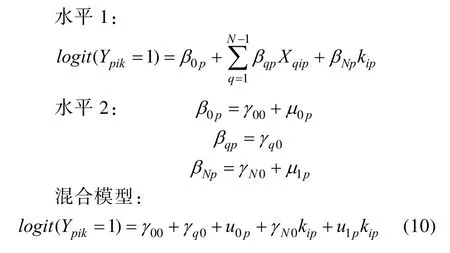
此时位置效应βNp包括两部分：固定效应——位置的主效应γN0和随机效应——位置与被试的交互作用u1p, 而且u1p服从均值为零的正态分布。模型10与模型6相对应。Debeer等人(2014)从多水平 IRT的视角出发, 在模型中加入组水平变量来探究IPE在不同学校、国家间的差异。

目前关于 IPE的检测模型, 都可以看作是基于EIRT的框架下探讨题目位置的主效应、交互效应模型。表2对检测IPE的一步法模型进行了详细对比。

表2 检测IPE一步法的汇总

3.2.5 参数估计

以上模型都可归为广义线性混合模型(generalized linear mixed model), 可用一般的统计软件实现模型的参数估计, 比如R软件lme4包中的lmer函数(Debeer & Janssen, 2013)以及HLM7(Hartig & Buchholz, 2012; Albano, 2013)。如果在以上模型中加入区分度, 这些模型则属于非线性混合模型(De Boeck & Wilson, 2004), 此时可使用SAS软件中的 NLMIXED程序包估计模型参数(Debeer & Janssen, 2013)。

3.3 对IPE的解释

以往的研究主要是从题目和被试两个角度对IPE进行解释。第一, 从题目角度对 IPE 进行解释时会将题目难度参数看成多种认知成分的线性组合(Kubinger, 2008, 2009)。基于这一角度的研究主要从测验的整体层面或者单个题目层面探究题目位置改变对被试作答结果的影响, 并且根据被试作答结果的变化趋势, 将 IPE概括为练习效应或疲劳效应。但是这一角度的研究思路会产生一个悖论, 即模拟时从题目角度出发, 但解释时是从被试角度来解释, 比如疲劳效应。这一悖论会使得研究者不能清楚理解IPE或其所指代的真正含义。

第二, 从被试角度对IPE进行解释, 即将IPE看作独立于目标考查维度之外的新维度。Hartig和Buchholz (2012)提出的被试和题目的交互效应模型, 首次将 IPE看作独立于能力维度之外的新维度, 并且标记为毅力。另外, Debeer等人(2014)在Hartig和Buchholz (2012)的研究基础上, 将位置效应维度理解为考生努力, 并且使用多水平IRT对 IPE进行校际、国家之间的比较。虽然这些研究将 IPE看成新维度, 但是对新维度的定义缺乏相应的理论支持; 而且研究者往往基于个人经验和实际研究中的方便, 将 IPE所代表的新维度定义为考生毅力或考生努力, 仍没有研究加入与个体有关的预测变量来对 IPE进行解释。同时,他们也指出这一新维度还可以从动机、测验过程中的学习能力等特质因素来理解(Hartig & Buchholz,2012)。所以, 目前这一新维度表示什么特质尚未有定论。

4 讨论与展望

IRT依赖其参数不变性特征, 在测验等值、CAT、题库建设以及大规模测评中的抽样设计等方面做出突出的贡献, 大大丰富了测验理论及其在实践中的应用。在这些应用过程中, 也需要不断检验参数不变性特征是否能够得到满足。而IPE是对 IRT参数不变性的直接违反, 因而会对基于该特征的相关应用产生直接的影响。本文首先对IRT参数不变性特征的具体含义进行了介绍, 然后对与 IPE相关或相似的概念进行区分, 希望能够帮助研究者今后更全面地理解IPE的含义、了解这一主题的发展过程。本文在第三部分重点总结了检测 IPE的两种主要方法——两步法和一步法, 特别对当前主要使用的一步法的三类建模思路进行详细总结。从解释性 IRT的角度来看, 这三类建模思路实质上也对应着不同的IPE解释角度, 即从题目角度或从被试角度对IPE进行解释。综合以往研究的结论和局限性, IPE今后的研究方向包括以下四个方面：

4.1 探究和开发检测IPE的新模型、新方法

如上文所总结的, 基于 IRT框架的一步法主要包括三类模型, 其中第一类模型所能提供的信息后两类模型都能提供。使用第二类模型得到的结果有助于剔除那些受位置效应影响大的题目,从而提高测试的信效度。使用第三类模型得到的结果则有助于明晰位置效应对不同被试的作用;这也是最符合实际的一类模型, 因为 IPE的本质是被试在测验过程中的能力波动, 不同被试在测验过程中的能力波动理应不同。

一步法下的这三类模型虽然考虑了题目参数的测量误差, 相比两步法更精确, 但是仍存在以下不足：(1)将IPE限定在“个体对于题目的作答反应是独立的”, 即题目间的作答结果是相互独立、互不影响的。但是在实际情形中该限定条件容易被违反, 比如在练习效应中, 成功的作答相对于错误的作答会产生更大的练习效应。所以, 需要使用诸如动态(dynamic) IRT模型等特殊的模型处理这类情境; (2)不能考查由一个题目先于另一个题目(比如一个难题位于一个简单题目的前面)所产生的效应, 这种序列效应(sequencing effects)也是关于题目位置的函数, 但是这种效应涉及的是某题目的子集(比如一对题目), 然而目前基于IRT框架的一步法仅仅关注一个题册内的某个题目;(3)现有研究主要集中于侦查和模拟 IPE, 没有引入与个体有关的变量对IPE进行解释性研究。

鉴于以往研究已经证明IPE可以看作是独立于被试能力维度之外的新维度(Debeer & Janssen,2013; Hartig & Buchholz, 2012), 所以在今后的研究中可以使用多维模型来进一步模拟和检测 IPE;还可以借鉴追踪数据的分析方法, 将每个被试在每个题目位置的测量, 看作是追踪研究中每个被试在每个时间点的测量, 并借助相关的纵向 IRT模型(Embretson, 1991; Paek, Baek, & Wilson, 2012;Roberts & Ma, 2006; Von Davier, Xu, & Carstensen,2011)进行分析。值得注意的是, 针对一步法的建模范式, 除了 IRT的视角也可以从验证性因子分析的视角探究 IPE, 感兴趣的读者可以参考 Schweizer,Schreiner和 Gold (2009)以及 Schweizer, Troche和Rammsayer (2011)等。

4.2 对检测到的IPE进行进一步的解释

就像DIF的研究进程一样(Zumbo, 2007), 在检测 IPE并探究其影响之后, 下一步需要对所发现效应进行解释(Debeer & Janssen, 2013)。研究者可以根据EIRT中的个体解释性模型(person explanatory models) (De Boeck & Wilson, 2004), 对所发现的结果进行进一步的解释。例如, 已有研究已经证实, 在低利害的测评中受测者会在测验动机上存在显著差异, 因此可以考虑将对被试动机水平的自我报告测量(比如Wise & DeMars, 2005), 或者反应时(比如Wise & Kong, 2005)加入到IRT模型中, 作为额外的被试预测变量对 IPE进行进一步解释。另外, Borgonovi和Biecek (2016)认为目前在低利害的国际测评中, 所测量的实际是个体技能(skill)与意志(will)的组合, 其研究结果表明：考试毅力可以看作是学生在测验过程中运用自我控制能力的函数, 而且这种能力依赖于考试动机。因而他们认为, 考试毅力也应该是低利害测评中所测量的维度之一。因此, 下一步的解释性研究可以从考试毅力的角度出发, 在模型中引入与个体有关的变量, 探究 IPE在个体间的差异或者个体变量对IPE的预测作用, 进而实现对 IPE的进一步解释。

4.3 在特定情境下考察IPE

鉴于 IPE影响的广泛性, 以往研究结合特定的研究情境对IPE进行多视角的探究。这些研究包括：

首先, Talento-Miller, Rudner, Han和 Guo(2012，引自 Store，2013)在 CAT中研究 IPE, 结果表明位置的变化会对被试的作答表现产生影响(比如疲劳效应)。另外, 因题目位置变化而导致的参数差异值的大小, 会因具有不同反应时的题型而变化。

再者, 在等值设计中, Store (2013)在其博士论文中对该领域内有关IPE的研究进行了详细论述, 并进一步探究不同的等值设计是否会加剧或减弱 IPE。大量的研究表明：锚题位置的变化会对等值结果产生显著的影响(Whitely & Dawis,1976; Yen, 1980; Davis & Ferdous, 2005; He, Gao,& Ruan, 2009)。在等值设计中, 锚题在各个题册中都不应该存在 DIF, 而且在各个题册中也应该被安排在相同的位置上(Cook & Petersen, 1987)。甚至有研究者认为, 锚题题目选项的位置都不应该被改变(Cizek, 1994)。IPE的存在会对等值技术的有效性构成许多挑战。Weirich, Hecht和Böhme (2014)还认为在进行任何基于锚题的链接设计之前, 都必须首先确定IPE在所有的样本上是一致的。

正如Kolen和Brennan (2004)所指出的：测验的开发和等值是密不可分的。我们不应该再继续忽略等值过程中因题目设计或测验开发所带来的问题, 而应该尽量去克服这些设计所带来的问题。以往的研究也表明：不论题目的位置产生怎样的变化(向前、向后或者向中间位置移动)都会带来一定的影响; 从这一角度看, 建议研究者今后可以考虑更深层次的等值方法, 比如可以考虑用相同的因子载荷来代替锚题等。

另外, 在表现性评价(performance assessments)中, 比如建构反应性试题、短文以及口头表述等,相较于传统的选择题能更好地测量出学生在真实世界中的复杂成就和情意表现, 因而逐渐受到各领域的青睐(赵德成, 2013)。但是, 对其进行等值设计或者对不同时间段的测评结果进行比较时,则存在很大的挑战, 这其中就包含因题目顺序变化所带来的偏差问题(Muraki, Hombo & Lee, 2000)。

因此, 下一步研究者除了可以继续在这些研究主题下进一步深化之前的研究, 也可以在其他研究情境下探讨 IPE的影响。比如, 由于题组(testlet)的使用越来越普遍, 针对题组的等值和DIF都得到相应的研究。所以相应地, 也可以对题组位置变化的影响进行探究。

4.4 探究平衡或消除IPE的方法

无论在基础研究领域还是实践应用领域, IPE的研究都具有很大的必要性。如果忽略这一效应,将会对研究本身和实际工作产生一系列的不利影响(Wu, 2010; Meyers, Murphy, Goodman, & Turhan,2012; Debeer & Janssen, 2013)。所以, 探究平衡或消除IPE的方法也应该引起研究者的关注。

首先, 测验设计方面的研究表明：可以通过题目位置平衡设计的方法降低由IPE导致的参数变化。其基本设计是：令题目在每个位置上的呈现次数完全相同, 此时由于题目位置变化所产生的效应量对于所有题目是相同的, 从而消除 IPE带来的不利影响(Hecht et al., 2015; Weirich et al.,2014)。再者, 也有研究结果表明：整体移动包含多个题目的阅读理解题目(即题组), IPE对题目参数的影响不明显(Haladyna, 1992)。对此有研究者分析认为, 这主要是由于题组的移动是按照一组题目整体移动的, 所以这其中的单个题目就其周围的题目而言其位置是相对不变的, 所以位置变化的影响不明显(Store, 2013), 但这一观点有待进一步确定。

致谢：感谢美国明尼苏达大学王纯(Chun Wang)博士和加拿大阿尔伯塔大学崔迎(Ying Cui)博士对本文的英文摘要进行修改和润色, 感谢北京师范大学中国基础教育质量监测协同创新中心的高一珠同学和陈冠宇同学对文章行文结构的建议。

刘红云, 骆方.(2008).多水平项目反应理论模型在测验发展中的应用.心理学报, 40(1), 92–100.

罗照盛.(2012).项目反应理论基础.北京: 北京师范大学出版社.

叶萌, 辛涛.(2015).题目参数漂移: 概念厘定及相关研究.心理科学进展, 23(10), 1859–1868.

赵德成.(2013).表现性评价: 历史、实践及未来.课程.教材.教法,(2), 97–103.

Albano, A.D.(2013).Multilevel modeling of item position effects.Journal of Educational Measurement, 50(4),408–426.

Beaton, A.E., Ferris, J.J., Johnson, E.G., Johnson, J.R.,Mislevy, R.J., & Zwick, R.(1988).The NAEP 1985–86 reading anomaly: A technical report.Princeton, NJ:Educational Testing Service.

Beaton, A.E., & Zwick, R.(1990).The effect of changes in the national assessment: Disentangling the NAEP 1985–86 reading anomaly.Princeton, NJ: Educational Testing Service.

Borgonovi, F., & Biecek, P.(2016).An international comparison of students' ability to endure fatigue and maintain motivation during a low-stakes test.Learning and Individual Differences, 49, 128–137.

Brenner, M.H.(1964).Test difficulty, reliability, and discrimination as functions of item difficulty order.Journal of Applied Psychology, 48(2), 98–100.

Cizek, G.J.(1994).The effect of altering the position of options in a multiple-choice examination.Educational and Psychological Measurement, 54(1), 8–20.

Cook, L.L., & Petersen, N.S.(1987).Problems related to the use of conventional and item response theory equating methods in less than optimal circumstances.Applied Psychological Measurement, 11(3), 225–244.

Davis, J., & Ferdous, A.(2005).Using item difficulty and item position to measure test fatigue.Paper presented at the annual meeting of the American Educational Research Association, Montreal, Quebec.

Debeer, D., Buchholz, J., Hartig, J., & Janssen, R.(2014).Student, school, and country differences in sustained test-taking effort in the 2009 PISA reading assessment.Journal of Educational and Behavioral Statistics, 39(6),502–523.

Debeer, D., & Janssen, R.(2013).Modeling item-position effects within an IRT framework.Journal of Educational Measurement, 50(2), 164–185.

De Boeck, P., & Wilson, M.(2004).Explanatory item response models: A generalized linear and nonlinear approach.New York, NY: Springer.

Eignor, D.R., & Cook, L.L.(1983).An investigation of the feasibility of using item response theory in the pre-equating of aptitude tests.Paper presented at the annual meeting of the American Educational Research Association, Montreal, Quebec.

Embretson, S.E.(1991).A multidimensional latent trait model for measuring learning and change.Psychometrika,56(3), 495–515.

Fischer, G.H.(1973).The linear logistic test model as an instrument in educational research.Acta Psychologica,37(6), 359–374.

Haladyna, T.M.(1992).Context-dependent item sets.Educational Measurement: Issues and Practice, 11(1),21–25.

Hambleton, R.K., & Swaminathan, H.(1985).Item response theory: Principles and Applications(Vol.7).Boston:Kluwer Academic Pub.

Hamilton, J.C., & Shuminsky, T.R.(1990).Self-awareness mediates the relationship between serial position and item reliability.Journal of Personality & Social Psychology,59(6), 1301–1307.

Hartig, J., & Buchholz, J.(2012).A multilevel item response model for item position effects and individual persistence.Psychological Test and Assessment Modeling, 54(4), 418–431.

He, W., Gao, R., & Ruan, C.Y.(2009).Does pre-equating work? An investigation into pre-equated testlet-based college placement exam using post administration data.Paper presented at the annual meeting of the National Council on Measurement in Education, San Diego, California.

Hecht, M., Weirich, S., Siegle, T., & Frey, A.(2015).Effects of design properties on parameter estimation in large-scale assessments.Educational and Psychological Measurement,75(6), 1021–1044.

Hill, R.(2008).Using P-value statistics to determine the believability of equating results.Paper presented at the National Conference on student assessment, Orlando,Florida.

Hohensinn, C., Kubinger, K.D., Reif, M., Schleicher, E., &Khorramdel, L.(2011).Analysing item position effects due to test booklet design within large-scale assessment.Educational Research and Evaluation, 17(6), 497–509.

Hanson, B.A.(1996).Testing for differences in test score distributions using loglinear models.Applied Measurement in Education, 9(4), 305–321.

Kang, C.(2014).Linear and nonlinear modeling of item position effects(Unpublished master’s thesis).University of Nebraska-Lincoln.

Kingston, N.M., & Dorans, N.J.(1982).The effect of the position of an item within a test on item responding behavior: An analysis based on item response theory.Research Report RR-82–22.Princeton, NJ: Educational Testing Service.

Kingston, N.M., & Dorans, N.J.(1984).Item location effects and their implications for IRT equating and adaptive testing.Applied Psychological Measurement,8(2), 147–154.

Kolen, M.J.(2006).The kernel method of test equating.Psychometrika, 71(1), 211–214.

Kolen, M.J., & Brennan, R.L.(2004).Test equating, scaling,and linking: Methods and practices.New York: Springer.

Kubinger, K.D.(2008).On the revival of the Rasch model-based LLTM: From constructing tests using item generating rules to measuring item administration effects.Psychology Science Quarterly, 50(3), 311–327.

Kubinger, K.D.(2009).Applications of the linear logistic test model in psychometric research.Educational and Psychological Measurement, 69(2), 232–244.

Leary, L.F., & Dorans, N.J.(1985).Implications for altering the context in which test items appear: A historical perspective on an immediate concern.Review of Educational Research, 55(3), 387–413.

Li, F.M., Cohen, A., & Shen, L.J.(2012).Investigating the effect of item position in computer–based tests.Journal of Educational Measurement, 49(4), 362–379.

Meyers, J.L., Miller, G.E., & Way, W.D.(2009).Item position and item difficulty change in an IRT-Based common item equating design.Applied Measurement in Education, 22(1), 38–60.

Meyers, J.L., Murphy, S., Goodman, J., & Turhan, A.(2012).The impact of item position change on item parameters and common equating results under the 3PL model.Paper presented at the annual meetings of the National Council on Measurement in Education,Vancouver, British Columbia.

Mollenkopf, W.G.(1951).Prediction of second-year and third-year grade-point averages at the U.S.naval postgraduate school.ETS Research Bulletin, 1951(2), i–36.

Monk, J.J., & Stallings, W.M.(1970).Effects of item order on test scores.Journal of Educational Research, 63(10),463–465.

Moses, T., Yang, W.L., & Wilson, C.(2007).Using kernel equating to assess item order effects on test scores.Journal of Educational Measurement, 44(2), 157–178.

Muraki, E., Hombo, C.M., & Lee, Y.W.(2000).Equating and linking of performance assessments.Applied Psychological Measurement, 24(4), 325–337.

Paek, I., Baek, S.G., & Wilson, M.(2012).An IRT modeling of change over time for repeated measures item response data using a random weights linear logistic test model approach.Asia Pacific Education Review, 13(3), 487–494.

Qian, J.H.(2014).An investigation of position effects in large-scale writing assessments.Applied Psychological Measurement, 38(7), 518–534.

Roberts, J.S., & Ma, Q.(2006).IRT models for the assessment of change across repeated measurements.In R.W.Lissitz (Ed.),Longitudinal and value added models of student performance(pp.100–127).Maple Grove, MN:JAM Press.

Roever, C.(2005).“That’s not fair!” Fairness, bias and differential item functioning inlanguage testing.Retrieved February 10, 2012, from http://www2.hawaii.edu/~roever/brownbag.pdf

Rupp, A.A., & Zumbo, B.D.(2006).Understanding parameter invariance in unidimensional IRT models.Educational and Psychological Measurement, 66(1), 63–84.

Schweizer, K., Schreiner, M., & Gold, A.(2009).The confirmatory investigation of APM items with loadings as a function of the position and easiness of items: A two–dimensional model of APM.Psychology Science Quarterly, 51(1), 47–64.

Schweizer, K., Troche, S.J., & Rammsayer, T.H.(2011).On the special relationship between fluid and general intelligence: New evidence obtained by considering the position effect.Personality and Individual Differences,50(8), 1249–1254.

Steinberg, L.(1994).Context and serial-order effects in personality measurement: Limits on the generality of measuring changes the measure.Journal of Personality &Social Psychology, 66(2), 341–349.

Store, D.(2013).Item parameter changes and equating: An examination of the effects of lack of item parameter invariance on equating and score accuracy for different proficiency levels(Unpublished doctorial dissertations).The University of North Carolina at Greensboro.

Von Davier, M., Xu, X.L., & Carstensen, C.H.(2011).Measuring growth in a longitudinal large-scale assessment with a general latent variable model.Psychometrika, 76(2),318–336.

Weinstein, Y., & Roediger, H.L.(2010).Retrospective bias in test performance: Providing easy items at the beginning of a test makes students believe they did better on it.Memory & Cognition, 38(3), 366–376.

Weirich, S., Hecht, M., & Böhme, K.(2014).Modeling item position effects using generalized linear mixed models.Applied Psychological Measurement, 38(7), 535–548.

Weirich, S., Hecht, M., Penk, C., Roppelt, A., & Böhme, K.(2017).Item position effects are moderated by changes in test-taking effort.Applied Psychological Measurement,41(2), 115–129.

Whitely, S.E., & Dawis, R.V.(1976).The influence of test context on item difficulty.Educational and Psychological Measurement, 36(2), 329–337.

Wise, L., Chia, W., & Park, R.(1989).Item position effects for test of word knowledge and arithmetic reasoning.Paper presented at the annual meeting of the American Educational Research Association, San Francisco, California.

Wise, S.L., & DeMars, C.E.(2005).Low examinee effort in low-stakes assessment: Problems and potential solutions.Educational Assessment, 10(1), 1–17.

Wise, S.L., & Kong, X.J.(2005).Response time effort: A new measure of examinee motivation in computer–based tests.Applied Measurement in Education, 18(2), 163–183.

Wu, M.(2010).Measurement, sampling, and equating errors in large-scale assessments.Educational Measurement:Issues and Practice, 29(4), 15–27.

Yen, W.M.(1980).The extent, causes and importance of context effects on item parameters for two latent trait models.Journal of Educational Measurement, 17(4), 297–311.

Zumbo, B.D.(1999).A handbook on the theory and methods of differential item functioning (DIF): Logistic regression modeling as a unitary framework for binary and Likerttype (ordinal) item scores. Ottawa ON: Directorate of Human Resources Research and Evaluation, Department of National Defense.

Zumbo, B.D.(2007).Three generations of DIF analyses:Considering where it has been, where it is now, and where it is going.Language Assessment Quarterly, 4(2), 223–233.

Zwick, R.(1991).Effects of item order and context on estimation of NAEP reading proficiency.Educational Measurement: Issues and Practice, 10(3), 10–16.