全信息项目双因子分析：模型、参数估计及其应用*

毛秀珍 夏梦连 辛 涛

(1四川师范大学教育科学学院; 2四川师范大学教师教育与心理学院, 成都 610068)

(3北京师范大学协同创新中心, 北京 100875)

1 引言

随着心理测量理论和技术的发展, 科学研究与实践工作已越来越离不开各类测验(量表)了。测验(量表)的结构作为解释测验分数的基础, 一直是测验(量表)开发的重要内容之一。事实上, 大部分测验都是为了测量单一特质而从多个相互关联的维度或层面进行抽样来设计项目。例如, 在建构生活质量量表时, 研究者一般会从工作满意、家庭经济状况、健康和社会生活等多个方面来抽样和设计项目。这种两阶段抽样程序, 往往导致领域内部相关高于领域之间的相关, 项目反应在测验考察的主要维度上不满足条件独立性, 从而使测验结构变得更加复杂。一般地, 测验或量表的测量结构可以划分为以下五类：单维模型(unidimensional model)、多个单维模型(multiunidimensional model)、相关特质多维模型(correlated traits multidimensional model)、二阶因子模型(secondorder factor model)和双因子模型(bifactor model)。

其中, 单维模型(见图 1(a))的限制条件最严格, 它要求所有项目测量同一个特质, 该特质解释所有项目反应的协方差。图 1(b)和(c)所示的两类项目间多维模型(between-item multidimensional model)要求每个项目只在一个因子上有负载。它们虽然包含多个因子, 但是可形成多个子量表,并可用单维项目反应理论(Item Response Theory,IRT)模型去拟合各个子量表。图 1(b)假设因子之间相互独立, 结构简单, 又称为多个单维 IRT模型。但是它很少用于检测实证数据的潜特质结构。而图1(c)允许因子相关, 能同时估计多个潜在特质, 与多个单维模型相比提高了测验效率。但相关特质模型通常存在高阶特质, 混淆了一阶因子和高阶因子, 当测验(项目)拟合检验很差时,不能指出因子结构的错误(Reise, 2012)。图1 (d)所示的二阶因子模型包括6个观察变量、两个一阶因子和一个二阶因子。如图所示, 二阶因子与观察变量不直接相关, 它对观察变量的效应通过一阶因子的中介起作用, 其效应量与一阶因子在二阶因子上的负载成比例(Seo & Weiss, 2015)。二阶因子反映一阶因子之间的相关, 根据二阶因子在一阶因子上的负载可以反映其能够解释一阶因子的程度。因而, 二阶因子在概念上是一个抽象结构, 根据研究者对一阶因子的理解从而对二阶因子的解释可能不同。图1 (e)所示的双因子模型中, 一般因子(general factor, G)和特定领域因子或称为组因子(specific domain factor or group factor, S)与观察变量直接相关, 相互独立地解释观察变量的变异。其中, 一般因子解释所有项目间的相关, 多个“组因子”独立于一般因子, 解释项目组中去掉被一般因子所解释的那部分变异外的共同变异。组因子可能代表子量表或项目组测量的特殊特质, 也可能是无关因子(例如项目在表达上存在正相关或负相关, 或者观察变量受到共同提示的影响)。

除了图 1所示的差异外, 这几个测量模型同时还具有密切联系。双因子模型中当一般因子的负载显著大于组因子的负载时, 一般因子可以解释为本质上是单维模型所测量的潜在特质。Yung,Thissen和 McLeod (1999)运用推广的 Schmidleiman转换方法(Schmid & Leiman, 1957), 证明在不满足有关比例的约束条件时二阶因子模型潜套于双因子模型, 当加上关于比例的约束条件时双因子模型和二阶因子模型等价。这里比例的约束条件包括(1)双因子模型中一般因子在项目上的负载等于二阶因子模型中二阶因子在对应一阶因子的负载与该一阶因子在项目上负载的乘积; 和(2)双因子模型中, 一般因子和对应组因子在每个项目上的负载的比例相等(Chen, West, & Sousa,2006)。一般地, 当维度之间不相关或相关较弱(相关系数在 0.1以下), 建议采用多个单维模型; 当维度之间存在中、低等相关时(相关介于0.1到0.4),项目在一般因子的负载小于组因子的负载, 建议使用相关特质 MIRT模型; 当维度间存在中、高等相关时(相关系数在0.4以上), 建议采用双因子模型(Reise, Morizot, & Hays, 2007)。

与二阶因子模型、相关特质模型和单维模型相比, 双因子模型具有很多优势。首先, 双因子模型很容易解释一般因子对项目的影响, 通过检验一般因子与组因子对项目的直接影响, 可以比较不同因子的重要性(Canivez, 2016)。然而, 二阶因子模型中高阶因子代表一阶因子的变异, 不能直接检验高阶因子和项目之间关系的强度。其次,双因子模型中还可以检验去掉一般因子的影响之后, 组因子的测量结构在两个或多个被试组之间是否等价。特别地, 当给定足够水平的测量不变性时, 它能比较不同被试组在一般因子和组因子上的差异。然而, 二阶因子模型中只能检验二阶因子的测量不变性和比较不同被试组在二阶因子上的差异。再次, 与多个单维模型相比, 双因子模型可以提供更准确的项目参数、特质估计和测验信度(DeMars, 2006)。此外, 双因子模型还可以检验单维模型在拟合多维数据时的失真情况。

Holzinger和 Swineford (1937)提出的双因子模型在近 20年得到了重新认识并作为一种多维特质模型广泛应用于医学、心理学和教育学领域。下面首先介绍了全信息项目双因子分析的概念,然后描述全信息项目双因子分析的基础模型, 并介绍参数估计中体现的维度缩减思想, 接着例举全信息项目双因子方法在分析测验结构、分数解释和计算机化自适应测验(Computerized Adaptive Testing, CAT)中的应用, 最后对全信息项目双因子分析的理论研究和实践应用提出一些思考和建议。

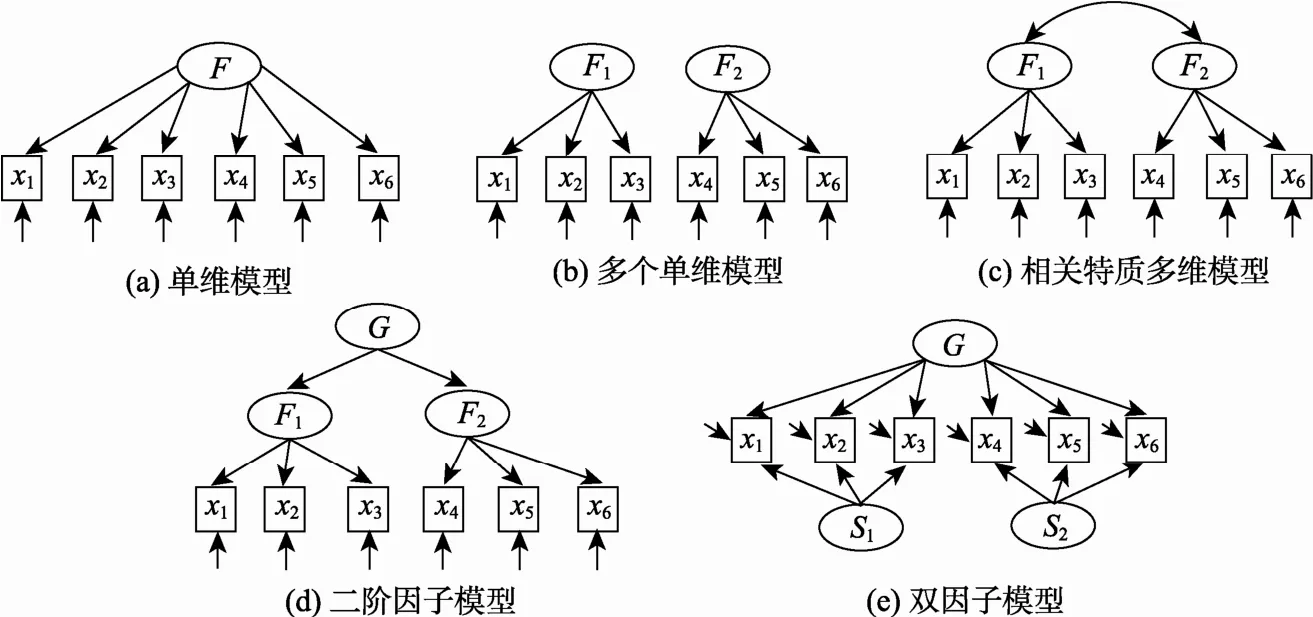
图1 五种测验（量表）结构

2 全信息项目双因子分析的概念与特征

双因子模型最初定义在测验水平上(Holzinger& Swineford, 1937), 表示由多个高相关领域共同测量一个一般特质的因素结构模型并用于分析具有连续分布的测验分数。如今, 双因子模型主要应用到项目水平, 并通常用图 1(e)所示的路径图来表示其测量结构。具体而言, 双因子模型要求每个观察变量测量一般因子和一个组因子, 多个观察变量共同测量一个组因子。换言之, 每个变量只在一般因子和一个组因子的负载不等于 0,图1(e)中因子负载矩阵y表示为,

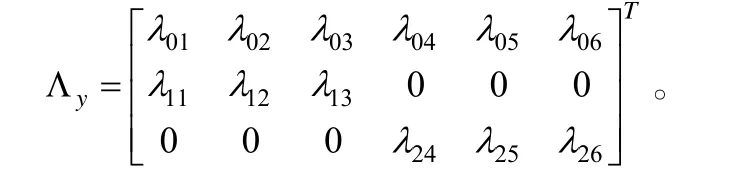
表示一般因子在第j个项目的负载;和分别表示第一个和第二个组因子在第j个项目上的负载; T表示矩阵转置。

全信息项目双因子分析是以双因子模型为基础, 应用项目反应理论分析作答反应, 获得有关项目、测验和被试特征的数据分析方法。它具有如下特征, 第一, 全信息项目双因子分析中双因子模型定义在项目水平上。第二, 全信息项目双因子分析运用双因子项目反应理论模型分析被试在项目上的原始作答数据。而传统线性双因子分析方法则对项目反应数据(或子量表总分)的相关或协方差矩阵进行分析。基于原始数据来源于项目水平, 没有经过统计处理包含了被试的全部信息, 因而称其为“全信息项目双因子分析”。全信息项目双因子分析中为保证模型识别问题并且可以直接使用“维度缩减” (dimension reduction)方法,通常假设一般因子与组因子相互独立, 组因子之间相互独立。“维度缩减”方法是全信息项目双因子分析的重要特征。因为无论测验考察多少个能力维度, 它都使双因子项目反应模型中项目参数边际似然函数的积分化简为多个二维迭代积分。事实上, 若仅针对模型识别问题, 双因子模型假设可以放松为在一般因子条件下特定领域因子之间满足条件独立性(Rijmen, 2009)。

3 全信息项目双因子分析的基础模型和参数估计

全信息项目双因子分析的模型基础是双因子项目反应理论模型。根据双因子模型对每个项目只测量一般因子和一个组因子的假设对多维项目反应理论(multidimensional item response theory,MIRT)模型进行改写可以获得双因子项目反应理论模型。目前, 较为熟知的双因子项目反应模型包括适用于二级评分项目的正态肩形模型和logistic模型、适用于多级评分项目的等级反应模型、分部评分模型和称名反应模型。

3.1 双因子项目反应理论模型

3.1.1 二级评分双因子项目反应模型

Gibbons和Hedeker (1992)首次将双因子因素结构引入IRT, 提出双因子正态肩形模型。Gibbons等人 (2007) 进一步将双因子正态肩形模型推广到双因子等级反应模型。他们利用边际极大似然估计方法推导项目参数估计值时发现, 双因子模型假设能力相互独立, 极大地简化了似然方程的计算。但是他们的推导依赖于双变量正态积分,从而将测量模型限制为正态肩形模型。Rijmen(2009) 运用图理论证明双因子模型假设在更一般IRT模型下同样能简化边际似然函数的计算。Cai, Yang和Hansen (2011)则进一步描述了双因子logistic模型、多级评分项目双因子模型以及参数估计方法。其中, 双因子三参数logistic模型中被试i正确做答项目j的概率表示为：

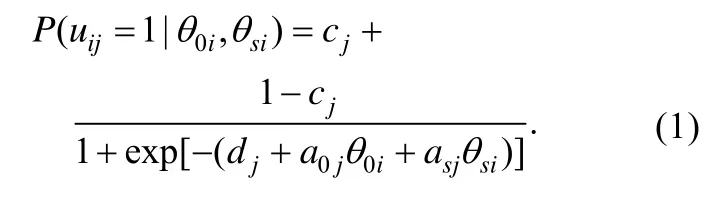
这里,a0j和asj分别表示项目j在一般因子和组因子上的斜率参数, 代表了项目反应与因子之间联系的紧密程度, 或者说项目在这个潜变量上的区分度。cj表示下渐近概率, 多项选择项目中通常解释为猜测概率, 心理测量的项目还反映了项目内容的模糊或晦涩程度。表示项目截距, 它与项目的难度或位置参数bj负相关。

3.1.2 多级评分双因子项目反应模型

对多级评分项目而言, 令K表示项目的反应类别数,表示项目反应,表示类别截距, 则在Samejima (1969)提出的等级反应模型基础上结合双因子模型假设, 可得双因子等级反应模型。它首先计算作答反应大于等于类别k (k=0,1,2,…,K−1)的概率, 即：

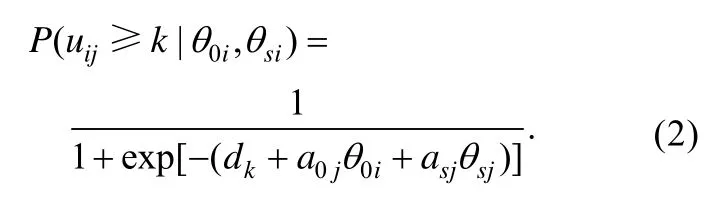
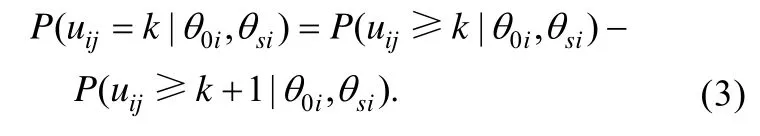
等级反应模型从累积概率出发计算类别反应概率属于两步模型, 分部评分模型和称名反应模型直接计算类别作答概率属于 divide-by-total模型。其中, 分部评分模型有多种等价表示方式, 在双因子模型假设下对Muraki (1992)中单维分部评分模型进行扩展, 得到如下双因子分部评分模型：

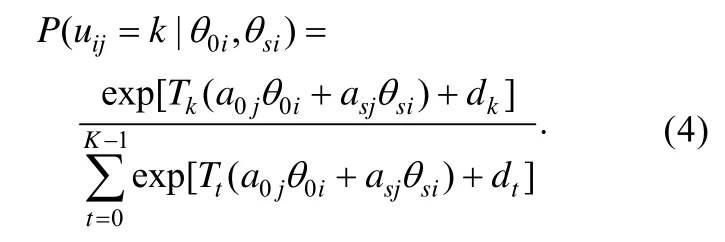
其中,Tt称为类别t的评分函数, 解释为评分者分配给反应类别t的分数, 通常取值为t。注意到, 如果给每个dk加上常数m, 类别反应概率将保持不变, 因而不能直接估计类别截距。为解决参数估计问题, 通常限制某个类别截距(如d0)等于0。

分部评分模型中通过事先规定有序的评分函数的值, 从而使K个反应类别有一定的优劣次序。实际上, 某些项目的反应与特质类型有关, 项目反应并不具备严格次序。这时, 称名反应模型就非常适合了。 称名反应模型同(4)式, 其评分函数的值通过估计而得, 描述了能力线性组合条件下反应类别间的次序。Thissen, Reeve, Bjorner和Chang (2007)曾将该模型用于探索病人自我报告数据中反应类别的等级次序。总体上, 称名反应模型是最灵活的 IRT参数模型之一, 它能很好地代表项目反应过程。同分部评分模型一样, 估计称名反应模型的类别截距参数时通常假设第一个类别截距为0。

3.2 参数估计

双因子项目反应理论模型作为验证性项目因素分析模型, 可运用Mplus、NOHARM、IRTPRO、FlexMIRT等软件估计模型参数, 也可以根据马尔可夫链蒙特卡洛方法或最大边际似然估计方法的思想编辑程序来估计模型参数。特别地, Gibbons和 Hedeker (1992)在运用最大边际似然估计方法估计项目参数时提出的“维度缩减”方法是全信息项目双因子分析的重要特征。下面以最大边际似然估计为例介绍“维度缩减”思想。

该方法首先将能力视为无关参数将其从似然函数中积分出来, 得到项目参数的边际似然函数,然后在项目参数范围内对边际似然函数求最优,从而获得项目参数估计值。以图 1(e)中所示的双因子模型为例, 项目 1、2、3考察一般因子和第一个组因子, 项目4、5、6考察一般因子和第二个组因子。因为双因子模型下能力相互独立, 其联合概率分布为于是, 基于项目参数集合、项目作答概率和能力联合分布可得反应y的边际分布, 即：

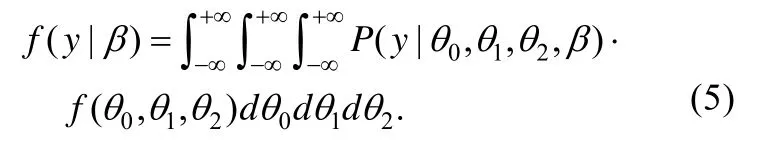
由于项目反应满足条件独立性, 于是

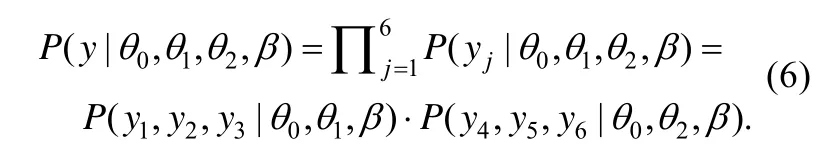
因为组因子相独立, 因而可将两个组因子维度先独立地在联合分布中积分, 然后对一般因子积分, 即

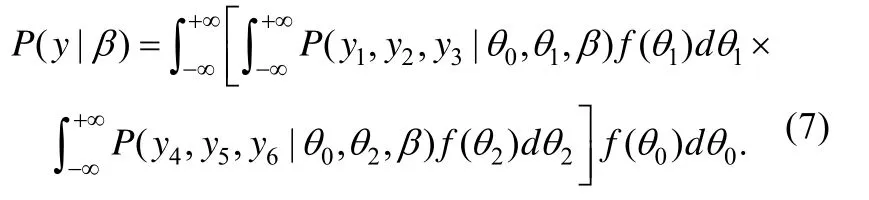
从而化简为二维迭代积分。特别地, 若每个维度固定20个积分节点, 这里只需要估计800个函数的值, 而直接积分则需要估计8000个函数的值。利用标准数值技术, 可以在范围中找到最优解,获得最大边际似然估计值

由此可见, 维度缩减思想就是对项目参数的边际似然函数在双因子模型假设下进行适当重组,进而化简积分方程(5)。一般地, 若有Q个特殊组因子, 每维度有P个积分节点, 则维度缩减方法只需要计算个函数值, 而直接积分需要计算个函数值。由此可见, 维度缩减方法大大简化了积分计算的复杂度。

3.3 双因子项目反应理论模型简评

双因子项目反应模型是多维项目反应模型在双因子模型假设下的特殊形式, 具有多维项目反应模型的一般特征。例如, 双因子等级反应模型中类别反应概率是能力的增函数, 双因子分部评分模型和称名反应模型则由类别评分函数的值而定。若类别评分函数的值递增, 则类别反应概率是能力的增函数。反之能力高的被试在低得分类别上的反应概率可能更高, 在高得分反应类别的反应概率反而更小。又如, 分部评分模型通过事先给定评分函数的值, 成为称名反应模型的特例。特别地, 分部评分模型与等级反应模型对项目反应过程的假设不同, 但二者的项目特征曲线没有明显差异, 加之分部评分模型作为 divideby-total模型其计算更简单, 因而它常常代替等级反应模型分析实际数据。

上述双因子项目反应模型能够分析二级评分、有序评分和类别反应模式的项目, 特别是等级反应、分部评分和称名反应模型的提出显著提高了双因子模型的应用范围。统计上讲, 双因子模型的广泛应用应归功于维度缩减思想在参数估计中的应用。特别地, 双因子模型中能力独立的假设条件下对能力进行积分的计算都可以将Q个组因子能力维度先独立地求积分, 然后对一般因子维度积分, 从而将Q+1维积分简化为Q个二维迭代积分。双因子项目反应理论模型的提出和计算中维度缩减方法的实现将极大地推进双因子模型的应用。此外, Cai, Yang和Hansen (2011) 以及Cai (2010)在双因子模型的基础上扩展提出似双因子模型、多组双因子分析和两层模型。其中, 似双因子模型允许部分项目只在一般因子上有非零负载; 多组项目双因子分析不仅能估计各组被试潜特质的均值和方差, 还能判断项目在不同组之间是否存在项目功能差异等问题; 两层模型则是囊括了双因子模型、多维IRT模型和题组反应模型在内的更一般的项目反应模型。

4 全信息项目双因子分析的应用

大量研究表明双因子模型符合认知能力、心理特质、精神病理等多类测验的结构特征。目前,全信息项目双因子分析已广泛应用于探索和验证测验或量表的维度结构、检验一般因子与组因子对项目的贡献、评估被试的能力水平以及CAT中。

4.1 在分析测验结构中的应用

虽然项目反应理论是一个广受欢迎的分析量表结构的方法, 在探索测验结构时, 研究者仍大量采用传统线性因素分析方法。例如, Watkins和Beaujean (2014), Dombrowski, Canivez, Watkins和Beaujean (2015)分别使用验证性和探索性双因子模型检测韦氏智力量表的因素结构, 研究表明一般因子解释了大部分共有的子测验方差, 组因子解释的方差比例可以忽略不计, 双因子结构比Wechsler (2012, 2014)提出的高阶智力结构更符合数据事实。又如, Colwell, Gordon, Fujimoto, Kaestner和 Korenman (2013)以及 Hindman, Pendergast和Gooze (2016)指出照顾者交互量表(Caregiver Interaction Scale, CIS)测量了一个一般因子和两个方法因子。另外, 传统双因子因素分析还用于分析自我领导结构(Furthner, Rauthmann, & Schse,2015)、研究测量活力及相关概念题库的结构(Deng, Guyer, & Ware, 2015)、分析学校适应不良行为(Wiesner & Schanding, 2013)、教育成就动机(Cham, Hughes, West, & Im, 2015)以及家庭作业的功能(Power, et al., 2015)。这些研究都表明双因子模型符合许多心理学、病理学和教育学测验特征, 具有广泛的应用前景。

尽管传统线性因素分析方法能够快速处理数据, 但全信息项目分析方法克服了传统线性因素分析中高估维度、低估负荷的缺陷, 并能在因素分析中考虑猜测参数等优势(俞宗火, 2005)。特别地, 全信息双因子分析运用“维度缩减”方法极大地降低了计算复杂度显著减少计算时间。因而,全信息项目双因子分析已越来越多地被用到教育和心理测验维度研究。例如, 消费者保健计划评估调查(Consumer Assessment of Healthcare Providers and Systems, CAHPS)数据的分析(Reise, et al.,2007)、精神病诊断筛选测验(psychiatric diagnostic screening questionnaire, PDSQ)因素结构的分析(Gibbons, Rush, & Immekus, 2009)、barratt冲动量表结构的分析(Steinberg, Sharp, Stanford, & Tharp,2013)以及State Metacognitive Inventory的维度评估(Immekus & Imbrie 2008)。其中, Reise等(2007)发现, 尽管单维IRT模型、相关特质多维IRT模型和双因子模型对 CAHPS提供了相似拟合度,但双因子模型分析的结果表明项目反应违反了局部独立性假设, 并且当去掉一般因子的方差解释量时, CAHPS项目不再充分测量每个子量表特质。这种情况下, 单维 IRT的分析结果将存在偏差, 即可能扭曲或歪曲被试的评分, 而多维分析中的两个维度实质上共同反映了一个更一般的能力因子。因此, 他们指出双因子模型允许研究者考察单维模型在拟合多侧面数据时的失真情况和考证多维分析中各子量表的有用性。上述研究都表明双因子模型能帮助澄清和解释给定测验、问卷或量表的结构, 很多情况下比其它竞争模型(如单维、高阶和相关特质模型)能更准确地反映量表维度。

4.2 在分数解释中的应用

双因子模型中组因子往往是研究者不感兴趣的无关因子, 而双因子模型能控制一些难以分离的干扰因子的影响更准确地解释一般特质。例如,Rijmen (2010)在分析国际英语评估数据时将项目组领域的相关作为特殊因子控制后分析整体英语能力水平。事实上, 大部分教育测验项目都是围绕一定的生活背景, 而并没有呈现出有意义的认知能力, 如果控制这些无关因素将会得到更有意义的特质分数。反过来, 研究者也可能对控制一般因子之后特殊因子的分数感兴趣。例如, 在一项幼儿园评估中, Betts, Pickart和Heistad (2011)就在控制一般因子之后考察了文学和数字两个组因子是否能够预测今后的阅读和数学成就。特别地, DeMars (2013) 建议当控制一般因子后只有存在足够的信度去解释子量表分数时使用子量表分数才有意义, 否则不建议使用子量表分数。

4.3 在CAT中的应用

如前所述, 全信息项目双因子分析已广泛应用于分析心理量表、病人自我报告、教育调查问卷以及教育评估测验获得的数据, 加之CAT技术的成熟及其实践应用, 探索双因子模型下CAT的理论、技术和方法开拓了全信息项目项目双因子分析应用的新领域。目前, 有关双因子模型 CAT的研究很少, 主要包括双因子模型CAT的实现和选题策略的研究。

首先, Weiss和Gibbons (2007)以双因子模型题库为基础将CAT分为多个阶段, 每个阶段测量一种能力实现了双因子测量结构在单维CAT中的应用。具体来讲, 第一阶段在所有项目中选择题目, 获得一般能力和领域能力估计值, 以后各阶段分别以第一阶段中领域能力估计值作为能力初值在各个子量表领域选择项目, 获得各个子组能力的估计值。他们通过多个来自615个人格测量项目的数据集证明在保证CAT能力估计值与全量表能力估计值的相关大于0.9时, 双因子CAT中一般因子的平均测验长度缩短了 95%, 各个内容领域的测验长度减少了68%到90%。总体上讲, 与纸笔测验相比, 双因子CAT的平均测验长度减少了80%, 实际节省约82%的测验时间。其次, Zheng,Chang和Chang (2013)采用Weiss和Gibbons (2007)的双因子CAT方法, 考察了内容约束条件对测量精度和项目使用率的影响。

上述研究都是在单维情况下开展双因子 CAT,通过多阶段CAT实现多维能力评估, 并没有实现在CAT中的直接应用双因子项目反应模型。鉴于此, Seo (2011)将传统多维CAT项目选择方法和能力估计方法应用到双因子 IRT模型, 实现多维双因子模型CAT。Seo和Weiss (2015)进一步在低双因子结构、高双因子结构和似双因子结构下比较了D-优化、Ds优化, A优化和E优化四种项目选择方法。Seo (2011) (Seo & Weiss, 2015)的研究呈现了双因子模型下项目选择和能力估计的特点,为双因子模型CAT的相关研究打下基础。

4.4 全信息项目双因子分析应用简评

首先, 全信息项目双因子分析中双因子模型提供了一个极好的测量结构框架, 在探索和验证测验结构时具有一些独特性。例如, 双因子模型通过分离一般因子和组因子对项目集合的贡献,更容易解释因子含义、检测项目是否违背局部独立性假设、发展子量表并指明多维量表中分量表的信度和有用性。当多个采用了相同反应类别、措辞、表述特征的项目集合带来的方法效应解释了控制主要因素之后独特的方差时, 双因子模型能检测非研究目的的方法性方差, 并指出这些项目如何捆绑在一起, 从而更好地澄清工具的维度结构。特别地, 双因子模型通过识别方法效应不仅提高了模型拟合统计, 还能帮助识别有实质意义的维度, 而这些维度可能在传统探索性因素分析中受到方法效应的影响而被掩盖。值得注意的是, 虽然双因子模型假设测验考察一个主要维度,但当测验显示出很强的单因子结构时不适合使用双因子模型。同样, 当项目在多个组因子维度有负载时也不适合使用双因子模型。只有当研究者有很强的理论证据支持所考察领域的双因子结构或者有证据表明双因子结构比其他模型更适合的时候采用双因子模型才更有意义。

其次, 全信息项目双因子分析中双因子项目反应模型关注被试在不相关的一般特质和多个领域因子上的表现, 这与多维项目反应理论模型通常在多个相关领域上对个体进行评定不同。因而,全信息项目双因子分析依赖能够在一定程度上准确测量那些独立于一般因子的多个特定领域因子的测验。这一点上, 双因子 IRT模型与其它多维IRT模型相比, 一方面能更清楚解释特质的含义,另一方面却不能提高测验效率。

再次, 全信息项目双因子分析在CAT中的应用也具有一些特殊性。多维CAT中测验考察的维度越多, 能力估计和项目选择的计算越复杂。当多维CAT中运用二阶因子模型时, 其参数估计的效率和复杂性同样会受到一阶潜特质因子数量的限制。而双因子IRT模型中假设一般因子与组因子正交、组因子之间正交能极大地简化有关能力的积分运算, 例如简化CAT中期望后验能力估计和项目信息量(Kullback-Leibler信息量、互信息、连续熵)的计算。于是, 当多维CAT中运用双因子IRT模型时, 其受因子个数的影响不大。另外, 双因子IRT模型中一般因子和组因子都是一阶因子,因而双因子IRT模型下CAT的计算不比单维CAT更复杂多少, 与此同时双因子IRT模型下CAT与其它多维CAT相比并不会提高CAT的测验效率。

5 研究展望

全信息项目双因子分析中双因子模型要求每个项目测量一般因子和一个组因子, 并假设能力相互正交, 是一类特殊的多维模型。首先, 双因子模型中不相关因素结构能解释独特的因素方差变异量, 而相关特质多维模型中只能获得共享的因素方差变异量。其次, 双因子模型将题目变异分解为一般因子变异、领域组因子变异和误差变异,测验的同质性信度和内部一致性信度的计算也具有特殊性(顾红磊，温忠麟，方杰, 2014)。再次, 双因子模型通过指明一般因子与组因子的地位克服了二阶因子模型中对高阶因子解释的不确定性和模糊性, 通过考察一般因子和组因子对项目变异的解释量还能检验模型的单维性假设。全信息项目双因子分析结合了双因子模型和项目反应理论模型, 具备二者的优势和特征。目前, 全信息项目双因子分析在验证测验结构方面已得到广泛应用,但对双因子项目反应模型的相关研究, 如：参数估计、模型特征、量表连接、项目功能差异、模型和项目拟合以及CAT应用方面都还有待开展深入研究。

首先, 针对双因子项目反应理论模型参数估计问题, 还缺乏系统研究考察参数估计中选用不同初始值或不同先验分布的效应; 缺乏研究考察违反特定假设时参数估计的结果; 也需要进一步探讨不同估计方法的特点, 系统比较它们在各种测验条件下的估计结果。

其次, 分析双因子项目反应理论模型下项目特征曲线和条件项目类别特征曲线, 不仅可以解释能力如何影响项目作答反应, 还能比较不同被试群体中能力对项目反应的影响是否相同。Toland, Sulis, Giambona, Porcu和Campbell (2017)描述了双因子等级反应模型中条件项目类别特征曲线和信息函数的定义、特征及其解释。由于项目信息函数在不同模型下的表达式不同, 因而推导双因子项目反应理论模型下信息函数的计算对分析项目与测验特征, 开展CAT都极其重要。另外, 分析测验信息与测验中不同项目类型的比例之间的关系将对测验组卷具有重要指导意义。

再次, 双因子 IRT模型下量表连接、项目功能差异检验也都具有特殊性。众所周知, 测验考察维度越多, 量表连接和项目功能差异的检验都越复杂。如果研究者只对一般因子感兴趣, 而忽视组因子维度, 那么标准的量表连接方法在双因子模型下就显得容易了。Cai等(2011)曾对项目功能差异检验的似然比检验方法和Langer (2008)描述的 Wald方法进行调整后适用于双因子模型。另外, Fukuhara和Kamata (2011)基于题组项目提出双因子多维项目反应理论模型项目功能差异检验模型; Somerville (2012) 提出全信息项目双因子分析中五步题组项目功能差异检测方法。特别地, 双因子模型将一般因子和组因子分离开来,将更容易解释项目功能差异的来源。此外, IRT背景下已有大量模型拟合指标和项目拟合指标, 如Li和Rupp (2011)讨论了全信息项目双因子模型中S− χ2在检验个人拟合中的表现。在双因子测验结构下检验这些指标的性能、提出新的模型和项目拟合指标都显得格外重要。

最后, 双因子IRT模型下CAT作为全信息项目双因子分析的一个重要的应用领域还有很多实际问题值得进一步研究。例如, 考察双因子 IRT模型下Kullback-Leibler信息量选题方法、香农熵和互信息等选题方法在一般能力维度和领域能力维度的选题表现; 又如, 考察在是否具有无关能力维度, 是否关注线性能力组合条件下比较选题方法的表现; 再如, 探索双因子 IRT模型下 CAT中项目曝光控制和内容约束、探索双因子IRT模型下混合测验CAT中多级评分项目的比例和呈现方式如何影响测验表现、题库增补等都是有意义的研究问题。

顾红磊, 温忠麟, 方杰.(2014).双因子模型: 多维构念测量的新视角.心理科学, 37(4), 973–979.

俞宗火.(2005).FIFA方法及其与CLFA方法在EPQ因素分析中的比较研究(硕士学位论文).江西师范大学, 南昌.

Betts, J., Pickart, M., & Heistad, D.(2011).Investigating early literacy and numeracy: Exploring the utility of the bifactor model.School Psychology Quarterly, 26(2), 97–107.

Cai, L.(2010).A two-tier full-information item factor analysis model with applications.Psychometrika, 75(4), 581–612.

Cai, L., Yang, S., & Hansen, M.(2011).Generalized fullinformation item bifactor analysis.Psychological Methods,16(3), 221–248.

Canivez, G.L.(2016).Bifactor modeling in construct validation of multifactored tests: Implications for understanding multidimensional constructs and test interpretation.In K.Schweizer & C.DiStefano (Eds.),Principles and methods of test construction: Standards and recent advancements.Gottingen, Germany: Hogrefe Publishers.

Cham, H.N., Hughes, J.N., West, S.G., & Im, M.H.(2015).Effect of retention in elementary grades on grade 9 motivation for educational attainment.Journal of School Psychology,53(1), 7–24.

Chen, F.F., West, S., & Sousa, K.(2006).A comparison of bifactor and second-order models of quality of life.Multivariate Behavioral Research, 41(2), 189–225.

Colwell, N., Gordon, R.A., Fujimoto, K., Kaestner, R., &Korenman, S.(2013).New evidence on the validity of the Arnett caregiver interaction scale: Results from the early childhood longitudinal study-birth cohort.Early Childhood Research Quarterly, 28(2), 218–233.

DeMars, C.E.(2006).Application of the bi-factor multidimensional item response theory model to testletbased tests.Journal of Educational Measurement,43(2),145–168.

DeMars, C.E.(2013).A tutorial on interpreting bifactor model scores.International Journal of Testing, 13(4),354–378.

Deng, N.N., Guyer, R., Ware, J.E., Jr.(2015).Energy,fatigue, or both? A bifactor modeling approach to the conceptualization and measurement of vitality.Quality of Life Research, 24(1), 81–93.

Dombrowski, S.C., Canivez, G.L., Watkins, M.W., &Beaujean, A.A.(2015).Exploratory bifactor analysis of the Wechsler Intelligence Scale for Children—Fifth Edition with the 16 primary and secondary subtests.Intelligence,53, 194–201.

Fukuhara, H., & Kamata, A.(2011).A bifactor multidimensional item response theory model for differential item functioning analysis on testlet-based items.Applied Psychological Measurement, 35(8), 604–622.

Furthner, M.R., Rauthmann, J.F., & Schse, P.(2015).Unique self-leadership: A bifactor model approach.Leadership,11(1), 105–125.

Gibbons, R.D., Bock, R.D., Hedeker, D., Weiss, D.J.,Segawa, E., Bhaumik, D.K., Kupfer, D.K.,...Stover, A.(2007).Full-information item bifactor analysis of graded response data.Applied Psychological Measurement, 31(1),4–19.

Gibbons, R.D., & Hedeker, D.R.(1992).Full-information item bi-factor analysis.Psychometrika, 57(3), 423–436.

Gibbons, R.D., Rush, A.J., & Immekus, J.C.(2009).On the psychometric validity of the domains of the PDSQ: An illustration of the bi-factor item response theory model.Journal of Psychiatric Research, 43, 401–410.

Hindman, A.H., Pendergast, L.L., Gooze, R.A.(2016).Using bifactor models to measure teacher-child interaction quality in early childhood: Evidence from the caregiver interaction scale.Early Childhood Research Quarterly, 36,366–378.

Holzinger, K.J., & Swineford, F.(1937).The bi-factor method.Psychometrika, 2(1), 41–54.

Immekus, J.C., & Imbrie, P.K.(2008).Dimensionality assessment using the full-information item bifactor analysis for graded response data: An illustration with the state metacognitive inventory.Educational and Psychological Measurement, 68(4), 695–704.

Langer, M.M.(2008).A reexamination of Lord’s Wald test for differential item functioning using item response theory and modern error estimation(Unpublished doctorial dissertation).University of North Carolina at Chapel Hill.

Li, Y., & Rupp, A.A.(2011).Performance of thestatistic for full-information bifactor models.Educational and Psychological Measurement, 71(6), 986–1005.

Muraki, E.(1992).A generalized partial credit model:Application of an EM algorithm.Applied PsychologicalMeasurement, 16(2), 159–176.

Power, T.J., Watkins, M.W., Mautone, J.A., Walcott, C.M.,Coutts, M.J., & Sheridan, S.M.(2015).Examining the validity of the homework performance questionnaire:Multi-informant assessment in elementary and middle school.School Psychology Quarterly, 30(2), 260–275.

Reise, S.P.(2012).The rediscovery of bifactor measurement models.Multivariate Behavioral Research, 47(5), 667–696.

Reise, S.P., Morizot, J., & Hays, R.D.(2007).The role of the bifactor model in resolving dimensionality issues in health outcomes measures.Quality of Life Research,16,19–31.

Rijmen, F.(2009).Efficient full information maximum likelihood estimation for multidimensional IRT models(Tech.Rep.No.RR-09-03).Princeton, NJ: Educational Testing Service.

Rijmen, F.(2010).Formal relations and an empirical comparison among the bi-factor, the testlet, and a secondorder multidimensional IRT model.Journal of Educational Measurement, 47(3), 361–372.

Samejima, F.(1969).Estimation of latent ability using a response pattern of graded scores(Psychometric Monograph No.17).Richmond, VA: Psychometric Society.

Schmid, J., & Leiman, J.M.(1957).The development of hierarchical factor solutions.Psychometrika, 22(1), 53–61.

Seo, D.G.(2011).Application of the bifactor model to computerized adaptive testing(Unpublished doctorial dissertation).The University of Minnesota.

Seo, D.G., & Weiss, D.J.(2015).Best design for multidimensional computerized adaptive testing with the bifactor model.Educational and Psychological Measurement,75(6), 954–978.

Somerville, J.T.(2012).Detection of differential item functioning in the generalized full-information item bifactor analysis model(Unpublished doctorial dissertation).University of California, Los Angeles.

Steinberg, L., Sharp, C., Stanford, M.S., & Tharp, A.T.(2013).New tricks for an old measure: The development of the Barratt Impulsiveness Scale-Brief (BIS-Brief).Psychological Assessment, 25(1), 216–226.

Thissen, D., Reeve, B.B., Bjorner, J.B., & Chang, C.-H.(2007).Methodological issues for building item banks and computerized adaptive scales.Quality of Life Research, 16,109–119.

Toland, M.D., Sulis, I., Giambona, F., Porcu, M.&Campbell, J.M.(2017).Introduction to bifactor polytomous item response theory analysis.Journal of School Psychology,60, 41–63.

Watkins, M.W., & Beaujean, A.A.(2014).Bifactor structure of the Wechsler Preschool and Primary Scale of Intelligence-Fourth edition.School Psychology Quarterly, 29(1), 52–63.

Wechsler, D.(2012).Wechsler preschool and primary scale of intelligence(4th ed.).Bloomington, MN: Pearson.

Wechsler, D.(2014).Wechsler intelligence scale for children(5th ed.).Bloomington, MN: Pearson.

Weiss, D.J., & Gibbons, R.D.(2007).Computerized adaptive testing with the bifactor model.Paper presented at the New CAT Models session at the 2007 GMAC Conference on Computerized Adaptive Testing.Retrieved from http://www.iacat.org/sites/default/files/biblio/cat07weiss%26gibbons.pdf

Wiesner, M., & Schanding, G.T.(2013).Exploratory structural equation modeling, bifactor models, and standard confirmatory factor analysis models: Application to the BASC-2 behavioral and emotional screening system teacher form.Journal of School Psychology, 51(6), 751–763.

Yung, Y.-F., Thissen, D., & McLeod, L.D.(1999).On the relationship between the higher-order factor model and the hierarchical factor model.Psychometrika, 64(2), 113–128.

Zheng, Y., Chang, C.-H., & Chang, H.H.(2013).Contentbalancing strategy in bifactor computerized adaptive patient-reported outcome measurement.Quality of Life Research, 22, 491–499.