中主应力系数对岩石强度准则的影响

傅鹤林，史越，龙燕，张加兵，黄震



中主应力系数对岩石强度准则的影响

傅鹤林1, 2，史越1, 2，龙燕1, 2，张加兵1, 2，黄震1, 2

(1. 中南大学土木工程学院，湖南 长沙，410075；2. 中南大学 高速铁路建造技术国家工程试验室，湖南 长沙，410075)

为揭示真三轴条件下的岩石强度，基于Mohr−Coulomb准则、Hoek−Brown准则、Drucker−Prager准则、Mogi−Coulomb准则、统一强度理论等不同本构模型，引入中主应力系数，推导不同强度准则关于的计算公式；结合Mogi对Dunham白云岩试样的试验结果，将该问题等效为不同本构模型在变化下的比选问题。研究结果表明：随着增加，当3较小时，统一强度理论比较适用，在统一强度理论计算峰值与试验峰值之间Mogi−Coulomb准则和Hoek−Brown准则比较适合；当3较大时，Mogi−Coulomb准则失效，Hoek−Brown准则较为安全；采用统一强度理论在岩石强度峰值之后能较好地拟合试验曲线；Drucker−Prager外接圆准则主要适用于一般三轴条件下或较小情况下的计算。

中主应力系数；岩石强度；本构模型；强度准则

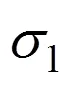
1 基本理论

1.1 中主应力系数

定义中主应力系数为

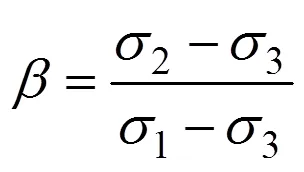
在弹塑性理论中，常以Lode参数表示应力参数：

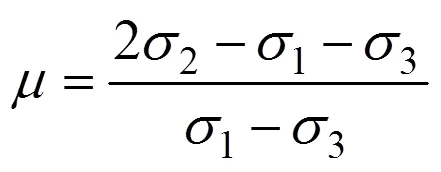
不难证明，和之间满足如下关系：

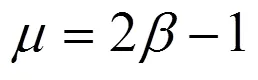
1.2 Mohr−Coulomb准则

1900年提出的Mohr−Coulomb(简称M−C)准则实际上只考虑了1个剪应力及其面上正应力，没有考虑中主应力对土抗剪强度的影响或者说中主应力对土抗剪强度无关。单剪强度理论是各种可能外凸理论的 下限。

在平面应力状态下，M−C屈服准则可表示为：

1.3 Hoek−Brown准则

Hoek和Brown于1980年针对完整、黏聚力很强的岩石和岩体提出了Hoek−Brown(简称H−B)强度准则[11−12]，为了使其更具普遍性与适用性，于1997年又提出了广义H−B准则[13]：

其中：

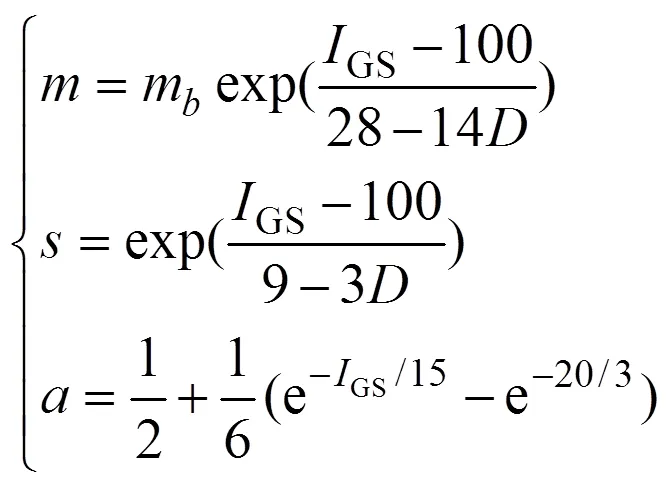
1998年SINGH等[14]提出修正的H−B准则：

结合式(1)和(8)为

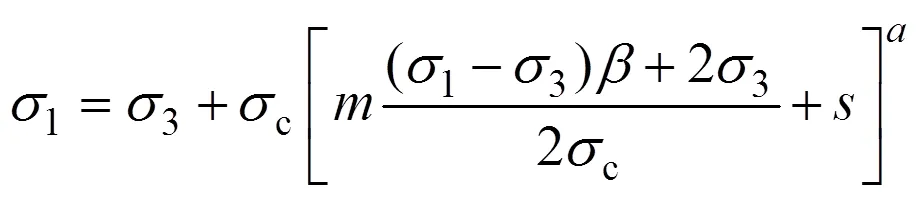
1.4 Drucker−Prager准则

在主应力空间，M−C屈服面为一不规则六棱锥面；在π平面内，为一不等角六边形。由于Drucker−Prager(简称D−P)屈服面在π平面内为一簇光滑圆曲线，表述简洁且计算效率高，因此，常用D−P系列准则逼近M−C准则。

以应力不变量表示D−P准则[6]：

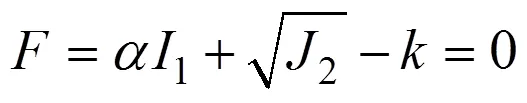
国外大型有限元软件(如ANSYS、MARC)通常把M−C外角点外接圆准则作为D−P准则，如图1所示。

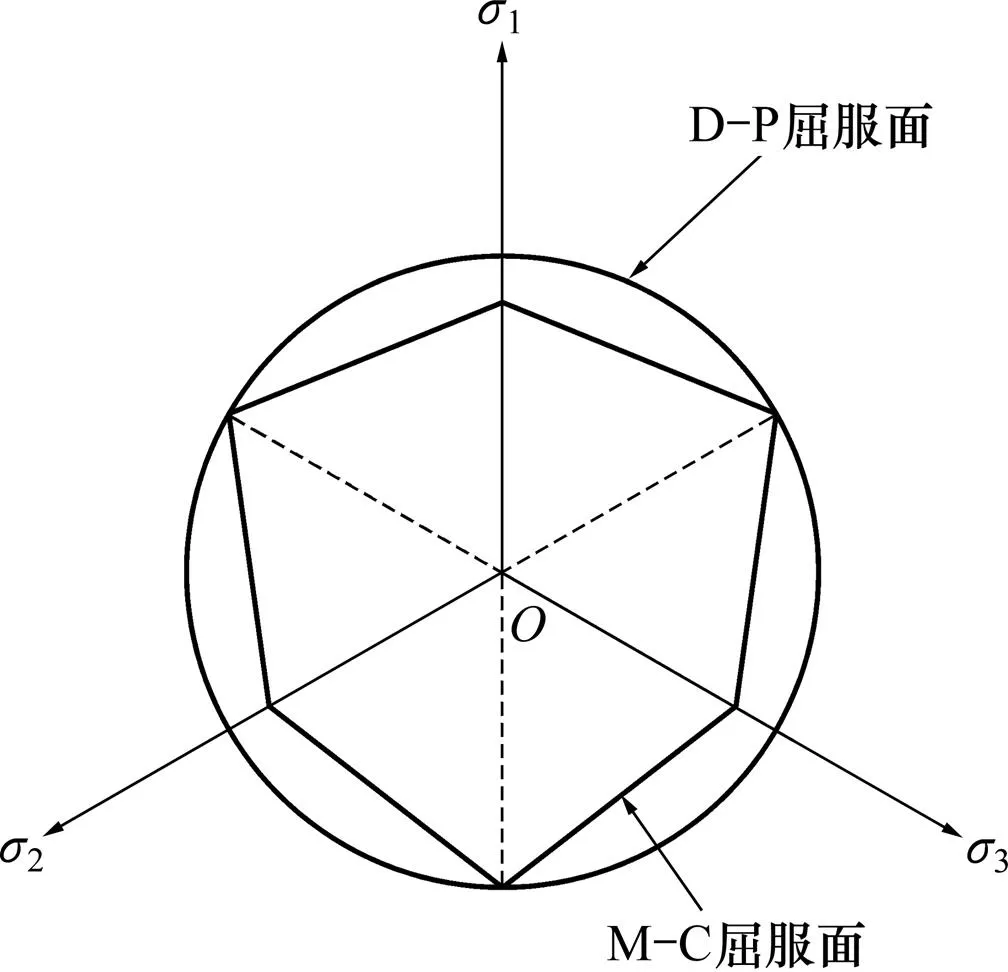
图1 π平面上M−C准则与D−P外接圆准则的关系

这时，有[15]

在真三轴情况下，结合式(1)和(11)，式(10)为

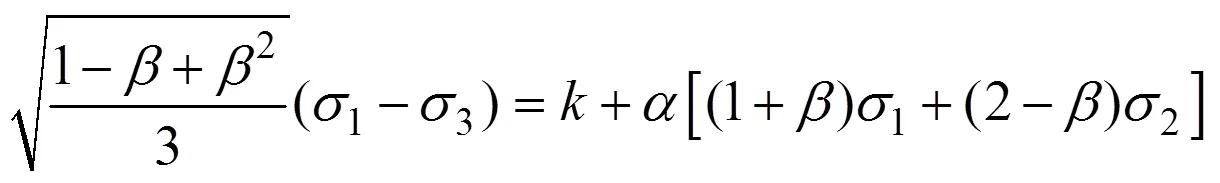
在一般三轴情况下(=0)，

化简可知，式(13)为M−C准则。

1.5 Mogi−Coulomb准则

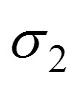
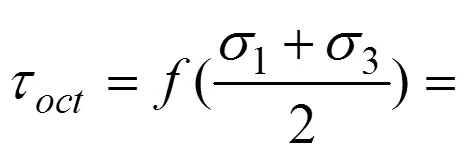
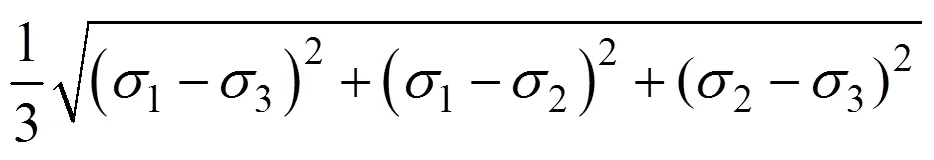
将Mogi经验强度准则与Coulomb强度准则相结合，AL-AJMI等[16]建立了Mogi−Coulomb(简称Mogi−C)强度准则：

其中：

结合式(1)和(16)，整理式(15)得[17]：

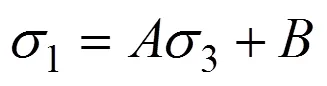
其中：

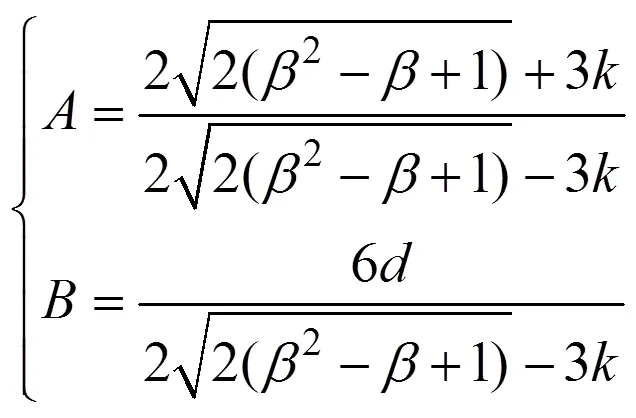
如上得到岩石强度与中主应力系数之间的关系式。π平面上M−C准则与Mogi−C准则的关系如图2所示，Mogi−C强度准则极限线为外接于M−C强度准则极限线的曲边六边形，在轴对称的三轴压缩状态(=0)和三轴拉伸状态(=1)即不考虑中主应力影响时，两准则的极限线重合。

图2 π平面上M−C准则与Mogi−C准则的关系

1.6 统一强度理论

1985年，俞茂宏等[7−8]建立了双剪强度理论，1997年，鲁祖统等[18]在数学上证明了单剪与双剪强度理论分别为各种屈服准则的内外包络线。

室内试验表明[19]，圆柱形岩石试样轴向压缩强度与围压大致成线性关系(和均为强度准则参数)：

若以相同的参数进行线性插值，则得到

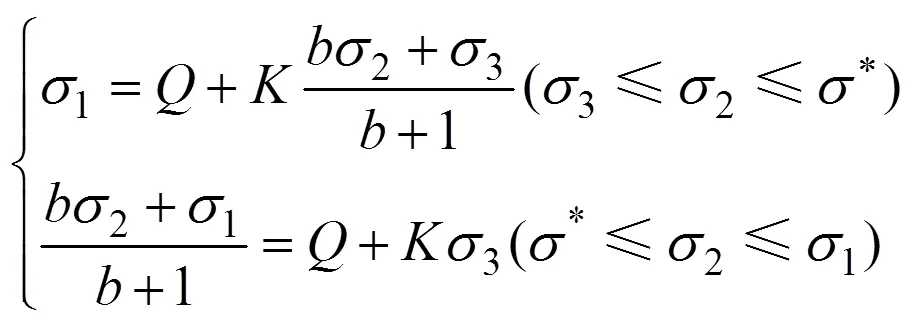
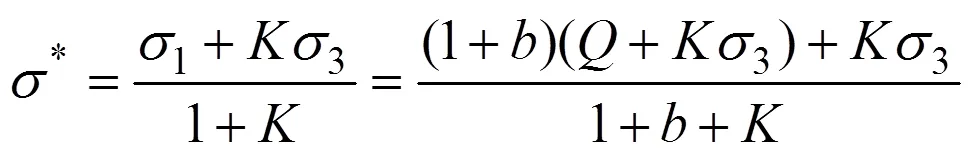
由式(20)分别整理得

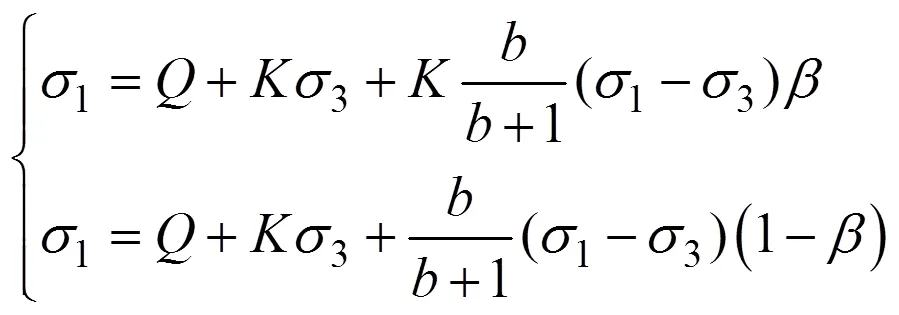
两式对比得

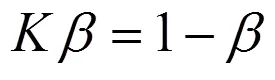
式(23)也为统一强度理论参数提供了算法，即为真三轴试验状态下岩石破坏时关于中主应力系数β的比值。

易得

此时岩石强度为

2 本构模型计算对比分析

表1 Mohr−Coulomb强度计算值

由1.2节及表1可知：M−C准则计算结果仅与小主应力有关，不随中主应力的改变而发生变化。随着中主应力的增加，保守性越来越明显，有必要通过多轴强度准则来进一步挖掘岩石强度的安全储备。

根据H−B准则相关参数回归分析的结果[20]，强度随中主应力系数计算结果如图3所示。M−C与H−B准则区别在于前者的破坏线在主应力空间的π平面及子午面上均为直线，而后者为曲线，因此，H−B准则可以很好地描述岩石强度的非线性特征，但难以确定准则中参数，特别是岩石各向异性明显时更限制了它的使用。

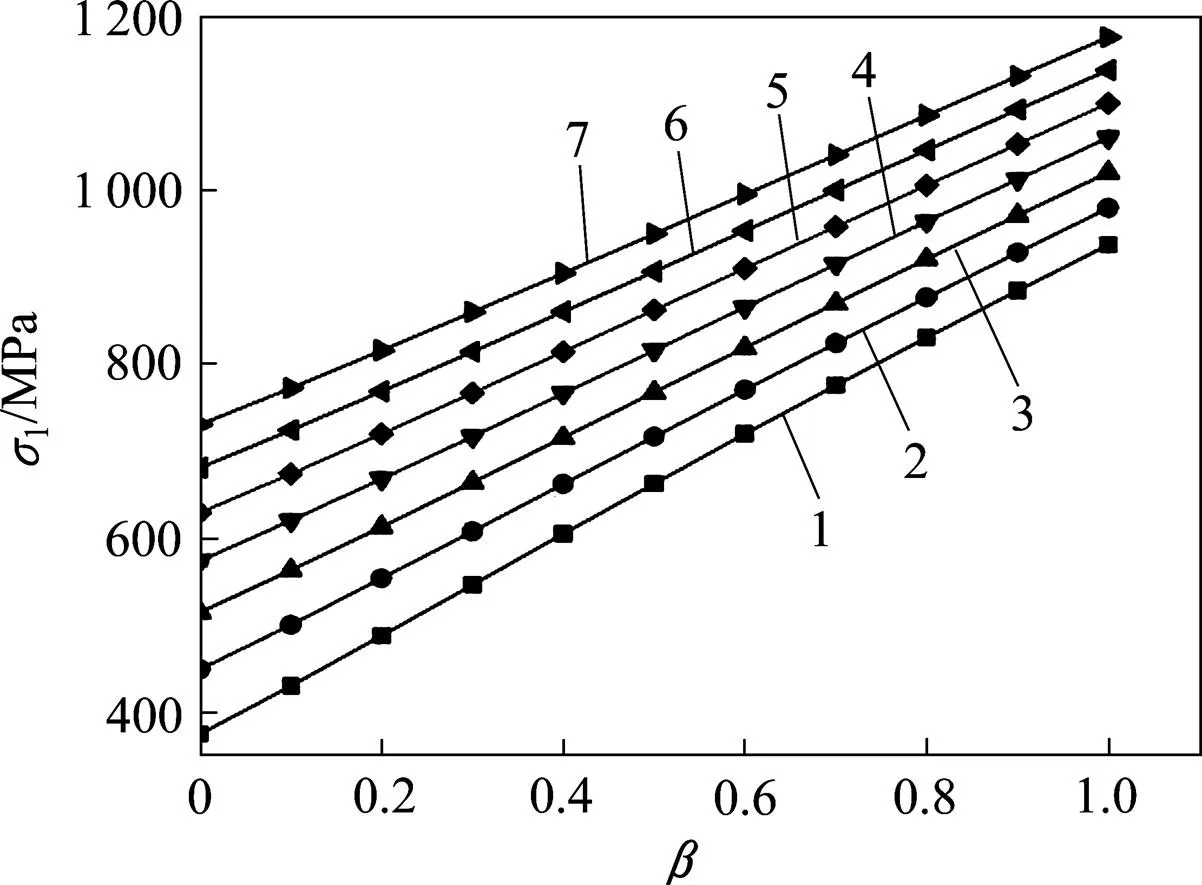
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

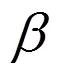
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

图5所示为Mogi−Coulomb准则强度曲线。根据岩石真三轴强度的统一强度理论参数(=298.9 MPa，=0.47)[19]，计算得到白云岩强度随变化曲线如图6所示。对比图5和图6可知：Mogi−C强度准则、统一强度理论考虑了中主应力作用效应及其作用的区间性，符合前述存在转折点的特征。但两强度准则在=0与=1时强度计算结果相等，这与试验结果不相符。其主要原因是两准则此时退化为不考虑中主应力效应的M−C准则。

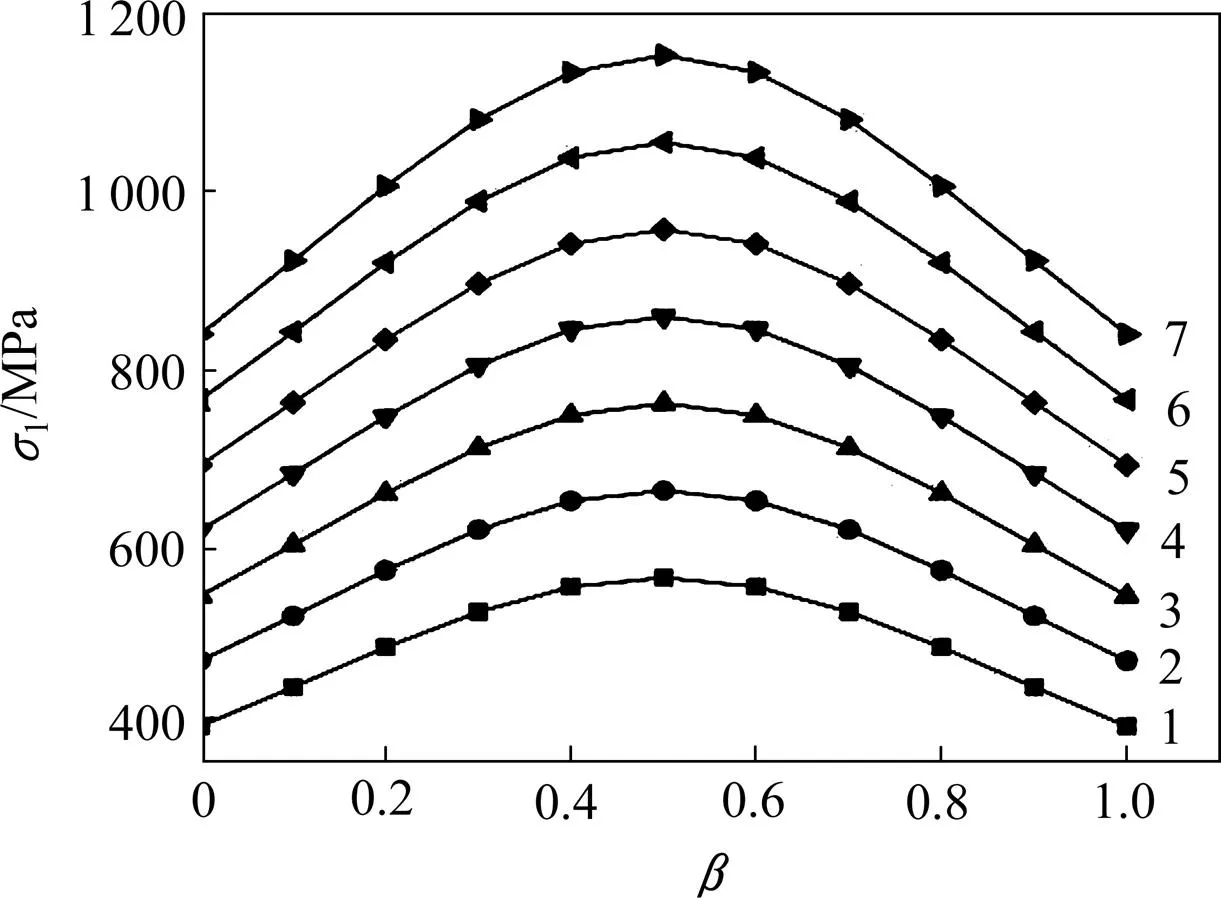
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

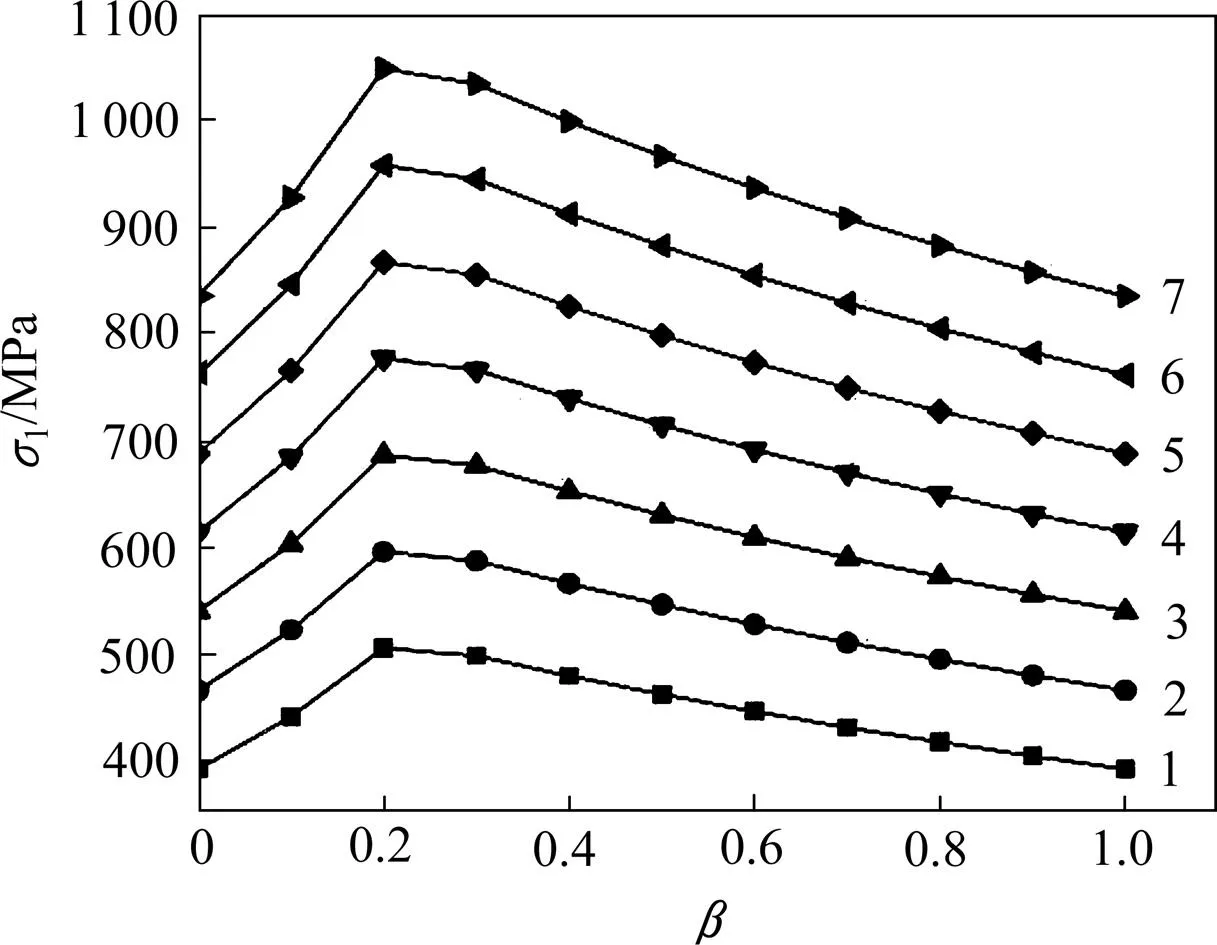
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

3 算例分析

3.1 试验数据分析

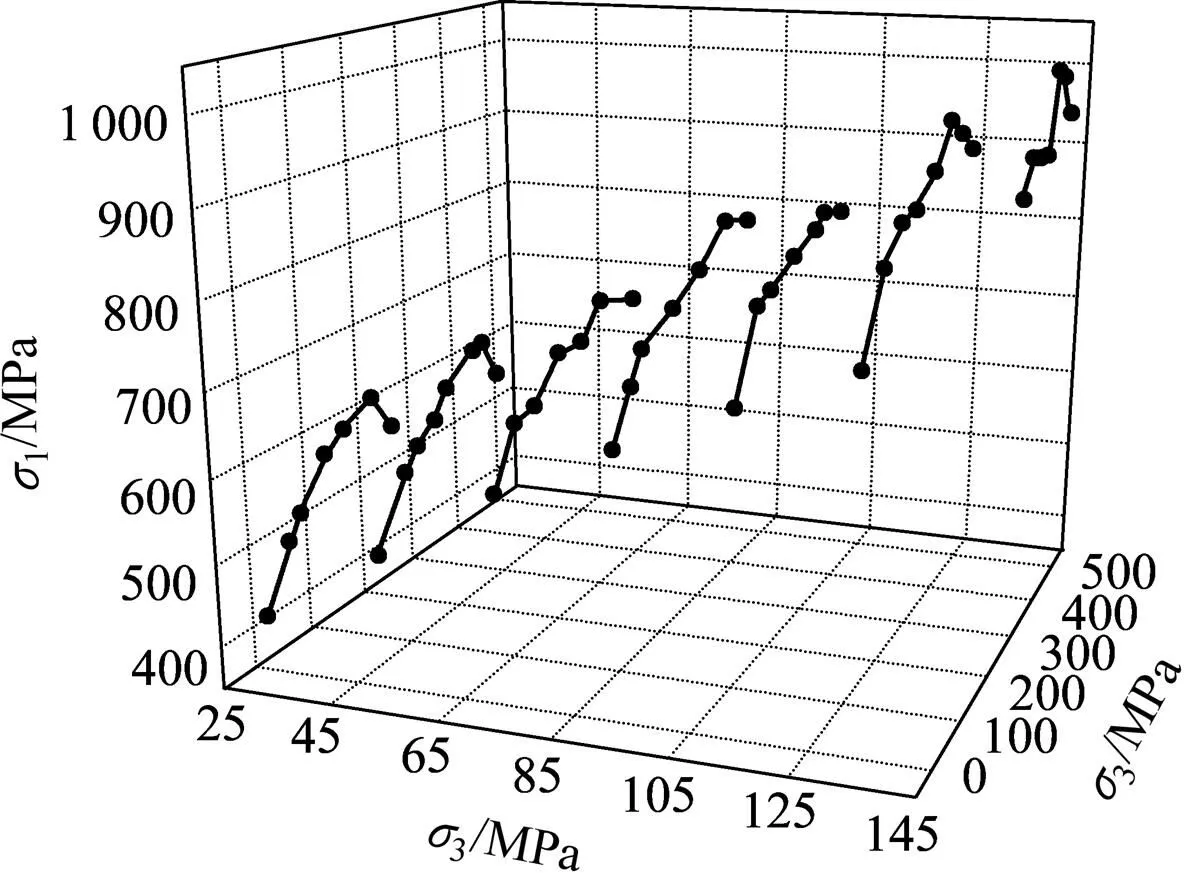
图7 Dunham 白云岩的真三轴试验数据

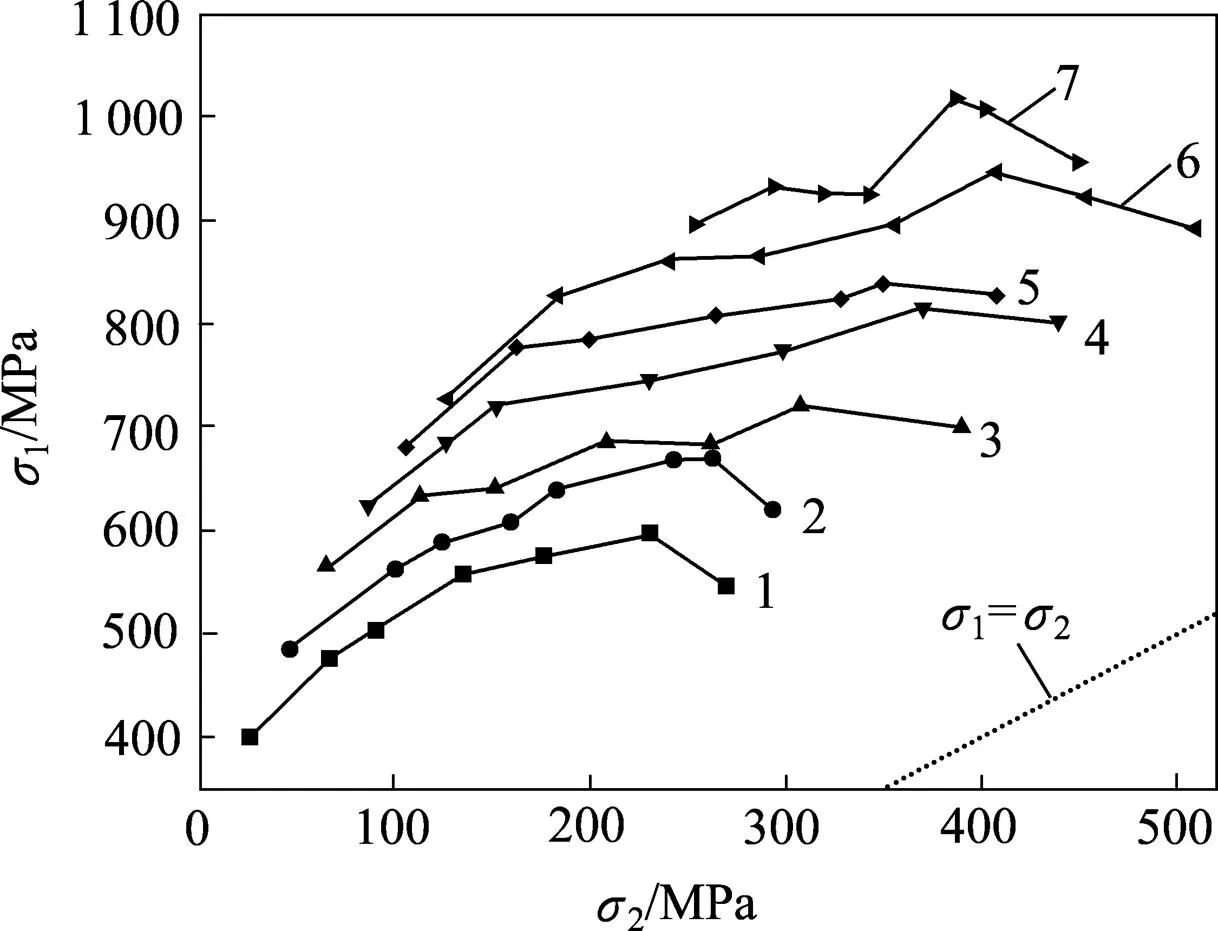
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

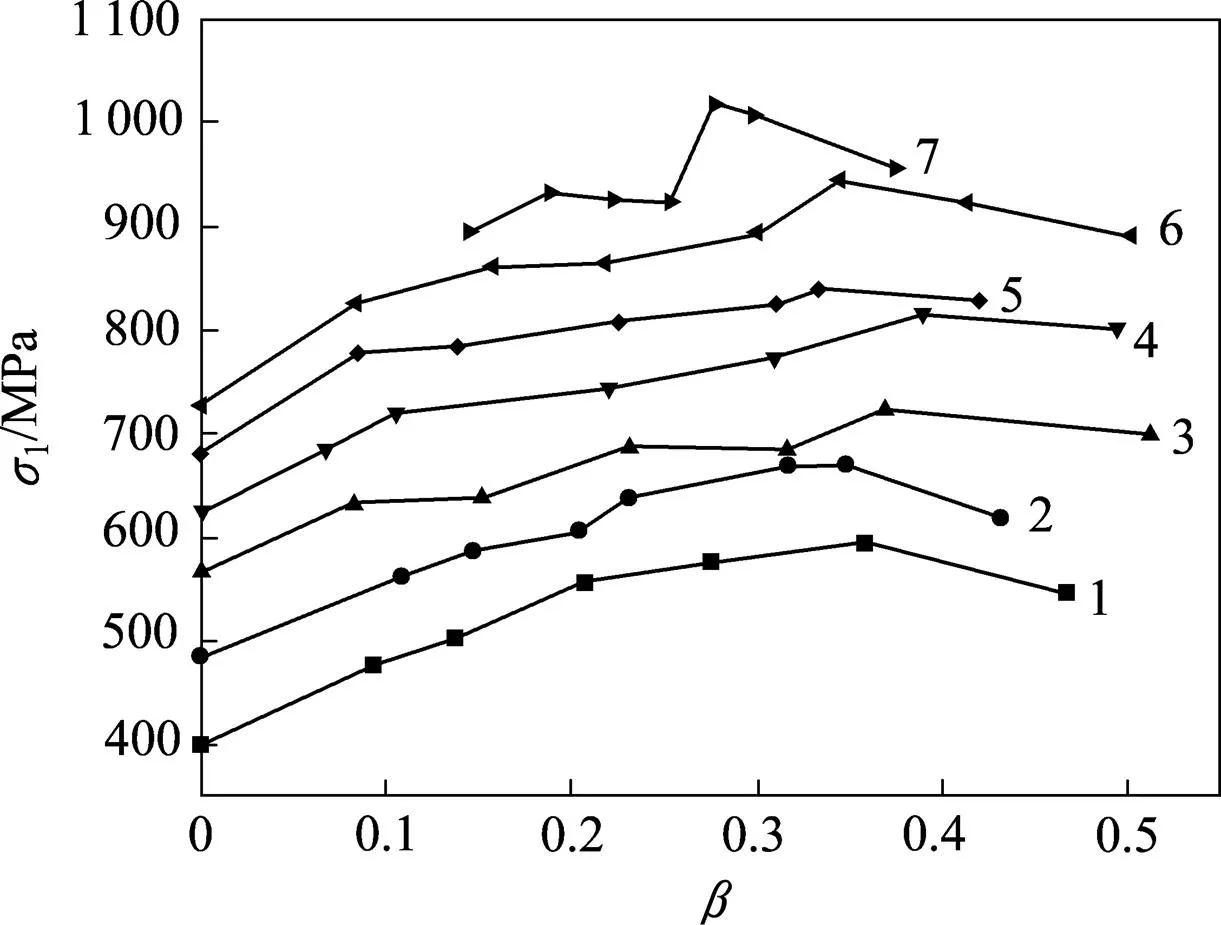
σ3：1—25；2—45；3—65；4—85；5—105；6—125；7—145。

3.2 中主应力系数β的影响

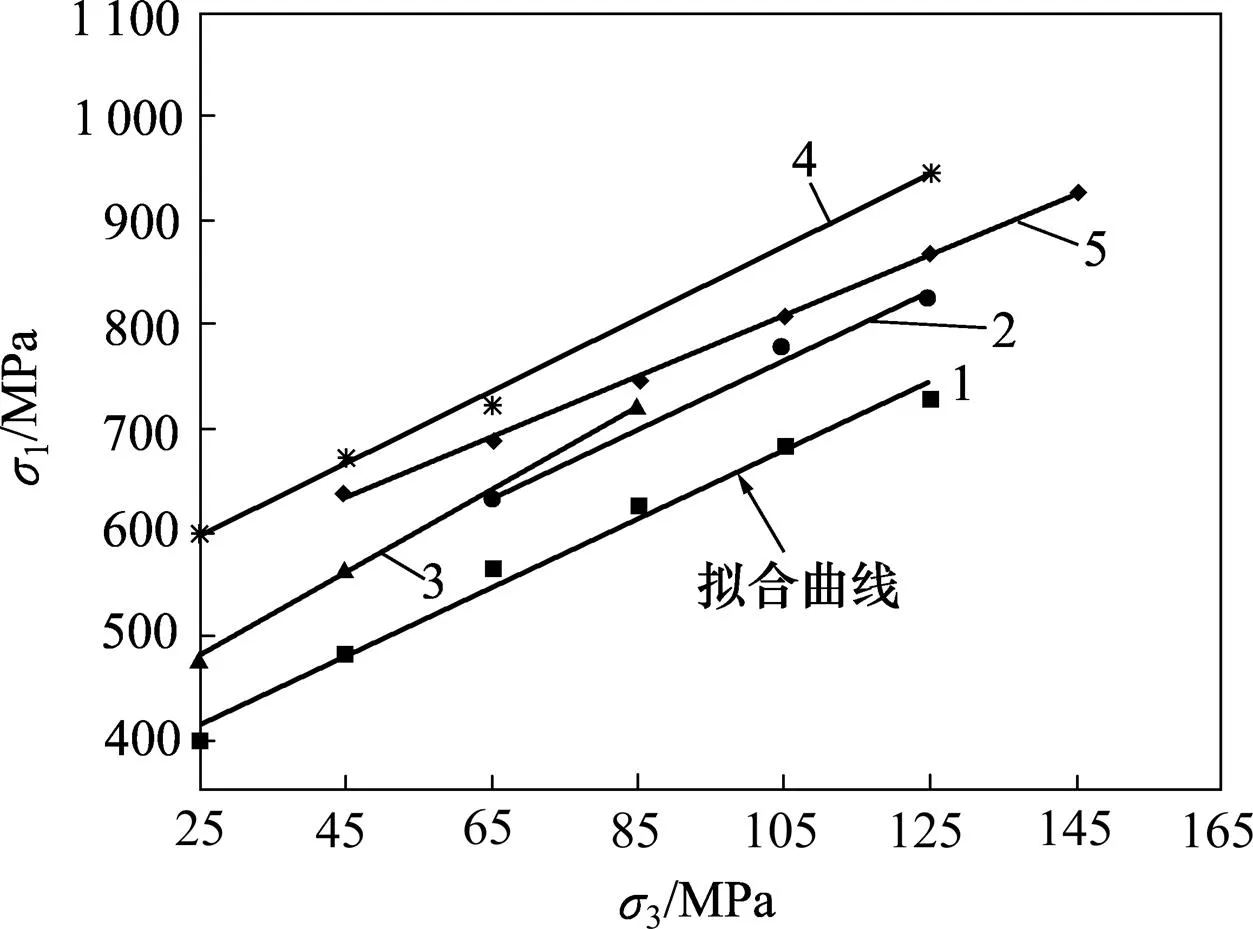
β：1—0；2—0.08；3—0.10；4—0.22；5—0.35。

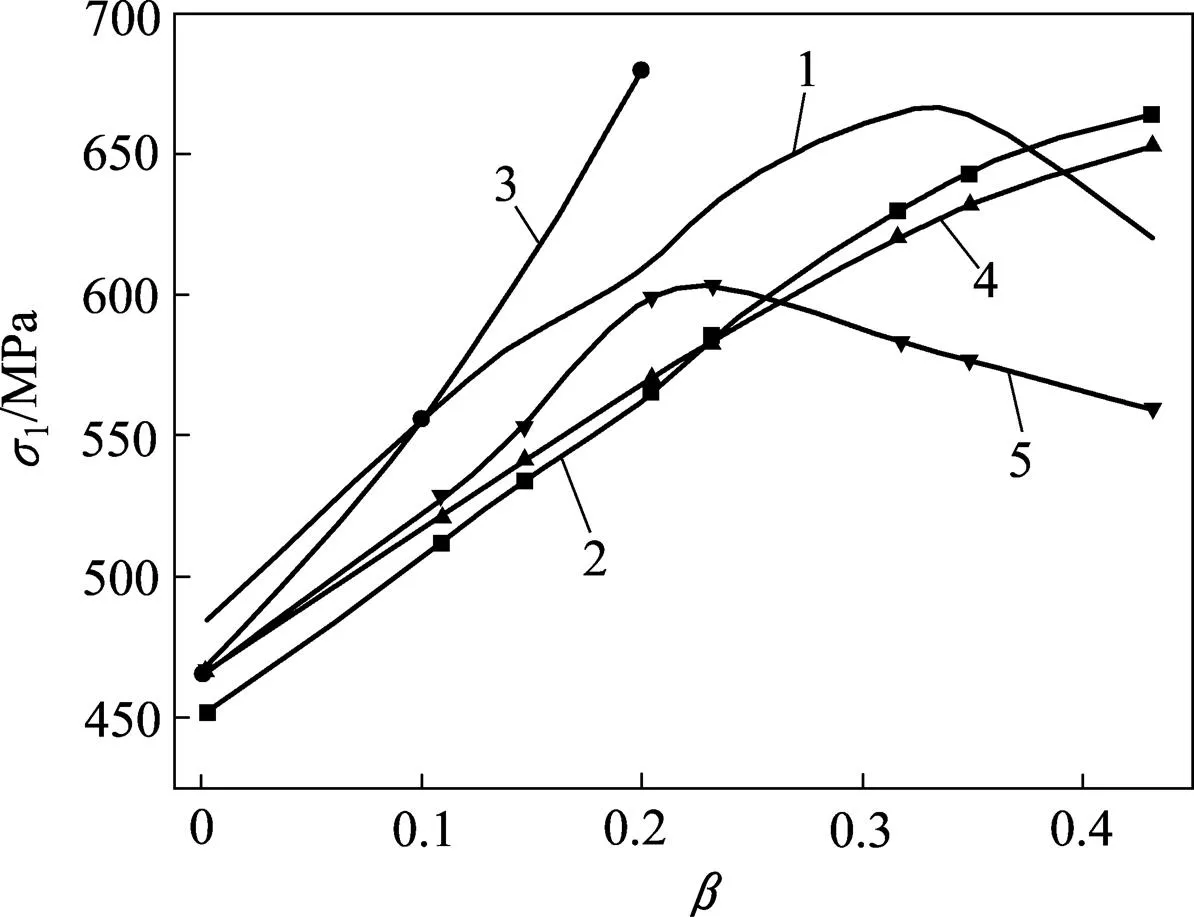
1—实验值；2—H−B准则；3—D−P准则；4—Mogi−C准则；5—统一强度理论。

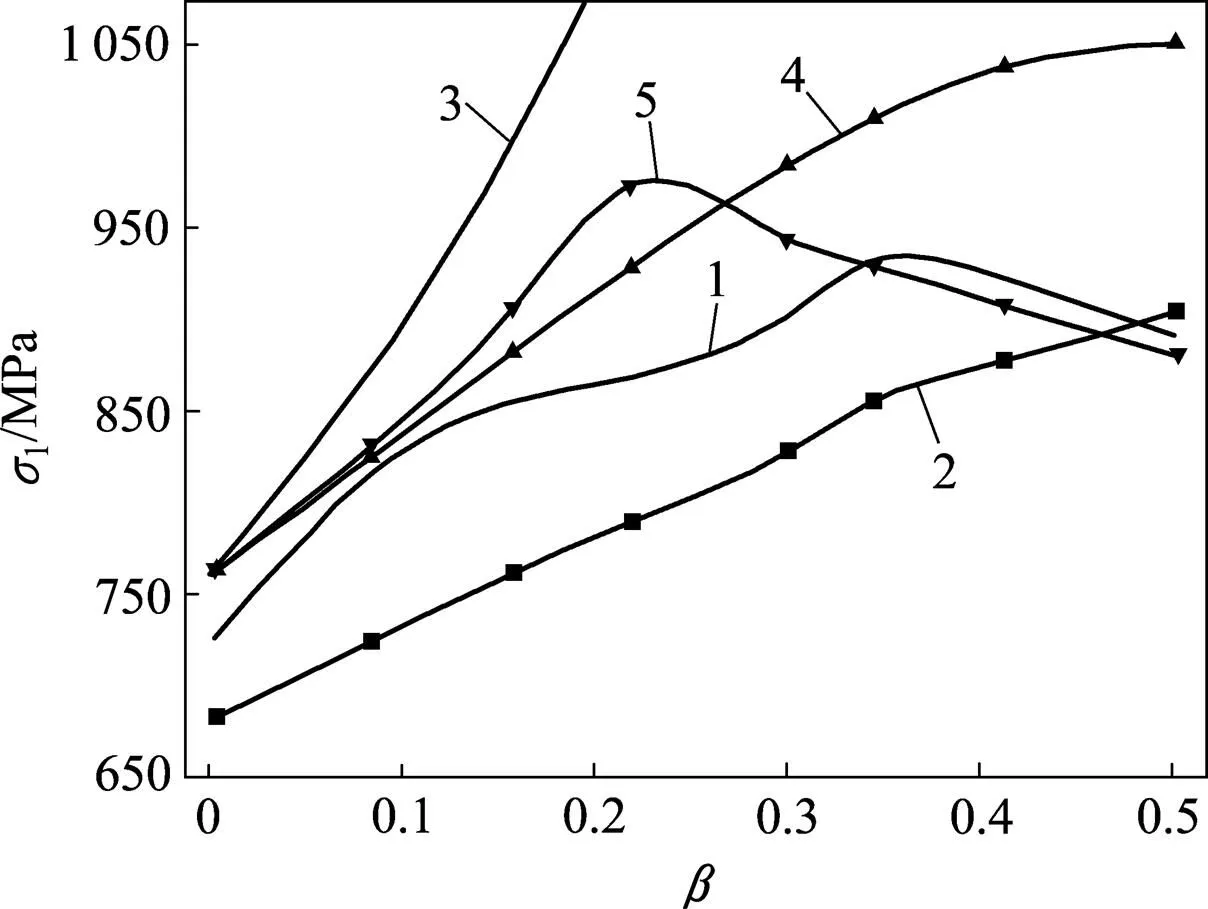
1—实验值；2—H−B准则；3—D−P准则；4—Mogi−C准则；5—统一强度理论。

从图11和12可知：D−P外接圆准则在较低地应力场且中主应力效应较小(图11，0＜＜0.10)时才能反映出岩石强度。

根据岩石强度随中主应力系数变化规律及上述讨论，在达到岩石最大强度对应的前(Dunham 白云岩的在0.35~0.40之间)，真三轴本构模型相比于目前大量应用的不考虑中主应力作用效应的M−C模型，能够更好反映出岩石强度变化规律，满足设计要求。

3.3 小主应力σ3的影响

根据前述试验数据的分析，岩石强度随小主应力的增大显著增大，拟合曲线为直线，Dunham 白云岩试验强度最大值对应范围在0.35~0.40之间。在这里分别取为0，0.10，0.22和0.40，用拟合曲线来比对试验值与不同的多轴本构模型计算值，如图13~16所示。

在一般三轴条件下(图13，=0)，M−C准则、D−P外接圆准则、Mogi−C准则、统一强度理论计算值相同，在低地应力场条件下小于试验值；随着增大(图14，=0.1)，D−P外接圆准则计算值在低地应力场内能够较准确的估算岩石强度，这与图10所示结果相吻合，反映出大部分有限元软件所内嵌的D−P外接圆模型较适合于一般三轴条件下的低地应力场计算。

1—实验值；2—M−C准则；3—H−B准则；4—D−P准则；5—Mogi−C准则；6—统一强度理论。

1—实验值；2—H−B准则；3—D−P准则；4—Mogi−C准则；5—统一强度理论。

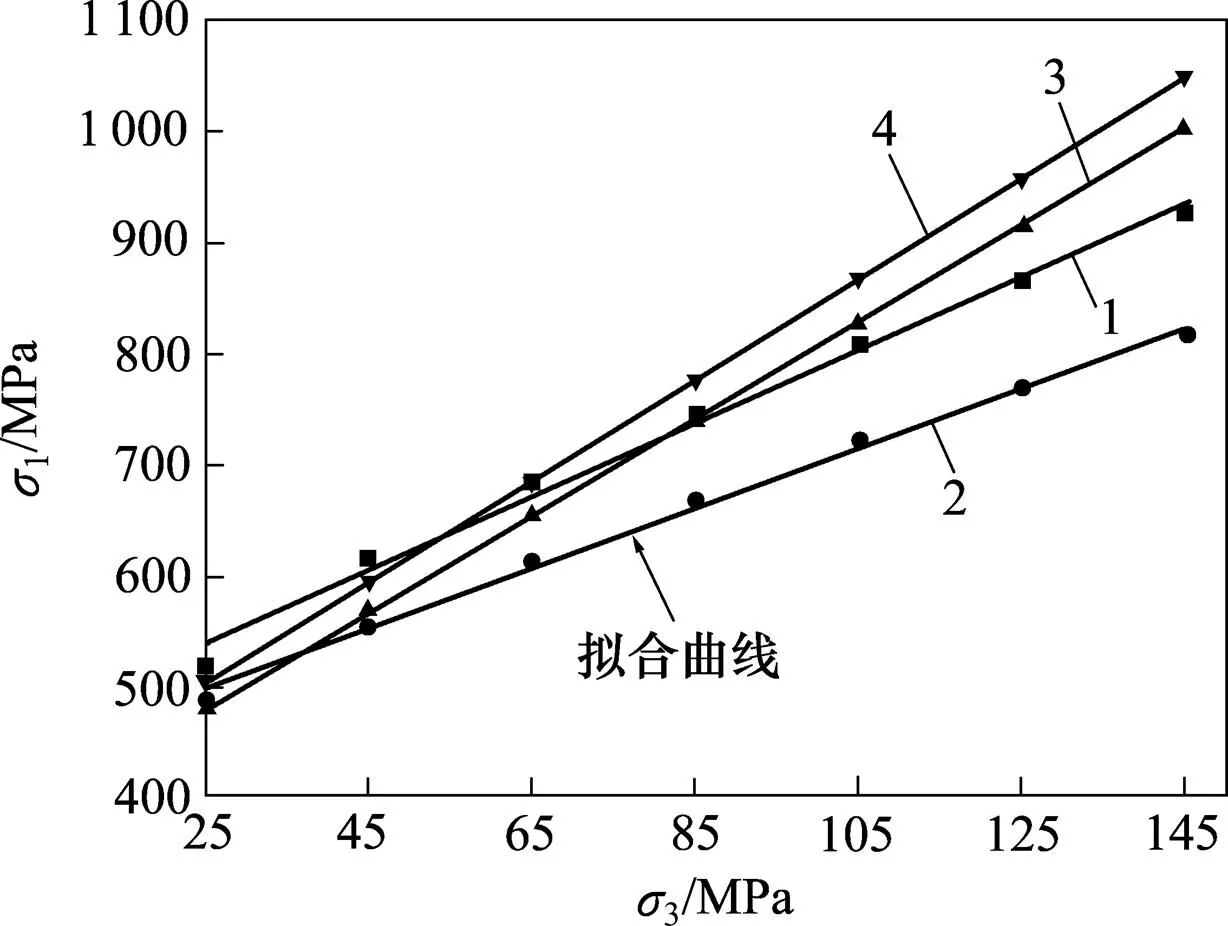
1—实验值；2—H−B准则；3—Mogi−C准则；4—统一强度理论。

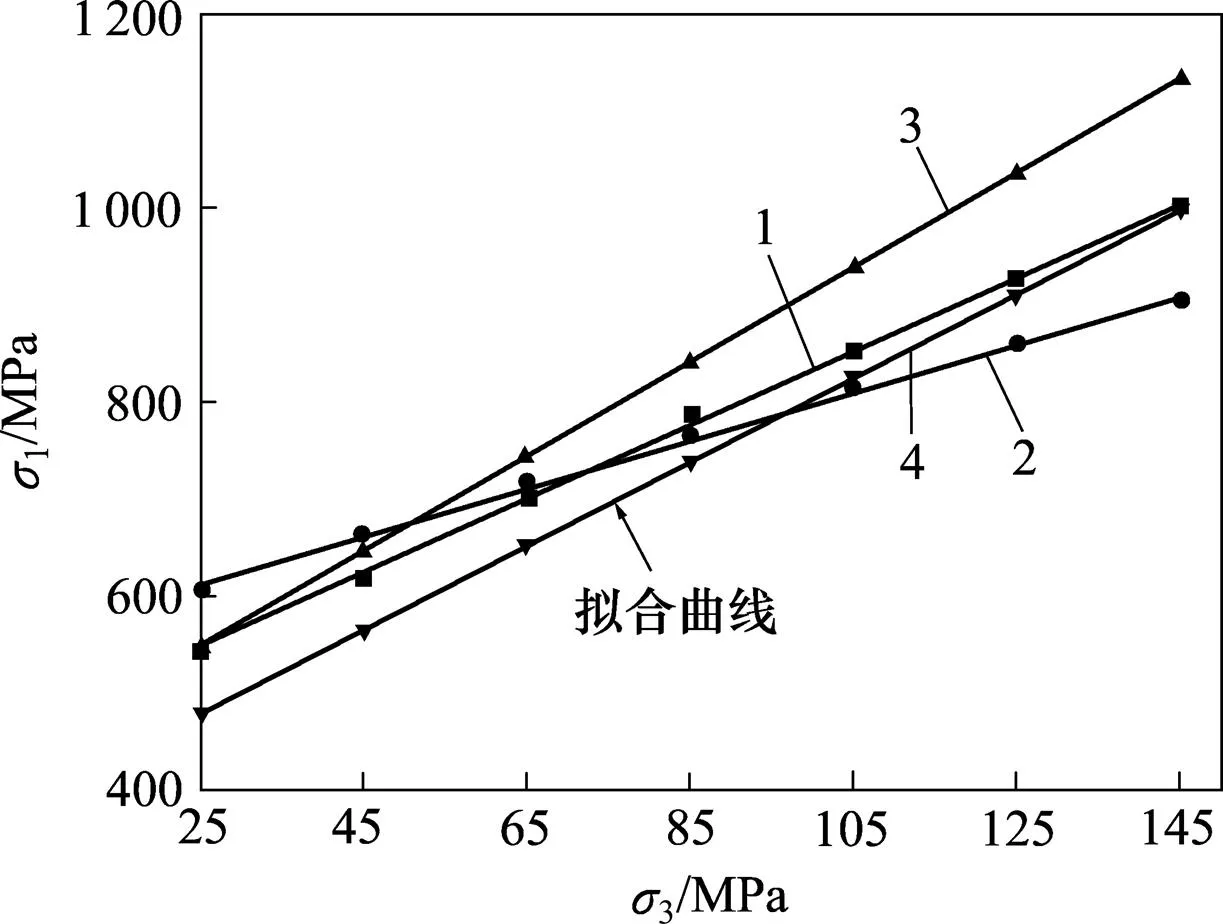
1—实验值；2—H−B准则；3—Mogi−C准则；4—统一强度理论。

根据岩石所处地应力场高低、强度峰前峰后、中主应力效应大小等条件，合理选择与转换不同的多轴本构模型，能够更进一步利用岩石的塑性储备。

4 结论

1) 基于中主应力系数定义，结合Hoek−Brown准则、统一强度理论，推导本构模型随变化的计算公式；并引用Drucker−Prager准则、Mogi−Coulomb准则计算模型随变化的计算公式，为真三轴条件下岩石强度随中主应力系数变化研究提供了理论依据。

2) 得到统一强度理论中参数的又一计算方法，即真三轴试验下岩石破坏时关于的比值，也说明了该系数的又一实用意义。

3) 对比真三轴条件下常用岩石本构模型随中主应力系数变化的计算曲线，在不考虑中主应力影响时，Drucker−Prager准则、Mogi−Coulomb准则、统一强度理论将退化为Mohr−Coulomb准则，计算值一致，Hoek−Brown准则计算值较小，反映出它的安全性。

4) 在低地应力场、很小时，各本构模型基本能够反映出岩石强度规律；在低地应力场，统一强度理论计算峰值之前(0.10＜＜0.20)，统一强度理论具有一定优越性；在统一强度理论峰值与试验强度峰值之间(0.20＜＜0.35)，Mogi−Coulomb准则和Hoek− Brown准则比较适用；在高地应力场复杂状态下，在岩石强度达到峰值之前(0＜＜0.35)，应用Hoek− Brown准则计算是偏于安全的；在岩石强度峰值之后(＞0.35)，统一强度理论能较好地拟合强度的变化。

5)广泛应用于有限元计算的Drucker−Prager外接圆准则仅在低地应力场一般三轴条件下或较小时(0＜＜0.10)才能较好地预测岩体强度，反映出该准则应用于岩土体计算的局限性。

6) 本文仅基于白云岩的试验数据，未对其他种类岩石展开分析，准则转换节点还需精确算核，因此，本文结论存在一定前提条件和局限性，有待进一步 探讨。

[1] MOGI K. Effect of the intermediate principal stress on rock failure[J]. Journal of Geophysics Research, 1967, 72: 5117−5131.

[2] MOGI K. Fracture and flow of rocks under high triaxial compression[J]. Journal of Geophysics Research, 1971, 76(5): 1255−1269.

[3] YAO Yangping, HU Jing, ZHOU Annan, et al. Unified strength criterion for soils, gravels, rocks, and concretes[J]. Acta Geotechnica, 2015, 10: 749−759.

[4] 许东俊, 耿乃光. 岩石强度随中间主应力的变化规律[J]. 固体力学学报, 1985, 6(1): 72−80. XU Dongjun, GENG Naiguang. The variation law of rock strength with increase of intermediate principal stress[J]. Acta Mechanica Solida Sinica, 1985, 6(1): 72−80.

[5] FU Helin, ZHANG Jiabing, HUANG Zhen, et al. A statistical model for predicting the triaxial compressive strength of transversely isotropic rocks subjected to freeze-thaw cycling[J]. Cold Regions Science and Technology, 2018, 145: 237−248.

[6] DRUNKER D C, PRAGER W. Soil mechanics and plastic analysis in limit design[J]. Quarterly of Applied Mathematics, 1952, 10: 157−165.

[7] 俞茂宏. 线性和非线性的统一强度理论[J]. 岩石力学与工程学报, 2007, 26(4): 662−669. YU Maohong. Linear and nonlinear unified strength theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 662−669.

[8] 昝月稳, 俞茂宏. 岩石广义非线性统一强度理论[J]. 西南交通大学学报, 2013, 48(4): 616−624. ZAN Yuewen, YU Maohong. Generalized nonlinear unified strength theory of rock[J]. Journal of Southwest Jiaotong University, 2013, 48(4): 616−624.

[9] 张传庆, 冯夏庭, 周辉. 岩石多轴与常规三轴强度的关系[J]. 固体力学学报, 2011, 32(3): 228−234. ZHANG Chuanqing, FENG Xiating, ZHOU Hui. Relationship between polyaxial strength and conventional triaxial strength for rock[J]. Chinese Journal of Solid Mechanics, 2011, 32(3): 228−234.

[10] 刘运思, 傅鹤林, 饶军应, 等. 基于 Hoek−Brown 准则对板岩抗拉强度研究[J]. 岩土工程学报, 2013, 35(6): 1172−1177. LIU Yunsi, FU Helin, RAO Junying, et al. Tensile strength of slate based on Heok−Brown criterion[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1172−1177.

[11] HOEK E, BROWN E T. Empirical strength criterion for rock masses[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1980, 106(9): 1013−1035.

[12] HOEK E, BROWN E T. Underground excavation in rocks[M]. London: Institution of Mining and Metallurgy, 1980: 527.

[13] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Science, 1997, 34(8): 1165−1186.

[14] SINGH B, GOELRK, MEHROTRA V K, et al. Effect of intermediate principal stress on strength of anisotropic rock mass[J]. Tunnelling and Under-ground Space Technology, 1998, 13(1): 71− 79.

[15] 唐芬, 郑颖人. 强度储备安全系数不同定义对稳定系数的影响[J]. 土木建筑与环境工程, 2009, 31(3): 61−65. TANG Fen, ZHENG Yingren. Effect on safety factors in different definitions based on strength margin[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(3): 61−65.

[16] AL-AJMI A M, ZIMMERMAN R W. Relation between the Mogi and the Coulomb failure criteria[J]. International Journal of Rock Mechanics and Mining Science, 2005, 42(3): 431−439.

[17] 吕彩忠. 基于Mogi−Coulomb强度准则的隧道围岩理想弹塑性解答[J]. 土木建筑与环境工程, 2014, 36(6): 54−59. LÜ Caizhong. Elastic-perfectly plastic solution of tunnel surrounding rocks using Mogi−Coulomb strength criteria[J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(6): 54−59.

[18] 鲁祖统, 龚晓南.关于稳定材料屈服条件在π平面内的屈服曲线存在内外包络线的证明[J].岩土工程学报, 1997, 19(5): 1−5. LU Zutong, GONG Xiaonan. Verification of inner and outer envelopes for the yield curve of stable material in π-plane[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 1−5.

[19] 尤明庆. 统一强度理论的试验数据拟合及评价[J]. 岩石力学与工程学报, 2008, 27(11): 2193−2204. YOU Mingqing. Fitting and evaluation of test data using unified strength theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(11): 2193−2204.

[20] 许宏发, 王发军, 江淼, 等. 岩石考虑中间主应力Hoek−Brown强度参数分析[J]. 解放军理工大学学报, 2012, 13(6): 636−639. XU Hongfa, WANG Fajun, JIANG Miao, et al. Parameters in Hoek−Brown’s failure criterion considering intermediate principal stress of rock[J]. Journal of PLA University of Science and Technology, 2012, 13(6): 636−639.

(编辑 杨幼平)

Influence of intermediate principle stress coefficient on rock strength criterion

FU Helin1, 2, SHI Yue1, 2, LONG Yan1, 2, ZHANG Jiabing1, 2, HUANG Zhen1, 2

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High Speed Railway Construction, Central South University,Changsha 410075, China)

To reveal the rock strength in the condition of true triaxial test, the intermediate principle stress coefficient was applied based on Hoek−Brown, Drucker−Prager, Mogi−Coulomb criterion and unified strength theory. With the modified strength criterion formulas referred toand the Dunham dolomite experiment data by Mogi, the problem was equivalent to contrasting and selecting different constitutive models appropriately. The results show that: With the increase of, the unified strength theory is suitable when the3is small, while Mogi−Coulomb criterion and Hoek−Brown criterion are appropriate when the related value ofranges between peak value calculated by unified strength theory and that of experiment; When the3is large, Mogi−Coulomb criterion is invalid and Hoek−Brown criterion is superior. After peak value of experiment condition, the unified strength theory is preferable in fitting the experiment value. Only in case of general triaxial or less value ofcan the Drucker−Prager circumcircle criterion fit experiment data better.

intermediate principle stress coefficient; rock strength; constitutive model; strength criterion

TU452

A

1672−7207(2018)01−0158−09

10.11817/j.issn.1672-7207.2018.01.021

2017−02−25；

2017−05−05

国家自然科学基金资助项目(51578550)；国家自然科学重点基金资助项目(51538009) (Project(51578550) supported by the National Natural Science Foundation of China; Project(51538009) supported by the State Key Program of National Natural Science of China)

史越，博士研究生，从事岩石力学和隧道工程等研究；E-mail: yueshi@csu.edu.cn