静载与冲击加载方式下滚刀破岩特性

谭青，劳同炳，张桂菊, 3，张旭辉，易亮，徐顺生



静载与冲击加载方式下滚刀破岩特性

谭青1, 2，劳同炳1, 2，张桂菊1, 2, 3，张旭辉1, 2，易亮1, 2，徐顺生4

(1. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083；2. 中南大学 机电工程学院，湖南长沙，410083；3. 邵阳学院机械与能源工程学院，湖南 邵阳，422004；4. 湘潭大学 机械工程学院，湖南 湘潭，411105)

为了研究在单一恒定静载荷和冲击动载荷这2种情况下盘形滚刀破岩机制，使用颗粒离散元法建立滚刀破岩的二维数值模型。通过控制破岩的垂直载荷，对滚刀破岩动态过程进行分析并研究静载荷、冲击动载荷和冲击次数对滚刀破岩特性的影响，最后通过实验对静载荷下滚刀破岩情形进行验证。研究结果表明：在单一恒定静载荷下，滚刀破岩效果随着静载荷增大而提高；当静载荷达到一定值后，破岩效果提升不明显，存在1个最佳静载荷使破岩效果最优；在冲击动载荷作用下，岩石裂纹扩展情况与静载荷的扩展情况相似，但岩石内部以剪切破坏为主；随着循环冲击动载荷以及施加次数增大，岩石内部产生的裂纹数增大并且有向水平贯穿的趋势，破岩比能耗先减少后变化不大；滚刀在动静载荷作用下比能耗的变化趋势基本一致，冲击动载荷破岩的比能耗比静载荷作用下的比能耗高，大约是静载荷破岩比能耗的1.4倍。

滚刀；颗粒流；破岩特性；比能耗；静载荷；冲击动载荷

在地下掘进过程中，盾构刀具直接参与掘进破岩的工作，因此，研究盾构刀具切削岩石的特性、分析不同切削岩石的方法对于高效破岩的意义十分重大。到目前为止，国内外众多学者对盾构刀具破岩机理开展了模拟建模和实验分析。LIU等[1]采用二维有限元仿真软件对滚刀侵入岩石过程进行了数值模拟，分析了岩石破碎过程的应力分布以及刀具的受力情况。刘建琴等[2]通过有限元软件对盘形滚刀回转破岩进行了仿真研究，优化设计了滚刀安装参数。夏毅敏等[3−4]使用有限元软件和离散元软件模拟分析了切削过程中岩石的破碎过程和切屑的形成过程。MOON等[5]通过颗粒离散元法从刀间距和切深的角度，研究了滚刀的最佳破岩情况。杨岳峰等[6]通过建立刀头冲击模型研究了冲击作用下岩石裂缝扩展情形。HUO等[7−8]通过动力学建模以及数值仿真对重载冲击作用下盘形滚刀及刀盘的振动特性进行了分析，并研究了滚刀切削过程的力学特性。金解放等[9]利用岩石动静组合加载霍普金森杆试验装置研究了不同轴压的岩石在循环冲击过程中动态强度和变形特性。赵伏军等[10]介绍了其自行设计研制的多功能动、静态耦合载荷破岩试验系统并且通过试验分析研究了动静载荷耦合破岩具体形式。上述研究成果对于研究盘形滚刀破岩机理有很大的参考价值，但对于静载荷与冲击动载荷作用下盘形滚刀破岩形态这一方面的研究往往局限于试验研究，而利用软件建模配合实验研究较少，且试验研究很难从微观角度观察到滚刀在载荷作用下的破岩效果。离散元技术可以从微观层面观察揭示其破岩机理，对于研究滚刀在静载荷和动载荷作用下的破岩机理具有重要意义。为此，本文作者在简化滚刀破岩过程的基础上，将刀圈运用球体Clump模型代替刚性墙模型[11]建立载荷边界条件下盘形滚刀破岩的离散元模型，并对模拟仿真结果进行分析，研究滚刀在不同载荷形式作用下的破岩形式。

1 盘形滚刀破岩数值模型

1.1 岩石数值模型的确定

在利用颗粒流程序建立模型过程中，颗粒流的细观参数需要一个标定过程使得其与材料的宏观物理力学参数一一对应。在一般情况下，通过单轴压缩和巴西劈裂数值试验对模型参数进行标定[12]。实验所使用的岩石来自广东省佛山市某采石场，按照岩石力学试验性能测试的标准制作了直径为50 mm、高为100 mm以及直径为50 mm，高为50 mm的圆柱试样以及边长为70 mm的正方体岩石试样。并对岩石试样几个端面进行打磨，使其垂直度和平行度均达到测试要求，对岩石的试样力学参数进行测试，得到岩石的力学性能参数如表1所示。

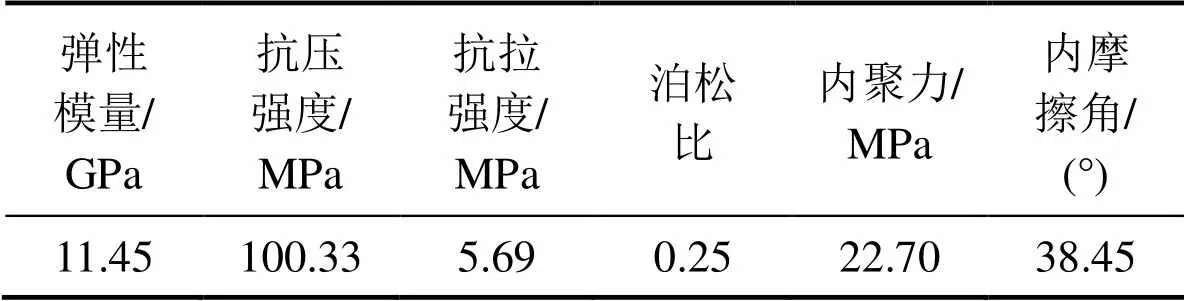
表1 硬岩材料宏观参数

在岩石试样数值模型模拟过程中，设定模型中的最大和最小颗粒半径之比为1.66，其中最小颗粒半径为8×10-4m。考虑到颗粒与颗粒之间存在孔隙，设定颗粒的密度为3.145 t/m3。在二维模型参数标定过程中，选取岩石试样尺寸为长×宽为100 mm×50 mm。

基于岩石试样力学试验性能测试，在颗粒流程序软件中对盘形滚刀破岩中的岩石进行单轴压缩和巴西劈裂的数值模拟，经过不断标定选取合适的细观参数去匹配表1中的宏观参数，得到此时岩石试样在PFC2D中的细观参数如表2所示。

表2 细观力学参数

1.2 滚刀载荷加载侵入破岩数值模型简化

随着盾构机刀盘的旋转与推进，盘形滚刀一方面在切向摩擦力的作用下作滚动运动，另一方面在刀盘推力作用下作直线侵入运动[13]。在盘形滚刀破岩过程中，岩石裂纹的产生与扩展的主导因素是主推力作用下的侵入运动。INNAURATO等[14]的研究都是通过二维的平面等效方式进行，将盘形滚刀破岩简化为侵入破岩过程，其研究成果表明将盘形滚刀破岩简化成二维侵入破岩的问题是可行的。基于此，本文主要研究盘形滚刀在推力作用下岩石内部裂纹的产生及扩展过程，将滚刀破岩问题简化为二维侵入问题。

滚刀破岩数值模型如图1所示，岩石的长×宽为300 mm×160 mm，根据滚刀刀圈的结构特性以及软件中刚性墙无法施加推力载荷的条件，在建模过程中滚刀采用球体clump模型代替。通过赋予滚刀clump单一恒定载荷和循环冲击动载荷等不同的推力载荷形式，盘形滚刀往下运动并逐步侵入岩石，模拟滚刀在不同载荷形式作用下的破岩形式，观察岩石内部裂纹萌发与扩展情况。其中滚刀冲击动载荷波形采取实验室常见的矩形波[15]，加载时间为24 μs。

图1 滚刀破岩数值模型

2 滚刀在不同恒定静载荷下破岩规律

2.1 滚刀在不同恒定静载荷下数值模拟

静载荷/ kN：(a) 20；(b) 26；(c) 32；(d) 38；(e) 44

从图2可见：当盘形滚刀以不同的静载荷侵入岩石中时，岩石内部同时存在剪切裂纹和张拉裂纹，整体表现为拉压复合破坏；当静载荷较小时(见图2(a))，盘形滚刀不能有效地侵入岩石，只能在岩石表面形成一些微小裂纹，甚至只发生弹性变形，破碎效果极差；当静载荷逐步增大时，岩石内部中间裂纹和侧向裂纹长度明显增大，破碎区域向岩石深部发展，侧向裂纹长度的增大速度高于中间裂纹长度的增大速度(见图2(b))；当静载荷增大到一定程度时(见图2(c))，岩石侧向裂纹往岩石自由平面发育，形成大体积破碎块，岩石破碎体积增到最大；当静载荷继续增大时，岩石内部的侧向裂纹与自由平面形成贯通，岩石破碎体积得不到明显增大，且滚刀下方发生过度破碎，消耗能量也过多，岩石破岩效果并不随之提高(见图2(d)和图2(e))。

盘形滚刀的破岩比能耗定义为刀具切削单位体积岩石所消耗的能量[17−18]，是表征破岩效率的重要参数，破岩比能耗越小，说明盘形滚刀破岩效率越高，其具体表达公式如下：

式中：为破岩比能耗；N为垂直力；为刀具破岩消耗的能量；为贯入度；为岩石破碎体积，=；为破碎面积之和，根据裂纹的扩展情况测量；为单位厚度。

在静载荷作用下，滚刀破岩裂纹长度、破碎体积、比能耗随静载荷变化关系如图3所示。从图3可见：当滚刀静载荷低于32 kN时，岩石内部产生的侧向裂纹长度与中间裂纹长度增长速度较大，裂纹分布的深度与其水平贯通面积也随之增大，破碎体积明显增大，滚刀破岩比能耗降低；当滚刀静载荷超过32 kN时，岩石内部裂纹长度增长不明显，破碎体积得不到明显增大，破岩比能耗变化不明显，反而有所上升，此时，静载荷增大值对岩石破碎效果影响不大；当静载荷为32 kN时，盘形滚刀比能耗最小，其值为9.33 MJ/m3，此时，盘形滚刀在静载荷作用下破岩效果最优。

(a) 静载荷与裂纹长度的关系；(b) 静载荷与比能耗和破碎体积的关系

2.2 滚刀在不同恒定静载荷下的实验研究

通过直线式盘形滚刀破岩实验台进行盘形滚刀破岩实验研究。实验装置由机架、水平工作台、液压系统和电控测试系统共4部分构成，整个实验台由液压系统进行驱动，盘形滚刀上下直线运动由垂直液压缸驱动，岩石纵向进给由纵向液压缸驱动。

实验时，将盘形滚刀安装于刀架上，并将盘形滚刀调至实验岩石正上方，通过垂直液压缸加载装置对滚刀施加垂直力，通过纵向液压缸控制工作台的前后移动，从而使得滚刀滚压切削岩石。实验滚刀使用常截面滚刀，直径为432 mm，刀刃宽为18 mm，刀刃角为20°。岩石力学参数如下：抗压强度为100.33 MPa，抗拉强度为5.69 MPa，弹性模量为11.45 GPa。由于实际的破岩总会出现岩石的阶跃式破坏，而滚刀上受到的力不会实现恒定，但通过设定实验台垂直油缸的油压推力使得整个过程滚刀受力在一定静载附近上下波动，近似为恒定载荷破岩。试验中，垂直油压分别选取6，7和8 MPa进行多组验证试验。

在静载荷作用下，滚刀破岩实验过程如下：首先，盘形滚刀在不同垂直载荷下侵入岩石；接着，控制实验台纵向油缸使得岩石向前运动而进行滚刀滚动切削实验。每次实验切削结束后，使用带百分表的游标卡尺测量滚刀侵入深度，量取不同点切削槽的宽度并取平均值，并测量统计破碎块的尺寸。使用摄像机观察记录滚刀侵入岩石时破碎坑的形状，统计滚刀侵入岩石破碎坑的体积。

在静载荷破岩试验中，在不同静载荷下，岩石破碎坑与破碎块的尺寸和形状均有所不同，滚刀的贯入度也不一样。在切削过程中，较大的静载荷能促进岩石裂纹扩展，使得中间裂纹以及侧向裂纹增长，从而导致岩石的破碎坑宽度增大，贯入度增大。所以，当静载荷增大时，岩石破碎坑增大，滚刀的贯入度也随之增大，被剥落的岩石碎屑增多。实验结果如表3 所示。

(2)With increasing number of the epochs,the errors in the carrier IAR decreased.

表3 不同的静载荷模型最终实验结果

从表3可见：当静载荷逐步增大时，滚刀的贯入度增大，岩石破碎坑体积与破碎坑的宽度也随之增大，但增长速度减缓，与模拟仿真变化趋势一致，验证了模拟仿真结果的可靠性。

3 滚刀在冲击动载荷下破岩规律

3.1 滚刀在冲击动载荷下受力规律

为了实现盘形滚刀静载荷和冲击载荷的衡量标准，使得滚刀加载静载荷与加载冲击动载荷消耗的能量相等，便于后续破碎效果比较，以能产生与静载荷作用时消耗能量相等的冲击载荷作为当量冲击载荷，并以此作为矩形波冲击载荷的峰值。产生此冲击载荷消耗的能量可由冲击杆动能推算得到。当滚刀分别在静载荷与矩形波冲击载荷作用下进行破岩时，通过观察比较静载荷与冲击动载荷的破岩情况，并计算各自的比能耗，比较两者的破岩效果。实验台的冲击加载设备简化图如图4所示。

图4 盘形滚刀冲击破岩受力示意图

滚刀与岩石相互作用下及滚刀在冲击动载荷作用下，其侵入微分方程的一般形式[19]为

式中：为冲击动载荷的侵入载荷；为侵入系数；为滚刀的平均波阻；()为滚刀冲击后承受的冲击载荷函数；为时间。在=0时，=0 N，解式(2)可得

考虑到冲击杆跟滚刀相互作用下，将冲击杆看成刚体，不考虑撞击面的变形，当初始条件为=0 s时，冲击杆速度=0，按照牛顿定律与一维应力波原理可得

式中：为冲击杆质量。将式(4)代入式(3)得

式中：=2/()；为撞击侵入指数，为量纲一的量。

可求得最大侵入力为

结合冲击破岩时消耗的动能为02/2，假定静载力破岩消耗的能量与冲击破岩消耗的能量一样，当量冲击载荷为最大侵入力的一半，则可得当量冲击载荷与静载荷作的功的关系如下：

3.2 滚刀在冲击动载荷下破岩规律

从图5可见当盘形滚刀以不同循环冲击载荷侵入岩石中时岩石内部的裂纹分布情况。对比于静载荷破岩情况，岩石内部滚刀下面的区域主要是剪切裂纹，以压破坏为主，而岩石内部的侧向裂纹主要由拉破坏所致；当冲击次数一样时，岩石的贯入度随着冲击动载荷的增大而增大，岩石内部产生的裂纹数目也随之增大，岩石内部的侧向裂纹得到扩展，并趋向于岩石的自由平面，有利于形成较大的破碎块，降低盘形滚刀破岩的比能耗，提高破岩效率。从图6可见：当岩石冲击动载荷峰值由264 kN变化到360 kN时，滚刀的贯入度由3.33 mm增大到4.21 mm，岩石内部侧向裂纹长度由39.55 mm增长到67.88 mm，岩石内部中间裂纹长度由53.48 mm增长到75.12 mm。观察图5(a)和图5(b)可见：在冲击载荷峰值的增量一样时，岩石内部侧向裂纹的扩展长度比中间裂纹扩展长度大。这是由于在盘形滚刀破岩过程中，冲击动载荷增大能促进岩石内部的侧向裂纹发育，导致岩石产生大体积破碎块，而岩石内部在滚刀贯入部位形成大面积破碎粉末，产生的中间裂纹不能得到有利发育。当单纯地提高冲击动载荷时(据图5(c)和图5(d))，岩石在高冲击动载荷的作用下，贯入度和破碎体积稍增大，但效果并不显著。从图5(a)也可看出：当冲击动载荷增大时，贯入度和破碎体积变化曲线的斜率变小，贯入度和破碎体积增大效果不明显。另外，对比图5(e)，(f)，(g)和(h)中盘形滚刀冲击动载荷破岩情形，当冲击载荷不变时，随着冲击次数增大，滚刀破岩各参数量变化趋势大致与增大冲击载荷的变化趋势一样，如图6所示。表4给出了各组冲击动载荷破岩模型的滚刀破岩比能耗。从表4可见：比能耗随着冲击动载荷的增大先减少再增大。而当冲击动载荷施加的次数增大时，岩石在高冲击动载荷的作用下，其内部已经形成过破碎，从而导致岩石反复破碎，消耗的能量也会过多，容易导致能量耗散，因此，冲击动载荷冲击次数对于破岩效果提高影响不大，比能耗反而增大。

(a) P冲=264 kN (n=4)；(b) P冲=312 kN (n=4)；(c) P冲=336 kN (n=4)；(d) P冲=360 kN (n=4)；(e) n=2 (P冲=312 kN)；(f) n=4 (P冲=312 kN)；(g) n=6 (P冲=312 kN)；(h) n=8 (P冲=312 kN)

(a) 冲击载荷与破碎体积跟贯入度的关系；(b) 冲击载荷与裂纹长度的关系；(c) 冲击次数与破碎体积跟贯入度的关系；(d) 冲击次数与裂纹长度的关系

表4 不同的冲击动载荷模型最终比能耗

4 静载荷与冲击动载荷破岩效果比较

冲击作为一种及其简单的破岩手段，相对于静载荷，其能在较短时间获得很大的力，能够使岩石内部瞬间萌发大量裂纹，为后续破岩打下了有利基础。在冲击动载荷作用下，岩石的侵入硬度和强度都有所提高，滚刀破岩比能耗相对于静载荷作用较高。BAKER等[20−21]通过对玻璃、瓷器和水泥砂浆试块进行强度测试试验，发现抗压强度和抗拉强度的倒数与加载时间的对数呈线性关系；随着加载时间减少，物体强度随之增大，这对滚刀破岩有利。在滚刀破岩过程中，分别比较在静载荷为26，32，38和44 kN，及相对应的当量冲击动载荷分别264，312，336和360 kN作用下的4组硬岩破岩比能耗，结果见图7。

1—静载荷；2—动载荷。

从图7可见：对于此种硬岩，滚刀在动、静载荷作用下比能耗的整体变化呈下降趋势；滚刀破岩的比能耗都随着静载荷或动载荷增大而减低，变化趋势近似一致；纯冲击动载荷破岩的比能耗都高于静载荷作用下的比能耗，相对应动静载荷比能耗的比值均值约为1.4，单纯的冲击动载荷并不能有效地提高破岩效率。

5 结论

1) 随着静载荷增大，岩石破碎体积和侧向裂纹长度先增大后趋于不变，破岩比能耗先减少后有所上升，当静载荷为32 kN时破岩效果最优。

2) 当静载荷逐步增大时，滚刀贯入增大，岩石破碎块体积与破碎坑的宽度也随之增大，但增长速度减缓，与模拟仿真变化趋势一致。

3) 在矩形波冲击动载荷作用下，岩石裂纹扩展情况与静载荷的扩展情况相似。当峰值及施加次数增大时，滚刀贯入度随之增大，裂纹长度增大且有向水平贯穿的趋势，岩石破碎体积增大，破岩比能耗减少。单纯靠提高冲击载荷或冲击次数不能显著提高破岩效率。

4) 滚刀在静载荷和冲击动载荷作用下，比能耗的变化趋势基本一致，但冲击动载荷破岩的比能耗比静载荷作用下的高，大约是静载荷破岩的1.4倍，故单纯的冲击动载荷并不能有效提高破岩效率。

[1] LIU H Y, KOU S Q, LINDQVIST P A, et al. Numerical simulation of the rock fragmentation process induced by indenters[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(4): 491−505.

[2] 刘建琴, 刘蒙蒙, 郭伟. 硬岩掘进机盘型滚刀回转破岩仿真研究[J]. 机械工程学报, 2015, 51(9): 199−205. LIU Jianqin, LIU Mengmeng, GUO Wei. Research on the simulation of cutting rock rotary by hard rock tunnel boring machine disc cutters[J]. Journal of Mechanical Engineering, 2015, 51(9): 199−205.

[3] 夏毅敏, 薛静, 周喜温. 盾构刀具破岩过程及其切削特性[J]. 中南大学学报(自然科学版), 2011, 42(4): 954−959. XIA Yimin, XUE Jing, ZHOU Xiwen. Rock fragmentation process and cutting characteristics on shield cutter[J]. Journal of Central South University (Science and Technology), 2011, 42(4): 954−959.

[4] 谭青, 徐孜军, 夏毅敏, 等. 2种切削顺序下TBM刀具破岩机理的数值研究[J]. 中南大学学报(自然科学版), 2012, 43(3): 940−946. TAN Qing, XU Zijun, XIA Yimin, et al. Numerical study on mode of breaking rock by TBM cutter in two cutting orders[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 940−946.

[5] MOON T, OH J. A Study of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J]. Rock Mechanics and Rock Engineering, 2012, 45(5): 837−849.

[6] 杨岳峰, 梁正召, 唐春安. 冲击作用下的压头破岩机制研究[J]. 岩土力学, 2013, 34(6): 1775−1785. YANG Yuefeng, LIANG Zhengzhao, TANG Chunan. Rock fragmentation mechanism induced by a drill bit subjected to dynamic loading[J]. Rock and Soil Mechanics, 2013, 34(6): 1775−1785.

[7] HUO Junzhou, SUN Xiaolong, LI Guangqing, et al. Multi-degree-of-freedom coupling dynamic characteristic of TBM disc cutter under shock excitation[J]. Journal of Central South University, 2015, 22(9): 3326−3337.

[8] 霍军周, 欧阳湘宇, 王亚杰, 等. 重载冲击激励下TBM刀盘振动特性的影响因素分析[J]. 哈尔滨工程大学学报, 2015, 36(4): 555−559. HUO Junzhou, OUYANG Xiangyu, WANG Yajie, et al. Analysis of influencing factors of vibration behaviors of TBM cutterhead under heavy impact loads[J]. Journal of Harbin Engineering University, 2015, 36(4): 555−559.

[9] 金解放, 李夕兵, 殷志强, 等. 轴压和循环冲击次数对砂岩动态力学特性的影响[J]. 煤炭学报, 2012, 37(6): 923−930. JIN Jiefang, LI Xibing, YIN Zhiqiang, et al. Effects of axial pressure and number of cyclic impacts on dynamic mechanical characteristics of sandstone [J]. Journal of China Coal Society, 2012, 37(6): 923−930.

[10] 赵伏军, 李夕兵, 冯涛, 等. 动静载荷耦合作用下岩石破碎理论分析及试验研究[J]. 岩石力学与工程学报, 2005, 24(8): 1315−1320. ZHAO Fujun, LI Xibing, FENG Tao, et al. Theoretical analysis and experiments of rock fragmentation under coupling dynamic and static loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1315−1320.

[11] 谭青, 张旭辉, 夏毅敏, 等. 不同围压与节理特征下盘形滚刀破岩数值研究[J]. 煤炭学报, 2014, 39(7): 1220−1228. TAN Qing, ZHANG Xuhui, XIA Yimin, et al. Numerical study on breaking rock by disc cutter at different confining pressure and joint characteristics case[J]. Journal of China Coal Society, 2014, 39(7): 1220−1228.

[12] MOON T, NAKAGAWA M, BERGER J. Measurement of fracture toughness using the distinct element method[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 449−456.

[13] 刘建琴, 刘蒙蒙, 郭伟, 等. 隧道掘进机刀盘结构性能评价研究关键问题分析[J]. 现代隧道技术, 2014, 51(2): 5−10. LIU Jianqin, LIU Mengmeng, GUO Wei, et al. Analysis of key problems in the structural performance evaluation for TBM cutter heads[J]. Modern Tunnelling Technology, 2014, 51(2): 5−10.

[14] INNAURATO N, OGGERI C, ORESTE P P, et al. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J]. Rock Mechanics and Rock Engineering, 2007, 40(5): 429−451.

[15] 廖志毅, 梁正召, 唐春安, 等. 动静组合作用下刀具破岩机制数值分析[J]. 岩土力学, 2013, 34(9): 2682−2689, 2698. LIAO Zhiyi, LIANG Zhengzhao, TANG Chunan, et al. Numerical simulation of rock fracture mechanism induced by a drill bit under combined dynamic and static loading[J]. Rock and Soil Mechanics, 2013, 34(9): 2682−2689, 2698.

[16] 张旭辉. 围压与节理作用下滚刀破岩特性研究[D]. 长沙: 中南大学机电工程学院, 2015: 64−76. ZHANG Xuhui. The study of rock breaking characteristic by disc cutters under confining pressure and joint[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2015: 64−76.

[17] 茅承觉, 刘友元. 隧洞掘进机盘形滚刀滚压岩石的试验[J]. 工程机械, 1985(3): 21−26. MAO Chengjue, LIU Youyuan. Test on rolling rock by disc cutter of tunnel boring machine[J]. Construction Machinery and Equipment, 1985(3): 21−26.

[18] 霍军周, 杨静, 孙伟, 等. 不同模式下TBM刀群三维回转切削仿真与优化设计[J]. 哈尔滨工程大学学报, 2014, 35(11): 1403−1408. HUO Junzhou, YANG Jing, SUN Wei, et al. Simulation and optimization design of three-dimensional rotating cutting action of TBM cutter group with different modes[J]. Journal of Harbin Engineering University, 2014, 35(11): 1403−1408.

[19] 徐小荷, 余静. 岩石破碎学[M]. 北京: 煤炭工业出版社, 1984: 159−180. XU Xiaohe, YU Jing. Rock crushing study[M]. Beijing: China Coal Industry Press, 1984: 159−180.

[20] BAKER T C, PRESTON F W. Fatigue of glass under static loads[J]. Journal of Applied Physics, 1946, 17(3): 170−178.

[21] 铃木光. 岩体力学与测定[M]. 北京: 煤炭工业出版社, 1980: 110−146. LIN Muguang. Rock mechanics and measurement[M]. Beijing: China Coal Industry Press, 1980: 110−146.

(编辑 陈灿华)

Disc cutter cutting mechanism under static loading and impact dynamic loading conditions

TAN Qing1, 2, LAO Tongbing1, 2, ZHANG Guiju1, 2, 3, ZHANG Xuhui1, 2, YI Liang1, 2, XU Shunsheng4

(1. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;3. Department of Mechanical and Energy Engineering, Shaoyang University, Shaoyang 422004, China;4. School of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China)

In order to research the disc cutter cutting mechanism under static loading and impact dynamic loading conditions, a two-dimensional numerical simulation method with which disc cutters break rock was established based on the particle discrete element method. Stress boundary condition was considered instead of velocity boundary condition. The dynamic process of breaking rock under constant static loading and impact dynamic loading was analyzed. The effects of load and impact cycle numbers on the characteristics of breaking rock were studied. Finally, an experiment was carried out on the linear experiment platform. The results show that the increase of static load can improve the rock fragmentation effects under constant static loading. When static load reaches a certain value, the rock fragmentation effects change inconspicuously and there is a optimal value which makes the rock fragmentation effects best. Under impact dynamic loading, the rock crack propagation behavior is similar to that under static loading, but the rock is prior to shear failure. With the increase of dynamic load and frequency, the number of rock cracks increases and the specific energy consumption decreases and then changes little. Meanwhile, the rock cracks tend to penetrate rock free surface. The variation trend of the specific energy consumption under constant static loading is consistent with that under cyclic impact dynamic loading and the former is 1.4 times of the latter.

cutter; particle flow; cutting characteristics; specific energy consumption; constant static loading; impact dynamic loading

TP391.9；U455.3+1

A

1672−7207(2018)01−0101−08

10.11817/j.issn.1672-7207.2018.01.014

2017−01−02；

2017−03−14

国家重点基础研究发展计划(973计划)项目(2013CB035401)；国家高技术研究发展计划(863计划)项目(2012AA041801)；国家自然科学基金资助项目(51274252) (Project(2013CB035401) supported by the National Basic Research Development Program(973 Program) of China; Project(2012AA041801) supported by the National High Technology Research and Development Program(863 Program) of China; Project(51274252) supported by the National Natural Science Foundation of China)

张桂菊，博士研究生，副教授，从事岩石切削机理研究；E-mail: zhangguiju1999@sina.cn