Multi-scale thermodynamic analysis method for 2D SiC/SiC composite turbine guide vanes

Xin LIU,Xiuli SHEN,*,Longdong GONG,Peng LI

aSchool of Energy and Power Engineering,Beihang University,Beijing 100083,China

bNavigation and Control Technology Research Institute of China Ordnance Industries,Beijing 100089,China

1.Introduction

The high-temperature resistance of hot aero engine components,such as the guide vane of a high-pressure turbine,has increased with the growth of the thrust–weight ratio.The turbine inlet temperature of an aero engine with a thrust–weight ratio of 15:20 reaches 1900–2100 °C.1Under the consideration of blade cooling and thermal barrier coating,high-pressure turbine guide vanes need to resist temperatures exceeding 1300°C.2The SiC/SiC Ceramic Matrix Composite(CMC)possesses high-temperature resistance(can resist temperature reaching 1450°C1),corrosion resistance,and low density.As the result,this material not only meets the temperature requirements of the high-pressure turbine guide vane but also increases the thrust–weight ratio by reducing the weight of the guide vane.

Present studies on CMC turbine guide vanes are mainly based on experiments and macroscopic numerical simulations.Brewer et al.calculated the macroscopic stress distribution of a 2D woven CMC turbine guide vane through a numerical simulation and indicated that the maximum stress occurred on the trailing edge.3Verrilli et al.conducted a thermal shock test of a 2D woven SiC/SiC-CMC turbine guide vane processed by Chemical Vapor Infiltration(CVI).The temperature field and the macroscopic stress distribution of the vane were simulated in the given test condition with the conclusion that high stress distribution appeared at the leading edge.4

Homogenized stress and strainfields are generally obtained from the Finite Element Method(FEM)in the macroscopic numerical simulation of CMC turbine guide vanes to conduct strength evaluation.Given that woven CMC exhibits inhomogeneity at the microscopic scale,the microscopic stress distribution cannot be reflected by the homogenized macroscopic stressfield.5Since there are differences between the mechanical properties of the compositefiber and matrix,it is necessary to obtain the stress distribution of thefiber and matrix separately by microscopic analysis.Afterward,accurate judgments can be made about turbine guide vane failure.Although the experimental method can be adopted to obtain the macroscopic failure criterion of a certain CMC turbine guide vane,the mechanical properties of the material can change with differentfiber volume fraction,braided structure,porosity and so on.This fact leads to the change in the failure criterion of CMC turbine guide vanes at the macroscopic scale.Considering the high cost and complexity of CMC turbine guide vane experimentation,the test method is generally adopted forfinal verification.However,the mechanical properties of the fiber and matrix do not change with the structural characteristics of the material,and the micro-analysis method can be applied to CMC turbine guide vanes with different materials and processes.

Complete material thermodynamic properties are the basis of the numerical simulation of CMC turbine guide vanes.The in-plane mechanical properties of 2D woven CMC can be measured through an experiment,but the out-plane normal mechanical properties can only be obtained through numerical analysis at present.6The structure of a CMC turbine guide vane processed by CVI is complex,and the influence of periodic structure modeling,matrix porosity,and thermal–mechanical load should be considered in performance prediction.7Therefore,it is essential to generate a method to predict the thermodynamic properties of CVI-processed 2D woven CMC.

In the 1970s,Lions8and Kesavan9,10proposed the multiscale method based on homogenization theory.Cun and Cao proved that this method converges to the real solution in mathematics.11Hassani and Hinton introduced the multi-scale asymptotic analysis method.12–14Multi-scale asymptotic homogenization has become an important method to analyze periodic composite structures.Prediction of the thermodynamic properties of woven CMC and multi-scale stress and strain analysis of CMC turbine guide vanes can be conducted with this method.Barroqueiro et al.studied the actual use of the multi-scale homogenization method in calculation software.The thermodynamic properties and stress distribution of a micro Representative Volume Element(RVE)for both unidirectionalfiber-reinforced composite and standard tensile test specimen were predicted as examples.15Gong and Shen established the multi-scale thermal–mechanicalcoupling method and conducted numerical simulation of a unidirectionalfiber-reinforced composite.The calculation results of the material parameters were in good agreement with the experimental results.16This work serves as a theoretical basis for the application of the multi-scale homogenization method in 2D woven CMC turbine guide vanes.

Overall,the previous work cannot meet the demand for the prediction of the thermodynamic properties of 2D SiC/SiCCMC and the multi-scale stress and strain analysis of CMC turbine vanes.Firstly,the research of 2D woven composites is mainly based on void free RVE model.17,18However,the microstructure of CVI SiC/SiC-CMC is complex with a large number of voids which influence the material property.19A reasonable and effective RVE model fully considering void structure is needed.Secondly,the numerical simulation of the CMC turbine guide blade stays at the macro level without considering the inhomogeneous distribution of the micro stress.There is no method of calculating the distribution of micro stress from the macroscopic response of the CMC turbine vane.It is not conducive to judging the failure of guide vanes accurately and making full use of the designable advantage.Some researchers have been carried out aiming at the above problems in this paper.

This study investigated the multi-scale thermodynamic analysis method.Initially,a 2D woven composite RVE model with porosity was established based on the minimum energy principle20to predict the thermodynamic properties of CVI-processed 2D woven SiC/SiC-CMC.Moreover,the macroscopic response of the vane under given conditions was predicted with the material distribution model according to the processing technology of the 2D woven SiC/SiC-CMC turbine guide vane.Finally,the stress distribution of the micro-scale RVE model was simulated,and the microscopic stress distribution characteristics were analyzed.Strictly,a complete and feasible multi-scale thermodynamic analysis method was established for SiC/SiC-CMC turbine guide vanes.The predicted material properties and the macroscopic response of the turbine guide vane were in good agreement with the experimental results.

2.Multi-scale thermal–mechanical coupling method and finite element implementation

2.1.Mathematical derivation

The linear thermal–mechanical problem is provided as

where σ,λ,andtare the component of stress tensors,thermal conductivity,and temperature,respectively;iandjrepresent 3 orthogonal directions;f is the load per unit volume;ψ represents the heat generated by the inner source per unit volume in unit time;xiis the coordinate in different directions.

On account of the similar forms of mechanical equilibrium and heat conduction differential equations,extended differential operator matrix and combinedfield quantity are introduced.Then,Eq.(1)can be written in a unified form as

where L is the differential operator matrix,C is the extended matrix of stiffness and thermal conductivity coefficient,U is the combinedfield of displacement and temperature,A is the thermal expansion coefficient matrix,and F is the combinedfield of external loads and internal heat source.

As shown in Fig.1,for periodic composites,the macro displacement vector is a function of not only macro coordinate x but also micro coordinate y.Define a small parameter ε(0 ＜ ε＜1)as the ratio of the actual length of a unit vector in the micro coordinates to the realistic length of a unit vector in the macro coordinates,and y=x/ε.Therefore,any field vector φεhas the following form:

whereYis the micro period andn=0,1,2,....

The small parameter asymptotic expansion of U in Eq.(2)is

Through asymptotic expansion derivation,we conclude that the generalized equilibrium equations are

The macroscopic homogenization matrix of stiffness and thermal conductivity coefficient CUis

where Ω is the integral variable.

The macroscopic homogenization matrix of the thermal expansion coefficient AUis

The relationship between micro stress σεand macroscopic physical quantities is expressed as

whereVis the micro cell volume,M（y）and P（y）are coefficient matrices related to micro coordinate y,and U0is the macrofield of displacement and temperature.

2.2.Finite element solution of macro thermodynamic properties

By introducing shape function N,thefinite element solution of M（y）and P（y）can be written as

where q and q*can be obtained by the following equations:

Fig.1 Periodic structural unit of composites.

where q and q*are the extended displacement vectors of the nodes,B=LN is the extended strain matrix,and J is the Jacobian matrix,ξ,η,ζ are the integral variable.

We conclude that

The elastic modulus,Poisson’s ratio,thermal conductivity,and thermal expansion coefficient are easily obtained from CUand AU.

2.3.Finite element solution of micro stress distribution

From Eqs.(8)–(10),the expression of micro stress σεcan be derived as

Eq.(15)shows the relationship between micro stress distribution and macro physical quantities.q and q*are viewed as microscopicfluctuations caused by the distribution of material properties.Lyi（Nq*）U0in Eq.(15)contains the micro temperaturefluctuation caused by the thermal conductivity coefficient distribution.This part represents the effect of micro temperaturefluctuation on micro stress distribution.

According to this derivation,a multi-scale thermodynamic analysis program was developed in VC++6.0.This program can calculate the thermodynamic properties of the materials and the stress distribution of the micro-scale RVE model.

3.Prediction of thermodynamic properties of SiC/SiC-CMC

3.1.RVE model offiber bundle and 2D woven CMC

The microstructure of thefiber bundle obtained with a Scanning Electron Microscope(SEM)is shown in Fig.2.

Thefiber volume fraction of thefiber bundle was 89.3%,as measured from the SEM microstructure photographs.The RVE model of thefiber bundle was established(shown in Fig.3)according to this.The effect of the pore on thefiber bundle was disregarded because of the negligible amount.

The micro structure of the 2D woven CVI-processed SiC/SiC-CMC is illustrated in Fig.4.

The characteristics of the microstructure of CVI-processed woven CMC can be concluded from the SEM images as follows.First,the preform is uniformly distributed.Thefiber bundle is connected by the matrix with a consistent crosssectional shape.Second,the matrix thicknesses in each direction along the surface of thefiber bundles are the same,and each layer is closed by the connection matrix along the thickness direction after deposition.Third,the pores are periodically distributed in the matrix and the position and shape are basically similar.

The structural parameters were obtained from the data collected from SEM images of different parts of the material with statistical analysis.According to the modeling method provided by Ref.20,the RVE model of 2D woven composites in consideration of porosity was established as Fig.5.To reveal the internal structure of the RVE model,the layer was adjusted to become transparent.The model illustrates the internal structure of 2D woven composites ideally,and the effect of porosity is fully considered.

3.2.Thermodynamic performance calculation and experimental verification

Thermodynamic parameters of SiCfiber and SiC matrix are the basis of CMC performance prediction.The material supply unit only provided the thermal expansion coefficient of the SiC matrix,and the existing researches focus on the mechanical properties or thermal conductivity,but cannot provide the complete original parameters.Therefore,through the analysis of the parameters of thefiber and the matrix material provided by a number of literatures,the thermodynamic parameters of the SiC-matrix and SiC-fiber are listed in Table 1.

The calculated thermodynamic properties of thefiber bundles are shown in Table 2,whereEis the modulus of elasticity,Gis the shear modulus,μ is the Poisson ratio,and α is the coef-ficient of thermal expansion.The multi-scale thermodynamic analysis method and the RVE model of thefiber bundle were used to calculate.Subscripts 1 and 2 represent the transverse directions of thefiber bundle,and subscript 3 represents the longitudinal direction.The equivalent performance parameters offiber bundles are orthotropic.

Based on the thermodynamic properties of thefiber bundle and matrix,the properties of 2D woven SiC/SiC-CMC were predicted with the multi-scale thermodynamic analysis method and the RVE model.The result is shown in Table 3.Subscripts 1 and 2 represent the in-plane warp and weft directions,and subscript 3 represents the out-plane normal direction.The performance parameters of the material are orthotropic.

To verify the accuracy of the prediction results,a uniaxial tensile test was conducted on 2D woven SiC/SiC-CMC.A comparison of the test and predicted results(Table 4)shows that the relative error is 4.18%,which means that the calculated material performance parameters can be used to analyze the thermodynamic response of CMC turbine guide vanes at micro and macro scales.

Fig.2 Micro structure offiber bundle.

Fig.3 RVE model offiber bundle.

Fig.4 Micro structure of 2D woven CVI-processed SiC/SiCCMC.

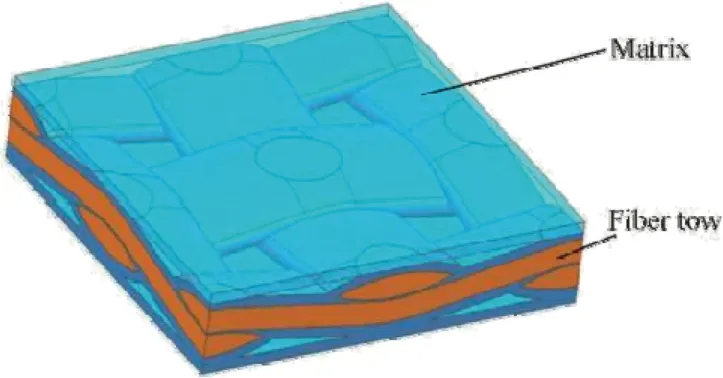
Fig.5 RVE model of 2D woven composites with porosity.

4.Thermodynamic response analysis of a CMC turbine guide vane in multiple scales

4.1.Thermal deformation test of CMC turbine vane

To acquire the temperaturefield and validate the guide vane analysis method,a static experiment was conducted on a CMC turbine guide vane.Strain distribution was observed with a temperature difference of more than 150°C at the trailing edge.To facilitate strain measurement,the hightemperature resistant metal part is open at the end,as shown in Fig.6.

Eleven temperature control points were arranged on the CMC turbine guide vane,as shown in Fig.7.The change in temperature at each point was measured by a thermocouple.The output power of the high-frequency induction furnace was kept stable when the temperature difference between points 2 and 10 exceeded 150°C.The temperature at each point is listed in Table 5.

As shown in Fig.8,thefirst principal strain at the trailing edge was measured with a VIC-3D HSt full-field strain measurement system.Points P0,P1,and P2 were selected randomly in the test section;the strain values are 2.935×10-3,2.777×10-3,and 2.211×10-3,respectively.The average value of thefirst principal strain in the test section is 2.913×10-3(C0).

Table 1 Thermodynamic properties of component materials.

Table 2 Thermodynamic properties offiber bundle.

Table 3 Thermodynamic properties of 2D woven SiC/SiC-CMC.

Table 4 Comparison of calculated and experimental values of material properties.

Fig.6 Heating device of experiment.

Fig.7 Distribution of temperature control points.

4.2.Macro mechanical response calculation

Thefinite element model of the CMC turbine guide vane is shown in Fig.9.The macroscopic equivalent thermodynamic properties of 2D woven SiC/SiC-CMC were predicted.

The property distribution model of the material was established according to the manufacturing process of the CMC turbine guide vane.When the vane was processed,the SiCfiber cloth was wrapped on an inner cavity mold initially.Then,the blank was deposited through CVI.Finally,the CMC turbine guide vane was obtained by mechanical processing.In this manufacturing process,although the local coordinate system of the 2D woven CMC turbine guide vane changed with the shape of the component,the material properties were kept continuous.Thus,the material principal axis was determined by the woven structure and shape of the curved surface.The material distribution model involved two aspects.First,the in-plane warp or weft direction offiber bundle was regarded as thefirst principal axis direction.Second,the local normal direction of the turbine guide vane surface was regarded as the third principal axis direction.The second principal axis direction was determined by the right-hand rule.After mapping the material distribution to thefinite element model of the turbine guide vane,the local model was showed with the enlarged material distribution coordinate of the local unit as Fig.10.

The location and temperature of the 11 controlling points are shown in Fig.7 and Table 5.The convective heat transfer coefficient on the inner wall of the turbine guide vane is 10 W/(m2·°C).The atmospheric temperature is 25 °C.Temperature distribution was obtained through thermal–mechanical coupling analysis,as shown in Fig.11.To simulate the boundary condition in the test state,axial and circumferential displacement constraints were imposed on the sixth controlling point and a radial displacement constraint was imposed on the upper cross section of the turbine guide vane.

Thefirst principal strain distribution of the vane obtained from the macro analysis is shown in Fig.12 and the trailing edge is enlarged in Fig.13.The maximum and minimumfirst principal strains are 2.774×10-3and 2.574×10-3,respectively.The average value of thefirst principal strain at the trailing edge is 2.650×10-3.Table 6 provides a comparison of the analysis and experimental results.The relative error is 9.7%.

Fig.8 First principal strain distribution at trailing edge of CMC guide vane.

Fig.9 Finite element model of CMC turbine guide vane.

Fig.11 Distribution of temperature on guide vane.

Fig.12 First principal strain distribution of guide vane.

Fig.10 Local model of material coordinate mapping.

Fig.13 First principal strain distribution of guide vane on trailing edge.

Table 6 Comparison of calculated and experimental values of thefirst principal strain.

4.3.Simulation of micro stress distribution

The equivalent stress distribution of the vane is shown in Fig.14.The maximum equivalent stress is located at node 3256 near the trailing edge of the guide vane.The local coordinate system number of this node is 1251.Different from the turbine guide vane of isotropic metal materials,that of the composite material is orthotropic.The properties in normal and in-plane directions are different.Thus,interlaminar and in-plane stress should be discussed separately.

The macro stress distribution of the trailing edge in local coordinate system 1251 is shown in Fig.15.According to the processing characteristics of the CMC turbine guide vane,the warp or weft direction of thefiber bundle represents the in-plane stress level(stress-Xin Figs.15 and 16).The normal direction of the blade curved surface represents the interlaminar stress level(stress-Yin Figs.15 and 16).

The macro strain,displacement,and temperature of node 3256 were inputted to the microfluctuating matrix to calculate the stress parameters of the nodes attached to the micro RVE model.The micro stress distribution of the 2D woven RVE model simulated with Tecplot software is shown in Fig.16.The macro stress and the maximum value of micro stress distribution of node 3256 are summarized in Table 7.In both directions,the maximum value of micro stress distribution is more than 1.5 times larger than that of macro stress distribution.

Fig.14 Distribution of equivalent stress.

Fig.15 Macroscopic stress distribution of trailing edge in local coordinate system.

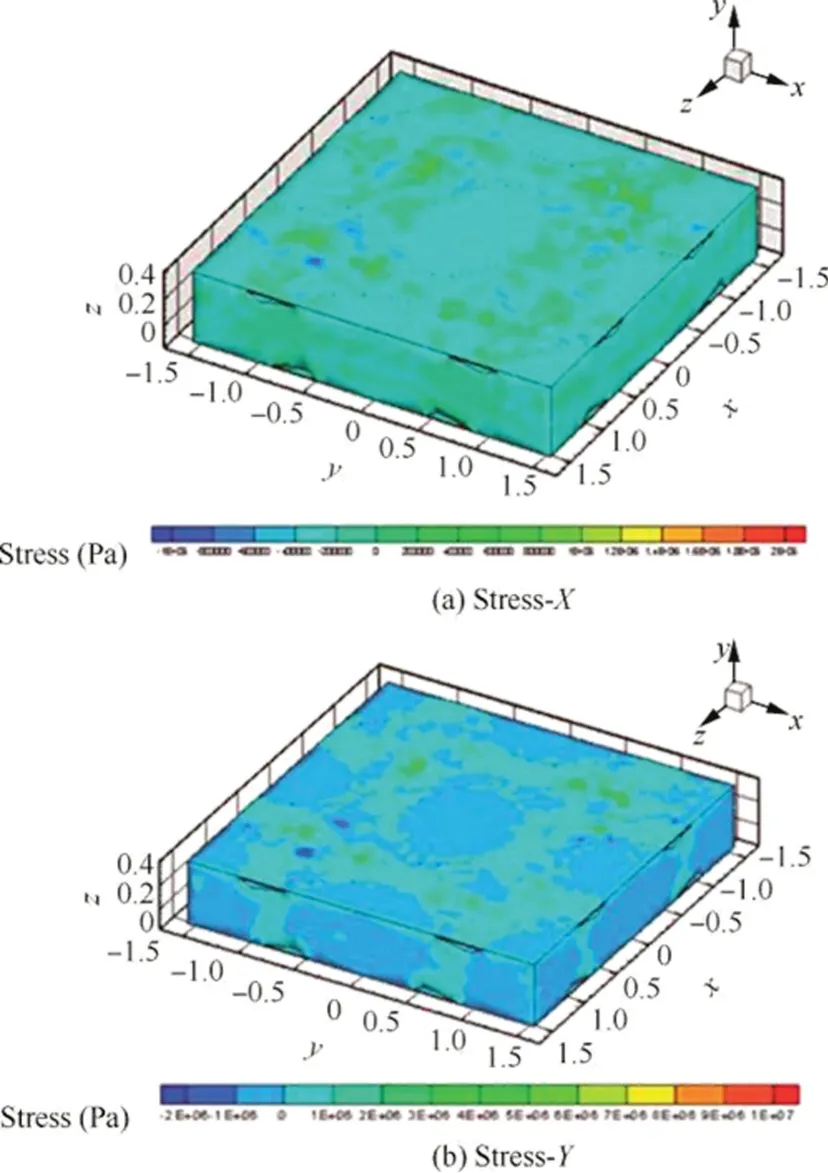
Fig.16 Microscopic stress distribution of RVE model.

Table 7 Comparison of macroscopic and maximum microscopic stresses.

Fig.17 Locations and numbers of nodes.

To verify the universality of the results,the macro stress and the maximum value of micro stress distribution of several other nodes in local coordinate systems were calculated.The positions and numbers of the points are shown in Fig.17.The calculation results are compared in Table 8.The maximum value of micro stress distribution is larger than that of macro stress at different positions on the turbine guide vane.The vane could be destroyed because the stress at the microscopic scale is too large before macro strength reaches its limitation.Therefore,the influence of micro stress distribution should be considered when the stress and strain of CMC turbine guide vanes are analyzed through a numerical method.

Fig.18 shows the cross-section where the micro stress of node 3256 is maximum in the interlaminar normal direction.The maximum value is on the upper surface,which can be considered as an interlayer matrix of CMC.The characteristic of stress distribution is consistent with the delamination failure of the 2D woven composites.As shown in Fig.19,the distribution of high stress on the cross section is consistent with the location of the pores in the RVE model.Stress increases with the rise of the pore volume and reaches the maximum value at the connections ofA,B,C,andD.We assume that the high stress distribution in the interlayer matrix is due to the porosity in the composites and the stress in the interlayer matrix increases with the increase in pore volume.The relevant laws require further study.

Table 8 Comparison of macroscopic and maximum microscopic stresses of nodes.

Fig.18 Section of maximum stress in inter laminar normal direction.

5.Conclusions

(1)The multi-scale thermodynamic analysis method of the CMC turbine vane was investigated in this paper.The thermodynamic properties of CVI-processed SiC/SiC-CMC were predicted with an RVE model with porosity.The relative error between the calculated and experimental in-plane tensile moduli is 4.2%.The analysis method is accurate and effective,which can provide complete data for component analysis.A macroscopic numerical simulation and an experiment were conducted on the CMC turbine guide vane under given conditions.The relative error between the predicted strain on the trailing edge and the experimental value is 9.7%.

Fig.19 Comparison of pore and stress distributions.

(2)The micro stress distribution of the CMC turbine guide vane was simulated.The maximum value of micro stress is larger than that of macro stress.Thus,the influence of micro distribution should be considered when the stress and strain of CMC turbine guide vanes are analyzed through a numerical method.The maximum value of stress in the interlaminar normal direction is located in the interlayer matrix.The high stress distribution of the interlayer matrix is due to the porosity in the composites.The stress in the interlayer matrix increases with the rise of the pore volume.

1.Wen SQ,He AJ.Application of CMC on thermal parts of aeroengine.J Aeronaut Manuf Technol2009;(Z):4–7[Chinese].

2.Vedula V,Shi J,Jarmon D,Zadrozny G.Ceramic matrix composite turbine vanes for gas turbine engines.ASME turbo expo:power for land,sea,and air;2005 June 6–9;Reno,USA.New York:ASME;2005.p.247–51.

3.Brewer D,Verrilli M,Calomino A.Ceramic matrix composite vane subelement burst testing.ASME turbo expo:power for land,sea,and air;2006 May 8–11;Barcelona,Spain.New York:ASME;2006.p.279–84.

4.Verrilli M,Calomino A,Robinson RC,Thomas DJ.Ceramic matrix composite vane subelement testing in a gas turbine environment.In:ASME turbo expo:power for land,sea,and air;2004 June 14–17;Vienna,Austria.New York:ASME;2004.p.393–9.

5.Dong JW,Sun LG,Hong P.Homogenization-based method for simulating micro-stress of 3D braided composites.J Acta Materiae Compositae Sinica2005;22(6):801–5[Chinese].

6.Murthy PLN,Nemeth NN,Brewer DN,Mital S.Probabilistic analysis of a SiC/SiC ceramic matrix composite turbine vane.J Compos Part B Eng2008;39(4):694–703.

7.Li J,Jiao GQ,Wang B,Li L,Yang CP.Damage characteristics and constitutive modeling of the 2D C/SiC composite:Part I–Experiment and analysis.Chinese J Aeronaut2014;27(6):1586–97.

8.Lions JL.Some methods in the mathematical analysis of systems and their control.Beijing:Science Press;1981.

9.Kesavan S.Homogenization of elliptic eigenvalue problem I.J Appl Math Optim1979;5(1):153–67.

10.Kesavan S.Homogenization of elliptic eigenvalue problem II.J Appl Math Optim1979;5(1):197–216.

11.Cun JZ,Cao LQ.Finite element method based on two scale asymptotic analysis.J Mathematica Numerica Sinica1998;20(1):89–102[Chinese].

12.Hassani B,Hinton E.A review of homogenization and topology optimization I-Homogenization theory for media with periodic structure.J Comput Struct1998;69(6):707–17.

13.Hassani B,Hinton E.A review of homogenization and topology optimization II-Analytical and numerical solution of homogenization equations.J Comput Struct1998;69(6):719–38.

14.Hassani B,Hinton E.A review of homogenization and topology optimization III-Topology optimization using optimality criteria.J Comput Struct1998;69(6):739–56.

15.Barroqueiro B,Dias-de-Oliveira J,Pinho-da-Cruz J,Andrade-Campos A.Practical implementation of asymptotic expansion homogenisation in thermoelasticity using a commercial simulation software.J Compos Struct2016;141:117–31.

16.Gong LD,Shen XL.Thermal-elastic two-scale asymptotic analysis method for micro periodic composites and implementation utilizing finite element method.J Propuls Technol2016;37(1):18–24[Chinese].

17.Bakar IAA,Kramer O,Bordas S,Rabczuk T.Optimization of elastic properties and weaving patterns of woven composites.J Compos Struct2013;100(5):575–91.

18.Obert E,Daghia F,Ladeve`ze P,Ballere L.Micro and meso modeling of woven composites:transverse cracking kinetics and homogenization.J Compos Struct2014;117:212–21.

19.Chateau C,Ge´le´bart L,Bornert M,Cre´pin J.Micromechanical modeling of the elastic behavior of unidirectional CVI SiC/SiC composites.J Int J Solids Struct2015;58(1):322–34.

20.Shen XL,Gong LD.Numerical modeling of braided composites using energy method.ASME international mechanical engineering congress and exposition;2014 November 14–20;Montreal,Canada.New York:ASME;2014.p.1–6.

21.Lamon J,Thommeret B,Percevault C.Probabilistic-statistical approach to matrix damage and stress-strain behavior of 2-D woven SiC/SiC ceramic matrix composites.J Eur Ceram Soc1998;18(13):1797–808.

22.Katoh Y,Ozawa K,Shih C,Nozawa T,Shinavski RJ,Hasegawa A,et al.Continuous SiCfiber,CVI SiC matrix composites for nuclear applications:Properties and irradiation effects.J Nucl Mater2014;448(1–3):448–76.

23.Youngblood GE,Senor DJ,Jones RH,Graham S.The transverse thermal conductivity of 2D-SiCf/SiC composites.J Compos Sci Technol2002;62(9):1127–39.