High-speed unsteadyflows past two-body configurations

Xiopeng XUE,Yusuke NISHIYAMA,Yoshiki NAKAMURA,Koihi MORI,Yunpeng WANG,ChihYung WEN

aSchool of Aeronautics and Astronautics,Central South University,Changsha 410083,China

bDepartment of Aerospace Engineering,Nagoya University,Nagoya 4648603,Japan

cInstitute of Mechanics,Chinese Academy of Sciences,Beijing 100190,China

dDepartment of Mechanical Engineering,The Hong Kong Polytechnic University,Hong Kong,China

1.Introduction

Shock/shock interactions, and wake/shock interactions appearing around two-body configurations often lead to crucial aerodynamic and aerothermodynamic problems for spacecraft at supersonic and hypersonic speeds.1–4Various shapes of two-body configurations associated with shock/shock and wake/shock interactions are used in a variety of applications in aeronautics,such as supersonic parachutes for re-entry capsules.In the Mars landing missions,the capsules reach supersonic speeds after entering Martian atmosphere and supersonic parachutes are deployed to slow the capsule down to subsonic speeds.5From the 20 century late 60s and early 70s,the supersonic parachute problems have been investigated widely using the experimental methods.6,7Mayhue6and Steinberg7et al.showed that the suspension line length ratio(i.e.,the ratio of the length of the suspension line to the diameter of the canopy)directly affects the drag coefficient of parachute system at supersonic speeds.Steinberg et al.7also presented the mutually interfering flow field between the forebody and canopy as a function of trailing distance by a water-table experiment.With advances in compute performance and numerical modeling techniques,numerical simulations of theflow fields around the two-body configurations emerged and the correspondingflow physics could be investigated in detail.Lingard et al.8,9carried out the early simulations on theflexible parachute system(including capsule andflexible canopy)under supersonic conditions,andfirst showed the aerodynamic interference between the capsule wake and the canopy shock.The effects of the capsule wake,Mach number and trailing distance on the performance of theflexible parachute were examined.Sengupta et al.10,11conducted the numerical and experimental investigations on subscale Mars Science Laboratory(MSL)parachute models(including capsule and canopy)and presented that theflow instability of the parachute system originates from the aerodynamic interference between the canopy shock and the capsule wake,and is dependent on the Mach numberMa,the Reynolds numberRe,the capsule shape,and proximity to a forebody.In order to fully understand the complex unsteadyflow field around such two-body configurations,a rigid capsule-canopy modeland the Detached Eddy Simulation(DES)method were employed by Barnhardt et al.12to investigate the effects of such wake/shock interaction on theflow instability.They illustrated that the time-dependent deficit in the wake interacts with the canopy shock,which causes theflow field around the capsule-canopy model to become highly unsteady.Gidzak et al.13,14further investigated the rigid capsule-canopy model using DES method and compared their data with those from wind tunnel tests.It was revealed that the time scale for the canopy motions is larger than the one for its drag variations.Xue et al.15simulated the rigid two-body configurations with a rather small trailing distance(X/d=2.38,d/D=0.2,capsule half-cone angle is 20°)and found that another aerodynamic interaction occurs,where the shock ahead of the capsule interacts with the shock wave ahead of the canopy,and the unsteadyflowfield around the two-body system exhibits the pulsation mode,which was caused by upstream propagation and lateral expansion of the complicated wake/shock and shock/shock system.Xue et al.16and Nishiyama17numerically and experimentally investigated the coupling effects of the trailing distance(X/d)and the ratio of the diameter of capsule to that of canopy(d/D)on the unsteadyflow field around the two-body configurations(capsule half-cone angle is 20°),whered/Dwas mainly chosen from 0.33 to 0.4,andX/dwas chosen from 1.25 to 10 for eachd/Dcase,and it was found that four unsteadyflow modes occur under the effect of trailing distance for all thed/Dcases;however,very little is understood on theflow physics of the fourflow modes and the mechanisms leading to the transition.Moreover,Xue et al.18further presents that the capsule half-cone angle(10°–30°)has a significant effect on the unsteady flow mode around a two-body configuration(X/d=3.75,d/D=0.2).Hatanaka et al.19investigated the mechanism of shock oscillations ahead of a rigid hemispherical canopy in a supersonicflow.

This paper aims to further explore the supersonicflow field around the two-body(capsule-canopy)configuration,similar to the parachute system,to understand and analyze theflow physics of the differentflow modes16around the parachutelike two-body models in great detail,and to examine the mechanism leading to the transition.Numerical simulations were performed for three-dimensional(3D)rigid canopy-capsule two-body models(mimicking the supersonic parachutes)with different trailing distances at afixedd/Dvalue(d/D=0.2).The effects of the trailing distance on theflow field will be thoroughly investigated.The computational results will be compared with the experimental data from the Institute of Space and Astronautical Science(ISAS)/Japan Aerospace Exploration Agency(JAXA).17

2.Two-body models

Fig.1 Two-body model used in present computation and grid of two-body model for Case C.

The rigid two-body system employed in the numerical simulations consists of a capsule and a canopy.The two-body model is shown in Fig.1(a).The original shape of canopy is a hemisphere with the diameterDof 120 mm and the thicknesshof 5 mm.The diameter of capsule frontal surface,d=24 mm,and it takes a conical form with a half-cone angle of 20°.Xis the axial distance from the capsule frontal surface to the inlet of the canopy,andX/dthe two-body trailing distance.This configuration is the same as the model used in the experiments at JAXA.The capsule and the canopy are connected with a rod(its diameter isd1)and the entire two-body model is supported at the top of the canopy by a thicker rod(its diameter isd2)to the wind tunnel model mounting system.The pointQis located inside the canopy,pointOat the capsule edge and pointTat the junction of the connecting rod and the canopy.Notably,the effects of the rod between the capsule and canopy have been investigated in the earlier study.15It was found that except for minor differences in the shock shape caused by this connecting rod,its effects on theflow field and pressure distribution on the body surfaces were rather small,and the pulsation mechanism for the case without rod was identical to that for the case with rod.

In this study,the cases with different trailing distances were conducted to investigate the effect of trailing distance(X/d)on the flow instability.The specifications for these cases are listed in Table 1.It should be noted that the diameters of the capsule and the canopy werefixed tod=24 mm andD=120 mm(d/D=0.2)in all the cases andX/d=2.5 of Case B is close to that of Ref.15in whichX/d=2.38.In addition,all the cases here were just employed for the conclusive comparison among differentd/Dcases in Ref.16,without detailed results and analysis.The present study will further understand and analyze theflow physics of the different flow modes16around the parachute-like two-body models in great detail,and to examine the mechanism leading to the transition.Note that Cases A-D have the corresponding experimental model data from JAXA,and Cases E-H are extended to examine the effect of trailing distance on the unsteady flow field around the twobody system.

3.Computational conditions and methods

3.1.Computational conditions

The freestream conditions used in the calculation are consistent with those in the experiments17.The freestream Mach numberMa∞is 2.0,the unit Reynolds numberReis 2.04×107,the total pressurep0is 160 kPa,the freestream pressurep∞is 20.3 kPa,and the dynamic pressureqis 59.2 kPa.

3.2.Numerical methods

The 3D compressible Navier-Stokes equations were solved to simulate the supersonicflow fields around the two-body models.The calculations were conducted by using an in-house parallel structured single-block code.The Simple High-resolution Upwind Scheme(SHUS)20was employed to evaluate the inviscidfluxes,and its accuracy was improved by the 3rd-order MUSCL scheme21with the Van Albadaflux limiter.22Contrarily,the viscous terms were solved by the 2nd-order central differencing scheme.The coefficient of viscosity was handled according to Sutherland’s law.In addition,time advancement was conducted by the 3rd-order total variation diminishing Runge-Kutta scheme23to obtain time-accurate results in unsteady calculations.The dimensionless time step is set to be 1.0×10-5,which is defined ast1=tV∞/D15,24(heretis the time,andV∞is the freestream velocity)in order to maintain the Courant-Friedrichs-Lewy number of about 0.5.In the calculations,all conservative variables at the inflow boundary were determined by the freestream values.The conservative variables at the outer boundary were computed from the solution inside the computational domain(zero gradient condition).The no-slip and adiabatic conditions were adopted to treat the boundary surfaces of the solid body.

No turbulence model was adopted in the present study,because the laminar numerical simulations were performed on the rigid two-body model satisfactorily with good agreement with experimental data.15,16,18The conclusions of the early studies15,16,18are reasonable despite the lack of proper turbulence modeling,which is a testament to the general observation that some aspects of theflow fields around the current two-bodyconfigurationsaredominated byinviscid gas dynamic effects(shock interactions).Therefore,the same numerical code of Xue et al.15,16,18is extended and applied in the present calculation.Nevertheless,DES method will be used to further investigate the mechanism of the complicated unsteadyflow field in the near future.

Table 1 Specifications for all cases in this study(d/D=0.2).

3.3.Grids

In the present study,a structured,single-block grid was constructed to perform the simulation of 3D rigid two-body model.The grid was created by a meridional plane because of the axisymmetric configuration of the two-body system.Fig.1(b)presents the 3D view of the grid for Case C.The grid convergence test was conducted in the previous validation study for the numerical code,where its grid density is shown sufficient to resolve the slipstream and the vortical structures.15Accordingly,a similar grid density is employed for all the cases in the present study.The grid numbers of the Cases A-H increase from about 3.3 million to 4.5 million,accordingly,with the increase of the distance between the capsule and the canopy.

3.4.Validation of numerical methods

Case C(X=90 mm)is taken as the example.The numerical simulation results are compared with the time-resolved pressure of pointQon the inner surface of the canopy(Fig.1(a))measured by high-frequency pressure transducers(Kulite XT-190-200A,nature frequency is about 380 kHz)at ISAS/JAXA.For the experimental details,please see Ref.17As shown in Fig.2,the pressure datap/p∞from the calculation is in reasonable agreement with the data measured by the experiment.17

Fig.2 Comparison of time-resolved pressure between experiment and CFD at point Q on two-body model in Fig.1(a)for Case C(X=90 mm).

Fig.3 demonstrates the representative experimental and numerical instantaneous flow fields at timeA,BandCin Fig.2.As seen,the experimental and numerical results are in reasonable agreement,apart from some differences due to the 3D effects in the experimental results.From Fig.3,it can be found that in case C(X=90 mm,X/d=3.75),the shock wave ahead of the capsule in both experiment and CFD,exhibiting a hemisphere shape,inflates and moves outward in the radial direction,which is the feature of the pulsationflow mode mentioned in the early literatures.4,15,16,18,24The mechanism of this pulsation mode for the two-body system,caused by the upstream propagation and lateral expansion of the complicated capsule wake/canopy shock and capsule shock/canopy shock interaction systems,has been investigated in detail in our earlier study.15

Fig.3 Schlieren images in experiment and their corresponding density gradient contours in numerical simulations at time A,B and C in Fig.2.

4.Results and discussion

It is found in Ref.16that theflow features vary with the distance between the capsule and canopy,X.In the current study,three differentflow regimes are further discussed:(A)pulsationflow mode,(B)oscillation mode,and(C)wake/shock interaction mode.From Refs.15–18,the representative flow structures of the threeflow regimes were observed and examined,and here the flow physics will be investigated for the three flow regimes in great detail to understand the mechanism leading to the transition between theflow regimes.

Hered/D=0.2 isfixed in the present study.When the distance between the capsule and canopy,X,is smaller than about 160 mm(X/d＜6.67),corresponding to the Cases A,B,C,D and E,the similar unsteady mode prevails.A regime of the pulsationflow mode is observed,which is resulted from capsule wake/canopy shock and capsule shock/canopy shock interactions because of the proximity of the two objects and strong interference of the shock systems.15–18As shown in Fig.4,the ratio of the stand-off distance of shock wave ahead the capsule,Δ,and the diameter of capsule frontal surface,d,for some cases are plotted to define the unsteady flow mode as a consequence of varying trailing distance(X/d).In Fig.4,t1is the non-dimensional time,and is defined ast1=tV∞/D.15,24It can be seen that there is a greater vibration in stand-off distance in Cases D and E(X＜160 mm),which clearly illustrates that the pulsation mode characterizes theflow,and the fore shock(capsule shock)periodically moves upstream and downstream with time.

As the trailing distance increases,the capsule shock/canopy shock waves become gradually decoupled but still interacting,which establishes a second regime,oscillation mode.Thefluctuation amplitude decreases.Contrarily,the fore shock formed ahead of the capsule(capsule shock)shows rather mild oscillation phenomenon(oscillation unsteady mode4,16,25)in Case F.As the trailing distance continues to increase,a third regime is formed,where only the capsule wake interacts with the canopy shock.No significant oscillation is observed in Cases G and H,which suggests no shock/shock interaction would occur at a large trailing distance(X/d>6.67).Detailedflow characteristics of three differentflow regimes will be depicted as follows.

Fig.4 Comparison of variation of ratio of the stand-off distance of the fore shock ahead of capsule,Δ,and the diameter of capsule frontal surface(d=24 mm)for Cases D,E,F,G and H with dimensionless time t1=tV∞/D.

4.1.Pulsationflow mode

From Refs.15–18,it is seen that the pulsation flow mode features with the complicated aerodynamic interactions of capsule wake/canopy shock and capsule shock/canopy shock.However,as the trailing distance is increased,thisflow mode is expected to take different forms along with the basicflow features.

Fig.5 Typical density gradient contours in two instantaneousflow fields for Cases A,B and D,showing flow features of aerodynamic interactions:fore wake/rear shock interaction(the left)and fore shock/rear shock interaction(the right).

Fig.5 illustrates the interestingflow features at two instants for some typical Cases A,B and D,including the capsule wake/canopy shock interaction(the left)and the capsule shock/canopy shock interaction(the right).The letters in Fig.5(b)annotate the differentflow characteristics,where‘‘W”refers to the shock wave,they are numbered in the order of their emergence,and ‘‘S” refers to the triple shock system.In the following,the fore wake refers to the wake formed from the capsule(capsule wake),the fore shock refers to the shock wave ahead of the capsule(capsule shock),and the rear shock refers to the shock wave ahead of the canopy(canopy shock).As also observed in Fig.5,the fore shock(W1)moves closer to the capsule body and takes a more conical shape,when the trailing distance becomes larger.In Case B(Fig.5(b))and Case C(Fig.3),two shock waves(W2 and W3)form ahead of the canopy because of the fore wake/rear shock interaction.W2 and W3 stem from the inner surface of the canopy and the center of the canopy,respectively,and are resulted from the buildup of high pressure in front of the canopy(Fig.6(a)).Notably,the mechanisms for these two shocks are different.W2 is a diffraction wave from the canopy inner surface,when the fore shock/rear shock interaction system moves downstream and interacts with the canopy inner surface in the last pulsation cycle,while W3 is its reflection wave from the connecting rod.15Thus,there is a time difference between the appearances of these two shocks.W2firstly intersects the wake,and then W3 appears in the interference region.W3 will eventually merge with W2.Theflow features of Case B(X/d=2.5)are similar to those of Ref.15(X/d=2.38).Comparatively,in Case A(Fig.5(a))whereXis rather short,W2firstly interacts with the wake,leading to a vortex region,and then it is compressed by the high pressure from the inner canopy to go directly upstream,and merges with the fore shock,W1.At this time,W3 comes to the wake region and continues to interact with the wake and then the fore shock.And,in Case D(Fig.5(c))whereXis relatively large,W2 intersects and merges with W3 in the far wake of the capsule.It is interesting to see that the time interval between the two aerodynamic interactions increases as the trailing distance extends,which is about 0.14,0.22 and 0.29 times the period for the Cases B,C and D,respectively.However,in Case A,the shock W2 goes upstream and merges with W1,which yields a relatively longer time interval(0.22T30).Tis the time period for the pulsationflow mode,and the subscripts ‘‘30”, ‘‘60” and ‘‘120” indicate the trailing distances in mm.Because of these differences mentioned above,the pressure inside the canopy becomes larger as the trailing distance is decreased.

Regarding the fore shock/rear shock interaction,it can be seen from the right side of Fig.5(a)that,in Case A,the interaction of the two shocks occurs in the lateral direction of the two-body system,and a significant vortex ring can be observed at the foot of W2,which is a consequence of a strong pressure gradient across the shock W2.When the capsule wake interacts with the shock wave W2,this vortex ring forms and entrains thefluid into the wake region in the reverse direction.It is the key mechanism for the pulsation mode.15,24In the other cases,this vortex ring also plays a similar role in the pulsation phenomenon of the two-body system,and locates at the foot(hook shape)of W2(merged with W3,as shown in the red circles in Fig.5(b)-(c)).From comparison with the nonpulsationflow mode(see the next sections),it is further found that the vortex ring and strong fore shock/rear shock interaction system work together to complete the pulsation flow field around the parachute-like two-body system.As the trailing distance(X/d)increases,the effect of shock/shock interaction on the two-body system weakens,which correspondingly weakens the pulsation flow field.In Case B(Fig.5(b)),the shock/shock interaction occurs in the middle of the capsule and the canopy and the triple shock system S around the capsule inclines toward the capsule,which causes the increase of the pressure around the capsule(Fig.6(b)),leading to the lateral expansion of the triple shock system.15Complexflow feature is exhibited.When the trailing distance keeps increasing(as in Cases C and D),the shock/shock interaction location translates close to the canopy and away from the capsule(Fig.7).The triple shock system moves downstream and consequently appears normal to the connecting rod.

To further validate the numerical results,the pulsation Strouhal numbers,St,for Cases A,B,C and D are compared with the experimental measurements in Fig.8.Here the pulsation Strouhal number,which describes the frequency offlow oscillations26,is defined as follows:

wherefis the oscillation frequency.Here the experimental and CFD oscillation frequencies were extracted from the pressure data of pointQ(Figs.1(a)and 2)via power spectrum analysis.Good agreement is observed.Stbecomes smaller as the distance between the capsule and canopy becomes larger,which indicates that the frequency(time period)for the pulsationflow reduces(increases).Note that the pulsation mode ceases at a large trailing distance(X/d>6.67)and the cutoff trailing distanceX/dis between 6.67(Case F)and 8.33(Case G).The linearSt-X/drelationship can be correlated asSt=0.219–0.004X/dfor 1.25≤X/d≤6.67.

In addition,the Strouhal numbers of experimental or numerical pressure data at pointQ(Figs.1(a)and 2)for typical Cases D,E and F are also compared with those from the stand-off distance of fore shock in Fig.8.It can be seen that the frequencies of pressure change inside the canopy are consistent with the flow field pulsating frequencies.Also shown in Fig.8 are the Strouhal number derived from numerical pressure data at pointQwith thed/D=0.4 case16to compare with that ofd/D=0.2 in this study.It can be seen that the slopes ofSt-X/dlinear relationship increase asd/Dincreases.This slope change also suggests that,whend/Dincreases,theflow mode transition from pulsation to oscillation becomes more sensitive to the change in the trailing distance and occurs at a smaller valueofX/d(d/D=0.2,X/d=6.25 andd/D=0.4,X/d=2.92).16

Fig.7 Schlieren images in experiment for Case D(X=120 mm,X/d=5.0).

Fig.8 Comparison of experimental and CFD Strouhal numbers for effect of trailing distance with d/D=0.2.The symbols▲,◆and■represent data based on the experimental pressure variation at point Q,CFD pressure variation at point Q,and CFD stand-off distance variation of the fore shock,respectively.The solid line stands for the linearfit to the Strouhal number based on the CFD pressure variation at point Q.Also shown are the data(symbol )with d/D=0.4,which is reproduced from CFD pressure variation at point Q in Ref.16,for comparison with d/D=0.2 in this study.

Fig.9 shows the comparison of experimental and CFD averaged pressure distributions on the inner surface of the canopy for Cases A,B and D in this study,whererrepresents the arc distance along the surface from the center,andLthe maximum arc length of the canopy.It can be seen from Fig.9(a)-(c)that the computational results are in good agreement with the experimental data for Cases A,B and D quantitatively.Moreover,the comparison of experimental and CFD averaged pressure distributions for Case C can be seen from Ref.18In addition,it can be found from Ref.16that:(A)in the pulsationflow mode,corresponding to the fact that the trailing distanceX/dis less than about 6.67(X≤160 mm,including Cases A,B,C,D and E)here,the averaged pressure on the inner surface of the canopy decreases with the increase of the trailing distance;(B)in the non-pulsationflow mode,corresponding toX/d>6.67 here,there is a turning point for the averaged pressure distribution atX/dof about 8.33(X=200 mm).Note that from Figs.4 and 5,Cases A,B,C,D and E show the similarflow mode(pulsation mode)and a greater vibration in stand-off distance of fore shock ahead of the capsule;however,thefluctuation amplitude of stand-off distance rapidly decreases in Case F and there is no significant oscillation of stand-off distance in Cases G and H.

4.2.Oscillationflow mode

As the trailing distance increases,the interaction between fore shock/rear shock waves becomes less significant and a secondflow characteristic regime,oscillation mode,emerges.The flow features for the oscillation mode can be seen in Ref.16,here,in order to clarify the content,and the typicalflow features of Case F are presented,including the fore wake/rear shock interaction(near central part before the canopy in Fig.10(a))and the interaction between the fore shock and the expansion fan/-contact from the rim of the capsule(right behind the fore shock in Fig.10(c)).The contact is clearly seen from the shear(Kelvin-Helmholtz)instability that develops.The weak interaction between fore shock/rear shock waves can only be seen on the bottom right of Fig.10(c).Interestingly shown is that the capsule wake is not closed,which may be affected by the connecting rod.Thisflow feature has been observed in the experimental images in the same regime as well.17A separate study by the authors,considering the two-body configurations without the rod,shows that the wake closes.27Nevertheless,the effects of the rod on the pressure distribution and pulsatingflow nature are rather insignificant.

Another interestingflow structure is clearly seen in Fig.10(b),where a series of shock waves W1,W2 and W4,compression waves,and expansion waves originate from the shear(Kelvin-Helmholtz)instability contact.Although this similar complicated wave system also occurs in the pulsation mode cases,its effect on the unsteady flow field is rather weak.In Case F,the complex fore wake/rear shock interaction causes the fore shock W1 to oscillate in both streamwise and traverse directions(Fig.10).

Notably,only the lateral part of the fore shock W1 shows rather mild oscillation phenomenon in Fig.10.Compared with that of the pulsation mode,the stand-off distance of the fore shock W1 has a weak periodical change(Fig.4).As a result,the pressure inside the canopy and around the capsule becomes rather smaller than that of pulsation mode(Figs.6 and 11).Moreover,the fore shock W1 changes periodically from contraction to expansion in a convex shape and is termed as‘‘oscillation mode”.This unsteady flow model is defined with reference to Refs.4,16,25.

Fig.9 Comparison of experimental and CFD averaged pressure distributions on inner surface of canopy.

Fig.10 Typical density gradient contours in three instantaneous flow fields for Case F,showing flow features of aerodynamic interactions.Also shown below each density gradient contour is the pressure trace as a function of x(axial distance).

Compared with the pulsation mode,it can be found that the driving mechanism of the oscillation mode produced by the two-body system is also determined by a periodic pressure imbalance between the capsule and the canopy,15and is caused by the upstream propagation and lateral expansion of the wake/shock interaction system.These phenomena are similar to that for the pulsation mode.However,the pressure imbalance exhibits a very different distribution compared with that in pulsation mode15,as shown in Fig.12.In Case F,when the pressure at the junction of the connecting rod and the canopy,pointT(Fig.1(a)),reaches to the peak level 1,there are three local maximum values due to the series of waves W and W4 shown in Fig.10(b);meanwhile,the pressure at capsule edge(pointO)almost reaches the lowest value.Contrarily,when the pressure at capsule edge reaches to the peak value,the one at pointTis almost the lowest.That is to say,when the fore wake/rear shock interaction occurs,the pressure at the junction of the connecting rod and the canopy is at its peak,which forces the interaction system to move upstream and expand laterally and generates a series of W and W4(Fig.10).At the same moment,the pressure around the capsule is at its lowest value,and the fore shock moves closest to the capsule,yielding the contraction in the fore shock pro-file.After the fore wake/rear shock interaction system moves upstream and expands laterally,the pressure inside the canopy reduces to its lowest value,and the pressure around the capsule edge reaches to its maximum value.Consequently,the fore shock is moved upstream and expands laterally,resulting in the expansion of the fore shock in a convex shape(Fig.10(c)).In addition,comparing the time histories of pressure at pointQin Case C(Fig.2,pulsation mode)and Case F(Fig.12),we can see that there is a much more complicated change in the oscillation mode,and a smaller peak level 2 of pressure happens after the peak pressure around the capsule;that is to say,the lateral expansion of the fore shock,and its weak interaction with the shock wave W4 lead to a smaller peak pressure(level 2)inside the canopy.Consequently,in the oscillation mode,the unsteadyflow field goes through different changes in sequence:(A)the wake/shock interaction occurs,(B)the wake/shock interaction system moves upstream and expands laterally,and(C)the wake/shock interaction system then forces the fore shock to move upstream and to expand laterally.This flow phenomenon is significantly different from that of the pulsation mode presented in the above section.

4.3.Wake/shock interaction

As the trailing distance continues to increase,a third regime forms,where only the capsule wake interacts with the canopy shock.From Ref.16,it can be known that in the third regime,the pressure on the inner surface of the canopy reduces to its minimum value as the trailing distance increases to a critical value,and then the pressure becomes larger again as the trailing distance continues to be increased.In this study,as the trailing distanceX/dis larger than 6.67(X>160 mm),the pressure on the inner surface of the canopy keeps decreasing untilX/d≈8.33(X≈200 mm).The pressure distribution reaches a minimum atX/d≈8.33 and increases again.The pressure distribution of Case H(X=240 mm)becomes almost the same as that of Case F(X=160 mm).

Fig.11 PressurecontoursforCaseF (X=160 mm,X/d=6.67).

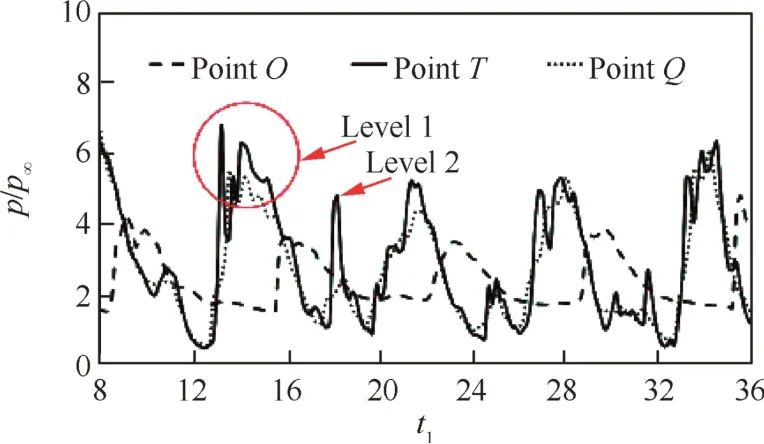
Fig.12 Comparison of time histories of pressure at points O,T and Q on two-body model in Fig.1(a)for Case F(X=160 mm).

From Ref.16,it can be found that for the third regime,the interaction of the fore shock and rear shock seems to disappear because of the larger distance between the capsule and the canopy.As a consequence of this effect,the fore shock which is formed ahead of the capsule shows no significant oscillation in Cases G and H(Fig.4),which suggests that no pulsation mode occurs in the large distance(X/d>6.67)and reveals that the unsteady fore shock/rear shock interaction in Cases A-E is a key mechanism for the pulsation mode.Moreover,the interaction of the capsule wake and the canopy shock is the main characteristic of theflow fields for Cases G and H.16This interaction provides the main source of the unsteadiness in theflow field.10,28

In addition,whenX/d＜8.33,the unsteady flow mode,such as the pulsation mode or the oscillation mode,leads to a larger pressurefluctuation inside the canopy(Fig.13).This should be strongly avoided due to its possible effect on the canopy shape change.WhenX/d>8.33,for instance in Case H,X/d=10,only the interaction of the capsule wake and the canopy shock is observed,which leads to a smaller pressurefluctuation inside the canopy.Although the canopy shape change caused by thefluid structure interaction is not considered here,this large trailing distance(X/d=10)increases the average pressure and reduces pressurefluctuation inside the canopy(Fig.13),therefore improving the unfavorableflowfield.This larger trailing distance is adopted for the supersonic parachute(capsule-canopy system).11

4.4.Total force due to pressure

Fig.13 Comparison of pressure history of point Q(Fig.1(a))for Cases E,F,G and H.

Finally,the time histories of the total axial and lateral forces due to pressure,FxandFy,on the two-body system are shown in Fig.14.The total axial and lateral forces due to pressure were calculated by(∯PdA)xand(∯PdA)y,respectively.In the axial direction,the total force acts as a drag force for the twobody configuration.From Fig.14(a),it can be seen that the smallestdragforceoccursinCaseG (X/d=8.33,d/D=0.2).The variation of the drag forces in these cases with the increasing trailing distance has a similar trend as the pressure distribution inside the canopy.

The total force acts on the two-body configuration in the lateral direction may cause the lateral motion and significantly affect the performance of two-body configuration.From Fig.14(b),it is interesting to see that the thirdflow mode causes the smallest force and the corresponding variation in the lateral direction due to the weakest wake/shock interaction.In addition,thefigures suggest that a largeX/dvalue is favorite for the stability performance of the two-body system,and even the average drag force is comprised.

Fig.14 Comparison of time history of total force due to pressure for Cases A,B,D,F,G and H.

5.Conclusions

In the present study,the supersonicflow over 3D rigid twobody models was numerically simulated at a freestream Mach number of 2.The effect of the trailing distances(X/d)between the capsule and canopy were further examined at afixedd/Dvalue(d/D=0.2)in great detail,and three differentflow regimes are summarized under the effect of trailing distance:(A)pulsationflow mode,(B)oscillation mode,and(C)wake/shock interaction mode.Here theflow physics of the threeflow regimes are deeply understood and analyzed in great detail,and the results obtained in this study are summarized as follows:

(1)The computational results in cases A,B,C and D agree with the experimental data of ISAS/JAXA.In the pulsation mode observed here(Fig.5),W2 and W3 results from the buildup of high pressure inside the canopy.When the trailing distance is short,W2 and W3 interact with the wake and fore shock W1 chronologically.When the trailing distance is increased,W2first interacts with the wake,and merges with W3,and then interacts with the rear shock.However,as the trailing distance keeps increasing,W2first merges with W3,and then interacts with the fore wake and fore shock W1.Because of this difference,the shorter the trailing distance is,the stronger the aerodynamic interactions become,and the more unstable theflow fields around the parachute-like twobody system are.

(2)The vortex ring and the strong fore shock/rear shock interaction work together to drive the pulsationflowfield around the parachute-like two-body system.

(3)The pulsation mode ceases at a large trailing distance(X/d>6.67)and the cutoff trailing distanceX/dis between 6.67(Case F)and 8.33(Case G).The linearSt-X/drelationship can be correlated asSt=0.219–0.004X/dfor 1.25≤X/d≤6.67.

(4)The driving mechanism for the oscillation mode is similar to that for the pulsation mode.However,in the oscillation mode,the unsteady flow field goes through different changes in sequence:(A)the wake/shock interaction occurs,(B)the wake/shock interaction system moves upstream and expands laterally,and(C)the wake/shock interaction system then forces the fore shock to move upstream and to expand laterally.Therefore,there is a big time interval between the two peak levels(Fig.12)of pressure inside the canopy.This is significantly different with the pulsation mode presented in this paper.

(5)In the wake/shock interaction mode,a smaller pressurefluctuation inside the canopy is observed,and no significant vibration in stand-off distance of capsule shock is present,and the unfavorableflow field is improved.

(6)The larger trailing distance leads to a smaller lateral total force and the corresponding force variation,which is favorable for the performance of the parachute-like two-body system.

In the present study,seen from Fig.6,a large stagnationflow occurs when there is no vent on the canopy.Therefore,some differences in the effects of the trailing distance may be induced by the vent holes.Further numerical simulations will be conducted to explore theflow-structure interaction in aflexible two-body model with vents based on a new elliptic grid generation method29,with the turbulent effects taken into account.

Acknowledgements

This research is substantially supported by the National Natural Science Foundation of China(No.11702332).

1.Cai C.Numerical simulations of high enthalpyflows around entry bodies.Chin J Aeronaut2016;29(2):326–34.

2.Agostini L,Larcheveque L,Dupont P.Mechanism of shock unsteadiness in separated shock/boundary-layer interactions.Phys Fluids2015;27(12):126103.

3.Kitamura K,Men’shov I,Nakamura Y.Shock/shock and shock/boundary-layer interactions in two-body configurations.35thAIAAfluid dynamics conference and exhibit.Reston:AIAA;2005.p.1–12.

4.Panaras AG,Drikakis D.High-speed unsteadyflows around spiked-blunt bodies.J Fluid Mech2009;632:69–96.

5.Cruz JR,Lingard J.Aerodynamic decelerators for planetary exploration:past,present,and future.2006 AIAA guidance,navigation and control conference and exhibit.Reston:AIAA;2006.p.1–20.

6.Mayhue RJ,Bobbitt PJ.Drag characteristics of a disk-gap-band parachute with a nominal diameter of 1.65 meters at Mach number from 2.0 to 3.0.Washington,D.C.NASA；1972.Report No.:NASA-TN-D-6894.

7.Steinberg S,Siemers PM,Slayman RG.Development of the Viking parachute configuration by wind-tunnel investigation.J Spacecraft Rock1974;11(2):101–7.

8.Lingard J,Darley M.Simulation of parachutefluid structure interaction in supersonicflow.18th AIAA aerodynamic decelerator systems technology conference and seminar.Reston:AIAA;2005.

9.Lingard J,Darley M,Underwood JC.Simulation of Mars supersonic parachute performance and dynamics.19th AIAA aerodynamic decelerator systems technology conference and seminar.Reston:AIAA;2007.p.1–11.

10.Sengupta A.Fluid structure interaction of parachutes in supersonic planetary entry.21st AIAA aerodynamic decelerator systems technology conference and seminar.Reston:AIAA;2011.p.1–12.

11.Sengupta A,Steltzner A,Comeaux K,Candler G,Barnhardt M.Results from the Mars Science Laboratory parachute decelerator system supersonic qualification program.2008 IEEE aerospace conference.Piscataway(NJ):IEEE Press;2008.p.1–15.

12.Barnhardt M,Drayna T,Nompelis I,Candler GV,Garrard W.Detached eddy simulations of the MSL parachute at supersonic conditions.19th AIAA aerodynamic decelerator systems technology conference and seminar.Reston:AIAA;2007.p.1–11.

13.Gidzak V,Barnhardt M,Drayna T,Nompelis I,Candler GV.Simulation offluid-structure interaction of the Mars Science Laboratory parachute.26thAIAAappliedaerodynamics conference.Reston:AIAA;2008.p.1–11.

14.Gidzak V,Barnhardt M,Drayna T,Nompelis I,Candler GV.Comparison offluid-structure interaction simulation of the MSL parachute with wind tunnel tests.20th AIAA aerodynamic decelerator systems technology conference and seminar.Reston:AIAA;2009.p.1–12.

15.Xue X,Koyama H,Nakamura Y.Numerical simulation on supersonic aerodynamicinteraction ofaparachutesystem.Trans Jpn Soc Aeronaut Space Sci Aerospace Technol Jpn2013;11:33–42.

16.Xue X,Koyama H,Nakamura Y,Mori K,Wen CY.Parametric study on aerodynamic interaction of supersonic parachute system.AIAA J2015;53(9):2796–801.

17.Nishiyama Y.Aerodynamic characteristics of the supersonic parachute with its opening process[dissertation].Nagoya:Nagoya University;2013.

18.Xue X,Nishiyama Y,Nakamura Y,Mori K,Wen CY.Numerical investigationoftheeffectofcapsulehalf-coneangleonasupersonic parachute system.J Aerospace Eng2016;29(4):06016001.

19.Hatanaka K,Rao SMV,Salto T,Mizukaki T.Numerical investigations on shock oscillations ahead of a hemispherical shell in supersonic flow.Shock Waves2016;26(3):299–310.

20.Shima E,Jounouchi T.Roe of CFD in aeronautical engineering(No.14)-AUSM type upwind schemes-.Proceedings of 14th NAL symposium on aircraft computational aerodynamic;1997.p.41–6.

21.Van Leer B.Toward the ultimate conservative difference scheme.IV.A new approach to numerical convection.J Comput Phys1977;23(3):276–99.

22.Anderson WK,Thomas JL,Van Leer B.Comparison offinite volumeflux vector splitting for the Euler equations.AIAA J1986;24(9):1453–60.

23.Shu CW,Osher S.Efficient implementation of essentially nonoscillatory shock-capturing schemes.J Comput Phys1988;77(2):439–71.

24.Feszty D,Badcock KJ,Richards BE.Driving mechanisms of highspeed unsteady spiked bodyflows,Part 1:pulsation mode.AIAA J2004;42(1):95–106.

25.Feszty D,Badcock KJ,Richards BE.Driving mechanisms of highspeed unsteady spiked bodyflows,Part 2:oscillation mode.AIAA J2004;42(1):107–13.

26.White FM.Fluid mechanics.4th ed.New York:McGraw Hill;1999.p.295–7.

27.Xue X,Nakamura Y,Mori K,Wen CY,Jia H.Numerical investigation on effects of angle-of-attack on two-body configurations.Aerosp Sci Technol2017;69(1):370–86.

28.Karagiozis K,Kamakoti R,Cirak F,Pantano C.A computational study of supersonic disk-gap-band parachutes using large-eddy simulation coupled to a structural membrane.J Fluids Struct2011;27(2):175–92.

29.Kaul U.Three-dimensional elliptic grid generation with fully automaticboundaryconstraints.JComputPhys2010;229(17):5966–79.