页岩气水平井缝内砂塞分段工艺的增产机理

李德旗 何 封 欧维宇 朱炬辉 李 然 潘 勇

1.中国石油浙江油田公司 2.中国石油川庆钻探工程公司

0 引言

目前国内外页岩气增产改造普遍采用水平井、大规模分段体积压裂，工艺以桥塞分段结合多簇射孔为主[1-2]。川渝地区页岩气储层因其应力结构复杂、埋深差异大（储层垂深普遍大于2 300 m，部分大于3 000 m）、天然裂缝及断层发育、施工压力高、改造难度相对较大等特殊性，致使以桥塞为主的机械分段工艺在川渝页岩气的现场应用中受到不同程度的制约。

根据川渝地区页岩气压裂实际情况，压裂过程中经常出现套管变形等井下复杂情况，套变点超过50%靠近A点附近，常规机械分段工具无法通过，造成大量水平井段无法得到有效改造。据统计，长宁、威远区块因套管变形受影响的压裂段长约13 700 m，受影响的压裂段数达到176段。因此，亟须一种无机械封隔、对井眼轨迹和井筒尺寸要求小、可实现无限级分段且整个施工过程保持井筒全通径的新型分段压裂工艺，为我国页岩气储层增产改造提供一种新的技术手段。

页岩水平井缝内砂塞分段压裂工艺[3]利用高砂浓支撑剂在缝口及近井形成人工砂塞，依靠砂塞的阻流作用实现不同层段的封隔及分段改造。该工艺无须机械桥塞坐封，有效规避桥塞相关作业风险、节约施工成本，最大程度减弱了套管变形对储层改造带来的不利影响。笔者针对该工艺在页岩增产改造中其缝内砂塞的导流能力及工艺参数的控制优化进一步展开理论与实验研究，并结合现场实践结果验证其适应性及有效性。

1 缝内砂塞分段高导流能力

页岩水平井缝内砂塞分段压裂工艺与常规电缆分簇射孔桥塞联作工艺相比，其最大的优点是无须电缆泵送桥塞，整个压裂施工过程中井筒保持全通径状态。该工艺主要利用压裂施工最后阶段的高砂浓度支撑剂在缝口及近井形成人工砂塞，以达到常规机械桥塞封隔分段的目的。缝内砂塞分段的效果好坏关键在于砂塞能否满足在储层闭合应力条件下的抗压强度、排液阶段能否保持稳定及高导流能力。针对以上问题，选取两种支撑剂受力模型分别研究了在储层闭合应力条件下支撑剂砂塞的抗压强度、返排投产过程中缝内砂塞力学稳定性及基于接触模型的渗透率。

1.1 闭合应力下缝内砂塞强度分析

支撑剂颗粒在滑溜水的携带作用下注入地层，随着液体流速的降低支撑剂颗粒逐渐在缝内沉积并形成无规则堆积[3]。在没有任何附加力的条件下，支撑剂颗粒将形成任意堆积，堆积结构较松散，接触不充分，堆积密度较小[4]。但在实际水力裂缝中，随着压裂流体的滤失，裂缝缝宽将逐渐变窄，支撑剂颗粒受到闭合应力的挤压及流体的携带等综合作用将由最初的任意堆积逐步形成密集堆积。根据叶大年[5]的实验研究，等大球体在密闭空间中可以形成多种不同接触关系的密集堆积。为了较全面地分析砂塞的可靠性，分别建立了堆积密度较小的体心立方模型及堆积密度最大的面心立方模型（图1）。

图1 等大球体体心立方和面心立方示意图

通常情况下，支撑剂颗粒因其生产过程诸多因素的不可控，必然导致其在尺寸大小、圆球度等方面存在一定差异。在建立支撑剂颗粒的力学模型时将其视为均质等径、完全弹性的理想球体，因此可将支撑剂颗粒接触问题转化为弹性球体间点载荷接触问题。1881年，Hertz首先用数学弹性力学方法导出表面光滑的弹性球体点载荷接触问题的计算公式[6]。针对支撑剂密集堆积模型，支撑剂之间满足点接触，受力后其接触表面为圆，符合变形连续条件；整个接触过程处于弹性阶段且服从胡克定律，因此接触表面上应力应变满足线性关系；表面接触压力所组成的合力等于外加载荷。支撑剂颗粒点接触如图2所示。

根据Hertz弹性球体点载荷接触力学假设可以导出弹性球体接触表面圆的半径Ra，两球在压应力条件下的接触形变δ及最大接触压应力qmax和压应力在接触圆内的分布[7]。式（1）是两球弹性接触非线性精细积分式[8]，忽略接触区域的水平位移则可解得球体接触表面圆的最大半径（Ra）、δ、两球在压应力条件下位于接触圆上半径r处的最大接触应力（qmax）。

图2 支撑剂颗粒点接触关系图

即

其中

式中q表示两球在压应力条件下位于接触圆上半径r处的应力，Pa；r表示为接触圆内任意半径，m；δ表示两球在压应力条件下的接触形变，m；R1、R2分别表示接触两球体的半径，m；E1、E2分别表示接触两球的杨氏模量，Pa；ν1、ν2分别表示接触两球体的泊松比，无因次；Ф表示两球体接触形变圆上半径r处的积分角，(°)。

支撑剂颗粒受到的外加载荷主要来自于储层闭合应力、流体压力及颗粒自身重力，因支撑剂的视密度仅有2.6～2.8 g/cm3，且颗粒非常细小，因此计算外加载荷时其自重可忽略不计。水力裂缝的闭合应力始终垂直于裂缝壁面（图3）。设裂缝倾角为θ，则有闭合应力为σ。考虑支撑剂颗粒在裂缝壁面的嵌入作用[9-12]，则有半径为R的支撑剂球体受到壁面闭合应力与流体压力pc的最大净载荷为p：

图3 不同裂缝倾角下闭合应力关系图

式中σ、σh、σv分别表示裂缝闭合应力、水平及垂向应力，Pa；θ表示裂缝倾角，(°)；p表示支撑剂颗粒受到的净载荷，N；pc表示流体压力，Pa；R表示支撑剂颗粒半径，m。

支撑剂球体之间的接触满足弹性球体接触，因此其破坏判断准则遵从最大剪应力强度理论，该准则表达式如下：

根据陈国辉[13]的研究表明，弹性球体接触时其最大剪应力为τmax，则有：

因此，可以应用上述力学模型判断支撑剂颗粒在屈服强度[σ′]下能否承受储层外加载荷，能否在该载荷条件下不发生强度破坏。

1.2 流体作用下缝内砂塞稳定性

支撑剂颗粒在水力裂缝中形成前文所述的接触模型，该类接触模型除了承受裂缝闭合应力之外，同时也承受施工过程中压裂流体及返排流体的冲刷作用。缝内砂塞抵抗流体冲刷作用的主要作用力来自于粗糙表面的摩擦阻力。根据库仑摩擦理论[14]，支撑剂颗粒之间的摩擦阻力与其受到的法向应力正相关，各个模型受到的摩擦阻力如图4所示。

针对体心立方，因为各个接触点相互对称，则有α=45°，所以在图4所示坐标系条件下最大静摩擦阻力F1为：

式中F1表示体心立方模型受到的最大静摩擦阻力，N；μf表示支撑剂颗粒静摩擦系数，无因次；α表示支撑剂颗粒净载荷与摩擦面夹角，(°)。

针对面心立方，除了包含体心立方中的8个接触球外还包含与流体平行的4个接触球，在图4所示坐标系条件下有F2为：

式中F2表示面心立方模型受到的最大静摩擦阻力，N。

当支撑剂颗粒之间存在流体流动时，流体黏度、气液比、流速等参数均会影响流体对支撑剂颗粒的冲刷作用。根据流体力学理论，缝内砂塞在流体冲刷作用下主要受到黏滞阻力、压差阻力等力的影响，单个支撑剂颗粒受到的总冲刷力为FD，则有：

式中FD表示单个支撑剂颗粒受到的总冲刷力，N；CD表示阻力系数，无因次；ρ表示流体密度，kg/m3；v表示流体在支撑剂球体间的流速，m/s。

因此，可以根据冲刷作用力FD与最大静摩擦阻力的相对大小来判断缝内支撑剂砂塞能否在注入及返排投产过程中保持稳定。

1.3 基于接触模型和分形理论砂塞渗透率计算方法

根据体心立方及面心立方中支撑剂颗粒的接触关系，导出它们在未受闭合应力及流体压力条件下的最大孔隙度。

在图5中，为了便于直观表达各个球体之间的接触关系，特意将各个球体进行缩小表示，并应用小圆柱体代表球体之间的相切关系。对于体心立方及面心立方模型分别有立方边长表达式m1、m2为：

对于体心立方及面心立方模型分别有孔隙度表达式 φ11、φ22为 ：

图5 等大球体体心立方和面心立方接触示意图

式中R表示为等大球体半径，m；m1、m2分别表示体心立方及面心立方模型边长，m；φ11、φ22分别表示体心立方及面心立方模型初始孔隙度，无因次。

储层条件下缝内砂塞必然受到裂缝壁面的闭合应力以及缝内流体压力的双重影响，因此实际砂塞的孔隙度要比根据几何关系导出的孔隙度低。在裂缝外加载荷作用下，支撑剂颗粒之间相互挤压，在接触面上发生形变，最终导致孔隙度进一步缩小（图6）。

图6 支撑剂颗粒接触形变示意图

应用砂塞强度理论可导出两种接触模型因外加载荷作用而分别减少的孔隙度Δφ11、Δφ22。球缺高度为δ/2，球缺截面半径为Ra，体心立方模型有8个相切接触，面心立方有36个相切接触，则有：

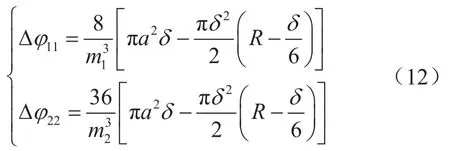
式中Δφ11、Δφ22分别表示体心立方及面心立方模型分别减少的孔隙度，无因次；a表示球缺截面半径（即球体接触表面圆的最大半径），m。

作用于缝内的流体压力通过流压变化对支撑剂颗粒孔隙产生影响。流压增加砂塞孔隙增加，流压降低砂塞孔隙减小。采用孔隙体积压缩系数Cp描述流体压力对砂塞孔隙的影响程度，Cp通过室内实验测定。尼科拉耶夫斯基 BH等[15]通过研究岩石的压缩系数Cp，提出了将常压下室内所测孔隙度转换为地层条件下的孔隙度的表达式，则有两种接触模型在储层条件下的真实孔隙度为φ1、φ2。即

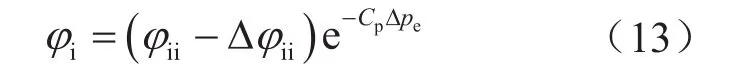
式中Cp表示孔隙体积压缩系数，MPa－1；Δpe表示流体压力变化量，MPa；φi、φii、Δφii分别表示体心立方及面心立方模型实际孔隙度、初始孔隙度、因接触变形减少的孔隙度，无因次。

缝内砂塞具有较好的几何结构，其孔渗数学关系可用分形理论描述。1975年Mandelbro BB创立的分形理论在很大程度上揭示了油气藏的宏微观性质，在多个尺度上表现了它们的分形特征及相互关系。分形多孔介质的渗透率和孔隙度都是多孔介质分维数、分形系数和微观孔隙结构参数的函数[16-17]，即

其中

式中C、D分别表示中间变量；K表示砂塞渗透率，D；φ表示孔隙度。

D为分形系数，S为分维数，二者表征了砂塞微观孔隙/孔喉结构特征，由实验数据拟合解得。由孔渗关系式可以解得缝内砂塞在储层条件下的渗透率，结合压裂裂缝参数最终可以计算出近井地带的裂缝导流能力。

2 缝内砂塞工程模拟实验

根据大量页岩储层压裂效果发现，近井缝口处的导流能力对初产及稳产有着重要影响[18-20]。因此，缝内砂塞除了要保证不同层段的有效封隔外，还需在近井地带维持较高的导流能力。目前，一般是通过提高压裂阶段最后一个携砂液砂浓度及段塞长度实现近井的高砂浓度封口，以期获取较高的近井导流能力。梁兴等[3]已在现场应用缝内填砂暂堵压裂技术，该技术缝内填砂阶段的砂浓度已远高于目前常规工艺连续加砂的砂浓度，并取得良好的增产效果。

2.1 砂塞孔隙体积压缩系数实验

参照标准SY/T 5815—2016关于孔隙体积压缩系数的测试规程，应用API标准导流室模拟缝内砂塞，设置孔隙压力5 MPa，随后测试不同上覆压力下的孔隙体积及其变化，最后应用孔隙体积压缩系数定义计算出不同净有效压力下的孔隙体积压缩系数，净有效压力为上覆压力与孔隙压力之差值。

实验结果表明（图7），孔隙体积压缩系数随净有效压力增加呈近似指数下降。在整个净有效压力测试期间，砂塞孔隙体积压缩系数在10－2～10－3MPa－1范围内波动，当净有效压力超过30 MPa时孔隙体积压缩系数随净有效压力的变化趋于平缓，其值近似为 8×10－3MPa－1。

图7 砂塞孔隙体积压缩系数实验结果图

2.2 砂塞渗透率实验

室内应用类似岩心夹持器工具制作人工模拟砂塞圆柱体，并在该工具中进行不同围压下砂塞渗透率测试，实验后砂塞圆柱体如图8所示。砂塞圆柱尺寸为r×h (10 mm×35 mm)，分别测试20目、40目、70目、100目陶粒。实验设置5 MPa回压，不同净有效压力下砂塞渗透率测试结果如图9所示。

图8 室内模拟砂塞图

图9 砂塞渗透率测试结果图

渗透率实验表明，砂塞渗透率随净有效压力增加而下降，与孔隙体积压缩系数类似。在整个净有效压力测试期间，砂塞渗透率在102～10－2D范围内波动，当净有效压力超过20 MPa时砂塞渗透率随净有效压力的变化趋于平缓。在相同净有效压力条件下，支撑剂目数越大，渗透率越高。

2.3 砂塞渗透率模型D—S参数求解

由缝内砂塞工程模拟实验所得的孔隙体积压缩系数及渗透率值可以解出基于接触力学模型和分形理论的分形系数D、分维数S。拟合结果如图10所示，分别解出不同目数支撑剂其分形系数D及分维数S。

3 缝内砂塞分段增产控制及优化

根据缝内砂塞强度理论、砂塞在流体作用下的稳定性及基于分形模型的渗透率函数关系，分析缝内砂塞在不同净有效压力、不同颗粒粒径、不同杨氏模量条件下各个参数的变化规律，以进一步评价砂塞分段工艺的适应性。

3.1 支撑剂强度控制及优选

支撑剂颗粒满足剪切破坏强度理论，如图11所示：抗剪能力随杨氏模量增加而增大；随着外载荷增加，保持颗粒完整性所需的抗剪强度亦增加；在载荷增加初期，支撑剂颗粒需具有较高的抗剪强度。

图10 砂塞渗透率模型D—S拟合结果图

图11 支撑剂颗粒剪切破坏强度图

颗粒之间的接触区域半径及形变均随杨氏模量的增加、颗粒粒径的减小、净有效应力的减小而降低；接触区域半径及形变量均是在杨氏模量最小、颗粒粒径最大、净有效应力最大处取得最大值。在如图12、13所示的参数范围条件下，接触区域半径及形变量对净有效应力、颗粒粒径、杨氏模量的敏感程度依次减弱。

3.2 砂塞抗流体冲蚀控制及优化

支撑剂颗粒在缝内形成的砂塞受到沿流体运动方向的冲蚀作用力，而颗粒之间粗糙接触表面的摩擦力是抵抗流体冲蚀力的主要贡献者，二者之间的数量关系决定着缝内砂塞抗流体冲蚀作用的稳定性。

图12 支撑剂颗粒接触区域形变半径图

图13 支撑剂颗粒接触区域形变量图

从图14可以看出，支撑剂颗粒抗流体冲蚀能力随颗粒粒径的减小而降低，当支撑剂颗粒的粒径小到一定值后，颗粒粒径对支撑剂抗流体冲蚀能力的影响将逐渐减弱。接触模型表征着颗粒之间的不同接触关系，面心立方比体心立方接触更为紧密，其受到的摩擦力更大。因此，面心立方相对体心立方稳定性更好。

以40目陶粒为例，计算在不同净有效压力条件下不同接触模型抵抗流体冲蚀作用的流体参数。在图15中，黄色、蓝色面积分别表征面心、体心立方流体冲蚀参数（CDρR2V2）的取值范围，面心立方的流体冲蚀参数近似体心立方的2倍。

3.3 砂塞渗透率分析

缝内砂塞渗透率大小对近井导流能力有着极为重要的影响。不同的接触模型、不同支撑剂强度及粒径等都将影响砂塞渗透率大小。以40目陶粒为例，其计算结果如图16～18所示。

面心立方因其接触较体心立方更为紧密，其在孔隙度及孔喉结构上要比体心立方致密。因此，面心立方砂塞的渗透率要比体心立方略小。支撑剂颗粒的杨氏模量与砂塞孔隙体积压缩系数密切相关，杨氏模量通过影响孔隙体积压缩系数而影响孔隙度及孔喉结构。图18表明，高杨氏模量的支撑剂砂塞即使在高净有效压力条件下仍具有较高的渗透率，而对于低杨氏模量支撑剂砂塞，即使净有效压力不足10 MPa，其渗透率也小于1 D。颗粒粒径主要通过影响孔喉结构而影响砂塞渗透率，支撑剂目数不同，分形系数及分维数皆不同。颗粒粒径越大，砂塞渗透率越高。

图14 最大抗冲蚀力与颗粒粒径关系图

图15 流体冲蚀参数与颗粒接触模型关系图

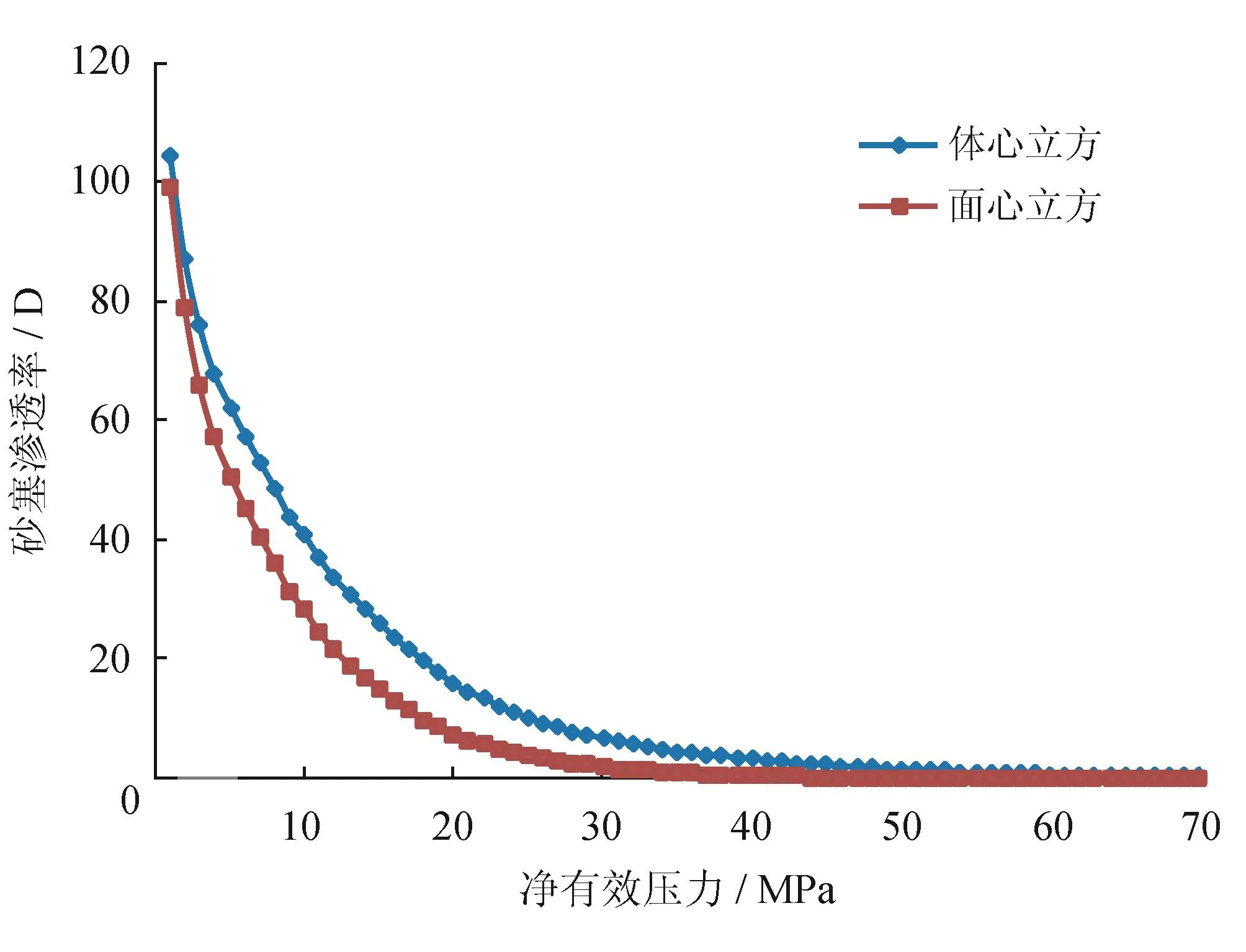
图16 接触模型与砂塞渗透率关系图

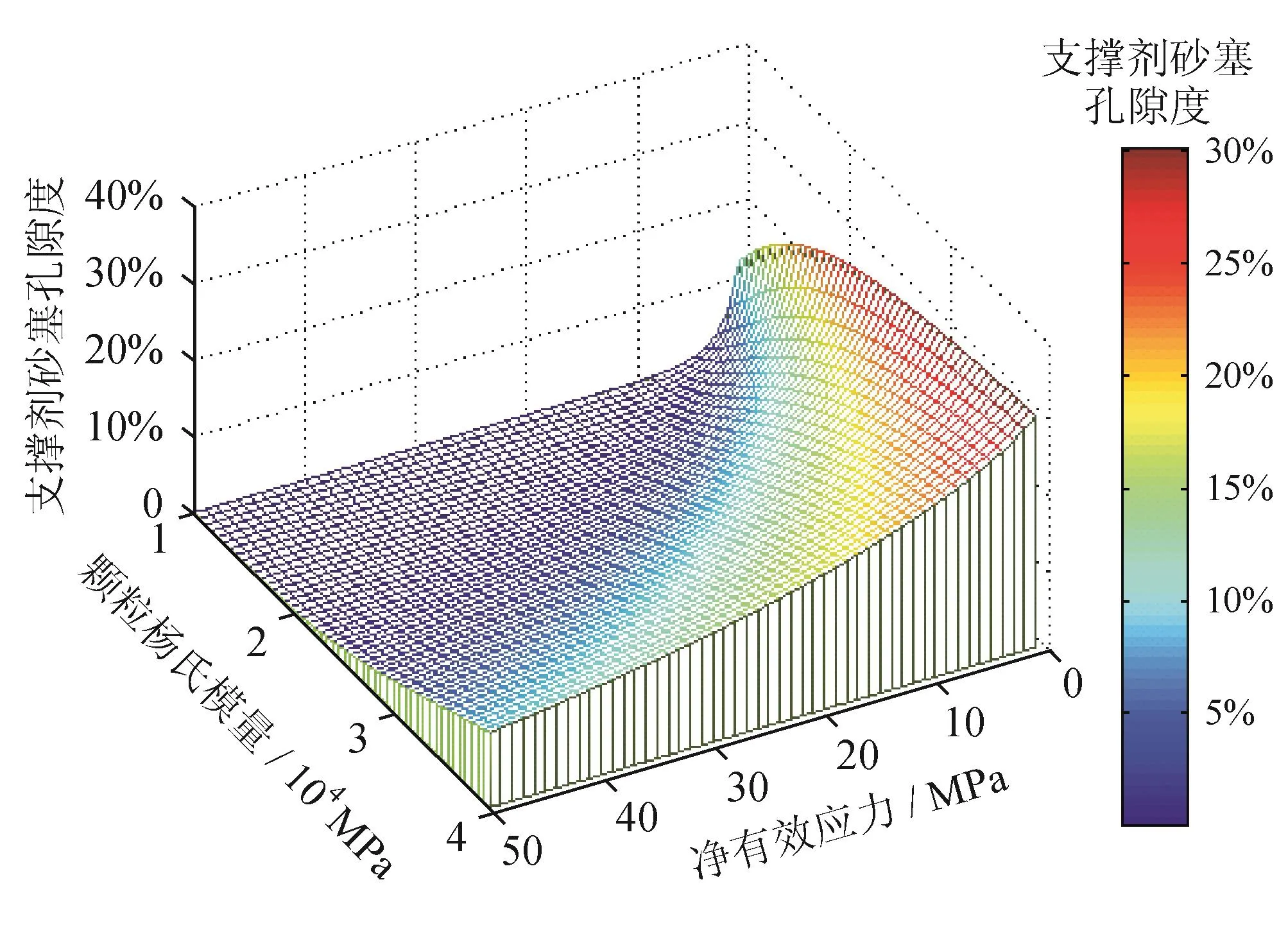
图17 砂塞孔隙度分布图

图18 砂塞渗透率分布图

4 现场实践与效果分析

ZC水平井位于四川盆地川南低陡褶带南缘，南与滇黔北坳陷相邻。该井以古生界下志留统龙马溪组黑色页岩为目的层，成像测井表明在水平段发育着不同倾角的高导缝。ZC井采用连续油管喷砂射孔＋缝内砂塞分段工艺进行增产改造，尾追阶段采用240、300、400、480 kg/m3阶梯砂浓进行缝内砂塞分段。砂塞均以40目陶粒为主，该陶粒的抗剪强度为50 MPa，杨氏模量为30 GPa，泊松比为0.25，视密度为2 600 kg/m3，静摩擦系数为0.3，在12 m3/min排量下支撑剂砂塞的流体阻力系数为3。ZC井返排初期井口套压为30 MPa，返排结束转入投产时井口套压为8 MPa。

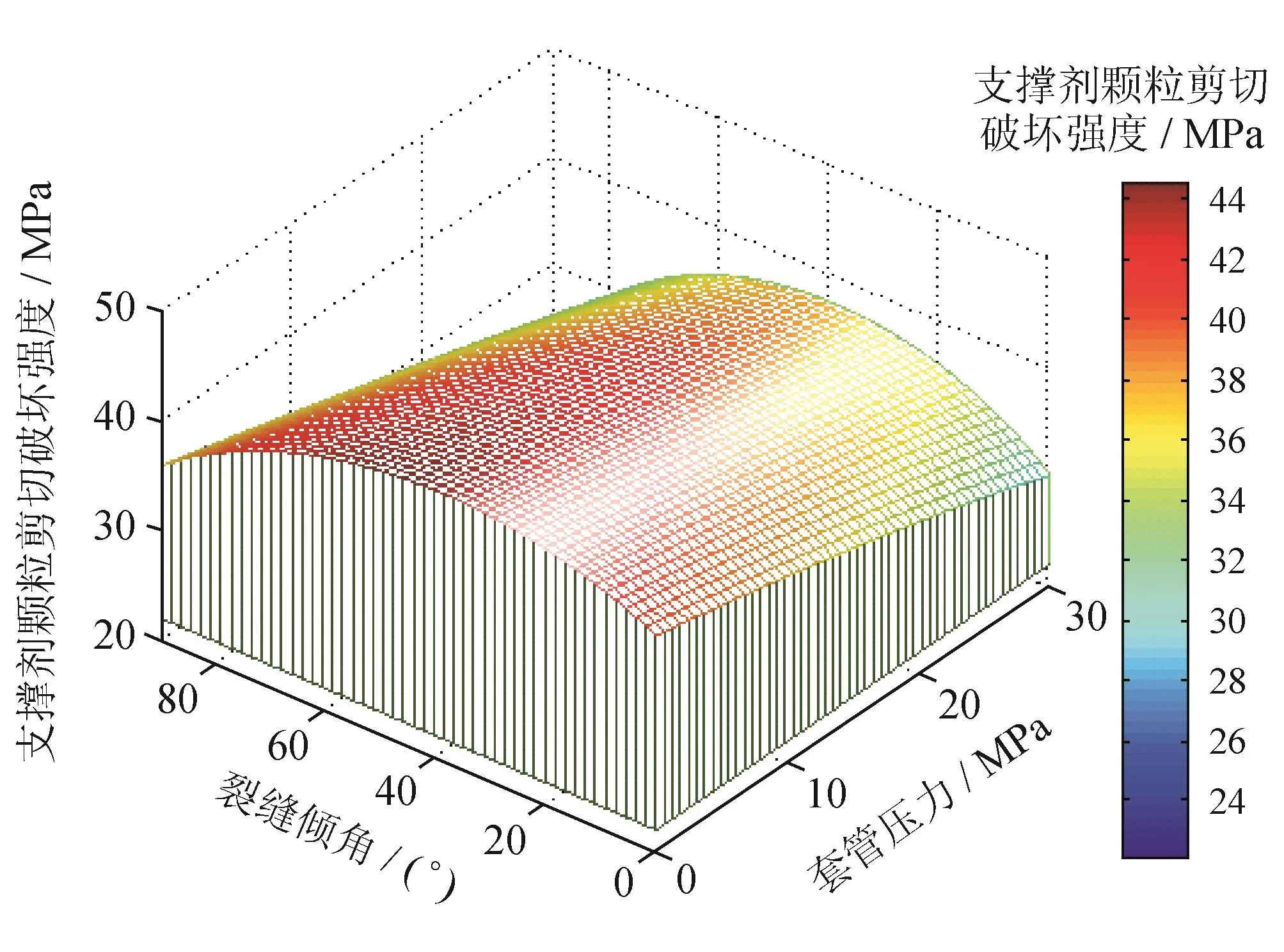
图19 砂塞抗剪强度图

根据砂塞分段理论，ZC井砂塞接触形变、渗透率及稳定性计算结果如图19～21所示。由于ZC井水平段发育不同倾角的高导缝，因此在分析砂塞参数时必须考虑裂缝倾角的影响。支撑剂所需最大抗剪强度在倾角接近40°时取得最大值，砂塞渗透率在裂缝垂直、高杨氏模量处最大，而在倾角为40°时渗透率最小，其值在1 D左右。在本例中，当井口套压为0时，裂缝倾角为40°左右处的支撑剂受到的剪切强度接近于其屈服强度，易发生支撑剂破碎损坏。

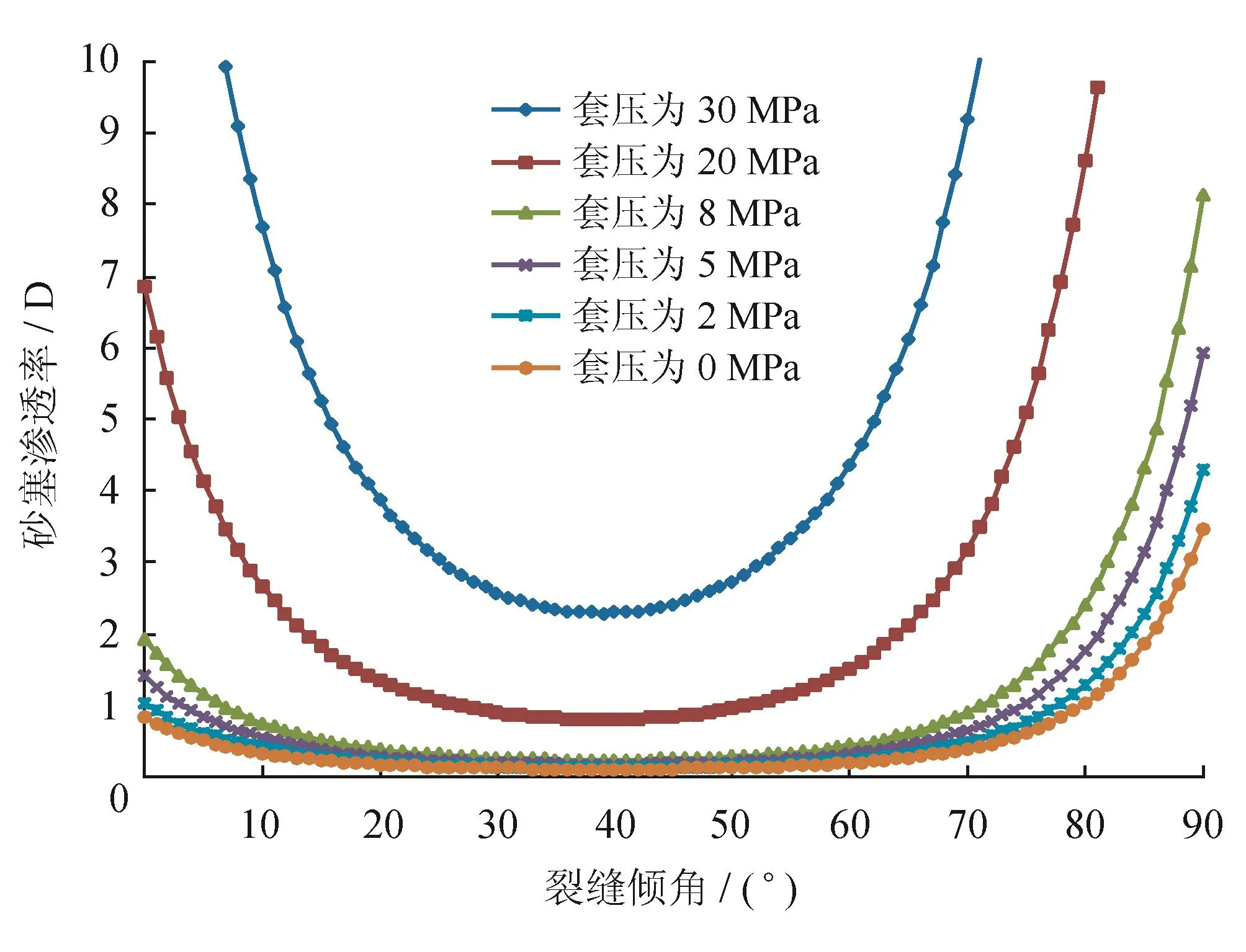
图20 ZC井井口压力与砂塞渗透率关系图

图21 砂塞抗冲蚀能力图

针对砂塞的抗冲蚀能力，选取返排初期进行模拟计算。在返排初期颗粒受到的流体压力接近55 MPa，此时净有效压力较低，抵抗冲蚀作用的摩擦阻力较小。如图21所示，体心立方（F1）模型的抗冲蚀能力比面心立方（F2）的抗冲蚀能力弱，当裂缝倾角分别高于78°、85°时，体心立方、面心立方模型中分别将发生部分支撑剂被流体冲塌现象。

ZC井应用缝内砂塞分段压裂工艺，现场分段效果如图22、23所示，各段起裂信号均出现在压裂设计层段位置，无起裂信号串层现象。微地震监测结果表明各层段均实现了有效封隔，改造规模达到了设计的改造体积，压后返排取得测试产量12×104m3/d（13 mm油嘴，井口套压8 MPa）。

图22 ZC井第4、5、6、8段起裂信号图

图23 ZC井微地震监测分段效果图

5 结论与建议

通过前文建立的支撑剂颗粒接触模型及在闭合应力与流体冲蚀作用下的稳定性、砂塞渗透率等基础研究，对ZC井的砂塞封堵参数进行了优化，经过20段现场压裂实践，进一步验证了该系列模型的适应性，得到如下认识。

1）应用球体密集堆积理论结合Hertz弹性球体点载荷接触力学所建立的支撑剂颗粒接触模型，能够良好地表征缝内砂塞的接触、受力等关系，应用分形理论表征砂塞渗透率值与实验实测模拟砂塞渗透率值，能够建立良好的数学关系，该砂塞渗透率模型对现场应用具有一定的指导意义。

2）在返排初期砂塞的稳定性主要受到流体的冲蚀作用影响，应严格控制排液速率，在生产后期砂塞的稳定性主要受到裂缝闭合应力和流压的影响，适当提高支撑剂颗粒的屈服强度对稳产具有重要意义。

3）支撑剂颗粒的杨氏模量通过影响孔隙度和孔喉结构而影响渗透率，支撑剂粒径主要通过影响孔喉结构而影响渗透率，提高支撑剂的杨氏模量是保持裂缝较高渗透率及导流能力的最有效方法。

4）针对支撑剂颗粒抗流体的冲蚀能力，支撑剂颗粒静摩擦系数、流体阻力系数及实际流速等参数需进一步开展相关实验，以完善相应研究。

[1] Jaripatke OA, Chong KK, Grieser WV & Passman A. A completions roadmap to shale-play development: A review of successful approaches toward shale-play stimulation in the last two decades[C]//International Oil and Gas Conference and Exhibition in China, 8-10 June 2010, Beijing, China. DOI: http://dx.doi.org/10.2118/130369-MS.

[2] Cipolla CL, Warpinski NR, Mayerhofer MJ, Lolon E & Vincent MC. The relationship between fracture complexity, reservoir properties, and fracture treatment design[C]//SPE Annual Technical Conference and Exhibition, 21-24 September 2008, Denver,Colorado, USA. DOI: http://dx.doi.org/10.2118/115769-MS.

[3] 梁兴, 朱炬辉, 石孝志, 张俊成, 刘臣, 何封, 等. 缝内填砂暂堵分段体积压裂技术在页岩气水平井中的应用[J]. 天然气工业, 2017, 37(1): 82-89.Liang Xing, Zhu Juhui, Shi Xiaozhi, Zhang Juncheng, Liu Chen,He Feng, et al. Staged fracturing of horizontal shale gas wells with temporary plugging by sand ベlling[J]. Natural Gas Industry,2017, 37(1): 82-89.

[4] Dai Hongqin, Bai Lun, Zhan Kuihua, Sun Ziling & Guan Guoping. Computer simulation of random packing of spherical particles in two dimensions[J]. Journal of Donghua University (English Edition), 2011, 28(1): 31-34.

[5] 叶大年. 球体任意堆积的统计几何分析[J]. 地质科学,1990(4): 324-331.Ye Danian. Statistical geometrical analysis of haphazard packing of spheres[J]. Scientia Geologica Sinica, 1990(4): 324-331.

[6] 徐芝纶. 弹性力学[M]. 4版. 北京: 高等教育出版社, 2006.Xu Zhiguan. Elastic mechanics[M]. 4thed. Beijing: High Education Press, 2006.

[7] Johnson KL. 接触力学[M]. 徐秉业, 译. 北京: 高等教育出版社, 1992.Johnson KL. Contact mechanics[M]. Xu Bingye, trans. Beijing:High Education Press, 1992.

[8] 云天铨. Hertz接触问题的精确的积分方程[J]. 应用数学和力学, 1991, 12(2): 165-169.Yun Tianquan. The exact integral equation of Hertz's contact problem[J]. Applied Mathematics and Mechanics, 1991, 12(2):165-169.

[9] Pimenov AA & Kanevskaya RD. Mathematical modeling of proppant embedment and its effect on conductivity of hydraulic fracture[C]//SPE Russian Petroleum Technology Conference,16-18 October 2017, Moscow, Russia. DOI: http://dx.doi.org/10.2118/187934-MS.

[10] Zhang Junjing, Ouyang Lianchen, Hill AD & Zhu Ding. Experimental and numerical studies of reduced fracture conductivity due to proppant embedment in shale reservoirs[C]//SPE Annual Technical Conference and Exhibition, 27-29 October 2014, Amsterdam, The Netherlands. DOI: http://dx.doi.org/10.2118/170775-MS.

[11] 吴国涛, 胥云, 杨振周, 杨立峰, 张静. 考虑支撑剂及其嵌入程度对支撑裂缝导流能力影响的数值模拟[J]. 天然气工业,2013, 33(5): 65-68.Wu Guotao, Xu Yun, Yang Zhenzhou, Yang Lifeng & Zhang Jing.Numerical simulation considering the impact of proppant and its embedment degree on fracture ぼow conductivity[J]. Natural Gas Industry, 2013, 33(5): 65-68.

[12]侯磊, Elsworth D, 孙宝江, 王金堂. 页岩支撑裂缝中渗透率变化规律实验研究[J]. 西南石油大学学报(自然科学版), 2015,37(3): 31-37.Hou Lei, Elsworth D, Sun Baojiang & Wang Jintang. Experimental study on permeability evolution in propped shale fracture[J].Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(3): 31-37.

[13] 陈国辉. 球体在接触中发生破坏的预见和计算[J]. 贵州工学院学报, 1984(增刊1): 141-148.Chen Guohui. The prediction and calculation of the failure of a sphere in contact[J]. Journal of Guizhou University of Technology, 1984(S1): 141-148.

[14] 瓦伦丁 L 波波夫. 接触力学与摩擦学的原理及其应用[M]. 李强, 雒建斌, 译. 北京: 清华大学出版社, 2011.Popov VL. Contact mechanics and friction physical principles and applications[M]. Li Qiang & Luo Jianbin, trans. Beijing: Tsinghua University Press, 2011.

[15] 杨胜来, 魏俊之. 油层物理学[M]. 北京: 石油工业出版社,2004.Yang Shenglai & Wei Junzhi. Petrophysics[M]. Beijing: Petroleum Industry Press, 2004.

[16] 李留仁, 赵艳艳, 李忠兴, 焦李成, 薛中天. 多孔介质微观孔隙结构分形特征及分形系数的意义[J]. 石油大学学报(自然科学版), 2004, 28(3): 105-107.Li Liuren, Zhao Yanyan, Li Zhongxing, Jiao Licheng & Xue Zhongtian. Fractal characteristics of micropore structure of po-rous media and the meaning of fractal coefベcient[J]. Journal of the University of Petroleum, China (Edition of Natural Science),2004, 28(3): 105-107.

[17] 李留仁, 袁士义, 胡永乐. 分形多孔介质渗透率与孔隙度理论关系模型[J]. 西安石油大学学报(自然科学版), 2010, 25(3):49-51.Li Liuren, Yuan Shiyi & Hu Yongle. A new model for describing the relationship between the permeability and the porosity of fractal porous media[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2010, 25(3): 49-51.

[18] 杜殿发, 赵艳武, 张婧, 刘长利, 唐建信. 页岩气渗流机理研究进展及发展趋势[J]. 西南石油大学学报(自然科学版),2017, 39(4): 136-144.Du Dianfa, Zhao Yanwu, Zhang Jing, Liu Changli & Tang Jianxin. Progress and trends in shale gas seepage mechanism research[J]. Journal of Southwest Petroleum University (Science &Technology Edition), 2017, 39(4): 136-144.

[19] 鄢雪梅, 王欣, 张合文, 王永辉, 段瑶瑶. 页岩气藏压裂数值模拟敏感参数分析[J]. 西南石油大学学报(自然科学版),2015, 37(6): 127-132.Yan Xuemei, Wang Xin, Zhang Hewen, Wang Yonghui & Duan-Yaoyao. Analysis of sensitive parameter in numerical simulation of shale gas reservoir with hydraulic fractures[J]. Journal of Southwest Petroleum University (Science & Technology Edition),2015, 37(6): 127-132.

[20] 贾成业, 贾爱林, 何东博, 位云生, 齐亚东, 王军磊. 页岩气水平井产量影响因素分析[J]. 天然气工业, 2017, 37(4): 80-88.Jia Chengye, Jia Ailin, He Dongbo, Wei Yunsheng, Qi Yadong &Wang Junlei. Key factors influencing shale gas horizontal well production[J]. Natural Gas Industry, 2017, 37(4): 80-88.