量子纠缠的超空间转移理论方案的探讨

2018-02-01肖骏

科技与创新 2018年3期

肖骏

（长春理工大学理学院，吉林长春 130022）

1 概述

量子纠缠，或称量子缠结，是一种量子力学现象，也是量子力学最重要的特征之一。“纠缠”这一名词的提出可以追溯到量子力学诞生之初。量子纠缠是1935年由爱因斯坦、波多尔斯基和罗森提出的一种波，最早是用来证实他们认为“物理量的实际值先于测量值”的观点[1]。最早的连续变量纠缠态是由他们提出的EPR态，对量子力学的基本原理和概念诠释提出了质疑。也就是说，自然界不存在超光速的相互作用。1964年，爱尔兰物理学家Bell提出了著名的Bell不等式，将验证量子纠缠从哲学引入到了可由实验验证的层面。1982年，法国Aspect小组在Ca40原子在级联跃迁过程中辐射出的纠缠光子的实验中，首次验证了量子纠缠。而后，1998年，奥地利Innsbruck大学的Zeilinger小组进一步完善了这一实验认证[2]。

在20世纪末期，随着算法的不断改进，比如大数分解质因子这类的经典加密方式也不再安全了，人们对信息保密的要求有增无减。相比之下，由于量子通信有量子不可克隆定理和测不准原理的支持，安全性超过传统的通讯方式，其中，量子纠缠传输保密效果最好。本文详细介绍了量子纠缠超空间传输的2套理论方案，其中一套是建立超空间传输通道，另一套是将纠缠态传输与单量子态结合起来进行传输。

2 理论方案

2.1 第二代量子传输——量子交换（量子纠缠的超空间制造）

设实验开始前光子1、光子2处于纠缠态|Ψ-＞12，光子3、光子4处于另一纠缠态|Ψ-＞34.此时，两对光子之间并无任何纠缠，其中，光子2和光子3在Alice手中，光子1和光子4在Bob手中。这样，在Alice与Bob之间已有2条量子通道，即1～2和3～4之间的最大量子纠缠态。整个系统处于初态：

实验开始时，Alice对手中光子2和光子3做Bell态测量，产生相应纠缠分解和坍缩。这相当于用光子2和光子3的4个Bell基对这4个光子系统的上述态重新做等价的分解和展开，即：

Alice做过上述测量后，这个态将等概率随机坍缩到4项中的任何一项。比如，在某次测量中，在Alice测得的结果中，第一项为|Ψ+＞23，然后，她采取经典通信的方式告诉Bob，Bob就知道自己手中的光子1和光子4已经通过关联坍缩而纠缠起来，并已处于|Ψ+＞14态上[3]。

在此要注意的是，光子1与光子4之间并没有直接的相互作用，而是当Alice对光子2和光子3进行Bell测量时，通过光子2和光子3的纠缠，以间接方式纠缠起来的。

2.2 多个两能级粒子量子态超空间传输方案

单粒子量子态的传输可以完全或无损失地将单粒子所包含的未知量子信息从Alice处传输到Bob处的粒子上，不论Alice与Bob相距多远，只要他们之间由EPR纠缠态所关联。量子纠缠交换方案表明，2个粒子的最大纠缠形式也可以被传递，完全不相干，甚至2个远离彼此的粒子可以通过远距离操作被关联起来，而且处于最大纠缠态。我们可以考虑到把这2种方案组合起来，结合2种方案的优点，这样既能完全传递单粒子的未知量子信息，又能同时传递两粒子间的纠缠形式[4]。设传送者Alice拥有2个处于某一未知的量子纠缠态的两能级粒子，如果标明这2个粒子分别为C0，C1，则可以设C0，C1所处的量子态为：

式（1）中：系数α00，α01，α10，α11满足归一化条件|α00|2+|α01|2+|α10|2+|α11|2＝1.

实验时，先要建立传送者Alice与接受者Bob之间的量子通道。由于要传输的是两粒子的量子态，而每两粒子EPR的纠缠态形成的量子通道在使用后将会被破坏，并且利用一对两能级EPR粒子一次性地传输两粒子量子态显然是不切实际的，因此，我们考虑利用两对两能级EPR粒子形成2个量子通道来传输C0，C1两粒子的量子纠缠态。这2个量子通道分别为：

在式（2）、式（3）中，A0，A1粒子为Alice所拥有，而B0，B1粒子为Bob所拥有。在此要注意的是，这里EPR态的选取与前面有所不同，以前使用的是Bell基中的|Ψ-＞，而在这里为了方便，选取了|Φ+＞，并且凡是以后将两能级EPR作为量子通道的情况，我们将一概选取|Φ+＞，这对结果不会产生本质的影响。于是，系统ABC由2个信息粒子C0，C1及两对EPR粒子A0，B0，A1，B1所组成，其总量子态波函数为：

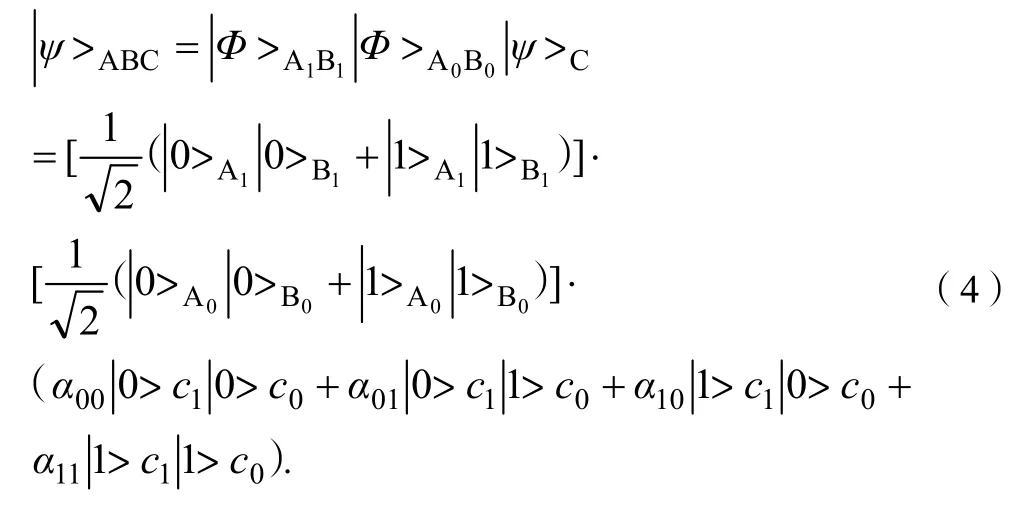
与六人方案相类似，我们可以将A0，C0粒子形成的子系统的量子态波函数按A0，C0粒子的4个Bell基展开；而A1，C1粒子形成的子系统的量子态波函数也可按A1，C1粒子的4个Bell基展开。在这里省略具体步骤，我们只写出在作完这种展开之后ABC量子系统的形式，即：

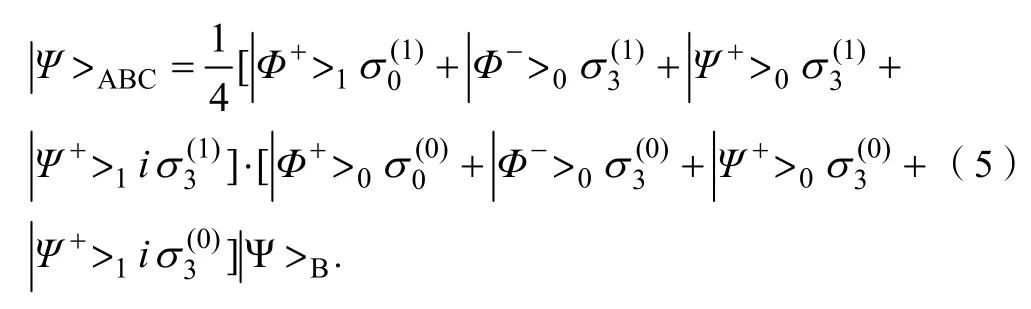
为了简化，记|＞1＝|＞A1C1，|＞0＝|＞A0C0，而所有 Pauli算符都作用于B系统，作用于B系统的对应的单粒子用上标表示。

假设接受者Bob需要用到传送者Alice手中的C0，C1粒子的纠缠态，即式（1），于是，Alice可以分别对A1，C1粒子和A0，C0粒子作Bell基的测量。每测量一次Bell基，都有可能导致两能级的两粒子的波函数以相等的概率向4个Bell基|Φ±＞或|ψ±＞之一塌缩。因此，这里测量2次Bell基，将会出现4×4＝16种塌缩结果，而每种结果出现的概率均为1/16.Alice完成对A0，C0和A1，C1的Bell基测量之后，相应的B1，B0粒子将塌缩至16种量子态之一，这16种量子态由式（2）（3）（4）（5）中每一求和项中的关于B的波函数描述。接下来，Alice将测量后A0，C0及A1，C1粒子波函数的塌缩结果通过经典通信通道告知Bob，Bob可以通过对B1，B0粒子作相应的幺正变换而使得B系统的量子态转化为：

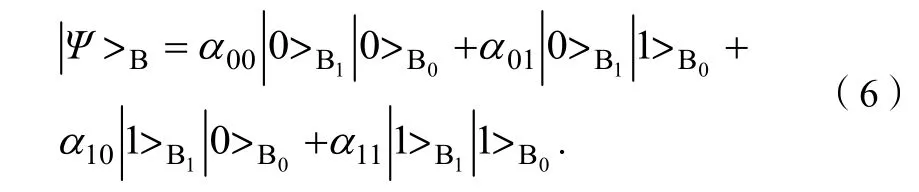
式（6）即为式（1）所描述的C系统的未知量子态，它是在Alice进行Bell基测量之前获得的。这样，2个两能级粒子未知纠缠量子态的超空间传输就完成了。

从式（2）（3）（4）（5）中可以看出，只有4种Bob对单粒子的幺正变换，即σ0，σ1，-iσ2，σ3，它们对应于 4 种Bell|Φ+＞，|Φ-＞，|ψ+＞，|ψ-＞对 B1粒子所作的 4 种幺正换，分别对应于A1，C1粒子的4种Bell基塌缩结果，对B0粒子所作的4种幺正换则分别对应于A0，C0粒子的4种Bell基塌缩结果。另外，从中可以发现，Alice对A1，C1粒子作Bell基测量对B0粒子的量子态完全没有影响，也不会导致Bob对B0粒子作幺正变换。反过来说，Alice对A0，C0粒子作Bell基测量对B1粒子的量子态也完全没有影响，也不会导致Bob对B1粒子作幺正变换。因此，我们可以采取以下的操作步骤来进行2个两能级粒子量子态的超空间传输：①传送者Alice对A1，C1粒子作Bell基测量，并将结果告知接受者Bob；②接受者Bob根据步骤①中的测量结果从σ0，σ1，-iσ2，σ3中选取相应幺正变换作用于 B1粒子上；③传送者Alice对A0，C0粒子作Bell基测量，并将结果告知接受者Bob；④接受者Bob根据步骤③中的测量结果从σ0，σ1，-iσ2，σ3中选取相应幺正变换作用于B0粒子上。采用这种步骤同样能完全传递C系统的量子态到B系统之上。

进一步了解，量子态超空间传输的理论可以推广到多个两能级粒子纠缠态的情形。我们考虑利用多个量子通道来实现这样的纠缠态的超空间传输。对于传输L个两能级粒子的纠缠态，则需要用L个两能级RPR态作为量子通道。传送者Alice将对Bell基进行L次测量，这3次测量将以相同的概率产生4L种结果中的一种。而相应的接受者Bob所需掌握的单粒子幺正变换只有4种，相对应4种Bell基。但是，由于接受者Bob需要对L个粒子作单粒子的幺正变换，而且对任何2个粒子分别所进行的单粒子幺正变换是无关联的，因此，接受者Bob需掌握的幺正变换的总的种类也是4L种，正好对应传送者Alice的4L种测量结果。