基于Markov链的隧道围岩破碎状态模拟研究

叶 亭，刘春原，李金龙，宋健康，徐良玉

（1.河北工业大学 土木与交通学院，天津 300401；2.河北省土木工程技术研究中心，天津 300401）

0 引言

地层变异性是确定隧道施工前围岩状态，选择开挖方式的主要影响因素.地质钻孔数据提供的地质信息是有限的，钻孔之间的地质体分布状态存在较大的随机不确定性，传统方法无法反映岩体的随机分布特征[1-2].Halda和Tang在1949年首次将Markov随机过程应用于沉积地层垂向叠置样式分析[3]，Rumbein和Schercr提出了采用固定步长法分析土层的转移概率，Ioannou在1984年将地层随机转移状态法用于垂直方向岩土层分析.刘振峰以Markov链为基础从转移计数矩阵入手，成功的实现沿工程纵断面方向的二维拓展[4].Elfeki在文献中讨论了利用两个离散的一维Markov链组成联合概率来模拟地层剖面的二维分布模拟的方法[5]，谢式千等将刘振峰的二维Markov链模拟方法进一步改进并应用到实际工程.刘振峰、杨长春将模拟退火算法引入Markov链模型中，在得到岩相转移概率矩阵的基础上对模拟结果进行扰动，直到得出较为满意的图像[6-7].李军在2010年将尺度数据融合的方法引入Markov预测模型中，在计算过程中协调了岩心数据和物探数据进行二维地层岩相储层模拟分析[8].然而，针对Markov链地层预测模型的研究主要是对大范围区域地层岩相组合进行模拟预测，在隧道围岩破碎状态的研究未见报道.

为此，提出了间隔钻孔数据修正的模拟方法，对钻孔数据模拟结果进行互相修正降低了地层变异不可控的风险，并将该Markov链地层预测模型应用于地质体风化破碎状态的预测.为隧道工程的设计及施工提供了有效的数据支持.

1 Markov链模拟方法原理

Markov链是1906年数学家Markov提出的“无后效性”的随机过程，即未来状态的发展与先前状态无关，只取决于现在状态.其数学表达式为

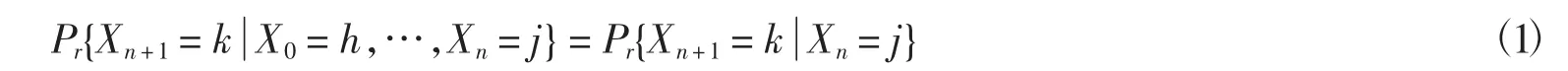
式中：X0，Xn，Xn+1为Markov随机过程中第1个，第n个以及第n+1个位置的状态；h，j，k分别为状态X0，Xn，Xn+1的取值；Pr为事件发生概率[15].

由此可以看出Markov链是有方向性的，这一特性和沉积过程的方向性相吻合，这使得利用Markov链预测地层状态成为可能[4].根据得到的地质钻孔岩芯数据，设状态空间为S{sk∈S，k=1，2，…，n}，同时假定已知地层下边界和左边界的钻孔岩心数据，右边界作为条件数据.统计计算出其相应方向上不同岩性的转移状态分布情况，求出二维空间中某位置出现sk状态的概率，见图1.网格（i，j）处出现状态Sk的概率计算公式见式（2）

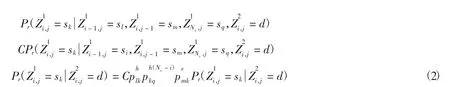
式中：用上标表示模拟随机域，1为小尺度模拟随机域即钻孔岩芯统计域，2为大尺度模拟随机域即物探数据统计域；d为大尺度网格状态（根据物探波速统计的岩性状态）；h为垂直方向，v为水平方向；i，j分别为状态模拟网格的位置；Nx为条件网格位置；sl，sm分别为水平向、垂向已知状态；sq为条件状态；C为归一化参数[5]；Pr为概率.

在参数修正过程中可以利用高斯转换模型进行统计域之间数据的转换[8]，具体转换公式见式（3）.

其中：φ（x），φ（x）代表不同尺度数据之间的概率融合转换映射过程；ml代表一个待模拟大尺度场中的小网格数；ε～N（μ，σ2）为准确度控制函数，在地质统计学中一般用正态分布，其中均值μ及方差σ2根据待模拟区域物探统计数据得出；xl，xs为不同尺度网格取值.

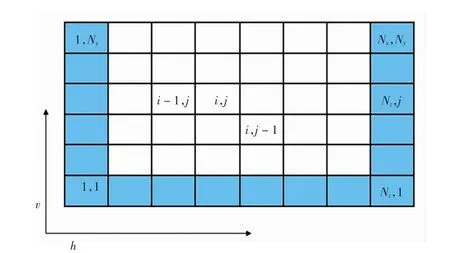
图1 条件二维Markov链网格模拟计算示例图Fig.1 The example of two-dimensional Markov chain mesh simulation

2 Markov链围岩剖面模型的建立

用Markov链模型进行模拟的过程中，利用已知钻孔实测数据，将区域岩层的破碎状态分布统计规律[14]转化为随机转移状态矩阵，采用间隔钻孔信息修正的方法，进行模拟计算，具体步骤如下：

1）对待模拟区根据地形条件及钻孔数量进行区域网格划分；

2） 选取符合条件的3个相邻钻孔，编号Y1，Y2，Y3，经χ2检验符合Markov条件后，将Y1钻孔岩芯破碎状态数据转化为区域随机转移状态矩阵，Y3号孔作为条件数据，进行随机模拟计算，如图2所示；

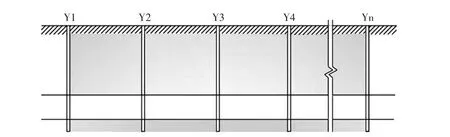
图2 间隔钻孔数据修正Markov隧道围岩破碎带分布预测示意图Fig.2 Sketch map of the distribution of the surrounding rock broken zone in the Markov tunnel with interval data

3）对计算结果应用Monte-Carlo法进行大量次的随机模拟赋值，形成Y1～Y3区域多个Monte-Carlo模拟图像；

4）提取模拟结果虚拟Y2孔数据，并与真实Y2孔数据进行对比分析统计吻合率，选取吻合度最高的实现结果作为修正图像；

5）将Y2孔作为原始数据，下一钻孔作为条件数据进行递进模拟实现，得到Y2～Y4区域模拟图像，通过对比计算虚拟Y3孔与真实Y3孔的模拟结果，选取模拟效果最高的图像；

6）结合两次最优模拟结果对重叠区进行数据修正，依次进行得到实验区完整的模拟图像.

通过间隔钻孔数据依次递进计算，互相修正，减小地层变异性对围岩破碎带转移状态的影响，得到更为真实可靠的围岩破碎带分布数据.

3 隧道围岩破碎带模拟分析

3.1 工程概况

张石高速某隧道工程项目隧址区位于河北省保定市太行山中部山区，勘测路线起于涞源县孤山北至紫荆关北.除局部缓坡及沟谷处堆积第四系全新统坡崩积层及坡洪积层外，大部分地段基岩裸露.模拟区RK73+450～RK77+450里程段地层岩性为燕山期花岗侵入岩，风化破碎程度不均，节理较发育，未发现断层.

3.2 转移状态矩阵建立

首先选择标高为600～700 m，里程RK73+450～R K77+450为模拟区段，选取其中9个钻孔（ZKSD12-3～ZKSD12-14号）岩芯数据.取垂直方向步长为1 m，水平方向步长为5 m，模拟剖面为100×200的矩形模拟系统进行模拟计算.按层序生长方向对钻孔进行岩芯破碎状态进行转移记数统计，采用χ2检验法对Markov性进行检验.统计结果为：垂向向下χ2=98.437 5，垂向向上χ2=96.876 2，其值均大于置信度为0.014χ2分布的临界值χ20.014=13.277.由此可知该区域围岩破碎分布序列具有较强的Markov性[9]，可以带入随机预测模型进行围岩破碎带转移状态的模拟预测.

按照Markov链模型对水平向岩相的转移记数矩阵进行计算.从地震剖面上测得了层序不同方向上的倾角θ为14.5°并计算该区域的侧向的延伸度之比14.5°倾角余切为3.866 7，得到水平向转移概率矩阵[7]，统计计算的不同方向岩芯破碎状态序列的转移记数矩阵和转移概率矩阵如表1所示.

3.3 物探数据统计修正

统计物探数据，以地震剖面划分不同波速区间根据测井、岩芯资料统计得到不同波速区间的隧道围岩破碎带出现的概率分布，其地震纵波统计概率分布见图3.统计并计算地震剖面图不同尺度融合的精度控制函数ε～N（0.45，1.42），将物探数据带入高斯分布随作为约束条件，加入到条件化二维Markov链模型中[8，12-13].使用Matlab数据处理软件经过数学编程，进行里程K46+625～K47+225区段隧道围岩破碎带模拟建模.

3.4 围岩破碎带模拟结果分析

Markov模拟网格区域垂向选取标高600～700 m，纵向选取里程RK73+450～RK77+450进行网格划分然后沿隧道走向分区段进行，结果见图4.其中a） 为里程段RK73+450～RK74+450，b） 为里程段RK74+450～RK75+450，c） 为里程段 RK75+450～RK76+450，d） 为里程段 RK76+450～RK77+450，由模拟图像所反映出的围岩破碎带分布的区域性及连续性特征与根据钻孔资料和地质超前预报资料分析得出的隧道围岩破碎带分布规律是一致的.对比隧道勘察数据，该区模拟准确率80.7%～89.6%.

由模拟图a） 看出，在隧道孔顶标高635 m，孔低标高623 m.隧道垂直孔径12 m，隧道在进口里程RK73+450处穿越中风化围岩区，在里程RK73+950处开始围岩破碎程度出现较大改变，其中在里程RK73+900～RK74+030区段隧道围岩孔顶上方标高626～635 m，预测出大片中风化较破碎花岗岩.此处按照设计勘察报告为II级围岩，围岩完整性较好.

图3 不同波速（纵波）区间各岩石破碎带出现的概率条形统计图Fig.3 The probability bar graph of each rock fracture zone with different wave velocity

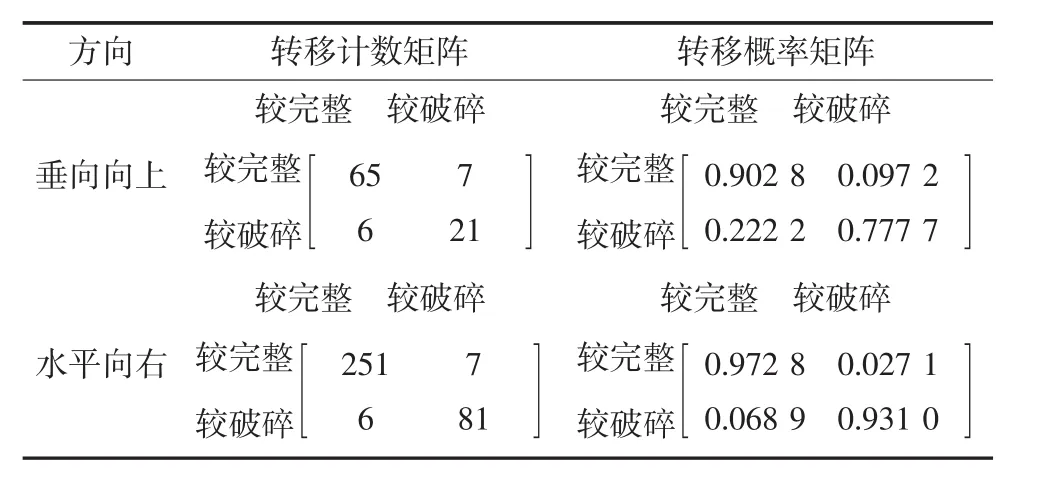
表1 不同方向围岩破碎带转移记数矩阵及相应的转移概率矩阵Tab.1 Different directions surrounding rock with transfer count matrix and corresponding transtion-probablity matrix

图4 RK76+450～RK77+450区段隧道围岩破碎区模拟结果Fig.4 Simulation results of RK76+450～RK77+450 section tunnel surrounding rock broken zone

结合施工日志及隧道工程变更通知，在里程RK73+998～RK74+018区段发生隧道洞顶碎石塌落，围岩由原设计II级改为Ⅲ级，该模型更准确的实现了隧道围岩状态模拟预测预报.

由模拟图c） 可以看出模拟里程RK75+450～RK76+450区段，在里程RK75+800至RK76+050处隧道开始穿越围岩中风化破碎区，且该区围岩在标高618～642 m区域多处出现水平连续性花岗岩破碎带，围岩极不稳定.该区地质勘察报告设计为II级微风化花岗岩，围岩较稳定.这是由于传统地质剖面在里程RK75+560处勘测结果存在盲区.工程实例证明，通过围岩分布模拟预测模型实现了隧道围岩破碎带有效的预测，修正了初始隧道围岩地质剖面图，解决了现有隧道地质勘测方法存在盲区的问题.该模型为隧道综合风险评价提供了数据支持，对于隧道安全建设具有重要意义.

4 结论

张石高速隧道工程围岩模拟预测的应用实例表明，对于采用间隔钻孔数据修正的Markov链模型进行隧道围岩破碎带的模拟预测是可行的，可以反映隧道围岩展布特征.主要结论如下：

1）通过间隔钻孔数据依次递进计算，互相修正，可以减小地层变异性对地层岩性转移状态的影响，得到更为真实可靠的岩性分布数据.

2）采用间隔钻孔数据修正的Markov链模型进行二维隧道围岩破碎带随机模拟，结合隧道开挖掌子面施工日志资料，预测准确率达80.7%～89.6%.

3）应用改进的Markov链模型进行围岩破碎带模拟，可以修正隧道围岩地质剖面图，解决了现有隧道地质勘测方法存在盲区的问题.

[1] 王仁铱，胡光道.线形地质统计学[M].北京：地质出版社，1988.

[2]Yarus J M，Chambers R L.随机建模和地质统计学—原理、方法和实例研究[M].穆龙新，陈亮，译.北京：石油工业出版社，2000.

[3]Schwarzacher W.沉积模型和定量地层学[M].徐桂荣，译.北京：地质出版社，1984.

[4] 刘振峰，郝天珧，杨长春.基于链模型的储层岩相随机模拟[J].地球物理学进展，2003，18（4）：666-669.

[5] Elfeki A，Dekking A.Markov chain model for subsurface characterization[J].Theory and applications of Mathematical Geology，2001，33（5）：568-589.

[6] 刘振峰，郝天珧，杨长春.沉积模型和储层随机建模[J].地球物理学进展，2003，18（3）：519-523.

[7] 刘振峰，郝天珧，方辉.用链模型随机模拟储层岩相空间展布[J].石油学报，2005，26（5）：57-60.

[8] 李军，熊利平，方石，等.基于多尺度数据融合Markov链模型的岩性随机模拟[J].石油学报，2010，31（1）：74-77.

[9] 刘振峰．基于MRF模型的油气储层属性随机建模方法研究[D].北京：中国科学院研究生院，2004.

[10]Haldar A，Tang W H.Uneorminty analysis of relative density[J].Journal of Gentechnical Engineering ASCE，1979，110（4）：525-530.

[11]Norberg T，Rosen L，Baran A.On modeling discrete geological structures as Markov random fields[J].Mathematical Geology，2002，34（1）：63-77.

[12]沈洪涛，郭乃川.地质统计学反演技术在超薄储层预测中的应用[J].地球物理学进展，2017，32（1）：248-253.

[13]侯斌，陈波，薄永德，等.基于地质统计学反演的薄互砂岩储层预测[J].复杂油气藏，2016，9（4）：12-15.

[14]王宇.基于岩性分析的公路隧道围岩动态分级研究[D].长沙：长沙理工大学，2015.

[15]孙安黎，杨阳，伍焓熙，等.基于马尔可夫过程的项目风险评价方法的研究[J].理论与算法，2016，24（1）：36-37.