基于PCNN的图像最佳二值分割实现
2018-01-30苏彦莽高振斌
白 明,王 莉,苏彦莽,高振斌
0 引言
商品的赋码是我国政府部门以及市场监管部门对消费品的一种电子监管手段,其方法就是赋予每一件商品一个监管码[1-3].随着商品数量的不断增多及种类的不断更新,各行各业都开始使用赋码监管系统,一方面可以使消费者充分了解商品,另一方面也符合国家电子安全监管的理念[4].因此,对监管码识别准确率要求相对较高,而字符图像二值分割的好坏对监管码的识别起着决定性的作用.
根据数字图像的特征分布情况不同、图像各自的特性不同及对图像兴趣区域的限制条件不同,将兴趣区域从目标图像的背景中分割出来的方法、理论也多种多样.几种常见的分割方法有:边缘检测分割方法、OSTU分割方法、固定特值分割方法等.
文献 [5]使用OSTU方法对图像进行分割,该方法实现相对简单,且分割效果好,但是无法实现图像中各区域的自适应分割.
生物学家在研究哺乳类动物的视觉皮层时发现,在某一种外部刺激下哺乳类动物的一片特定部分能够激发脉冲信号,这些特定的部分有着相似的特性,根据这种脉冲耦合特性建立了PCNN模型.随着PCNN网络研究逐渐深入,他的性能也更完善,其最主要的特点是:具有记忆功能、网络容量大、高效的计算能力.PCNN网络内部每个神经元都存储着部分信息,在信息处理的过程中,所有神经元处于并行处理的状态.此外,人工神经网络有着超强自学习能力,通过学习和适应改变内部参数和结构可以达到近似任何函数的效果,因此广泛用于数字图像处理领域.
PCNN网络在图像的二值分割中,所获得的结果除了受网络参数的影响还与网络的迭代次数有关.因此,本文采用图像的交叉熵最小理论控制迭代次数,来实现算法的自行分割图像[6-8].
1 改进的PCNN分割方法
1.1 PCNN神经元模型及工作原理
PCNN网络神经元模型如图1所示.
PCNN网络整体工作流程可以大致表示为:
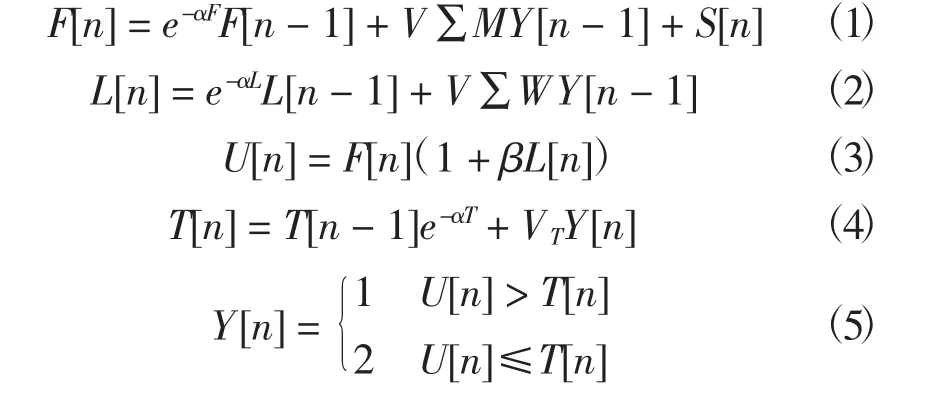

图1 PCNN网络神经元基本模型Fig.1 Basic model of PCNN neural network
式中:F[n]是对应神经元的反馈输入,S[n]是图像中对应像素的灰度值;M和W为当前神经元的连结权值矩阵,即卷积核,它代表当前神经元与相邻神经元之间互相作用的程度;V表示神经元固有电平;VT表示神经元固有门限电平;β表示神经元相互影响作用程度;Y表示当前神经元输出脉冲信号,定义Y=0时,神经元被抑制,此时无脉冲信号产生,当Y=1时,神经元被激活,此时产生脉冲信号;T表示当前神经元能否产生激发脉冲的动态电平阈值.
PCNN内部由许多神经元构成,在数字图像处理中,主要利用其激发脉冲的同步特性以及邻近神经元捕获特性.图2为PCNN处理图像的过程.
1.2 最佳分割方法的确定
熵是用来衡量事件中不确定性信息大小的一个量.交叉熵是表示2个不同概率分布的熵的差异.设有2个信息集合,其概率分布分别为P、Q,其公式可表示为

式中:D(P∶Q)为集合P与Q的交叉熵;pi为集合P的概率元素;qi为集合Q的概率元素.
直接运用PCNN网络分割图像,无法准确判定具体哪一次点火图像为最佳二值分割图像,只能通过对实验数据的大量统计得出.这种结论往往受其他因素的干扰而不准确.本文采用最小交叉熵原理优化PCNN网络迭代次数,其流程如图3所示.在图像分割过程中,P,Q分别表示目标图像和分割后图像的分布情况.当二者交叉熵D最小时,该分割后的图像信息与原图像信息最为接近,判定此时分割效果最好.
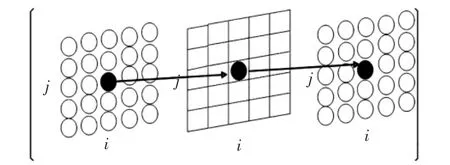
图2 图像处理过程Fig.2 Image processing
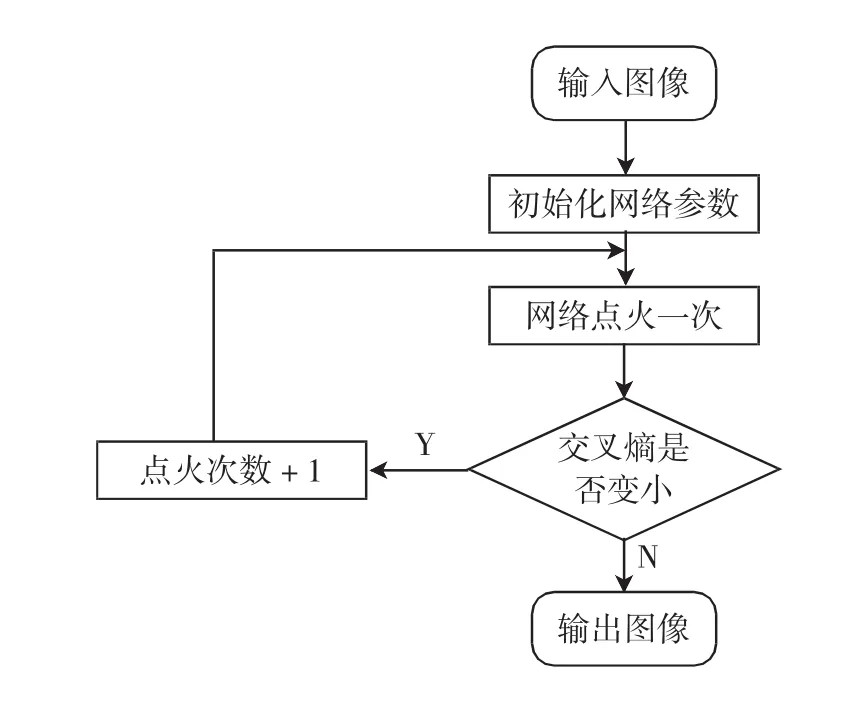
图3 最佳二值分割方法Fig.3 Optimal two value segmentation method
2 图像二值分割的FPGA实现
2.1 PCNN模块设计
2.1.1 设计对象
在使用MATLAB计算PCNN网络过程中,主要对象设计如表1所示.
网络运算过程中,主要是更新输入反馈项F、线性输入项L、动态阈值T以及脉冲输出Y.通过反复更新这些值,就能够得到一个完整的时间序列.主要有6个变量和8个常量需要存储.6个变量分别为K、L、U、Theta、Y、F,其存储的大小与待处理图像相同.8个常量分别为alpha_L,alpha_Theta,alpha_F,beta,W,vL,vF,vT.在计算的过程中,因为exp(-alpha_L),exp(-alpha_Theta),exp(-alpha_F)亦为常数,所以为了减少运算量,提前计算其结果并将其整体存储.W为连结矩阵,是影响连接域的关键,vL、vF、vT分别为L、F以及Theta的初始固定电平,DM为原始图像.
2.1.2 数据表示方法
在神经网络计算的过程中,因为阈值vTheta一般相对较大,故采用16位二进制数据表示,其他常量均用8位二进制数据表示,与待处理图像的像素位宽相同.但是在计算时,为了提高网络运算精度,将变量K、L用16位二进制数据表示,其中小数位和整数位各8位.变量U、T、F变量用24位二进制数据表示,其中小数位为8位,整数位为16位.
2.1.3 模块设计
在PCNN网络的实现中,存储模块将所需参数以及中间部分运算结果储存起来,运算模块将输入的数据计算后在控制模块的操作下完成与存储单元之间的数据交换.整体设计电路如图4所示.
运算模块主要包括卷积模块和线性计算模块.卷积模块主要为了计算变量K,可以利用3个RAM以及2个计数器完成.如图5所示,3个RAM是用来缓存图像的3行数据.计数器1控制RAM地址信号,计数器2控制运算的行数.
线性计算模块主要是计算变量线性输入项L、反馈项F以及动态门限Theta.以L计算模块为例,如图6,其它类似.
存储模块主要由RAM构成:图像数据RAM_X、线性项RAM_L、内部活动项 RAM_U、点火输出RAM_Y、动态阈值RAM_TH.当写使能有效时(写使能高有效),向addr处写入数据.地址线深度为15 bit,ram容量256×128;数据线宽度RAM_X为8bit、RAM_L为16 bit(8 bit小数位)、RAM_U为24 bit(8 bit小数位)、RAM_Y为8 bit、RAM_TH为24 bit(8 bit小数位) .
控制模块主要是由计数器和状态机组成,通过输出使能信号来控制运算模块内所有变量的计算、更新以及运算模块和存储模块之间的数据流动.其内部结构如图7所示.

表1 PCNN算法的主要计算模块Tab.1 The main computational blocks of PCNN algorithm

图4 PCNN整体结构Fig.4 Overall structure of PCNN
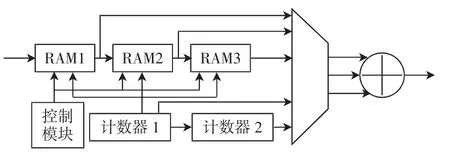
图5 卷积模块内部结构Fig.5 Internal structure of convolution module

图6 变量L的计算过程Fig.6 Calculation process of variable L
状态机主要有空闲Idle状态、初始化Init状态、计算L Calc_L状态、等待L Wait_C_L状态、计算U Calc_U状态、计算Y Calc_Y状态、计算Theta Calc_Th状态.
状态机工作流程为:
Idle:当rst信号有效时令状态机为Idle复位状态,所有变量复位,rst拉高后待写使能有效跳转至Init;
Init:初始化状态,初始化RAM_X(灰度),RAM_Y(全0),RAM_L,RAM_U和阈值Th,将迭代次数初始化为0,当写使能拉低跳转至Calc_L;
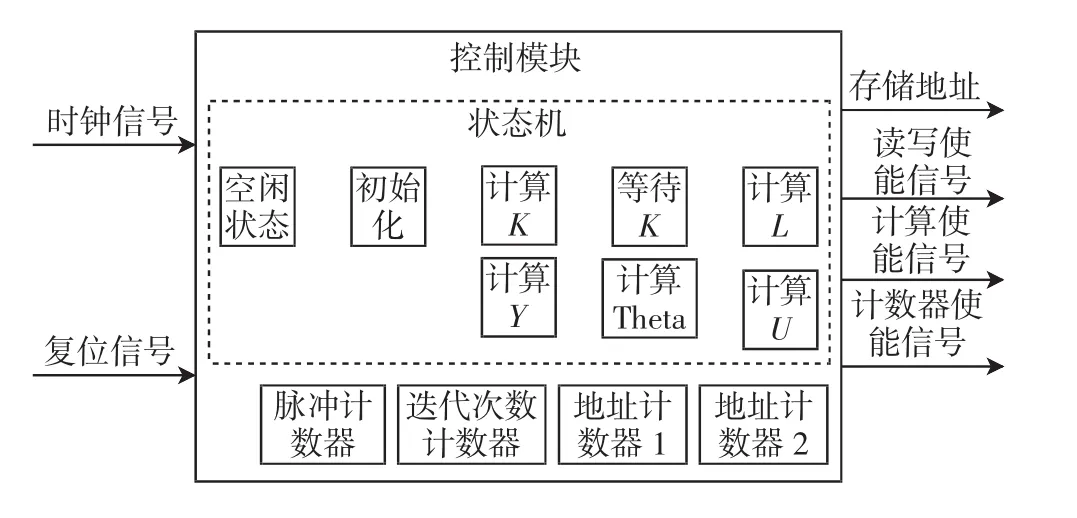
图7 控制模块的结构Fig.7 Structure of control module
Calc_L:将X、Y矩阵输入conv模块计算L矩阵;Y矩阵读完后跳转至Wait_C_L;
Wait_C_L:等待L矩阵计算完毕,计算完毕后跳转至Calc_U;
Calc_U:计算U矩阵,待U计算完毕后跳转至Calc_Y;
Calc_Y:将U矩阵与阈值Theta进行比较,更新Y矩阵,并将Y矩阵输出至最小交叉熵计算模块,矩阵更新完毕后跳转至Calc_Theta;
Calc_Theta:更新阈值Theta,计算完毕后跳转至Idle;
迭代次数计数器主要负责控制整个图像被PCNN网络处理的次数以及各个变量的更新状态.当该计数器等于预先设定值时,网络计算终止,状态机回到Idle状态.
2.2 图像的二值分割模块
在图8中,初始化模块将PCNN网络的初始化参数与原始图像数据传入PCNN模块,该模块主要功能是完成分割图像的迭代运算,并将更新的阈值、生成的二值图像以及记录点火情况的标志矩阵存入RAM中.RAM模块将生成的点火图像和原始图像传递至最小交叉熵模块中.最小交叉熵模块通过使能信号控制PCNN模块的迭代.直至第n+1次迭代运算后,最小交叉熵模块判断此次迭代后的分割图像的交叉熵大于第n次的值,此时,第n次交叉熵为最小交叉熵,即判定第n次分割图像为最佳分割图像.
交叉熵计算模块主要由乘法器、加法器、除法器以及对数计算模块组成,如图9所示.对数计算模块是由一个Block RAM构成.利用查找表的方式来计算对数.其输入由八位小数和八位整数组成,查找表数据由MATLAB生成.

图8 图像的分割模块Fig.8 Image segmentation module

图9 熵计算模块Fig.9 Entropy calculation module
3 结果及分析
为了说明改进后的效果,本文首先对比了PCNN网络直接分割图像时,不同迭代次数的图像分割效果,然后对比了OSTU算法的分割效果.
3.1MATLAB实验结果
图10为原始图像以及PCNN网络直接分割图像时第4~8次的点火图像.其中可以看到PCNN网络迭代到第7次时,图像分割效果最好.

图10 PCNN直接分割图像Fig.10 Direct segmentation of PCNN
图11中为本文算法和OSTU算法在处理灰度图像时的效果.通过对比显示,待处理图像中字符特征相对比较明显时,二者差距不大;当背景颜色较深或者图像中字符特征相对较弱时,本文算法处理效果更加优越.
3.2 FPGA实现结果
本文设计可处理8位的256*128灰度图像.设计采用Zedboard开发板,其核心芯片为Xilinx公司的ZynqTM-7000,内部有大小为36Kb的Block RAM存储资源.外部时钟为100MHz,且接口资源和IP核资源丰富.实验对象为图10中原始图像.
3.2.1 PCNN分割模块
data_in为模块输入数据,data_out为计算图像数据X和点火后矩阵Y的卷积结果,nstate代表当前状态机状态,data_y为本次迭代后的点火图像数据.当nstate为cal_l时,计算线性项L,计算完成后状态机跳转为cal_u状态,计算内部应激项U,以此类推,如图12所示.

图11 不同算法的二值分割效果Fig.11 Two value segmentation results of different algorithms

图12 PCNN模块仿真图Fig.12 Simulation of PCNN module
3.2.2 对数求解模块
clk为时钟信号,信号a为图像前景各级灰度值,信号b为图像前景平均灰度值,信号c表示abs(a*log10(a/b)),信号sign为信号c的计算符号:‘1’为正,‘0’为负,对数计算结果如图13所示.
3.2.3 最小交叉熵模块
h1为背景像素点数,h2为前景像素点数,g1为背景灰度总值,g2为前景灰度总值,data_X为输入的灰度图像数据,data_Y为分割后的二值图像,D为计算后的交叉熵.sig_c和sign信号由对数求解模块输出.当sign=1时,sig_c加到d_temp中;当sign=0时,d_temp减去sig_c.最终结果输出交叉熵D,如图14所示.将计算后的交叉熵数据导出到MATLAB中显示,图像第7次分割后,其与原始图像交叉熵最小,如图15所示.

图13 对数求解模块仿真图Fig.13 Simulation of logarithmic solution module

图14 交叉熵计算模块仿真图Fig.14 Simulation of cross entropy calculation module
4 结束语
常规二值分割方法及PCNN网络直接分割图像的方法受网络参数的影响,本文设计的联合最小交叉熵理论的PCNN分割方法可以有效的解决这个问题.MATLAB实验结果表明本文的设计方法在分割时比常规方法的效果更好,并能实现PCNN网络自动分割图像.Modelsim仿真的结果证明了本文设计方法在FPGA上的可实现性.

图15 交叉熵计算结果Fig.15 The result of cross entropy calculation
[1] 蒋井明,李萱津,王榕榕.药品电子监管码在赋码过程中的常见问题与处理[J].机电信息,2010(5):50-53.
[2] 彭秉军.奶粉行业产品质量全程追溯系统研究与实现[D].长春:吉林大学,2015.
[3] 王小芳,张鹏飞,仝丽梅.“电子监管码”知多少[J].印刷世界,2012(11):27-29.
[4] 刘祥.移动互联时代“互联网+产品质量追溯”管理体系建立初探[J].标准科学,2016(4):81-84.
[5] 孙玉梅,王鹏遥,孙巧妍,等.轮胎胎面参数在线检测系统研究及应用[J].仪器仪表学报,2016,37(12):2859-2865.
[6] 徐黎明,吕继东.基于最小交叉熵的改进PCNN杨梅图像分割算法[J].西北师范大学学报(自然科学版),2016,52(1):43-46.
[7] 沈艳,张晓明,韩凯歌,等.PCNN图像分割技术研究[J].现代电子技术,2014,37(2):38-41.
[8] DENG,Xiangyu,Yide.PCNN model analysis and its automatic parameters determination in image segmentation and edge detection[J].Chinese Journal of Electronics,2014,23(1):97-103.
