基于NSGA-Ⅱ算法的爬楼轮椅座椅调节机构多目标优化
2018-01-30范柳彬曹东兴鲁建军贾利想
范柳彬,曹东兴,鲁建军,贾利想,李 灿
(河北工业大学 机械工程学院,天津 300130)
考虑到现有普通轮椅不具有越障性能,爬坡能力也明显不足,给其应用带来了不少限制.在实际生活中存在着不少的楼梯障碍,特别是在社会经济水平不发达地区,无障碍设施建设比较落后,轮椅的使用范围受到很大的限制[1].随着我国正在进入老龄化社会和残疾人士的逐渐增多,人们对于智能轮椅的需求越来越迫切,因此社会普遍呼吁一款功能更加全面的轮椅能尽早推向市场.针对这种情况,设计一款物美价廉、方便灵活、安全可靠、经久耐用、适应不同功能和需求的爬楼梯轮椅具有重大的现实意义和实用价值[2].爬楼轮椅的研究主要分为机械部分和控制部分,本文主要研究爬楼轮椅的座椅姿态调节机构,其是一种应用于爬楼轮椅上调节座椅和使用者重心位置的调节系统,该系统不仅直接影响爬楼过程中整机的稳定性,还影响着使用者的舒适性;其本质为一交叉四连杆机构,作为爬楼轮椅的重要组成部分,对该机构有着严格要求即运动平稳性、工作空间、所需驱动力矩大小.然而机构中杆件尺寸直接影响着上述性能,因此有必要对交叉四杆机构进行优化设计.本文通过对座椅调节机构进行运动学和动态静力学分析,确定了机构各尺寸参数与其工作空间即工作性能指标、运动平稳性即舒适性能指标、驱动力矩即力矩性能指标之间的函数关系,从而建立了关于机构尺寸参数的多目标优化数学模型,并且采用NSGA-Ⅱ遗传算法得到了Pareto最优解,然后为满足机构不同的使用要求在Pareto最优解中选取最优尺寸参数,设计了5组方案.由于本文主要侧重使用者的舒适性能,故选取舒适性能达到最优情况下的数据进行仿真,进而去比较优化前后各性能指标的变化从而去验证设计的合理性和准确性.
1 运动学求解
1.1 角位移分析
座椅姿态调节机构可以简化为图1所示的两自由度交叉四杆机构,其中连杆JH代表座椅.通过电机驱动丝杠使滑块移动进而使δ发生变化从而调节座椅姿态,即已知δ及滑块的运动规律,其姿态形式分为2种情况,若θ2≥180°时处于前倾阶段;反之处于后倾阶段运动.由封闭矢量法可知

沿x、y轴投影可得

图1 座椅姿态调节机构模型Fig.1 Seat position adjusting mechanism model

式中:θ1为连杆AH与x轴正向夹角;θ2为连杆JH与x轴正向夹角且θ2=π+θ1-δ;θ3为连杆BJ与x轴正向夹角.解得
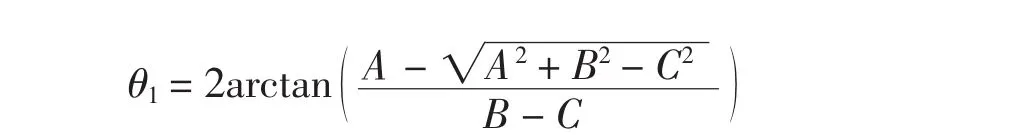
1.2 角速度分析
将式(1) 对时间t求导,可得
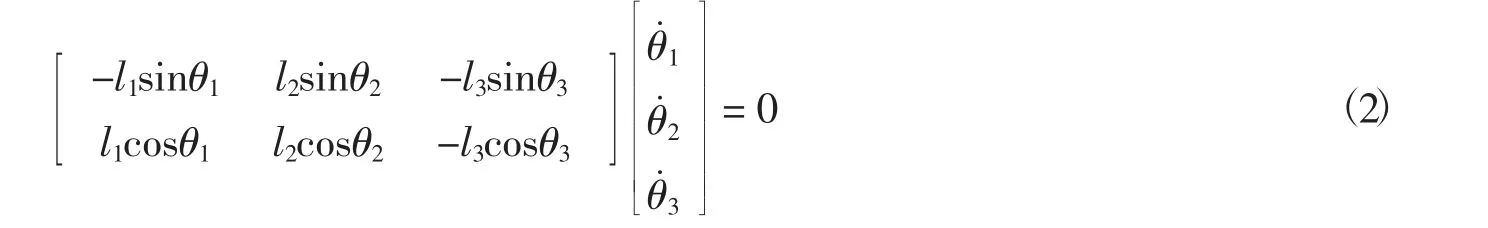
1.3 角加速度分析
将式(2) 对时间t求导,可得
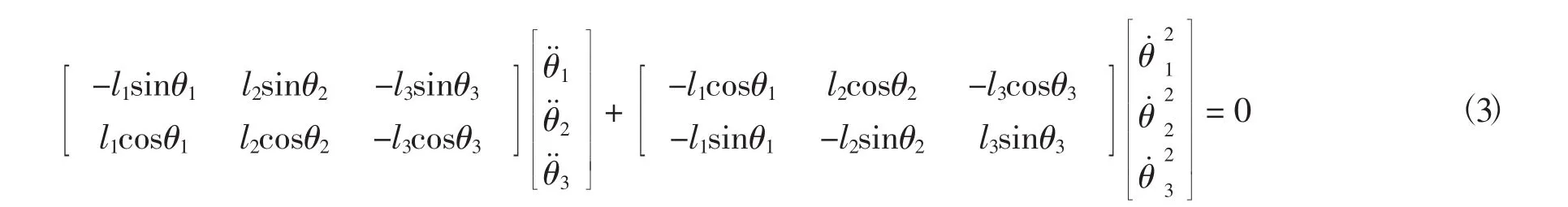
1.4 连杆JH质心加速度分析
由式(1)、式(2)、式(3) 可得,连杆JH质心加速度如下
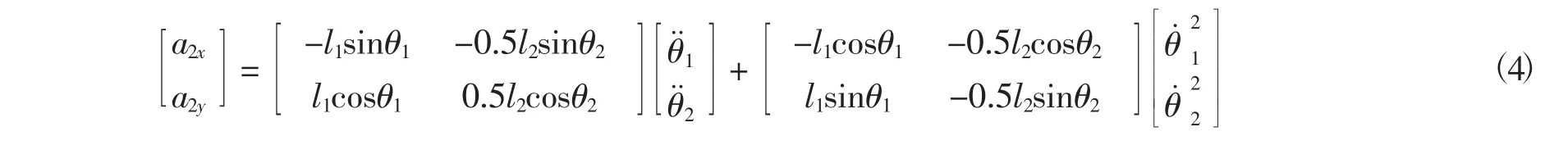
2 动态静力学受力分析
为方便对座椅姿态调节机构进行受力分析,现做如下假设:
1)由于座椅和使用者绝大部分的重量都集中在连杆JH上,故在对座椅姿态调节机构进行受力分析时,仅研究连杆JH受力情况且连杆JH为均质杆且忽略其他杆质量;
2)假定认为使用者和连杆JH质量均集中连杆质心处.
其受力示意图如图2所示.

图2 座椅受力分析简图Fig.2 Seat force analysis diagram
可将各杆件受力平衡方程写成矩阵形式,如下:

式中:A、X、B分别为系数矩阵、未知量矩阵、已知量矩阵,且有

式中:FAx、FAy为铰点A处受力;FHx、FHy为铰点H处受力;FBx、FBy为铰点B处受力;FJx、FJy为铰点J处受力;f1、f2为滑块所受摩擦力;F2x、F2y为座椅所受惯性力;M为座椅驱动力矩;M*为座椅所受惯性力矩.
系数矩阵 A=[A(i,j)]11×11,其中非零元素为

由以上分析可知各未知力为

故当座椅动作时连杆JH质心处所受合外力矩M2为

3 座椅姿态调节机构优化设计数学模型
3.1 设计变量
由于在交叉四杆机构中连杆1和连杆3长度相同,因此选取连杆1和连杆4为独立设计参数,即:

3.2 确定约束条件
对于交叉四杆机构不仅需要综合考虑机构运动干涉情况、四连杆机构成立条件,还需要保证座椅动作时良好的工作空间,这样方可建立交叉四杆机构的约束条件,其建立过程如下:
1)为了保证交叉四杆机构可以正常动作,即保证连杆1为曲柄,建立如下约束条件

2)交叉四连杆机构运动不干涉的条件

3)为了保证机构的正常传动,即交叉四杆机构要满足传动性能约束条件

4)设计变量的边界约束条件

5)由于座椅姿态调节机构包括前倾阶段和后倾阶段,并且2个工作阶段的工作空间呈现对称的特点,同时为了保证座椅具有较大的调节空间,即保证座椅具有良好的工作性能,选取后倾阶段为例建立其约束条件

3.3 确定目标函数
3.3.1 工作性能指标
为了适应不同环境和人群的使用需要保证座椅姿态调节具有较大的工作空间,根据此设计要求将工作空间作为其工作性能的评价指标.当座椅动作时铰点H、J之间纵坐标产生位移差,差值的绝对值大小与工作空间呈现正相关性,故该子目标的目标函数由式(1)可得

式中:yH为H铰点纵坐标且yH=l1sinθ1;yJ为J铰点纵坐标且yJ=l3sinθ3.
3.3.2 舒适性能指标
考虑使用者的舒适性则需要保证座椅姿态调节启动瞬时及其动作过程中质心所受加速度要尽可能的小,以防使用者身体出现剧烈的晃动,在此选择连杆JH质心处的加速度作为优化目标,其子目标函数由式(4) 可得

3.3.3 力矩性能指标
伺服电机的力矩性能[3]是限制爬楼轮椅座椅姿态调节机构动作的一项重要因素.在选择电机型号时,必须保证所选电机峰值扭矩大于座椅负载的峰值扭矩,因此在相同条件,选取与之相对应的质量较小的电机,有利于降低整个机构的重量,从而提高其续航能力.另外,考虑到座椅的灵活可靠性,也需要保证座椅在动作时所需驱动力矩较小,这样也可间接保证交叉四杆机构上铰接处点受力变小,从而减少了连杆的磨损,提高了座椅的使用寿命,在此选择连杆JH质心驱动合力矩作为优化目标,其子目标函数由式(6)可得:

基于上述确定的约束条件和目标函数,建立了座椅姿态调节机构的多目标优化模型,如下:

4 基于NSGA-Ⅱ算法优化结果分析
本文采用基于Pareto解的NSGA-Ⅱ算法进行求解,它是一种精英策略非支配排序遗传算法[4-5],故使用该算法对所提出的多目标优化问题进行求解.另外在多目标优化问题中,由于各个子目标在优化过程中相互矛盾,不可能同时使各子目标达到最优,所以优化结果通常为1个解集.求解多目标优化问题的主要任务是:毫无偏好的找到尽可能多的具有代表性的符合要求的Pareto解,然后根据设计要求和工程实际经验,从中客观地选择最满意的优化结果[6].
4.1 NSGA-Ⅱ算法流程
1)采用实数编码:采用实数编码,1个实数值对应1个等位基因;
2)初始值赋给:将给定的各个设计变量的初始值转化为0~1之间的数,之后由随机函数产生初始值;
3)适应度函数:对种群进行非支配排序过程中,为每一个非支配层给定了虚拟适应度值,使得算法以最快速度收敛于最优区域;
4)遗传算子:选择算子采用轮赛制选择算子,即选择2个个体,首先比较非支配排序序号,选取较小的个体,若非支配排序序号一样,比较个体拥挤距离,选取较大的个体,交叉算子采用二进制交叉算子,编译算子采用多项式变异算子;
5) 运行参数设置:取种群大小500,变异概率0.1,交叉概率0.9,运行代数500代.
4.2 优化仿真结果分析
由NSGA-Ⅱ遗传算法得到得到了Pareto最优解,如图3所示,横坐标均为力矩性能指标的实际函数值,纵坐标分别为舒适性能指标、工作性能指标的两子目标实际函数值.可以看到力矩性能指标与舒适性能指标保持一种相互冲突的关系,即一个性能的提高必然导致另一个性能的下降;而力矩性能指标与工作性能指标之间呈正相关的特点,即一个子目标的增大或减小同时导致另一个子目标的增大或减小[7].

图3 Pareto最优集中优化性能指标的占优关系在二维空间上的映射Fig.3 Pareto optimal centralized optimization performance index of the dominant relationship in two-dimensional space mapping
本文已将原设计点位置标记在图3a)、图3b)上,可以看到原设计点位置虽然保证了力矩性能指标较为合理,但其余指标值却偏大,并没有兼顾到另外两子目标的平衡性;然而Pareto最优解可以为设计人员提供多种选择方案,本文分别在图3中提取各子目标最小函数值的位置点,又由于力矩性能指标与工作性能指标具有正相关性,因此提取2个位置点,同时需要考虑到所选位置点要兼顾各个子目标性能,故再选取上述附近的3个位置点进行比较分析,由表1可知:如果想要追求更好的力矩性能和工作性能,可以选择方案1;如果想要追求更好的舒适性能,可以选择方案2;如果想要兼顾3个子目标的性能平衡性,可以选择方案3.
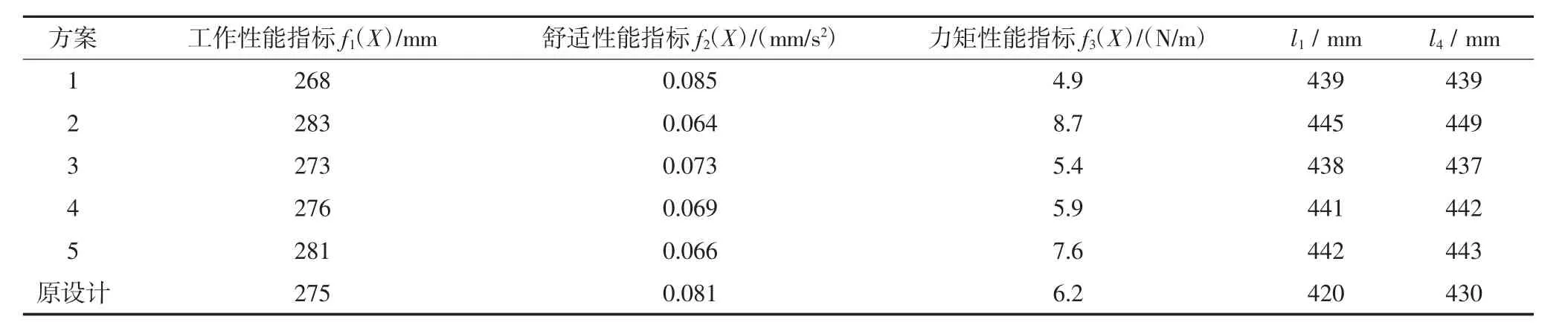
表1 优化性能指标与相关设计变量Tab.1 Optimizayion peformance index and the related dedign
4.3 优化前后仿真验证
爬楼轮椅座椅姿态调节机构而言其舒适性能是本文的研究重点,即选择方案2来对比优化前后各性能指标的变化.将优化前、后的杆长通过Matlab进行仿真后进行对比:1)比较图4和图5发现优化前座椅姿态调节机构的驱动力矩随着交叉四杆机构在后倾过程中会出现突变的情况,表明座椅铰接处点处所受力发生突变,这严重影响座椅的使用寿命;而优化后座椅的驱动力矩在后倾过程中不仅没有发生突变现象,而且所需驱动力矩相较之前有明显的减小,符合预期效果;2)比较图6和图7会发现优化前与优化后相比,在刚开始后倾时,瞬时加速度由0.045 mm/s2下降到0.017 mm/s2左右,这样明显提高了使用者的舒适程度,同时也发现优化后加速度在座椅后倾过程中明显减小,提高了座椅动作时的安全性和舒适性,符合优化设计要求;3)比较图8和图9发现优化后座椅后倾时的工作空间相较优化前的工作空间有所提升,这极大满足了座椅不同使用者的要求.
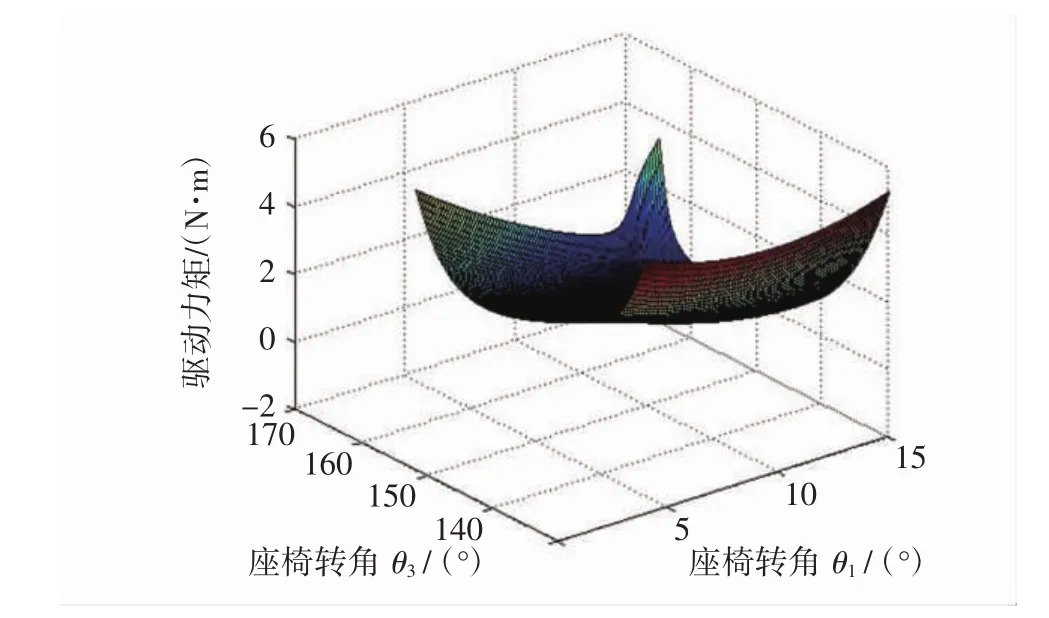
图4 优化前驱动力矩Fig.4 Driving moment before optimization
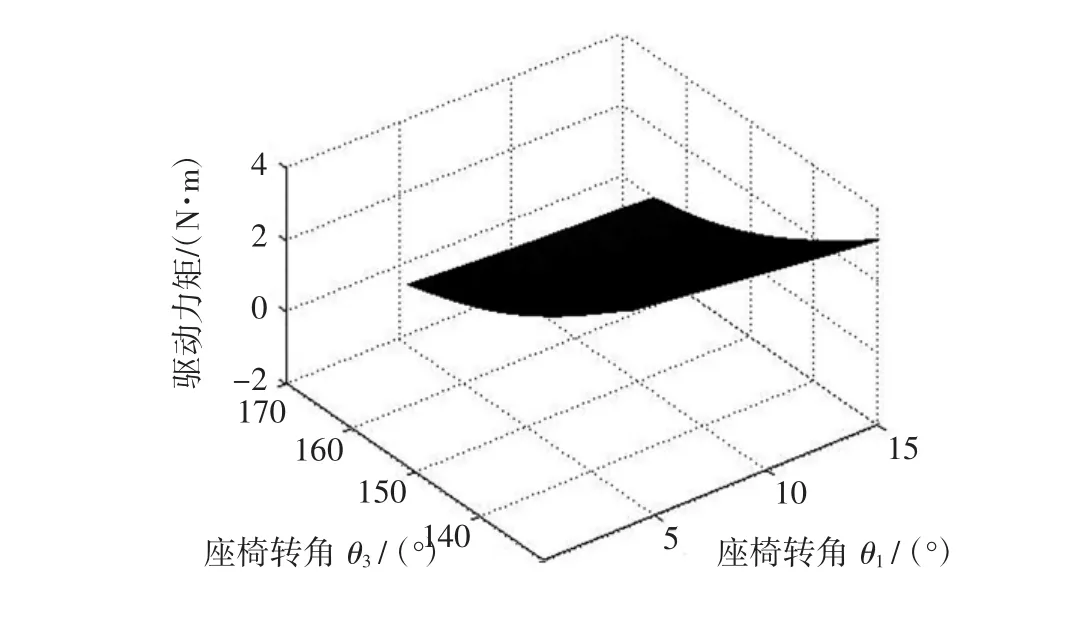
图5 优化后驱动力矩Fig.5 The optimized driving moment
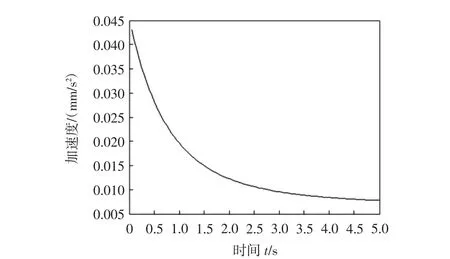
图6 优化前加速度Fig.6 Acceleration before optimization

图7 优化后加速度Fig.7 Acceleration after optimization
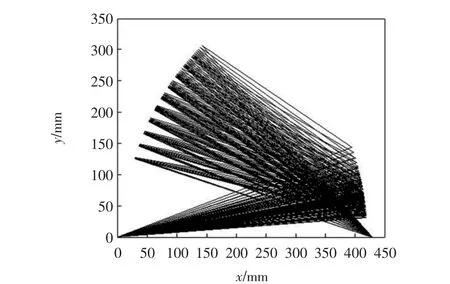
图8 优化前工作空间Fig.8 Before optimization work space
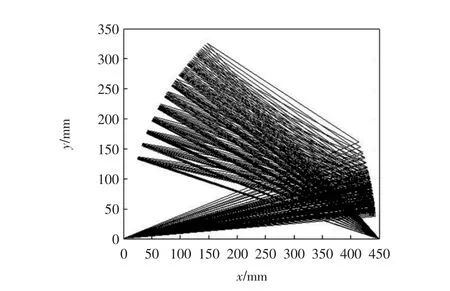
图9 优化后工作空间Fig.9 Optimized working space
5 结论
1)通过运动学分析和动态静力学分析分别建立了座椅姿态调节机构中座椅质心加速度即舒适性能指标、工作空间即工作性能指标以及驱动力矩即力矩性能指标与杆长参数之间的多目标优化数学模型,并采用NSGA-Ⅱ算法对座椅姿态调节机构参数进行了优化,获得了3个子目标Pareto最优解并从中选取了5组方案进行比较分析,这样能够更好的满足决策者的需求;
2)通过与原设计比较表明优化后座椅姿态调节机构性能有明显的提高,从而验证了本文所提出性能评价指标和优化方法的正确性,并达到了预期效果.
[1] 陆丰勤.多功能爬楼梯轮椅装置的研究及控制系统的设计[D].南京:南京理工大学,2008.
[2] 汤俊勇.轮腿混合式轮椅座椅姿态调节机构设计与运动学仿真[D].天津:河北工业大学,2015.
[3] 鲁文其,胡育文,梁骄雁,等.永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(3):75-81.
[4] 高媛.非支配排序遗传算法(NSGA)的研究与应用[D].杭州:浙江大学,2006.
[5] Deb K,Agrawal S,Pratap A,et al.A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization:NSGA-II[C]//Parallel Problem Solving from Nature.Berlin,Germany:Springer-Verlag,2000:849-858.
[6] 孔民秀,陈琳,杜志江,等.基于NSGA-II算法的平面并联机构动态性能多目标优化[J].机器人,2010,32(2):272-277.
[7] 孙文杰,李刚.基于综合操作性能指标的操作机多目标优化[J].机械工程学报,2014,50(17):52-60.
[8] 崔国华,周海栋,王南,等.基于Insight的3-UPS-S并联机器人机构多目标优化[J].农业机械学报,2013,44(9):262-266.
[9] 孔民秀,陈琳,杜志江,等.基于NSGA-II算法的平面并联机构动态性能多目标优化[J].机器人,2010,32(2):272-277.
[10]张亮,张继业,李田,等.超高速列车流线型头型多目标优化设计[J].机械工程学报,2017,53(2):106-114.
[11]杨文玉,孟富明.锻造操作机顺应性能评价与优化方法[J].机械工程学报,2010,46(23):121-127.
[12]孙立宁,楚中毅,曲东升,等.2-DOF平面并联机器人结构参数优化的研究[J].哈尔滨工业大学学报,2004,36(3):277-280.
[13]石志新,罗玉峰,陈红亮,等.机器人机构的全域性能指标研究[J].机器人,2005,27(5):420-422.
