基于半监督核均值漂移聚类的地震相识别研究
2018-01-30郝茜茜周亚同任婷婷
郝茜茜 ,周亚同 ,任婷婷
0 引言
地震相识别是地震层序划分的前提,是油气藏勘探和储层预测的基础[1].在地震剖面上包含着丰富的地质信息,已有很多聚类方法被用于地震相识别.例如K均值[2],模糊C均值聚类[3],DBSCAN聚类[4],但上述都是一些常规的聚类方法.
近年又涌现了一些性能优良的聚类方法.例如SOM聚类[5],次胜者惩罚竞争学习聚类[6]和均值漂移聚类.均值漂移[7]是一种基于非参数估计的密度聚类算法,通过迭代搜索特征空间中的样本点,使聚类中心始终向密度最大的方向移动.该算法迭代速度快,无需人为规定聚类个数且可以对任何的集群结构聚类,Subbarao等[8]和Vedaldi等[9]实现了均值漂移在核空间的聚类.此方法被广泛应用于目标跟踪[10]、图像分割[11-12]、图像去雾[13]和广播音频[14]等方面,但目前为止还未被用于地震相识别.
半监督学习是近年来较受关注的方法之一,通过将半监督学习与一些常规聚类方法结合,应用少量的先验信息去指导聚类过程以使聚类结果更准确.例如林超[15]通过对半监督学习方法与k均值聚类结合,解决了算法的约束违反问题.Kulis等[16]将半监督学习与图谱聚类结合优化了图形数据聚类.尹学松等[17]先根据成对约束得到投影空间后在投影空间进行k均值聚类,然后在由线性判别法得到的子空间中再次聚类.Tuzel等[18]和Anand等[19]实现了半监督学习与核聚类法的结合.
核均值漂移聚类不局限于集群结构的类型,适用于复杂多变的地震数据结构,半监督学习又可以根据已知的先验信息指导聚类过程.基于以上考量,本文研究基于半监督核均值漂移聚类(SKMS)的地震相自动识别算法.理论数据模型和实际地震数据聚类均表明SKMS是一种有效的地震相划分方法.
1 核均值漂移(KMS)聚类原理
在核均值漂移(KMS)聚类中,欧式空间扩展为一般的内核空间.令χ为输入空间,则有n个样本xi∈χ,i=1,…,n.假设空间 χ表示为 Rd,x 通过映射函数 φl,l=1,…,dφ映射到 dφ维特征空间 H,即

定义对角带宽矩阵为hiIdφ×dφ,i=1,…,n,y∈H,则在特征空间H中的核密度估计为
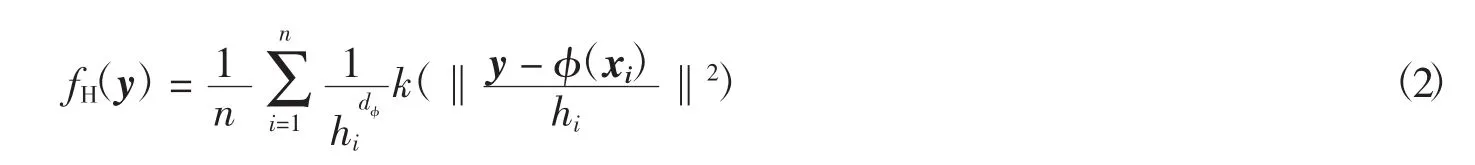
对公式(2)求梯度可得空间H中的均值漂移向量为

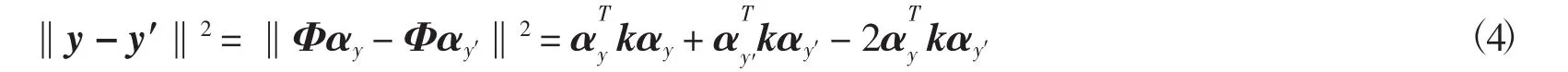
定义ei为特征空间H中的第i维标准基向量,有ei∈Rn,则φ(xi)=Φei,将此式与式(4)代入式(3)中有
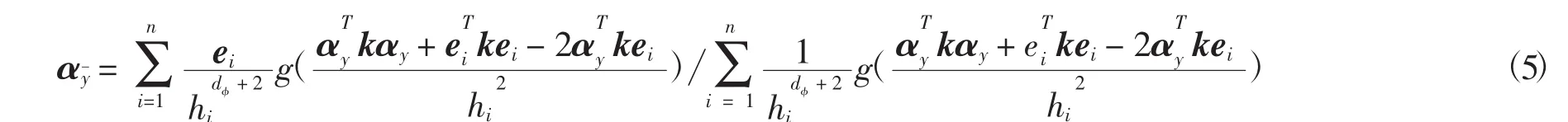
从而可以得到均值漂移向量,该方法同样收敛于局部分布模式.这样通过赋予合适的映射函数就可以实现核均值漂移聚类.
2 半监督均值漂移(SKMS)聚类原理
在核均值漂移算法的基础上,该算法采用成对约束来指导聚类过程.在聚类之前,需要根据先验经验采集must-link和cannot-link约束组成成对约束.聚类过程为:首先将所有点通过核函数映射到高维空间中,然后在高维核空间中对所有成对约束进行线性变换,最后将特征点全部投影到约束向量零空间,使两点之间距离符合距离目标参数的聚为一类.
2.1 通过更新核函数实现线性变换
对样本进行变换,就是将样本从特征空间向约束向量的零空间投影的过程,此过程可以通过更新式(5) 中的核矩阵隐形实现.定义(j1,j)2为成对约束,表示j1,j2被强制成为一对,既可以是must-link成对约束也可以是cannot-link成对约束,有.若给定nc个成对约束NC,dφ维的约束向量可以表示为其中n维向量zj表示为第j个成对约束的指标向量,则含nc个约束向量的约束矩阵A=ΦZ,其中Z= [z1,z2,…,znc]为n×nc阶指标矩阵.定义线性变换矩阵为

其中:s为a的缩放因子.当s=1/aTa时,该变换就变为从特征空间向约束向量a的零空间投影;当0〈s〈2/aTa时,该变换减小成对点之间的距离;当s〈0或s>2/aTa时,该变换增大成对点之间的距离.
令成对点的距离为d>0,则有


将约束向量a=Φz代入到公式(8)中得


2.2 通过logdet布雷格曼散度实现核函数更新
布雷格曼散度是一种类似距离度量的方式.若有n×n维的矩阵X和Y,则有布雷格曼散度公式如下

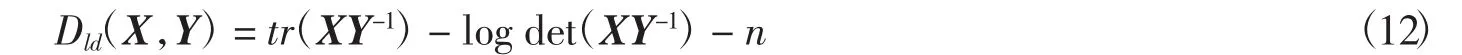
其中:X和Y为半正定矩阵且X和Y的秩不大于n.对X和Y进行奇异值分解,有X=V∧VT,Y=UΘUT,进而可以求得logdet布雷格曼散度

现通过logdet布雷格曼散度实现核函数更新.给定m个must-link成对约束集M和n个cannot-link成对约束集C,有m+c=nc.must-link约束的目标距离为dm,cannot-link约束的目标距离为dc,则最终的更新核矩阵问题转化为求logdet布雷格曼散度最小化问题,即目标函数为


由于在logdet布雷格曼散度中的第一个参数X要求必须是凸的,用logdet散度最小化更新核矩阵可以保证算法收敛到全局最优解.
3 应用SKMS进行地震相识别的步骤
用SKMS进行地震相识别的步骤如图1所示.对于给定地震数据,首先进行地震属性提取和归一化,然后对优选后的地震属性采用SKMS聚类法得到地震相识别结果.
在图1中需要用到SKMS聚类,它的具体步骤为:

图1 用SKMS进行地震相识别的步骤Fig.1 The steps of seismic facies identification using SKMS
步骤1:各参数初始化.初始化约束距离参数dm和dc,dm为must-link约束初始距离,dc为cannot-link约束初始距离;初始化成对约束集M和C;
步骤2:计算初始核矩阵k;
步骤3:采用logdet散度更新核矩阵kˆ;
步骤4:对于地震属性的n个样本点i=1,2,…,n
4 实验结果与分析
为了验证SKMS聚类效果,分别对理论模型和实际地震数据进行处理,将处理结果与k均值聚类、核k均值聚类(KK聚类)、谱聚类[20]、均值漂移聚类(MS聚类)、全局核k均值聚类(GKK聚类)[21]和自组织神经网络聚类(SOM聚类)等算法对比.
4.1 理论数据模型实验
在地质结构中通常含有褶皱、尖灭和套叠等结构单元.首先理论模拟出这3种结构,并采用SKMS聚类,然后将这3种理论结构模型采用上述5种算法对之聚类.聚类结果如图2~图4所示.
实验1:褶皱结构如图2所示.

图2 褶皱结构的各种算法聚类结果Fig.2 The clustering results of various algorithms for folds
实验2:尖灭结构如图3所示.
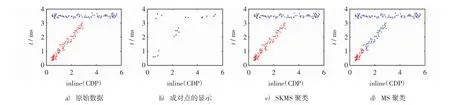
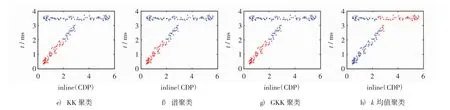
图3 尖灭结构各种算法聚类结果Fig.3 The clustering results of various algorithms for pinch-out
实验3:套叠结构如图4所示.

图4 套叠结构的各种算法聚类结果Fig.4 The clustering results of various algorithms for telescope

表1 理论数据模型的详细信息Tab.1 Detailed information on theoretical data models

表2 各算法运行时间对比Tab.2 Comparison of running time of each algorithm

表3 各聚类算法准确率对比(CA)Tab.3 Accuracy ratio of each algorithm (CA)
从表2看出,SKMS总体比KK、MS、K的运行时间长,但与GKK相比,总体运行时间短.在样本个数为202时,谱聚类的时间比SKMS长,随着样本个数的增长,SKMS比谱聚类的运行时间的增长速度快.对聚类结果的评价标准,本文采用准确性(cluster accuracy,简称CA)度量.从表3可以观察到:SKMS的聚类准确性明显优于其它的几种算法,SKMS在不同的理论模型上的准确性均达到了90%以上.而且SKMS在计算时均能正确估计聚类个数.
4.2 实际地震数据实验
本实验采用荷兰北海F3地震数据.在opendtect6.0和Matlab2013a软件平台下采用倾角控制中值滤波后的地震数据进行运算.选取联络测线1 000纵剖面,剖面范围为主测线的450-550道,时间线time的1724-1820部分,该纵剖面存在明显的波形反射构型.
从地震属性中选取相关系数较小的瞬时振幅、瞬时频率、瞬时相位属性,将这3种地震属性作归一化处理.应用这3种属性,采用SKMS对属性聚类,选取了3类共30个点如下所示,将这些点组成成对约束并采用SKMS聚类,效果如图5所示.

图5 SKMS聚类效果Fig.5 SKMS clustering result
在联络剖面1 000中,共标记了3类数据,如图5a)所示,因截取的剖面数据为25×101,即共有2 525个地震数据,所以标签数据占总地震数据数的1.19%,在SKMS聚类中,可以生成个mustlink成对约束,然后再构造同样个数的cannot-link成对约束,选取高斯核函数,其中σ为0.5,SKMS聚类将地震相划分为6类,如图5b)所示.
同样应用上述3种属性,分别采用不同的方法聚类,结果如下所示.
在KK聚类、谱聚类和GKK聚类中,均采用同一个高斯核函数,σ取0.5,聚类个数设为6类,如图6 a) ~图6 c) 所示.在MS聚类中,带宽值为2.5,聚类结果为6类,如图6 e) 所示.k均值聚类结果如图6 f)所示.SOM聚类为商业软件的聚类效果.SKMS与其他算法的聚类效果相比,层次更分明,层与层之间的边界清晰,在绿圈范围内,能够将一些微小地层区分出来.
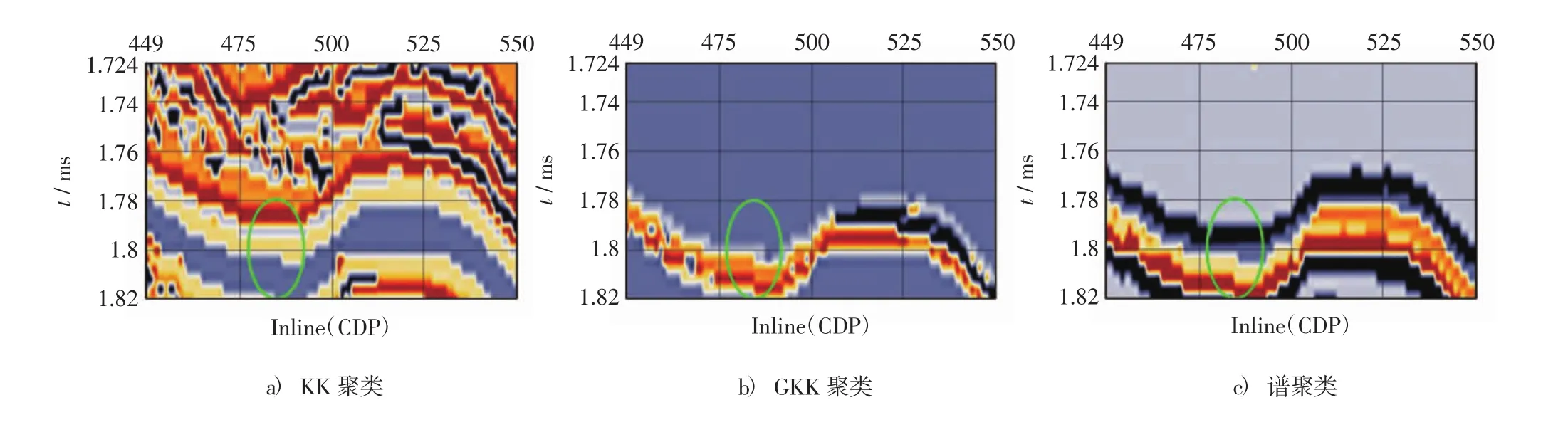
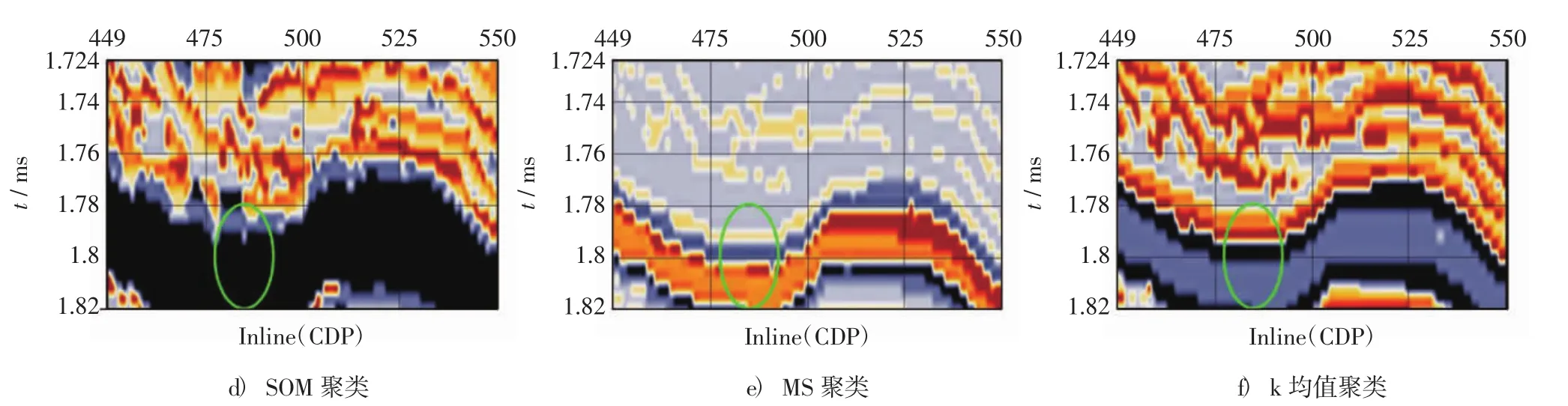
图6 各算法聚类效果Fig.6 clustering results of each algorithm
5 结论
本文采用SKMS对地震属性聚类,利用已知的少量先验信息对聚类过程约束,达到提高地震相划分结果的精确性的目的.均值漂移属于密度聚类,能够自动优化判断聚类个数,且可以对任意数据结构都有效.SKMS聚类法融合了MS聚类和半监督聚类的优势,将SKMS聚类与其他聚类算法相比,比无监督聚类的聚类结果准确度有了很大提高,划分地震相的层次更分明.
[1] Robert E.Sheriff.Structural interpretation of seismic data[M].American:American Association of Petroleum Geologists,1982:14.
[2] 庞锐,魏嘉.利用K均值聚类方法进行地震相识别[C]//臧绍先.中国地球物理学会第二十四届年会论文集.北京:中国地球物理学会.2008:132.
[3] 张阳,邱隆伟,李际,等.基于模糊C均值地震属性聚类的沉积相分析[J].中国石油大学学报自然科学版,2015,39(4):53-61.
[4] 杨瑞超.DBSCAN算法在地震相划分中的应用[D].西安:西安科技大学,2011:1-43.
[5] 张龚,郑晓东,李劲松,等.基于SOM和PSO的非监督地震相分析技术[J].地球物理学报,2015,58(9):3412-3423.
[6] Zhan Shifan,Lei Li,Wei Xiong,et al.Automatic geological body identification using the modified rival penalized competitive learning clustering algorithm[C]//Seg Technical Program Expanded.USA:Society of Exploration Geophysicists.2011:4424
[7] Cheng Yizong.Mean Shift,Mode seeking,and clustering[J].Pattern Analysis&Machine Intelligence IEEE Transactions on,1995,17(8):790-799.
[8] Subbarao R,Meer P.Nonlinear mean shift for clustering over analytic manifolds[C]//Jean-Philippe Tardif.IEEE Computer Society Conference on Computer Vision and Pattern Recognition.USA:IEEE Computer Society,2006:1168-1175.
[9] Vedaldi Andrea,Soatto Stefano.Quick shift and kernel methods for mode seeking[M].France:Computer Vision-ECCV 2008,2008:705-718.
[10]马丽,常发亮,乔谊正,等.基于改进的均值漂移算法的目标跟踪[J].计算机工程,2006,32(24):175-177.
[11]伍艳莲,赵力,姜海燕,等.基于改进均值漂移算法的绿色作物图像分割方法[J].农业工程学报,2014,30(24):161-167.
[12]白培瑞,李良,赵奇,等.基于均值漂移的医学超声图像分割改进算法[C]//中国智能自动化会议.南京:中国自动化学会,2009:1426-1431.
[13]陆海俊,汪荣贵,杨娟,等.基于均值漂移的暗原色先验图像去雾算法[J].合肥工业大学学报自然科学版,2016,39(9):1205-1210.
[14] 郑继明,俞佳.基于 Mean-Shift的广播音频聚类算法[J].计算机应用,2009,29(10):2741-2743,2750.
[15]林超.基于成对约束的半监督聚类算法研究及其并行化实现[D].西安:西南交通大学,2013:1-51.
[16]Kulis Brian,Basu Sugato,Dhillon Inderjit,et al.Semi-supervised graph clustering:a kernel approach[J].Machine Learning,2009,74(1):1-22.
[17]尹学松,胡恩良,陈松灿.基于成对约束的判别型半监督聚类分析[J].软件学报,2008,19(11):2791-2802.
[18]Tuzel O,Porikli F,Meer P.Kernel methods for weakly supervised mean shift clustering[C]//IEEE,International Conference on Computer Vision,ICCV 2009,Kyoto,Japan,September 27-October.DBLP,2009:48-55.
[19]Anand Saket,Mittal Sushil,Tuzel Oncel,et al.Semi-supervised kernel mean shift clustering[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2014,36(6):1201-15.
[20]Choromanska A,Jebara T,Kim H,et al.Fast spectral clustering via the Nyström method[M].Germany:Algorithmic Learning Theory.Springer Berlin Heidelberg,2014:367-381.
[21]Chen W Y,Song Y,Bai H,et al.Parallel spectral clustering in distributed systems[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2011,33(3):568-586.
