基于主成分分析和聚类分析的医保欺诈行为主动发现

尹菊芳+韩雪

摘 要 考虑到病人医保欺诈的多种可能性，本文采用主成分分析和聚类分析方法建立病人欺诈可疑度评价模型，对病人是否存在欺诈行为作出分析和判别。

关键词 主成分分析 聚类分析 医保欺诈 防范

中图分类号：TP311 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2017.12.069

Abstract Considering the many possibilities of patient's medical insurance and fraud， this paper uses principal component analysis and cluster analysis to establish the evaluation model of suspicious patients fraud， and analyzes and discriminates the patients' fraud.

Keywords principal component analysis； cluster analysis； medicare and fraud； prevent

0 引言

随着医改的不断深入，医疗保障体系不断拓展覆盖保障人群，做好医保欺诈的防范，尤其是在规范医疗行为方面显得尤为重要。在有关机构的调查中显示，过度医疗，分解住院，冒用出借医保卡，虚假收费等为目前欺诈比例最大的几个手段。本文将针对以深圳某医院一个月的35810个患者记录为例分析医保欺诈行为。根据病人单月内消费次数、消费金额、购药数量、购药种类及病人医保卡的使用人数等，采用主成分分析和聚类分析方法，找出可能存在欺诈行为的记录。

1 数据处理

1.1 指标变量的选取

目前社会上医保欺诈的手段多种多样，总体来说可归结为6种情况：拿着别人的医保卡配药，即一张医保卡被多个人使用；单次消费特别高，一个病人对应一个或多个账单，这些账单的费用有高有低，选取其中最高的费用作为一个考评指标；一张卡在一定时间内反复多次拿药；某段时间内消费总金额过高；某次购药数量很多；某段时间内反复购买大量药品。

因此我们选取6种评价指标进行主成分分析：对应的医保卡使用人数（）；单次最高消费金额（）；单月消费次数（）；消费总金额（）；购买药品总数量（）；单次最大购药数量（）。

1.2评价指标标准化

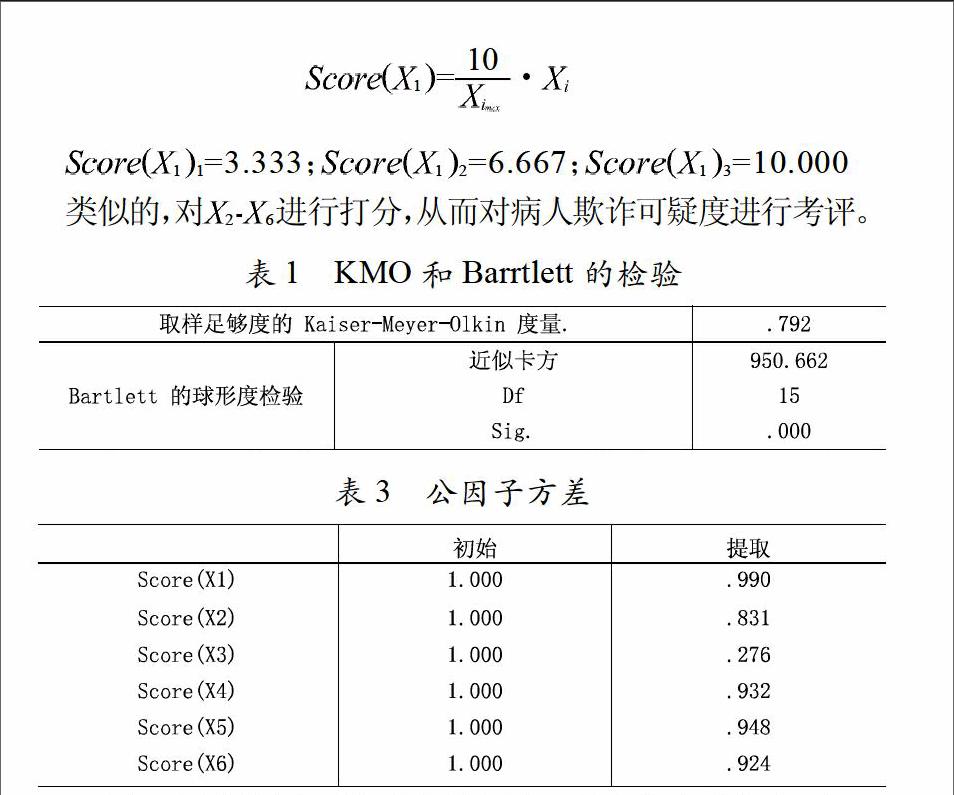
对每个病人的各个指标进行打分。设定每个变量的满分为10分，建立指标评分模型：

病人的指标变量具有不同的分数，分数越高代表欺诈的可能性越大，分数越低代表欺诈的可能性越小。例如，病人医保卡的使用人数是刻画病人是否正常使用医保卡的一个重要指标，即病人的医保卡使用人数越多，则病人欺诈的可能性越大。对于指标，病人医保卡的使用人数可能有三种情况，仅有一人使用，即 = 1；被两个人使用，即 = 2；被三个人使用，即 = 3。按照上面指标评分模型，可分别计算出相应的：

2 主成分分析

2.1 KMO和 Barrtlett的检验

使用SPSS软件对标准化的数据进行KMO和Barrtlett的检验：

由表1可以看出Barrtlett检验统计量为950.662，相应的Sig为0.000，相关系数矩阵与单位阵有显著差异，此假设被拒绝，同时，KMO值为0.792，原有变量适合作主成分分析。

2.2 相关系数矩阵

相关系数矩阵是6个变量两两之间相关系数大小的方阵，反映了变量之间的相关系数大小（见表2）。

2.3 公因子方差

公因子方差给出了主成分从原始变量中提取的信息（表3）。

可见，所有变量的共同方差均较高，各个变量的信息丢失都较少，因此本次主成分分析提取的总体效果较理想。

2.4 解释的总方差

各因子旋转前和旋转后的特征值、方差贡献率和累积方差贡献率的计算结果如表4：

其中第一列是因子编号，以后三列组成一组，每组中数据项的含义依次是特征值，方差贡献率和累计方差贡献率。由解释的总方差及特征值得碎石土图可以知道第一主成分的方差是2.476，第二主成分的方差是1.434，第三主成分的方差是1.000。根据累计贡献率超过80%的一般选取原则，主成分1、主成分2和主成分3的累计贡献率已达到了81.682%的水平，表明原来6个变量反映的信息可由三个主成分反映81.682%，能够反映主要信息， 主成分分析效果较理想。

2.5 成份得分系数矩阵

2.6 成份得分协方差矩阵

协方差是反映的变量之间的二阶统计特性，如果变量之间的相关性很小，则所得的协方差矩阵几乎是一个对角矩阵。这里得出的主成分的协方差矩阵是一个对角阵，则说明3个主成分相关性很小。

提取方法：主成份。构成得分。

3 K-means聚类分析

本文中使用SPSS19.0进行K-means聚类分析，将聚类的类别取为4，代表四种可能的欺诈程度。

3.1 初始聚类中心

SPSS软件会自动选择初始中心点，从表7得知SPSS自动选择的第一聚类的初始中心点为12.32，第二聚类的初始中心点为16.51，第三聚类的初始中心点为-0.78， 第三聚类的初始中心点为6.66。

当聚类中心内没有改动或改动较小而达到收敛。本文中当迭代次数达到50次时，达到设定的阈值，聚类中心不再更改。

3.2 最終聚类中心

表8是由综合得分聚类得来的最终聚类中心，可知第一聚类的中心为1.81，第二聚类的中心为5.32，第三聚类的中心为-0.46，第四聚类的中心为0.36.聚类中心的值，可描述病人欺诈的可能性大小，实际上，最终聚类中心的值越大，欺诈的可能性就越大.因此，可根据表8中的最终聚类中心的大小来确定最初定义的四类与聚类产生的四类之间的对应关系.

3.3 每个聚类中的案例数

可见，第一个聚类的最终中心点为1.81，案例数为3318，即可能存在欺诈的行为的记录为3318条，第二个聚类的最终中心点为5.32，案例数为260，即极可能存在欺诈行为的记录为260条，第三个聚类的最终中心点为-0.46，案例数为23050，即不存在欺诈行为的记录为23050条，第四个聚类的最终中心点为0.36，案例数为9182，即基本不存在欺诈行为的记录为9182条。

4结论

由统计得知，未使用医保卡人数所占的比例为38.23%，使用医保卡而不存在欺诈行为的所占的比例为39.73%，基本不存在欺诈行为的所占的比例为15.83%，可能存在欺诈行为的所占的比例为5.72%，极可能存在欺诈行为的所占的比例为0.49%，可能存在欺诈行为的和极可能存在欺诈行为的加起来共占6.21%，通过中华人民共和国人力资源和社会保障部官方网站的数据得知，中国的医疗欺诈比例约为6%，得出的结果与这个比例十分接近，由此可知的结果是基本可靠的。

参考文献

[1] 刘喜化，魏超.我国社会医疗保险欺诈研究综述.东方论坛，2013（6）.

[2] 何俊华.数据挖掘技术在医保领域中的研究与应用.计算机软件与理论，2011.4.20.

[3] 梁欣强.医保系统中数据挖掘的应用.电脑知识与技术，2014（19）.endprint