基于层次分析法探究高校年度优秀辅导员评比

程智龙+郝晓红

摘 要 高校年度优秀辅导员评比是提高学生工作能力以及加强辅导员自身建设的一种有效方法。本文运用层次分析法进行探究，通过对比较矩阵来确定各因素指标的相应权重，为科学化考核与评比获取相应指标体系，同时针对学生工作给予相应的建议。

关键词 层次分析法 优秀辅导员评比 高等教育

中图分类号：G451 文献标识码：A DOI：10.16400/j.cnki.kjdkx.2017.12.032

Abstract The evaluation of College annual outstanding counselors is an effective way to improve the ability of students' work and to strengthen the self construction of the counselors. In this paper， we use AHP to explore， through comparing the matrix to determine the corresponding weight of each factor index， and get corresponding index system for scientific assessment and evaluation， and give corresponding suggestions for student work.

Keywords analytic hierarchy process； evaluation of excellent counselors； higher education

2013年全國宣传思想工作会议上习近平总书记强调：“经济建设是党的中心工作，意识形态工作是党的一项极端重要的工作”。2016年12月7日-8日在北京召开全国高校思想政治工作会议上，再次强调：“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，思想政治工作从根本上说是做人的工作，必须围绕学生、关照学生、服务学生，要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面”。所以加强学生思想政治教育显得尤为重要。

1 高校优秀辅导员评比背景

高校辅导员工作是高校学生工作的重点，大学辅导员时高等学校师资队伍的重要组成部分和开展大学生思想政治教育的工作主体，其工作质量直接关系到高等教育的质量。加强辅导员工作，对促进辅导员队伍建设显得尤为重要。近年来各高校按照《中共中央、国务院关于进一步加强和改进大学生思想政治教育工作的意见》、教育部《普通高等学校辅导员队伍建设规定》部署，组织辅导员参加辅导员业务培训、学生专题工作案例理论学习、辅导员职业技能大赛等，提高高校学生工作的水平，加强辅导员职业技能，不断提高辅导员能力建设。

目前，高等学校对辅导员的工作评价[1]重点围绕：职业道德评价、工作能力评价、工作态度评价、工作业绩评价等四个方面开展。辅导员评价考核[2]归纳起来主要有以下几类：（1）定性评价与定量评价相结合的方式。所谓定性评价即为以参评人作为评价信息的对象，利用评价人即为评委或者部门领导结合评比规则和经验对工作的开展做出判断和评价，较为笼统；而定量评价通过采取一些统计数据为基础，按照参评准则求得评价结果，最后以数量形式予以表达出的形式得出最终结果。（2）采取全面考核方式，了解辅导员工作的整体情况。一般全面考核结合的是学工部（处）评分、院系评分、学生评价（评分）、辅导员自评等方式，是从不同层面人员收集和反馈信息，多视角多范围进行考核的一种评估行为，能够从各个层面和角度较多地了解辅导员的工作情况，也可以尽量减少人为因素的影响。

结合以上两类方法，没有明确评价辅导员评选指标体系以及科学的理论指导，表现出信息分割，主观因素较强等因素，无法对包罗万象的辅导员工作做到全面、客观、科学的评价，更难以比较辅导员在一年里表现的优秀程度。因此，如何全面、客观、科学地评价高等学校辅导员的工作以及如何建立一套以保证辅导工作质量为基础，促进辅导员自身发展，重视个体差异的科学评价体系来组织评选优秀辅导员显得尤为重要。

笔者经过自己亲身参与评比以及对部分高校采取方式进行比较分析，认为应该根据辅导员工作的性质和特点，将评价内容细化为可以操作和可测量的项目，为此需要对各类评判标准结合评价因素赋予不同的权重，尽可能对优秀辅导员的评比从各方面情况做出较为公正的评价[5]。为此借助数学建模工具，采用定量与定性相结合，设置相关模块，运用层次分析理论将主观判断用数量形式进行表达和处理，致力于高校优秀辅导员评比工作的科学化、规范化，并最终实现制度化。

2 利用AHP理论探究优秀辅导员评比

层次分析法[3]（Analytic Hierarchy Process，简称AHP）是由美国匹兹堡大学教授T.L.Saaty等人于20世纪70年代提出的一种系统分析与决策的综合评价方法。在作决策时，运用一般的数学方法为这类问题的决策提供了一种定性与定量相结合的方法。AHP在资源分配、选优排序、工程技术、和社会科学等众多领域中都得到了广泛的应用。

首先考虑建立一个优秀辅导员评比的内部独立的递阶层次结构。将年度优秀辅导员评比最终结果看作一个目标问题，影响该问题（评比）的因素按属性不同进行分层，同一层次元素作为准则，对下一层次的某些元素起支配作用，同时它与上一层次元素存在支配作用，这种从上至下的支配关系形成一个递阶层次。中间层为实现总目标而采取的措施、方案和政策或者所需考虑的准则、子准则。最低层为实现目标可供选择的各种措施、决策方案等，用于解决问题的各种途径和方法，也称为方案层。endprint

结合辅导员工作与职责、性质与评价要求，建立优秀辅导员的最终评定主要集中在以下四个方面：①思想教育：思想政治工作与学生能力培养；②学生评价：围绕学生开展日常管理以及服务学生成长成才；③部门初评：学院评价，学生处初评；④个人述职：从工作思路、特色、创新、取得成效进行述职，展示自己。

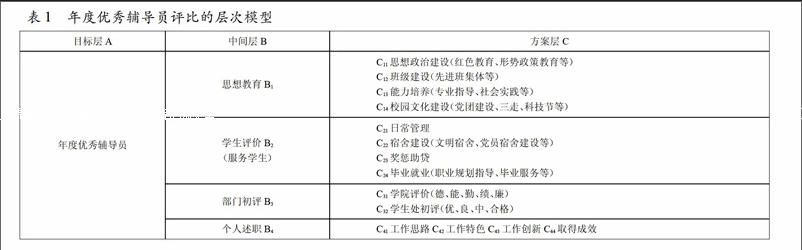
因此我们将目标层定位为：年度优秀辅导员，中间层则为：思想教育、学生评价、部门初评、个人述职等四方面，四方面之间是完全独立的，也就是相互不影响，而这四方面因素之间又分别由2～4子类组成，我们把它们看作是方案层，层次结构模型如表1所示。

运用层次分析理论比较上述中间层四个方面 B={B1，B2，B3，B4}对目标的影响，确定它们在A中所占的比重。每次取两个因素和，以表示和对A的影响的大小之比，全部比较结果用矩阵A=（） n€譶表示。为此笔者通过发放调查问卷形式，以表2，1～9及其倒数作为标度问卷调查50位在职辅导员，通过有效问卷的数据取平均值得到判断矩阵A，见表3。

上述权重为运用MATLAB软件运算得出，根据上述分析，年度优秀辅导员评比注重思想教育，这体现思想教育为高校辅导员工作重心，这也符合高校思政工作特点。为了能够更好地量化优秀辅导员的评比，为此我们需要对上述四个方面进行科学的赋值，每一项均为赋值100分。例如思想教育环节可以通过自评以及总结性材料进行量化打分；学生评价方面直接采用网络调查问卷评价辅导员；部门初评结合两部门之间考核，量化为百分制；个人述职方面，由参评辅导员上台演讲展示，进行评比打分。最后结合权重得出参评人员的最终得分。

假设辅导员甲四项得分分别为：85、92、90、88，通过乘以权重系数最终得分为87.7，辅导员乙四项得分分别为：92、94、91、85，通过乘以权重系数最终得分为90.5，依此类推，对参评人员进行最终打分，确定优秀人选。

3 优秀辅导员评比在学生工作中的启示

明确立德树人，加强思政引导。高校人才培养以立德树人为根本任务，辅导员属于高校思想政治工作的先锋，在培养中国特色社会主义事业合格建设者和可靠接班人中发挥着重要作用。辅导员要坚持用中国特色社会主义理论体系武装头脑，用社会主义核心价值观凝聚人心，不断增强青年学生的道路自信、理论自信、制度自信。

注重围绕学生，增强服务意识。辅导员是服务学生成长成才的一支重要力量，在学生成长中、发挥服务育人职能有着重要的作用。在围绕学生的基础上，把日常管理、文明宿舍建设、心理教育就业服务融入学生学习、生活、实践等方方面面，及时解决学生疑惑；邀请企事业单位、创业典型等走进学院举办报告会、模拟招聘会等，以考研、求职、创业等不同层面分类别进行指导，在工作中增强服务意识。

增强自身建设，提高工作能力。辅导员具有教师以及管理人双重角色，承担着行政事务和教育教学的任务。[4]“要给学生一滴水，首先自己应有一桶水”，辅导员是学生成长的指导者和引路人，辅导员指导学生，也是自身能力素质不断完善和提升的过程。在处理学生事务中形成自己的工作特色，同时经过自身的摸索利用互联网网络的学习、参加的培训以及辅导员职业技能大赛等运用于工作中不断创新。因此，辅导员在工作中，要勤于总结，善于观察、勇于创新，虚心向专家、同行学习。加强理论创新，提升科研能力，在总结中成熟使自身的能力得到全面的发展，提升工作能力。

基金项目：教学研究项目“基于应用型人才培养的研究——《高等数学》教学改革探索”（2016xjjyxm04）

参考文献

[1] 冯刚，杨曉慧.高等学校辅导员工作概论[M].高等教育出版社，2011.10.

[2] 袁立辉.对辅导员评价与考核的几点思考[J].教育论丛，2011.3：81.

[3] 郭大伟.数学建模[M].安徽教育出版社，2011.

[4] 吕冬诗，程慧.基于差距模型评价辅导员服务质量的研究[J].思想教育研究，2012.3（206）：92-95.

[5] 王志华等.高校辅导员评价标准研究[J].教育研究，2012.9（392）：86-90.endprint