基于SA算法的灰色Verhulst模型在软土路基沉降预测中的应用
2018-01-27邱红胜赵勇强付绍卿胡玉华
邱红胜,赵勇强,付绍卿,胡玉华
(1.武汉理工大学 交通学院,湖北 武汉 430063;2.中交第二公路勘察设计研究院有限公司,湖北 武汉 430056)
0 引 言
近年来我国公路建设飞速发展,而在一些多软土地区,公路路基在施工完成后会产生较大的工后沉降,造成经济损失和人员伤亡。因此,对软土路基的沉降分析非常重要,其对于确保公路工程质量和降低施工成本都有着极大的研究意义和实用价值。
目前,国内外对于软土路基的沉降预测已经有了较深入的研究,常用的预测方法有理论计算法[1],灰色预测法[2],指数曲线法[3],神经网络法[4]等。其中灰色预测法源于1982年我国著名学者邓聚龙院士提出的灰色系统理论[5],该理论将部分数据已知,部分未知的小样本信息称为灰色信息,通过对灰色信息的生成和开发,提取有价值的数据,从而实现对系统运行行为,变化规律的正确描述和有效监控。软土路基的沉降监测所需时间周期较长,往往难以得到足够的沉降数据,因此监测得到的信息是不完全的,属于灰色信息,可适用于灰色预测。
灰色Verhulst模型是灰色预测模型中的一种,主要用于描述灰色信息先增长,后逐渐趋向稳定的变化过程,即s型曲线过程,这与软土路基的沉降趋势是一致的,笔者在传统灰色Verhulst模型的基础上,利用SA算法(又称模拟退火算法)对模型进行了优化,提高了沉降预测精度,解决了传统模型预测误差较大的问题,为工程中的路基沉降问题提供了一种新的研究方法。
1 传统灰色Verhulst模型建模机理
设s(1)为工程实测得到的沉降序列,s(0)为s(1)的一次累减序列,有
s(1)=[s(1)(1),s(1)(2),…,s(1)(n)]T
(1)
s(0)=[s(0)(1),s(0)(2),…,s(0)(n)]T
(2)
其中:
s(0)(1)=s(1)(1)
(3)
s(0)(k)=s(1)(k)-s(1)(k-1),k=2,3,…,n
(4)
设t(1)为非等间隔的时间序列,t(0)为t(1)的一次累减序列,t(0)和t(1)均为非负序列:
t(1)=[t(1)(1),t(1)(2),…,t(1)(n)]T
(5)
t(0)=[t(0)(1),t(0)(2),…,t(0)(n)]T
(6)
其中:
t(0)(1)=t(1)(1)
(7)
t(0)(k)=t(1)(k)-t(1)(k-1),k=2,3,…,n
(8)
设z(1)为灰色Verhulst的背景值,z(1)由s(1)邻均值等权生成,其中:
z(1)=[(z(1)(1),z(1)(2),…,z(1)(n)]T
(9)
z(1)(k)=0.5s(1)(k)+0.5s(1)(k-1),k=2,3,…,n
(10)
则得灰色Verhulst模型:
s(0)(k)+az(1)(k)=b[z(1)(k)]2
(11)
式中:a为发展系数,b为控制系数。
灰色Verhulst模型白化方程为
(12)
令:
(13)
可推导出
s(0)(k)=-az(1)(k)t(0)(k)+b[z(1)(k)]2t(0)(k)
(14)
设:
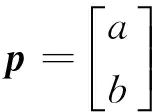
(15)
将方程改写为矩阵形式,则有:
(16)
s(0)=BP
(17)
上述方程组中s(0)和B为已知量,P为待定参数序列,由于变量a,b只有两个,而方程个数有n-1个,而且n-1>2,方程组无解,只能得到相对解,但可以通过最小二乘法得到最小二乘解。故可求得方程最小二乘解为
(18)
将求得的a,b值代入灰色Verhulst模型白化方程,可求得白化方程的解为
(19)
由方程解可以得出灰色Verhulst模型的时间响应序列表达式为
k=1,2,…,n
(20)
式(20)即沉降预测表达式,对其取极限可得到软土路基的最终沉降量:
(21)
2 模型优化与改进
2.1 优化原理
在灰色Verhulst模型的建立过程中,背景值z(1)对于模型参数的计算有着较大的影响。从几何上看,背景值实质上是通过梯形积分公式近似计算出的s(1)(t)与t轴在区间[k-1,k] 上所围成的面积值,由于梯形积分公式的代数精度较低,通过背景值求得的模型参数并不是最优解,导致传统灰色Verhulst模型在进行路基沉降预测时很可能会出现较大的误差,使得沉降预测不能满足精度的要求,故还需要对模型进行改进和优化,以提高预测的准确性。
对式(20)进行变形得到:
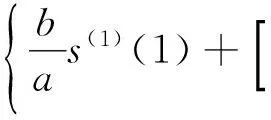
(22)
令:
(23)
将p和q代入式(22)可得到等式:
(24)
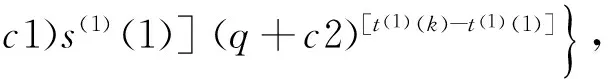
(25)
只需求出修正系数c1和c2,便可得到p和q的最优解,为此,构造平均相对误差函数f(c1,c2),该函数可看成含有两个自变量c1和c2的二元函数,通过以平均相对误差最小为目标来确定c1和c2的值,从而对p和q进行修正。其中:
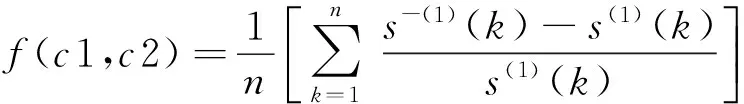
(26)
由于平均相对误差函数f(c1,c2) 是一个非常复杂的函数,函数中包含大量嵌套矩阵的运算,因此无法求出函数的绝对最优解,但可以通过SA搜索算法的寻优能力,求出c1和c2的相对最优解。
2.2 求解算法
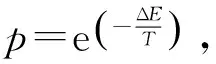
SA算法计算过程简单明了,可以有效避免在优化过程中陷入局部极小,适用于复杂的非线性求解问题,故选用SA算法来求解平均相对误差函数f(c1,c2)中c1和c2的相对最优解。求解具体流程如下:
1) 建立灰色Verhulst模型,得到时间响应序列表达式s-(1)(k);
2) 构造以修正系数c1和c2为自变量的平均相对误差函数f(c1,c2),将其作为目标函数;
建立了基于MDS跟踪传感器位置的状态方程和测量误差.设系统状态定义为N2×1,xk=vect(Bk)的向量,相应的状态方程可以表示为
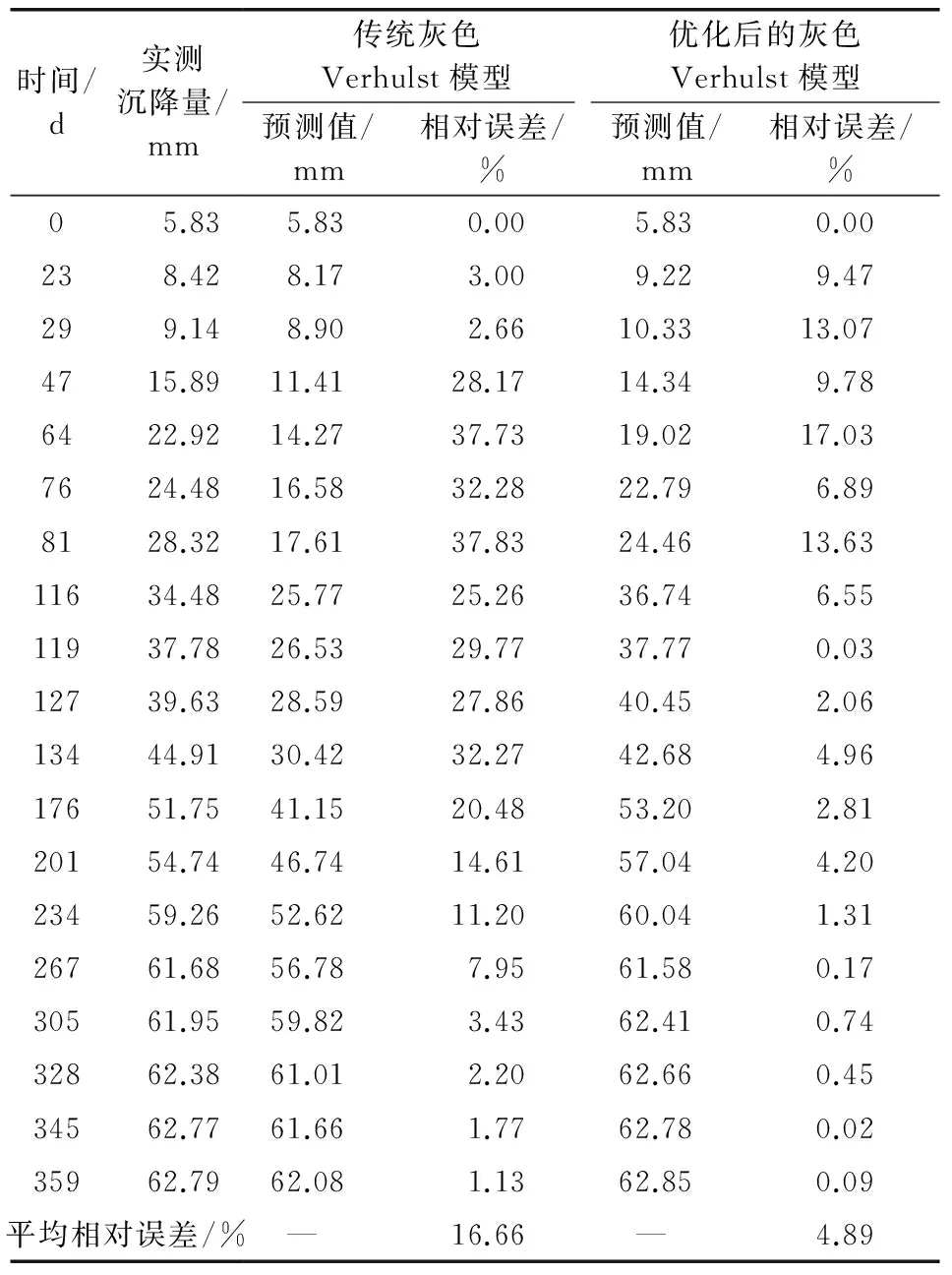
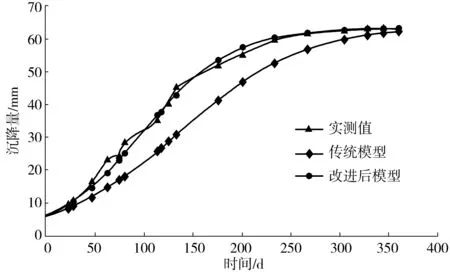
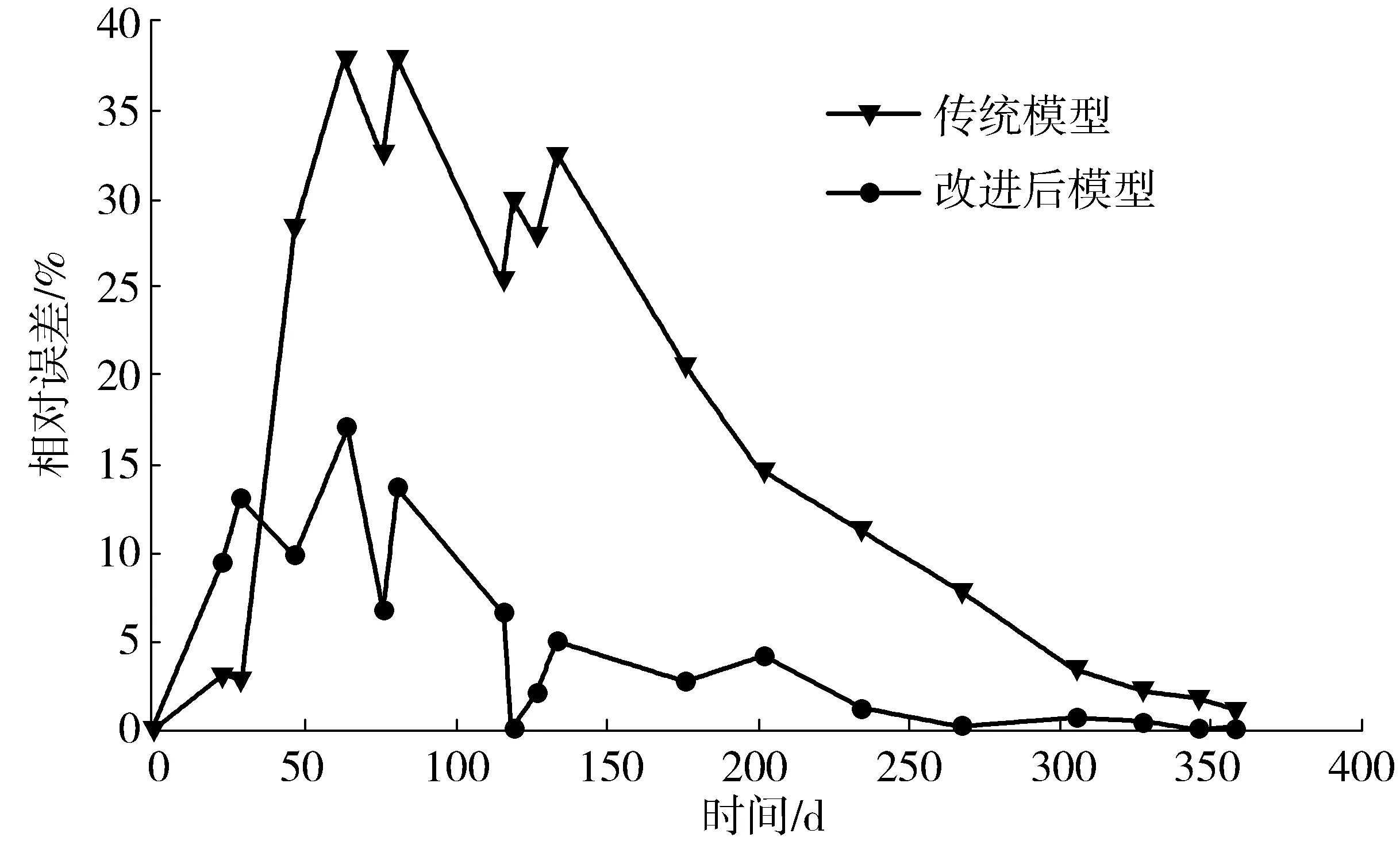
3) 确定初始温度为控制参数T,终止温度T终止为终止条件,确定冷却系数r,有0 4) 产生一组初始解w=(c10,c20),将初始解w代入目标函数得f=(c10,c20); 8) 对初始温度T进行冷却,即T=rT,使T逐渐减小; 9) 当T减小到一定值时,若满足终止条件T≤T终止,运算结束,此时解为最优解;若仍有T≥T终止,则重复循环5)至8)步骤,直到T满足终止条件为止,最后输出最优解。 该工程实例为内蒙古沙漠地区乌审召生态工业园区嘎鲁图段一级公路的软土路基,路段长度约为1 km。该段路基地处沙漠沼泽地区,属于地下水和地表水排水不畅的低地势段,所在地基表层细沙厚度为0.2 m,细沙以下为厚度3.5~5.4 m的粉土及淤泥质粉土夹层,地下水位在基底以下0.6 m。路基设计的填土高度为3.6 m,路基在堆载工况下沉降固结。选取典型路基观测断点K35+270,通过在该点断面埋设沉降板进行监测,得到该点断面的道中沉降数据见表1。 表1 K35+270道中断面沉降值Table 1 The settlement value of middle section of K35+270 road 笔者利用Python编程语言来实现模型的建立和优化,Python[8]是一门开源编程语言,其语法简洁优美,功能强大,有着丰富的库工具支持,非常适合用于算法实现和科学计算。根据表1中的数据,通过Python语言编写程序建立灰色Verhulst模型,使用SA算法对模型进行优化求解,其中算法参数设置如下:控制参数T=10 000,初始解w=(0,0),冷却系数r=0.985,新解的产生机制如下: (27) (28) 输入参数,经循环计算后,共得出763组解,将得到的所有解绘成散点图,如图1。 图1 解值散点图Fig. 1 The scatter plot of solutions 从图1可以看出,f值较小的点分布较为集中,白色点区域为所有f<0.005对应的点的集合,即平均相对误差小于0.5%对应点集。从该区域中选取最小f值所对应的点,即为修正系数c1和c2的相对最优解。 最终求得模型参数a=-0.016 450,b=0.000 258,修正系数c1=0.000 18,c2=0.006 00。将求得解代入式(23)得到表达式: (29) 对s-(1)(k)取极限: (30) 得到路基在监测点的最终沉降量为63.76 mm。为了验证优化后模型的准确度,分别计算出传统模型和优化后模型在不同时间的预测值,以及对应的相对误差,结果见表2。 表2 预测结果对比Table 2 Comparison of prediction results 由表2可见,优化后的灰色Verhulst模型的相对误差普遍要小于未优化的传统模型的相对误差。对相对误差取平均,得到传统模型的平均相对误差为16.66%,而优化后的灰色Verhulst模型的平均相对误差为4.89%,远小于未优化的模型的平均相对误差,因此优化后的模型有着更高的准确度。为了更进一步对比分析,将表2中的预测值绘成模型在优化前后的沉降预测曲线,将实测数据绘成实测值曲线,结果见图2。并将表2中两种模型的相对误差值也绘成曲线进行对比,结果见图3。 图2 沉降曲线对比Fig. 2 Comparison of settlement curves 图3 相对误差曲线对比Fig. 3 Comparison of relative error curves 图2将实测值曲线和优化前后的灰色Verhulst曲线进行对比,可以看出,传统灰色Verhulst曲线与实测值线相差较大,而优化后的灰色Verhulst曲线与实测值线更加接近,变化趋势也更加一致。而从图3可更直接地看出优化后的灰色Verhulst模型相对误差更小,且随着时间推移,模型的相对误差有着逐渐收敛的趋势,最终将趋近于0。这说明优化后的灰色Verhulst模型有更高的精确度和可行性,更适用于对路基沉降的预测。 传统灰色Verhulst模型采用梯形积分公式计算背景值,导致其预测精度低,误差大。笔者针对以上缺陷,将模型的时间响应序列表达式进行变形,加入修正系数,鉴于模型计算的复杂性,引入SA搜索算法来求解模型参数的相对最优解,从而实现了对模型的优化和改进。 将优化后的模型应用于实际的路基沉降预测,计算得到该段公路路基在监测点的最终沉降量为63.76 mm。通过对比分析模型在优化前后的沉降预测曲线,以及相对误差变化曲线,得出优化后的灰色Verhulst模型的预测精度显著提高,且相对误差随时间变化呈收敛趋势,表明经SA算法优化后的灰色Verhulst模型有着更高的精确度和可靠性,可以更好地应用于工程实践。 [1] 李成柱,周志芳.地面沉降的数值计算模型与流固耦合理论综述[J].勘察科学技术,2006(6):14-20. LI Chengzhu,ZHOU Zhifang.Review of numerical calculation models for land subsidence and fluid-solid coupling theory[J].SiteInvestigationScienceandTechnology,2006(6):14-20. [2] 朱杰,孙树林.灰色模型在软土路基沉降预测中的应用[J].路基工程,2006(4):84-87. ZHU Jie,SUN Shulin.Application of gray mode for predicated subgrade settlement on soft soil ground[J].SubgradeEngineering,2006(4):84-87. [3] 高燕希,莫志兵,魏金胜.指数曲线法在软土地基沉降预测中的优化与应用[J].交通科学与工程,2011,27(2):1-5. GAO Yanxi,MO Zhibing,WEI Jinsheng.Optimization and application of exponential curve method in soft soil foundation settlement prediction[J].JournalofTransportScienceandEngineering,2011,27(2):1-5. [4] 王志亮,许可.高速公路沉降预测神经网络法应用研究[J].低温建筑技术,2004 (1):36-38. WANG Zhiliang,XU Ke.Study on application of neural network method in settlement predication of highway[J].LowTemperatureArchitectureTechnology, 2004 (1):36-38. [5] 肖新平,毛树华.灰预测与决策方法[M].北京:科学出版社,2013. XIAO Xinping,MAO Shuhua.GreyForecastingandDecisionMakingMethod[M].Beijing:Science Press,2013. [6] 谢云.模拟退火算法综述[J].微计算机信息,1998(5):63-65. XIE Yun.A summary on the simulated annealing algorithm[J].MicrocomputerInformation,1998(5):63-65. [7] METROPOLIS N, ROSENBLUTH A W, ROSENBLUTH M N, et al. Equations of state calculations by fast computing machines[J].JournalofChemicalPhysics,1953,21(6):1 087-1 091. [8] 沈殊璇,薄亚明.适合于科学计算的脚本语言Python[J].微计算机应用,2002,23(5):289-291. SHEN Shuxuan,BO Yaming.Python-a script language fit for science computation[J].MicrocomputerApplications,2002,23(5):289-291.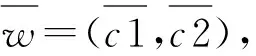
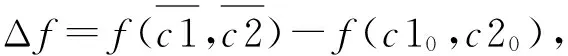
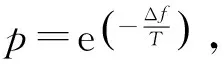
3 工程实例应用与分析
3.1 工程概况
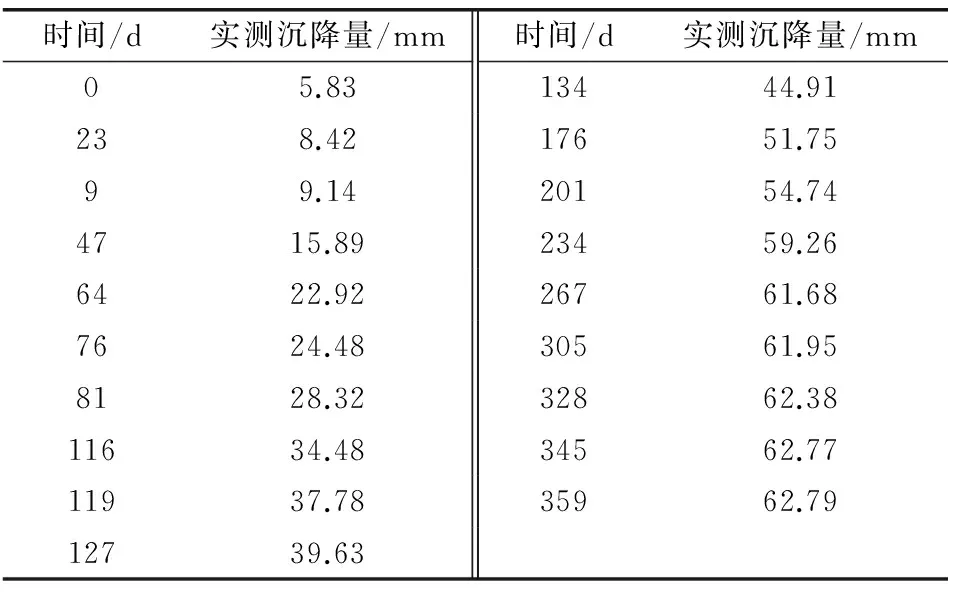
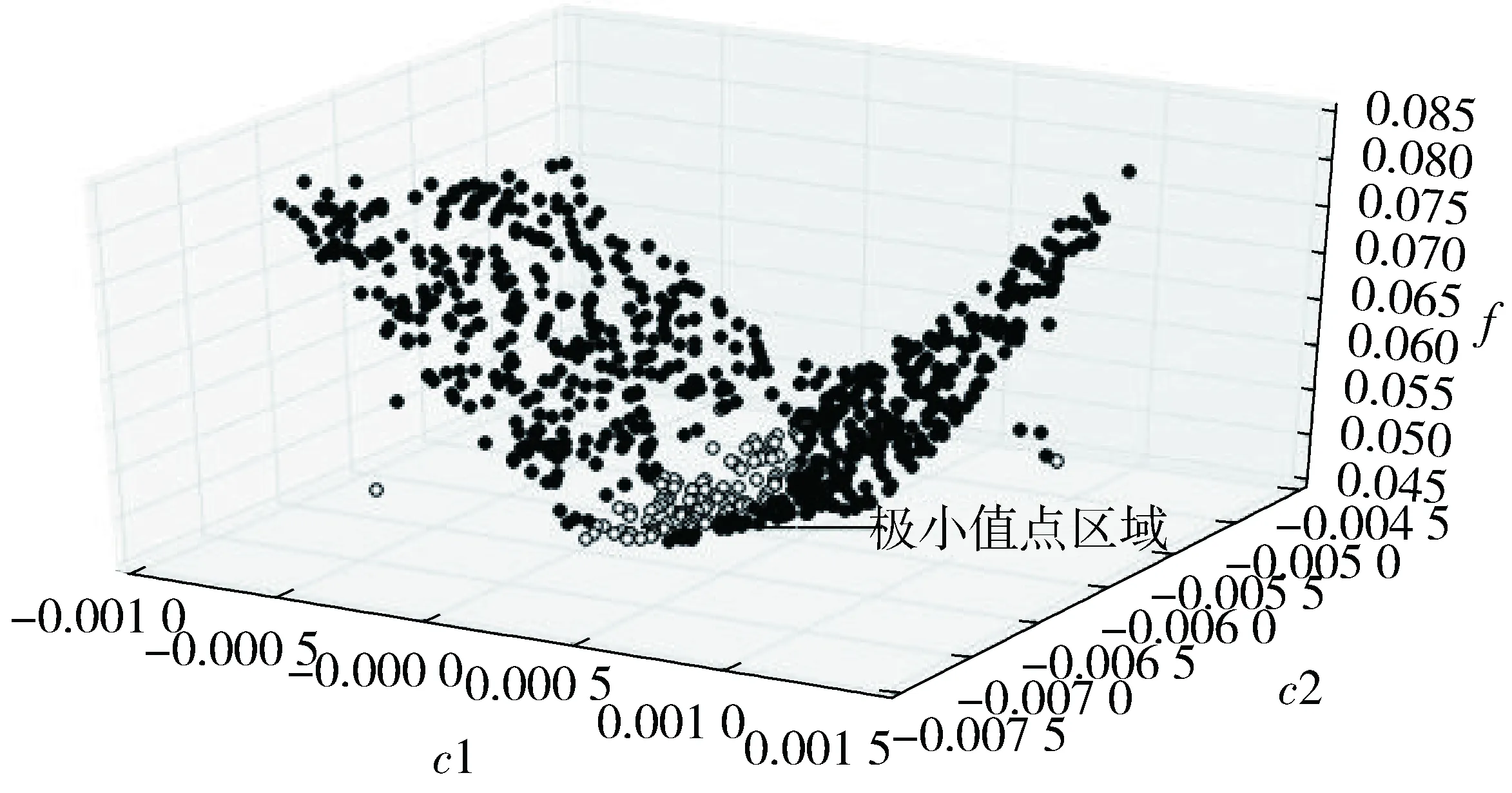
3.2 沉降预测和误差分析

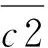
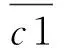
4 结 语
