基于BP神经网络的沥青混合料疲劳性能预测模型

谢春磊，张 勇，耿红斌，王学营1，

(1.内蒙古自治区交通建设工程质量监督局，内蒙古 呼和浩特 010070；2.内蒙古高等级公路建设开发有限责任公司，内蒙古 呼和浩特 010070；3.内蒙古自治区道路结构与材料重点实验室， 内蒙古 呼和浩特 010070)

0 引 言

沥青混合料的疲劳寿命预估是一个经久不衰的话题。早在20世纪60年代，美国的C.L.MONISMITH等[1]就建立起了基于应变控制的经典疲劳寿命预估模型。随后的美国SHRP计划及相关后续研究中，以加州大学Berkely分校为代表的研究者们又对疲劳性能进行了大量研究，并提出了各种各样的疲劳性能预估模型[2]，但这些研究主要将注意力放在路面结构设计层面上，并未关注混合料本身[3]。随着研究的深入，更多针对混合料自身影响因素的疲劳模型被提出。这其中以C.L.MONISMITH等[4]创立的模型应用最广，他们在大量试验数据的基础上，建立起了基于沥青用量、空隙率与应变水平的疲劳寿命回归方程。这之后，大量基于J. T. HARVEY模型的改良或变体模型也被提出。

目前疲劳寿命预估模型种类数量众多，且近些年来还出现了包括耗散能[5]在内的新型疲劳寿命分析方法，但由于疲劳损害影响因素众多，且具体作用机理仍未完全明确，目前的疲劳寿命预测模型难以做到精确的预测与防治[6-8]。鉴于此，笔者尝试从新的角度来对疲劳寿命进行预测。

神经网络是一种起源于生物学的运算模型。它可以通过模仿动物神经网络行为特征，对信息进行学习以及处理[9]。目前，已经有诸多将神经网络算法应用于道路工程的研究。谭忆秋等[10]指出，基于MATLAB平台的BP神经网络模型对沥青低温弯拉应变预测结果与实测结果误差在工程要求精度范围以内。王震宇[11]的研究表明，神经网络模型可以对沥青老化情况进行较高精度的预测。在具体针对沥青混合料疲劳寿命预测的领域，近年来也有不少成果。F.P.XIAO[12]曾提出一种预估疲劳寿命的数学模型，采用了回归分析和神经网络方法对再生橡胶沥青混合料的疲劳寿命进行预测。吴宏宇等[13]采用UTM试验机所得到的数据对一种基于混沌理论的神经网络进行训练，发现网络可以在一定程度上指导试验参数的选取，提高试验效率。而袁斌等[14]应用神经网络，针对荷载间歇时间、加载频率、试验温度、沥青混合料空隙率、沥青软化点、沥青用量等多个疲劳寿命关键影响因素进行了研究，得出了一种理论较为完备，具有实用性的预测模型。由于疲劳破坏影响因素众多，使用传统疲劳方程进行拟合时较为繁琐。而神经网络模型中自变量个数不受限制，通过调整内部结构可以充分逼近任意复杂的非线性关系，因此在构建疲劳寿命预测模型时具有普通方程所不具有的优势。但当前的研究主要都致力于预测模型的搭建，针对传统模型与神经网络模型预测效率比较的研究较少。

笔者拟采用四点弯曲疲劳试验仪进行宏观疲劳试验，将所获得的数据对神经网络进行训练，搭建起基于神经网络的沥青混合料疲劳寿命预测模型，并对比传统疲劳方程模型与神经网络预测模型的预测效果，从而验证神经网络模型应用于疲劳寿命预测的可行性。

1 网络结构

BP神经网络是神经网络中一种常用的类型，其理论清晰，性能优秀，且相较于其他网络也更易于搭建(利用MATLAB即可完成)，因此适合于非算法研究的工程设计人员使用。BP神经网络的结构多由1个输入层、1个隐藏层和1个输出层组成，各层由若干个节点构成，每一个节点的输出值与输入值的关系由权值和阈值决定。输入层包含m个节点(对应m个输入项)，其输入向量为X=(x1，x2，…，xj，…，xm)T，隐含层包含k个节点，其输出向量为Y=(y1，y2，…，yj，…，yk)T，输出层则只有一个节点，其计算输出为O=(o1，o2，…，oi，…，on)，而数据期望的输出为D=(d1，d2，…，di，…，dn)(n为训练样本组数)。输入层到隐含层之间的连接权用矩阵V表示，V=(vij)m×k。其中元素vij表示输入层第i个节点与隐含层第j个节点间的连接权。

在训练网络时，首先对连接权矩阵随机赋一较小的初值，然后将样本的各指标数据作为输入项带入网络进行计算，得到神经网络输出与实际数据之间的差值，称为网络误差Ei，当网络的总误差E大于训练目标时，神经网络就会发出误差信号δ对层之间的连接权值进行调整，并采用调整之后的连接矩阵再次计算网络误差，直到符合要求。

沥青混合料的疲劳破坏是个极其复杂的过程，其疲劳寿命受到设计指标，施工质量，荷载水平等众多因素的影响。如果从混合料自身的受力特性出发，有研究表明[4]，其疲劳寿命主要受到沥青含量、空隙率、应变水平等因素的影响。笔者拟建立起以沥青含量、空隙率、应变水平为输入项，疲劳寿命为输出项的预测模型。即结构为3-20-1的单隐层神经网络模型。其中3代表沥青含量、空隙率和应变水平3个输入项，20代表隐藏层的节点个数，1代表1个输出项，即疲劳寿命。隐藏层传输函数选择双曲正切S形函数，输出层传输函数选择线性函数。

BP神经网络的隐藏层节点个数对预测精度有显著影响。节点个数太少，网络无法完全呈现出样本的关联特性；节点个数太多，网络容易过拟合。一般根据经验和试验来确定节点数量。经过多次调试，最终选择20个节点，学习速度取0.01，训练最大终止次数为1 000 000，采用附加动量方法“traingdm”函数进行学习。

神经网络模型结构确定后，需要对其进行训练才能进行仿真预测。笔者所需的训练样本通过室内四点弯曲疲劳试验获得。

2 疲劳试验

2.1 混合料设计

试验使用埃索70号基质沥青。所用石料的粒径组成为13.2～9.5 mm、9.5～4.75 mm、4.75～2.36 mm、2.36～0.075 mm 4档。2.36 mm以上粗集料使用江苏溧阳产玄武岩，2.36 mm(含)以下集料使用浙江安吉产石灰岩。沥青与集料各项指标均满足规范要求。

根据马歇尔试验取4.4%为最佳沥青用量。为保证神经网络训练所采用的数据覆盖面足够广，且达到理想的覆盖密度，疲劳试验混合料试件成型选取4%、5.5%、7%三种沥青含量。

2.2 试验结果

采用由澳大利亚IPC公司生产的四点弯曲疲劳试验机进行四点弯曲疲劳试验。试验温度为15 ℃，采用应变控制模式。根据SHRP-A303报告的研究成果，试验的结束条件设定为模量减小至初始模量的50%时终止[15]，记录Nf50疲劳次数。同一条件下安排平行试验2次，去除误差大于20%和意外破坏的试件。

由于笔者神经网络所选取的输入变量有沥青含量、空隙率和应变水平3种，因此按照表1的因素水平进行疲劳试验。

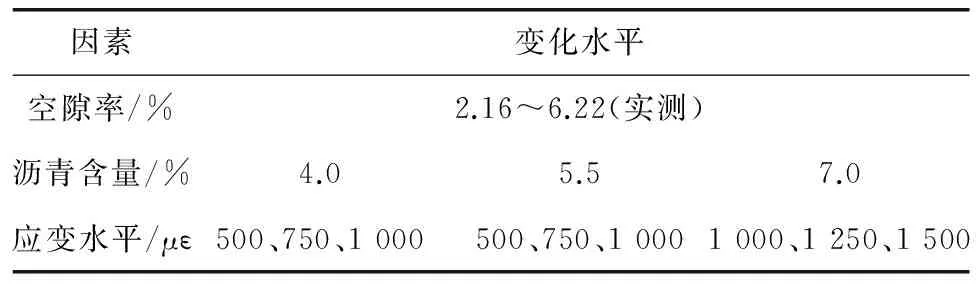
表1 疲劳试验因素水平设置Table 1 Level setting of fatigue test factor

疲劳试验数据如表2，并通过散点图的形式呈现在图1中，图中AC为Asphalt Content编写，表示沥青含量。图1中3个数据系列分别对应了3种沥青含量。

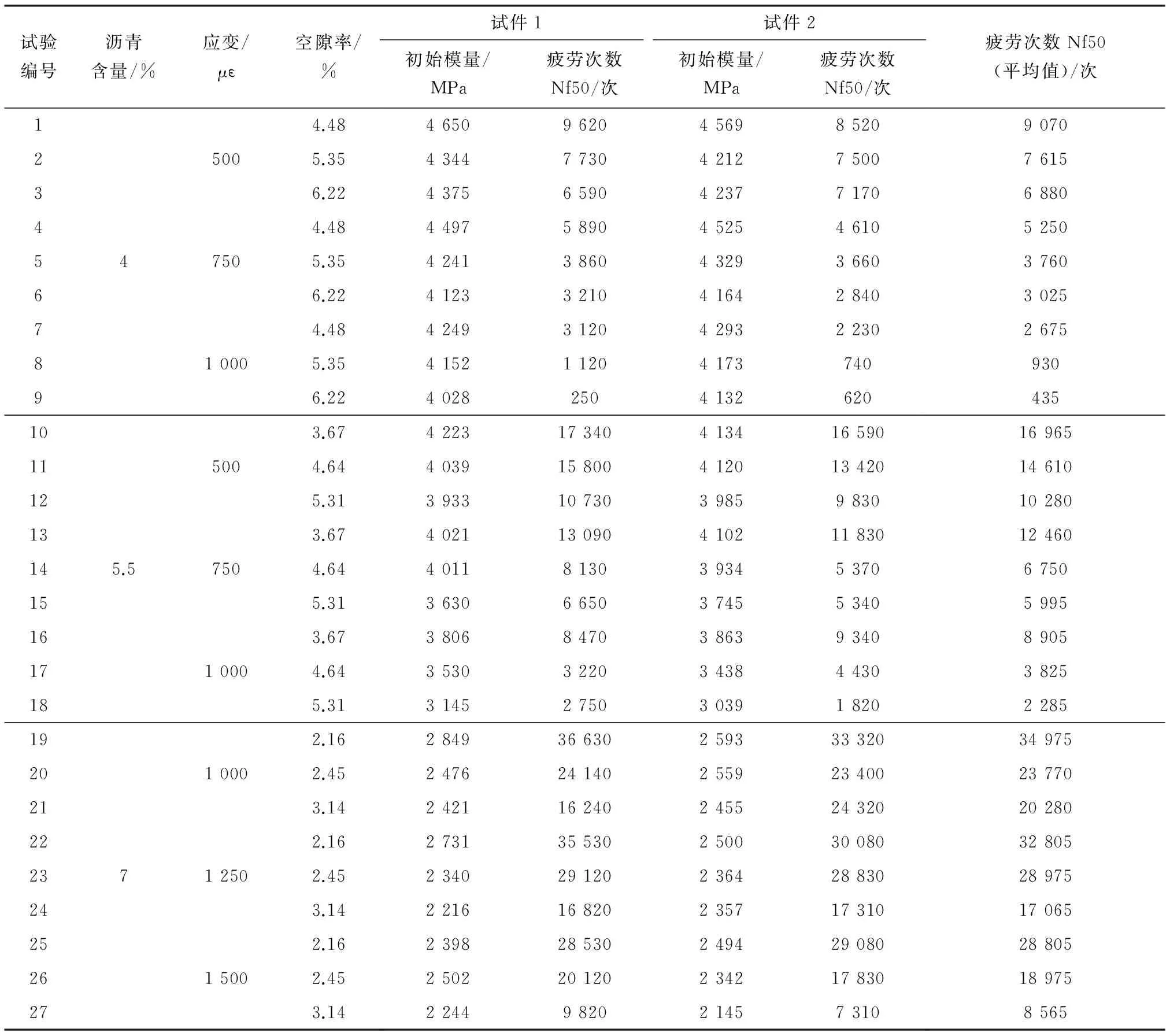
表2 疲劳试验结果Table 2 Fatigue test results

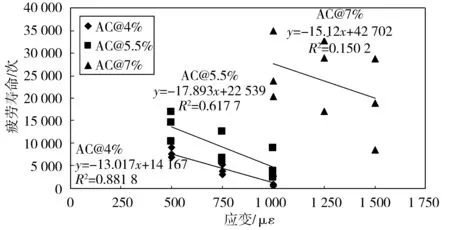
图1 疲劳试验结果Fig. 1 Fatigue test results

由图1可见，沥青含量的变化对疲劳寿命影响显著，使得疲劳结果明显分为3个区域。在不同的区域内，应变水平越高，疲劳寿命越低。沥青含量对疲劳寿命的影响大于应变水平的影响。每一次提高沥青含量，疲劳寿命都会出现跃升，而逐渐提高应变水平，疲劳寿命的变化较为平缓。

为了探讨疲劳寿命的变化规律，在不同沥青含量下对应力和疲劳寿命进行了线性拟合(拟合结果见图1)和单因素方差分析。结果发现随着沥青含量的升高，线性拟合趋势线的斜率变化不大，截距逐渐增加，拟合优度R2则越来越小。这表明在高沥青掺量下疲劳寿命得到明显提升(截距增大)，但是对于应变的敏感程度则逐渐降低(R2越来越小)，同时由于疲劳寿命数量级的提升，变异性越来越大，更容易受到其他因素的影响。

单因素方差分析结果如表3。

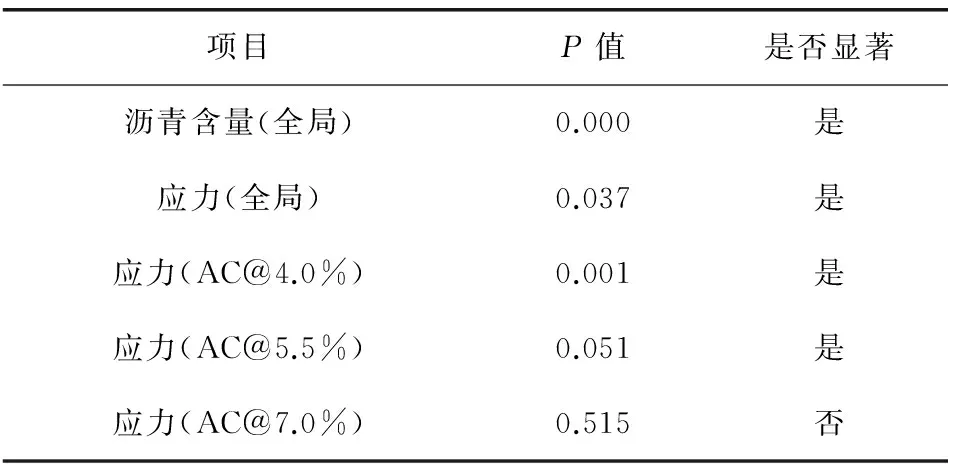
表3 单因素方差分析结果Table 3 ANOVA results

整体来看，沥青含量与应力水平的P值均小于0.05，说明两者对疲劳寿命均有显著性影响。同时沥青含量P值接近于0，显著性明显大于应力水平。对不同沥青含量下的疲劳数据分别计算应力影响的显著性，发现随着沥青含量的升高，应力水平的影响越来越不显著，这与线性拟合趋势线的结果一致，说明高沥青掺量下的疲劳寿命对于应变的敏感程度较低。

3 模型建立与比较

对表2所示的疲劳数据进行处理，每两组平行试验的疲劳寿命Nf50取平均值，从而得到训练所需的27组样本。每一组训练数据包含3个输入值(沥青含量、空隙率、应变水平)和1个输出值(平均疲劳寿命Nf50)。为提高神经网络训练速度，还需要对数据进行归一化处理。

利用MATLAB程序搭建结构如前文所述的神经网络，采用27组训练数据对网络进行训练。训练目标设定为MSE<0.001(此处MSE为归一化后MSE)。当网络训练进行到第70 998次时，训练目标达成，此时网络拟合优度R2达到了0.91。

在MATLAB中使用sim函数，对训练好的神经网络进行仿真操作。网络得出的预测值与真实值的对比如图2。为方便对神经网络的预测效果进行评价，图2将疲劳试验真实值、神经网络预测值以及两者的相对误差3个变量按照不同的样本编号展示于同一张图表中，其中相对误差r为真实值与预测值之差的绝对值除以真实值。

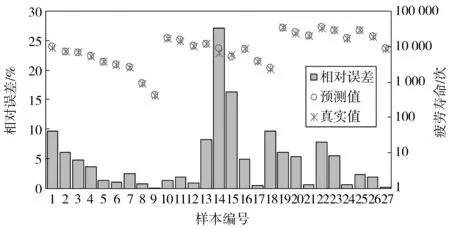
图2 神经网络预测效果Fig. 2 Neural network prediction result

由图2可见，所有的预测值与真实值都几乎完全重叠，这表明神经网络经训练后在整个试验参数区间内都能达到较好的拟合效果，并没有出现过拟合的现象。同时柱状图显示27组数据中，有25组数据的相对误差在10%以内，所有数据的相对误差均在30%以内，这进一步表明神经网络在呈现出整个样本群内在特性的同时，仍能保证对每个单独数据点的预测效果。

为对比预测效果，采用同一组数据对常用的J. T. HARVEY等[4]疲劳方程模型进行拟合，得到疲劳方程，如式(1)：

Nf=1.725×106.79e0.200 6*AC-0.604 2*AVε-0.840 1

(1)

疲劳方程与真实值的相关系数R2为0.83，真实值与预测值的对比如图3。

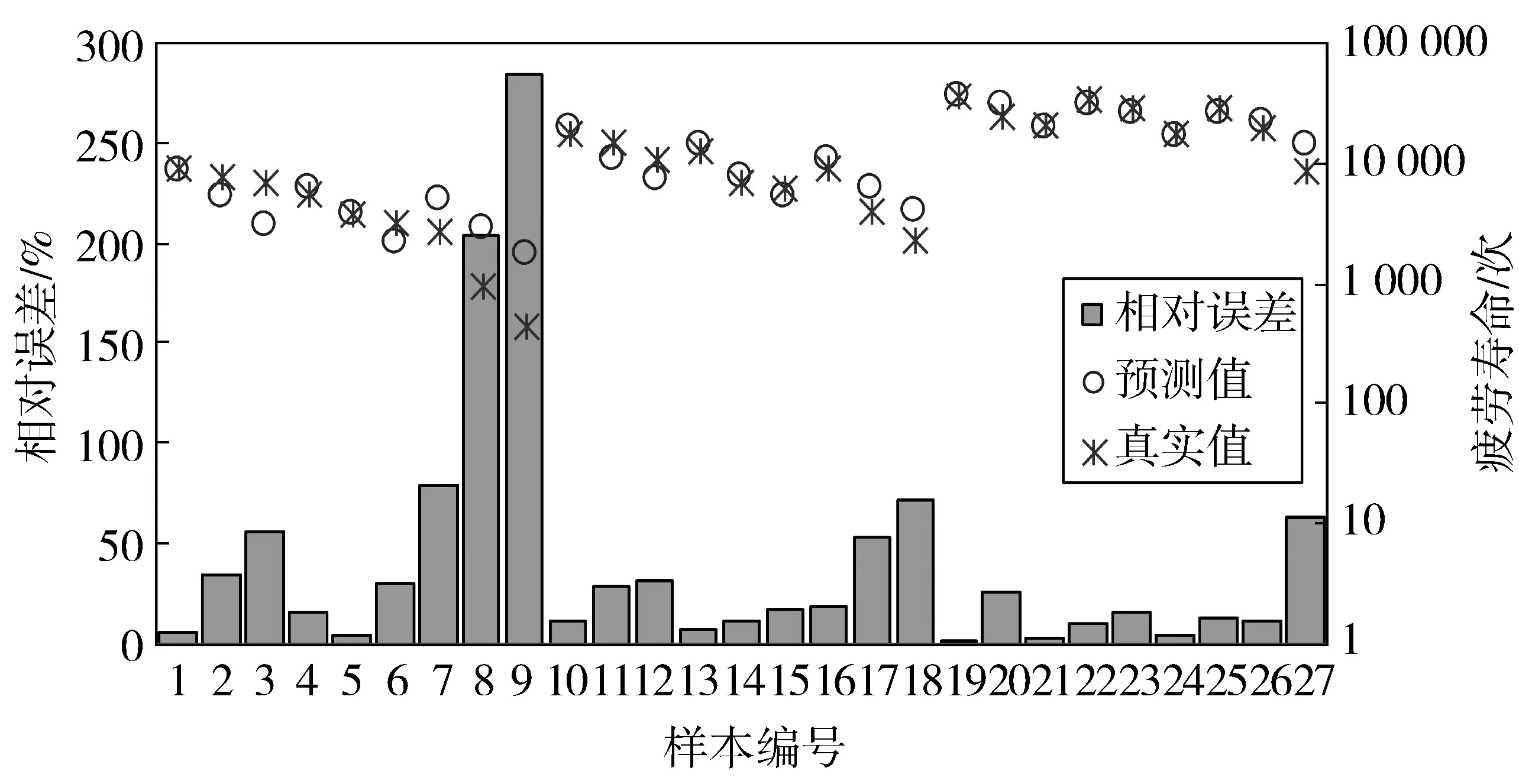
图3 疲劳方程拟合效果Fig. 3 Fitting effect of fatigue equation

由图3可见，回归方程散点图所代表的预测值与真实值并不能很好地重合到一起，各数据点的相对误差明显高于神经网络模型，大部分数据的相对误差在30%左右，有7组数据的相对误差超过了50%，8号与9号样本的相对误差甚至达到了200%以上。

4 预测效果对比

为了量化评价拟合效果，采用数学模型评估中常用的指标 “均方根误差”(Root mean square error以下简称RMSE)进行比较。在有限测量次数中，RMSE常用式(2)计算：

(2)

式中：n为数据个数；di为第i组真实值与预测值的偏差。

RMSE越小，表明拟合效果越好。通过拟合优度、平均相对误差以及RMSE三个指标对两种模型的预测值进行比较，比较结果如表4。由表4可见，神经网络的R2优于疲劳回归方程，RMSE仅为疲劳回归方程的34.9%，同时平均相对误差在5%以下，而疲劳回归方程的平均相对误差则达到了41%。3个指标均显示出神经网络模型拟合效果明显优于疲劳回归方程。

表4 模型拟合效果对比Table 4 Comparison of model fitting effect

神经网络模型还有一个疲劳方程所不具备的优势是可以量化对比不同因素之间的权重[16-19]。由于在学习过程中，网络需要根据实际数据不断调整优化输入层和隐藏层之间的连接权矩阵，已达到模拟数据内在规律的目的，因此其权值的大小在一定程度上反映了指标对结果的影响程度。基于此原理，可以利用训练好的神经网络进行正向推理，通过输入层到隐含层之间的连接权矩阵V计算得到各指标的权重。

各指标的权重ω计算方法如下[16]：

(3)

式中：ωj为第j个输入项的权重；m为输入项个数；k为隐藏层节点个数；vjl为第j个输入项在第l个节点所对应的权值。

在本例中，训练后的神经网络输入层到隐含层连接权矩阵V为

根据式(3)计算可得沥青含量、应变水平、空隙率3个指标的权重分别为：0.435、0.321、0.244。沥青含量对疲劳寿命影响最显著，其次分别为应变和空隙率。这与疲劳试验观察结果一致，说明应用神经网络对疲劳寿命影响因素分析是可行的。

5 结 论

目前国内外有关疲劳寿命预测的研究仍多采用疲劳方程对数据进行回归，拟合效果时有好坏。神经网络是一种诞生于道路工程学科以外的数学模型，笔者尝试将这种新的数据处理方法与传统的沥青混合料试验相结合，以期在混合料疲劳寿命研究领域提供一些新的启发与思路。相关结论如下：

1) 神经网络模型善于处置多变量综合预测问题，且通过调整内部各节点的权值和阈值可以充分逼近任意复杂的非线性关系，具有搭建沥青混合料疲劳寿命预测模型的特质。

2) 混合料疲劳寿命在不同沥青含量下明显分为3个区域。数据分析显示沥青含量对寿命的影响大于应变的影响，高沥青掺量下疲劳寿命得到明显提升，对于应变的敏感程度逐渐降低，变异性逐渐增大。

3) 基于四点弯曲疲劳数据训练的神经网络疲劳寿命预测模型拟合优度R2可达到0.91，在整个样本区间内，预测值与真实值都符合得很好，27组训练数据中，有25组数据的相对误差在10%以内，所有数据的相对误差均在30%以内。神经网络模型在保留样本整体特征的同时，仍能做到对每个数据点实现精确预测。

4) 对比了神经网络模型和传统疲劳方程的预测效果。拟合优度、平均相对误差和均方根误差3个统计指标均显示：相较于传统的疲劳方程预测模型，神经网络预测模型预测效果更为优秀。同时神经网络还可以量化分析指标的权重，分析结果与实际试验结果一致，说明神经网络疲劳寿命预测模型具有参考价值。

[1] JONES D，HARVEY J T，MONISMITH C L.ReflectiveCrackingStudy：SummaryReport[R].UC Berkeley：University of California Pavement Research Center，2007.

[2] QI X，SHENOY A，AL-KHATEEB G.Laboratory characterization and fullscale accelerated performance testing of crumb rubber asphalts and other modified asphalt systems[C]//AsphaltRubberConference.Palm Springs，California：[s.n.]，2006：39-66.

[3] MANGIAFICO S，BENEDETTO H D，SAUZÉAT C，et al.Statistical analysis of the influence of RAP and mix composition on viscoelastic and fatigue properties of asphalt mixes[J].Materials&Structures，2015，48(4)：1187-1205.

[4] MONISMITH C L，LONG F，HARVEY J T.California’s interstate-710 rehabilitation：Mix and structural section designs，construction specifications[J].AsphaltPavingTechnology：AssociationofAsphaltPavingTechnologists-ProceedingsoftheTechnicalSessions，2001，70：762-799.

[5] DONDI G，PETTINARI M，SANGIORGI C，et al.Traditional and Dissipated Energy approaches to compare the 2PB and 4PB flexural methodologies on a warm mix asphalt[J].Construction&BuildingMaterials，2013，47(47)：833-839.

[6] 赵复笑，余天庆，金生吉.沥青路面反射裂缝机理及夹层结构应力分析[J].沈阳建筑大学学报(自然科学版)，2010，26(2)：296-300.

ZHAO Fuxiao，YU Tianqing，JIN Shengji.Experimental study on deformati of multi-level retaining[J].JournalofShenyangJianzhuUniversity(NaturalScience)，2010，26(2)：296-300.

[7] HAFEEZ I，KAMAL M A，MIRZA M W，et al.Laboratory fatigue performance evaluation of different field laid asphalt mixtures[J].Construction&BuildingMaterials，2013，44(7)：792-797.

[8] LI N，MOLENAAR A A A，PRONK A C，et al.Application of the partial healing model on laboratory fatigue results of asphalt mixture[J].Construction&BuildingMaterials，2015，95：842-849.

[9] 李友坤.BP神经网络的研究分析及改进应用[D].合肥：安徽理工大学，2012.

LI Youkun.AnalysisandImprovementApplicationsofBpNeuralNetwork[D].Hefei：Anhui University of Science and Technology，2012.

[10] 谭忆秋，公维强，徐慧宁.基于BP神经网络沥青混合料低温弯拉应变预测模型[J].沈阳建筑大学学报(自然科学版)，2009，25(2)：224-229.

TAN Yiqiu，GONG Weiqiang，XU Huining.Research on the application of neural network in the model for limiting flexural strain of asphalt mixture at low temperature[J].JournalofShenyangJianzhuUniversity(NaturalScience)，2009，25(2)：224-229.

[11] 王震宇.基于BP神经网络的沥青老化预测系统研究[D].重庆：重庆交通大学，2014.

WANG Zhenyu.ResearchonAsphaltAgingPredictionSystemBasedonBPNeuralNetwork[D].Chongqing：Chongqing Jiaotong University，2014.

[12] XIAO F P.DevelopmentofFatiguePredictiveModelsofRubberizedAsphaltConcrete(RAC)ContainingReclaimedAsphaltPavement(RAP)Mixtures[D].South Carolina ：Clemson University，2006

[13] 吴宏宇，熊卫士，张庆明.基于沥青混合料疲劳性能预测的混沌神经网络模型研究[J].公路交通技术，2011(5)：45- 47，53.

WU Hongyu，XIONG Weishi，ZHANG Qingming.Research on chaotic neural network model based on prediction for fatigue performance of asphalt mixtures[J].TechnologyofHighwayandTransport，2011(5)：45- 47，53.

[14] 袁斌，葛折贵，葛折圣.沥青混合料抗疲劳性能的预测模型[J].市政技术，2006，24(1)：31-33.

YUAN Bin，GE Zhegui，GE Zhesheng.Prediction model of asphalt mixtures fatigue properties[J].MunicipalEngineeringTechnology，2006，24(1)：31-33.

[15] FAKHRI M，HASSANI K，GHANIZADEH A R.Impact of loading frequency on the fatigue behavior of sbs modified asphalt mixtures[J].Procedia-SocialandBehavioralSciences，2013，104(3)：69-78.

[16] 张天云，陈奎，魏伟，等.BP神经网络法确定工程材料评价指标的权重[J].材料导报，2012，26(2)：159-163.

ZHANG Tianyun，CHEN Kui，WEI Wei，et al.The determination of index weights for comprehensive evaluation of engineering materials with bp neural network[J].MaterialsReview，2012，26(2)：159-163.

[17] WANG Z L，LI Y C，SHEN R F.Correction of soil parameters in calculation of embankment settlement using a BP network back-analysis model[J].EngineeringGeology，2007，91(2)：168-177.

[18] HE Y，LI X，DENG X.Discrimination of varieties of tea using near infrared spectroscopy by principal component analysis and BP model[J].JournalofFoodEngineering，2007，79(4)：1238-1242.

[19] 马雁军，李建英，张兆同.基于神经网络的农业机械化水平影响因子权重测算和分析[J].中国制造业信息化(学术版)，2006，35(5)：74-77.

MA Yanjun，LI Jianying，ZHANG Zhaotong.The factors weight measurement and analysis of agricultural mechanization level affect with bp neural network[J].ManufacturingInformationEngineeringofChina，2006，35(5)：74-77.