X-Gorenstein 投射复形

杨晓燕,杜代国

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

0 引言

2010年,Bennis等[1]引入了X-Gorenstein投射模的概念.设X是包含所有投射模的模类，称模M是X-Gorenstein投射模,如果存在投射模的正合序列

P=…→P1→P0→P0→P1→…,

其中M≌Im(P0→P0),使得对任意的F∈X,HomR(P,F)正合.他们证明了X-Gorenstein 投射模类是投射可解的.Meng等[2]进一步研究了X-Gorenstein投射模,并对X-Gorenstein投射维数进行了刻画.若X是所有投射模构成的类,则X-Gorenstein投射模就是Enochs 和 Jenda引入的Gorenstein投射模[3].1998年,Enochs等[4]把Gorenstein投射模的概念推广到了复形范畴,引入并研究了Gorenstein 投射复形的同调性质.若X是所有平坦模构成的类,则X-Gorenstein投射模就是Ding投射模[5-6].Yang等[7]把Ding投射模的概念推广到了复形范畴,研究了Ding 投射复形的同调性质.若X是所有 Level 模构成的类,则X-Gorenstein投射模就是Gillespie引入的 Gorenstein AC-投射模[8].Bravo等[9]研究了复形范畴中的Gorenstein AC-投射对象,讨论了这类复形与其各层次的模之间的关系.

受以上文献的启发,文中引入X-Gorenstein投射复形,给出了X-Gorenstein投射复形的同调刻画,证明了X-Gorenstein 投射复形构成的类是投射可解的以及X-Gorenstein 投射复形的类关于直和项和直和是封闭的.

1 预备知识

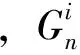
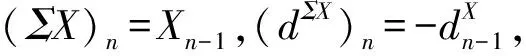
设X,Y是链复形,用Hom(X,Y)表示由X和Y确定的Abel群复形:

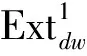
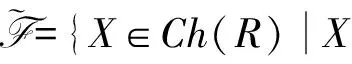
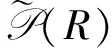
2 主要结论

定义2设X是包含所有投射复形的复形类,称复形M是X-Gorenstein投射复形.如果存在投射复形的正合序列

P=…→P-2→P-1→P0→P1→…,

其中M≅Im(P-1→P0),使得对任意的F∈X,Hom(P,F)正合.

引理1设X是包含所有投射复形的复形类.若F∈X且M是X-Gorenstein投射复形,则对任意n≥1有Extn(M,F)=0.

证明由X-Gorenstein投射复形的定义可知,存在复形的正合序列

…→P-2→P-1→M→0,

其中Pi是投射的.所以有复形正合序列

故对任意的n≥1有Extn(M,F)=0. 】

引理2设X是包含所有投射复形的复形类,则M是X-Gorenstein投射复形当且仅当存在Hom(-,X)-正合的正合右投射分解0→M→P0→P1→…,且对任意的F∈X,有

Ext≥1(M,F)=0.

证明必要性.由X-Gorenstein投射复形的定义和引理1可得.

充分性.考虑M的投射分解…→P-2→P-1→M→0.因为对任意的F∈X有Ext≥1(M,F)=0,所以上述投射分解是Hom(-,X)-正合的.因此我们有Hom(-,X)-正合的投射复形的正合列

…→P-2→P-1→P0→P1→P2→…,

使得M≅Ker(P0→P1).故M是X-Gorenstein投射复形. 】

定理1设X是包含所有投射复形的复形类,则X-Gorenstein投射复形的类是投射可解类.

证明显然投射复形是X-Gorenstein投射复形.考虑正合序列0→X→Y→Z→0,其中Z是X-Gorenstein投射复形.若X是X-Gorenstein投射复形,则X,Z存在Hom(-,X)-正合的正合右投射分解

于是有如下行和列正合的交换图:

因为第一列和第三列是Hom(-,X)-正合的,所以第二列是Hom(-,X)-正合的.又因为对任意F∈X有Ext≥1(X,F)=0=Ext≥1(Z,F),所以由长正合列引理可知Ext≥1(Y,F)=0.故由引理2可知,Y是X-Gorenstein投射复形.

假设Y是X-Gorenstein投射复形,则有复形正合序列0→Y→P→Y′→0,其中P是投射复形,Y′是X-Gorenstein投射复形.考虑下列推出图:

因为Z和Y′是X-Gorenstein投射复形,所以H是X-Gorenstein投射复形.于是存在 Hom(-,X)-正合的正合右投射分解

设F∈X,因为Z和Y是X-Gorenstein投射复形,由长正合列引理可知Ext≥1(X,F)=0，所以X存在Hom(-,X)-正合的正合右投射分解

由引理2可知,X是X-Gorenstein投射复形. 】

命题1设X是包含所有投射复形的复形类,则X-Gorenstein投射复形的类关于直和项和直和封闭.

证明设{Xλ}λ∈Λ是一簇X-Gorenstein投射复形,则对任意λ∈Λ,Xλ存在Hom(-,X)-正合的正合右投射分解

于是可得Hom(-,X)-正合的⊕λ∈ΛXλ的正合右投射分解

因为对任意F∈X,Ext≥1(⊕λ∈ΛXλ,F)≅∏Ext≥1(Xλ,F)=0,所以由引理2可知⊕λ∈ΛXλ是X-Gorenstein投射复形.

设X是X-Gorenstein投射复形且X=Y⊕Z.下证Y是X-Gorenstein投射复形.由上述证明可知X-Gorenstein投射复形类关于直和封闭.现假设W=Y⊕Z⊕Y⊕Z⊕….注意到W≅X⊕X⊕…是X-Gorenstein投射复形.因为W≅Y⊕W,所以Y⊕W也是X-Gorenstein投射复形,于是可得可裂短正合序列

0→Y→Y⊕W→W→0，

其中W和Y⊕W是X-Gorenstein投射复形.由定理1可知Y是X-Gorenstein投射复形. 】

命题2设X是包含所有投射复形的复形类,0→X→Y→Z→0是复形正合列.若X和Y是X-Gorenstein投射复形,则Z是X-Gorenstein投射复形当且仅当对任意F∈X有Ext1(Z,F)=0.

证明必要性显然,下证充分性.因为X是X-Gorenstein投射复形,所以存在复形的正合列0→X→P→G→0,其中P是投射复形,G是X-Gorenstein投射复形.于是有推出图:

在短正合列0→Y→H→G→0 中,因为G和Y是X-Gorenstein投射复形,所以由定理1知,H是X-Gorenstein投射复形.又因为复形P∈X,所以Ext1(Z,P)=0.从而第二行的正合列可裂，故由命题1知,Z是X-Gorenstein投射复形. 】

P=…→P-2→P-1→P0→P1→…,

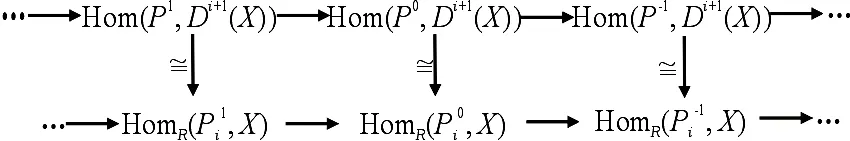
于是下行也正合.所以对任意的模X∈X,用HomR(-,X)作用投射模序列

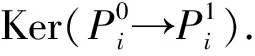
引理4设M,F是复形.若对任意的n∈Z,Ext1(M,ΣnF)=0,则Hom(M,F)正合.

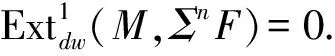
证明对任意的同态f′:M→P′,其中P′是投射模,定义α=(f,f′):M→P⊕P′.有正合列

⊕P′→Coker(α)→0.

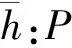
证明必要性由引理3和引理4可得.

充分性.已知对任意的i∈Z,Mi是X-Gorenstein投射模.由文献[1]命题2.2可知存在短正合序列0→Mi→Xi→Ni→0,其中Xi是投射模,Ni是X-Gorenstein投射模.设

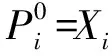
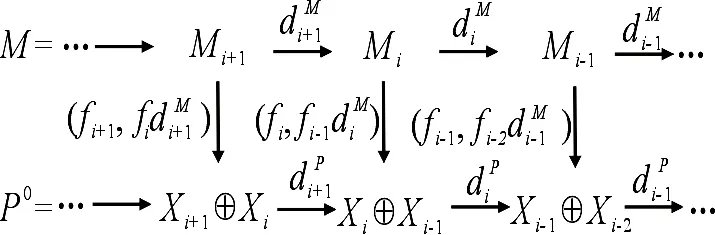
易知α是单的,且有复形短正合序列

0→Zj(F)→Fj→Zj-1(F)→0

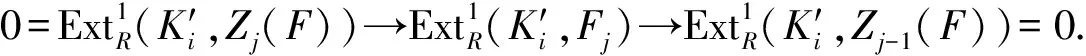
是正合的.于是可得正合序列

0→M→P0→P1→…,

0→K-1→P-1→M→0,

…→P-2→P-1→M→0,

[1] BENNIS D,OUARGHI K.X-Gorenstein projective modules[J].InternationalMathmaticalForum,2010,5(10):487.

[2] MENG F Y,PAN Q X.X-Gorenstein projective and Y-Gorenstein injective modules[J].HacettepeJournalofMathmaticsStatistics,2011,40(4):537.

[3] ENOCHS E E,JENDA O M G.Gorenstein injective and projective modules[J].MathZ,1995,220:611.

[4] ENOCHS E E,ROZAS J R.Gorenstein injective and projective complexes[J].CommAlgebra,1998,26(5):1657.

[5] DING N Q,LI Y L,MAO L X.Strong Gorenstein flat modules[J].JAustMathSoc,2009,86:323.

[6] GILLESPIE J.Model structures on modules over Ding-Chen rings[J].Homology,Homotopy,App,2010,12(1):61.

[7] YANG G,LIU Z K,LIANG L.Module structures on categories of complexes over Ding-Chen rings[J].CommAlgebra,2013,41:50.

[8] GILLESPIE J.Gorenstein complexes and recollements from cotorsion pairs[J].AdvMath,2016,291:859.

[9] BRAVO D,GILLESPIE J.Absolutely clean,level,and Gorenstein AC-injective complexes [J].CommAlgebra,2016,44:2213.

[10] GILLESPIE J.The flat model structure on Ch(R)[J].TransAmerMathSoc,2008,356(8):3369.