28 GHz下对毫米波透射特性的分析

刘蕾 田磊 陈旭彬 唐盼 张建华

(1. 教育部泛网无线通信重点实验室，北京 100876； 2. 网络与交换技术国家重点实验室，北京 100876)

引 言

随着高速传输数据需求不断增长,推动了未来移动通信系统中毫米波段的应用. 随着诸如空间波束成形,高增益自适应天线和多输入多输出(Multiple-Input Multiple-Output,MIMO)等先进技术的发展,毫米波通信系统模型得到了进一步的发展[1-4]. 然而,由于衍射、反射和散射损耗较大,所以周围环境对毫米波的通信质量影响很大. 想要发展毫米波技术,就需要深入了解毫米波信道的传播特性.

有两种常用的方法来进行毫米波信道建模. 一种是基于传统的实际测量,另一种是基于使用电磁场理论的仿真. 近年来,基于几何光学原理的射线追踪(Ray-tracing)方法由于其简单和计算高效的优点得到了越来越多的关注[5-6]. 然而,在不同的入射角、极化方式、材料和粗糙度的情况下,透射、反射、衍射和散射的典型参数不足,射线追踪法因为计算复杂度的限制,较难进行多次反射、衍射和散射的模拟,而且该方法对环境复杂度的要求较高,在较为杂乱的环境下难以得到精确的信道预测结果. 因此,当接收机检测到多径分量,或者信号受到两次及以上的衰减的时候,传统的测量更准确.

在过去的几十年中,进行了一些关于在28 GHz,38 GHz,60 GHz和73 GHz的毫米波信道传播特性的研究[7-11]. 文献[12]通过考虑不同室内和室外材料对穿透损耗的影响,得到透明玻璃的穿透损耗约为3.9 dB. 此前在文献[13]中提出的测量结果表明,当无线信号透过透明玻璃时,穿透损耗可以忽略不计,而玻璃被金属涂层覆盖时,其穿透损耗显著提高了25 dB至50 dB. 文献[14]根据对典型墙壁、地板和窗户的透射系数的分析,描述了多层电介质模型. 文献[15]研究了入射角、介质材料的折射率和厚度对透射系数的影响. 文献[16]讨论了任意层状介质中电磁波的透射系数. 石灰石和砖墙的粗糙表面散射特性见文献[17].

在此前诸多学者的研究工作中主要考虑在透射测量中,不同入射角、材料粗糙度对透射系数的影响,但是仍有一些影响透射系数的情况没有被充分地考虑到.为了提供毫米波信道的更为准确的参数,

我们考虑了不同的入射角、垂直和水平极化以及发射端(Transmitter,Tx)和接收端(Receiver,Rx)之间的不同距离对系数的影响,在28 GHz高频频点下的玻璃门两侧处进行了透射测量.

本文将测量数据进行处理并与光滑表面和高斯粗糙表面的菲涅耳传播定律模型进行了对比. 观察透射系数与不同入射角、极化方式、材料粗糙程度和收发端距离的关系. 从而为第5代移动通信(The 5th Generation,5G)毫米波透射特性研究的进一步发展提供参考与帮助.

1 测量准备和测量方法

1.1 测量准备

在测量中,使用800 MHz带宽的信号探测仪来捕获信道数据. 在Tx侧,首先生成长度为511的伪随机序列,然后信号通过上变频器调制到28 GHz,使用功率放大器将其功率增加到30 dBm. 采用一对25 dBi喇叭天线,水平方向的3 dB波束宽度为10°,垂直方向的为11°. 在Rx侧,低噪声放大器可以放大接收信号,保证高信噪比(Signal Noise Ratio,SNR). 接着下变频器将接收到的信号解调为基带信号. 采样率是原始伪噪声(Pseudo-Noise,PN)序列的3倍,延迟分辨率约为0.833 ns,PN序列的整个持续时间为1.28 μs. 测量系统的参数总结在表1中.

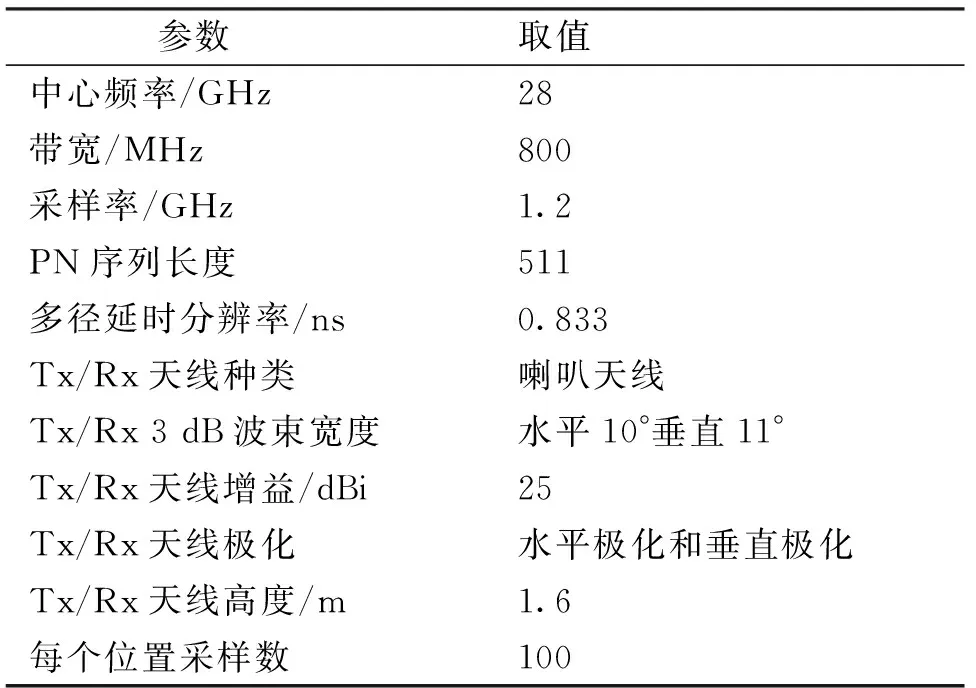
表1 测量系统参数

我们在北京邮电大学教三楼玻璃门两端进行了测量. 玻璃门由厚度为1.1 cm的透明玻璃制成. 如图1所示,Tx侧是户外环境,Rx侧是室内环境.

图1 测量环境

1.2 透射测量规划

为了获得精确的透射系数,在99个Tx-Rx位置和99个视距(Line-of-Sight,LOS)路径位置在玻璃门两侧进行了28 GHz的测量,用玻璃门打开时的接收信号作为参考. 为了研究不同极化方式,收发端距离和入射角对穿透特性的影响,我们设计了三种测量场景.

1.2.1 角度和极化对穿透特性影响

如图2所示,Tx和Rx按照所需要的入射和接收角度相向放置在玻璃门的两侧. 发射和接收天线采用水平(垂直)极化方式.θe和θt分别代表入射角和透射角.dt和dr分别表示TX和RX到玻璃门的距离. 在我们的测量中,远场距离设置为2.4 m,可以通过式(1)计算:

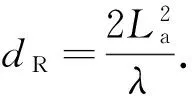
(1)

式中:La是天线的最大尺寸,为11 cm;λ是电磁波的波长.

在测量中,dt和dr都设为2.5 m,入射角从0°开始每隔5°测量一次,直到80°. 透射系数可以由不同入射角和不同极化方式的测量数据计算得到.

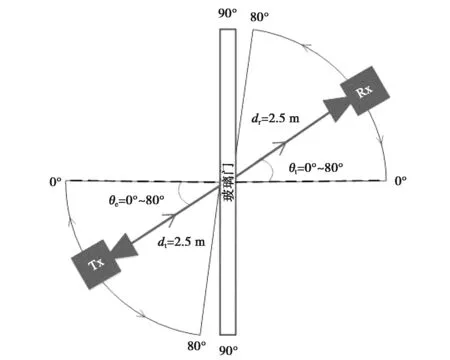
图2 探究不同入射角和极化方式对透射系数影响的测量示意图

1.2.2 距离对透射特性影响

为了研究距离对透射性能的影响,将Tx和Rx放置在玻璃门的两侧,并放置在一条线上． 图3和图4提供了测量示意图.dt和dr同时从0.4 m增加到3.5 m,间隔为0.1 m,入射角设为0°和45°.

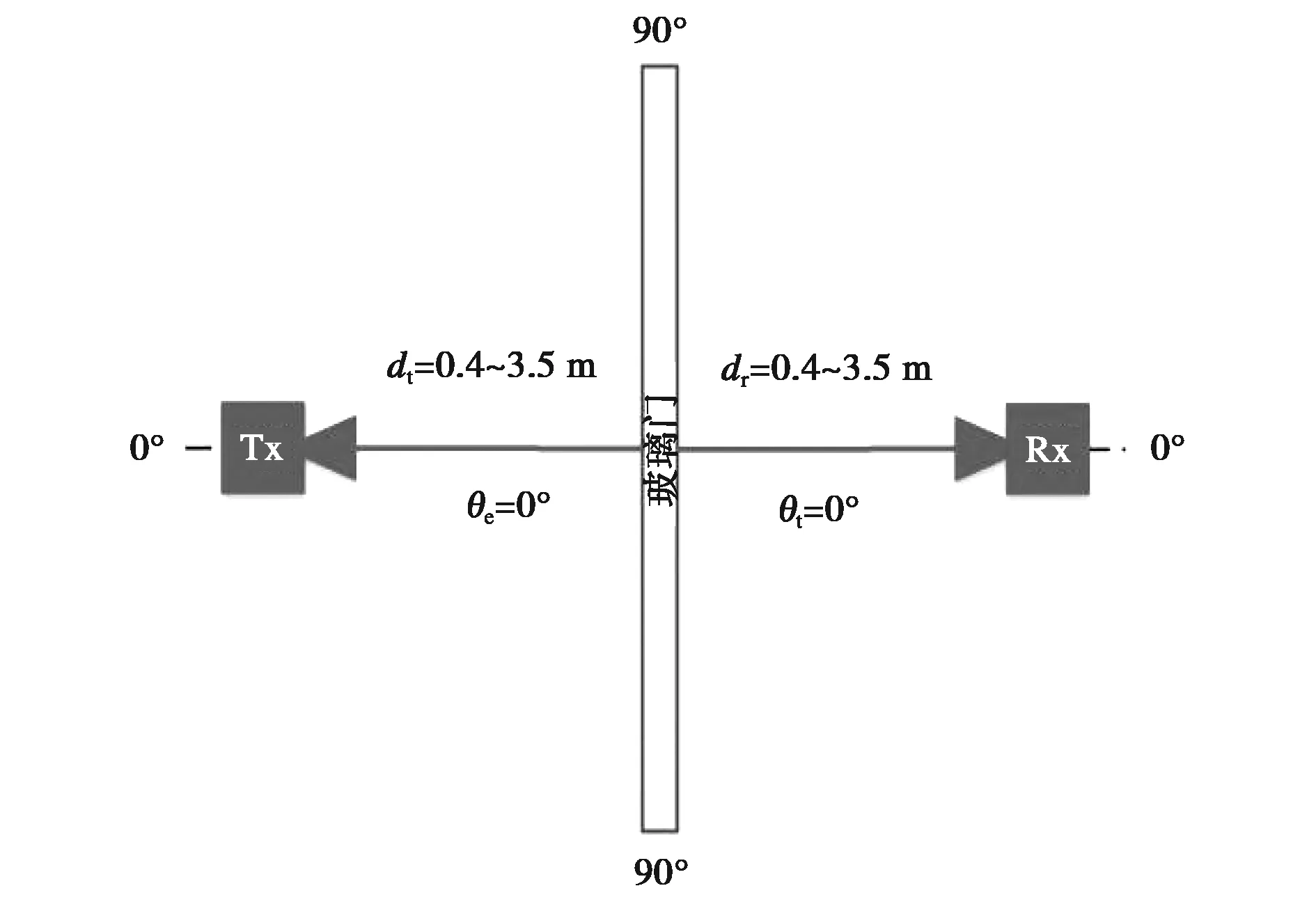
图3 0°入射角下探究不同Tx-Rx距离对透射系数影响的测量示意图

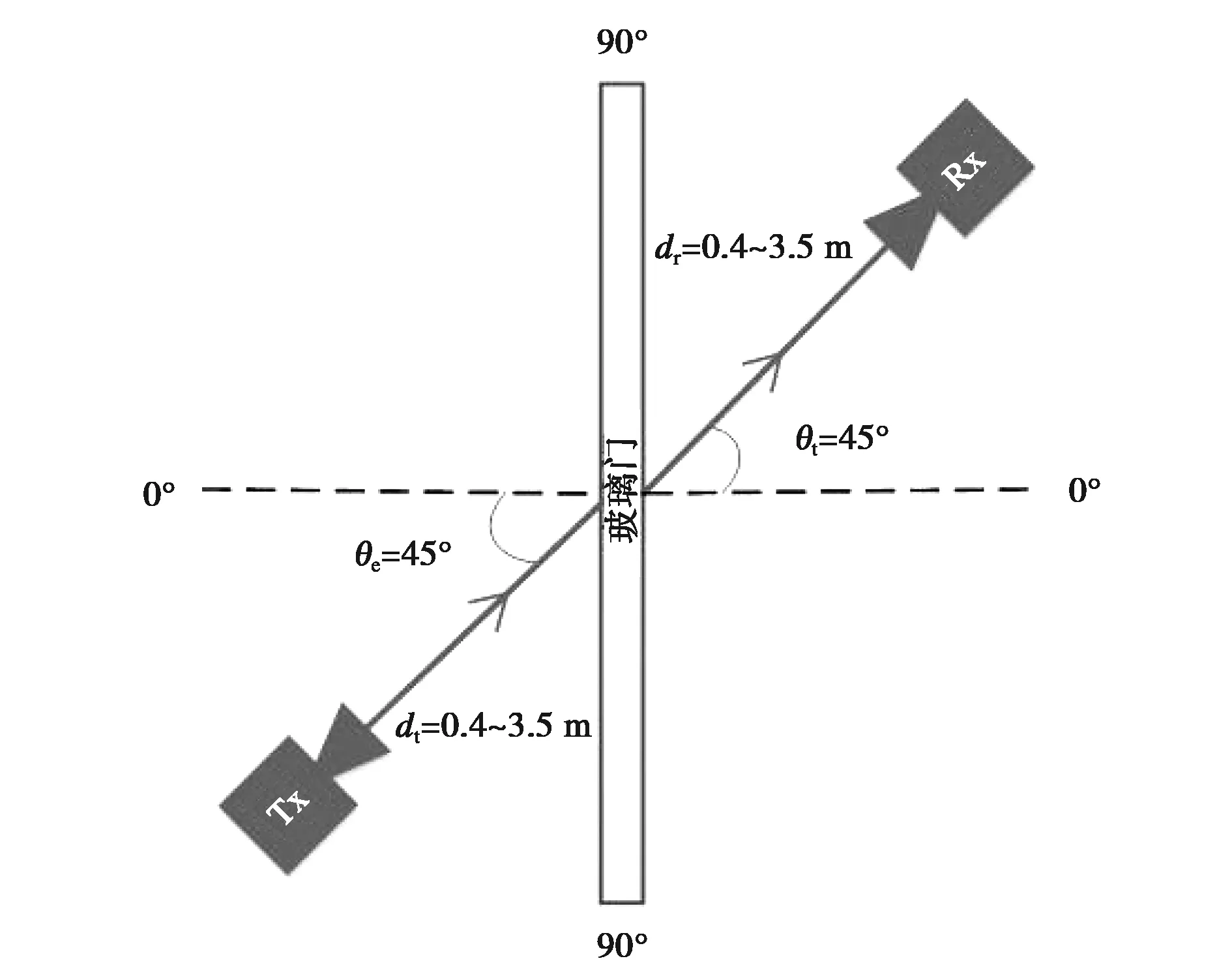
图4 45°入射角下探究不同Tx-Rx距离对透射系数影响的测量示意图

2 数据处理

2.1 透射系数

2.1.1 电介质半空间的透射系数

当电磁波照射在光滑的表面上时,著名的菲涅尔透射因子可用于描述穿透特性.定律中考虑了材料类型,入射角和极化类型.该材料的特征可以由复介电常数表示:

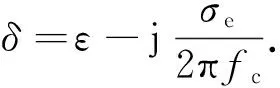
(2)

式中:介电常数ε=ε0εr;σe是导电率;fc是载波频率.

斯涅尔定律描述了入射角与电磁波的反射角之间的关系为θr=θe,透射角由式(3)给出:

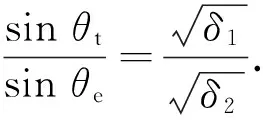
(3)

式中:θr,θe和θt分别是反射角,入射角和透射角;δ1和δ2分别是介质的复介电常数. 透射系数可以由文献[18]计算为:

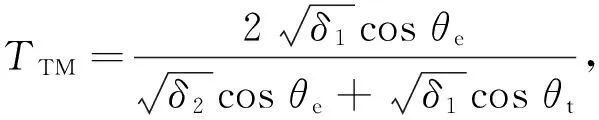
(4)

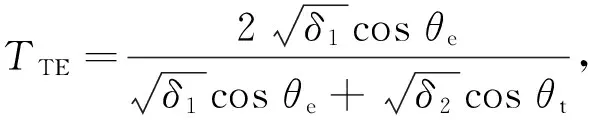
(5)

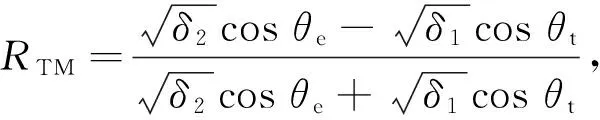
(6)

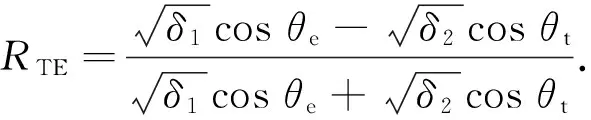
(7)

式中:TM表示横向磁性,磁场分量平行于边界;TE是横向电场情况,电场分量平行于边界. 在测量中,垂直极化是由TE描述的,而水平极化则由TM描述.

2.1.2 分层电介质的透射系数

式(4)、(5)中的透射系数仅考虑到电介质半空间的一个电介质界面.但实际的测量场景则是介电层两侧被空气所包围,需要考虑波穿过介电层的透射问题.所以总透射系数可以由部分波之和给出[18]:

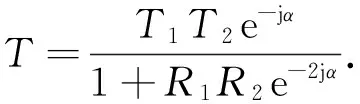
(8)

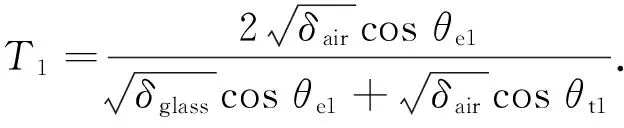
(9)

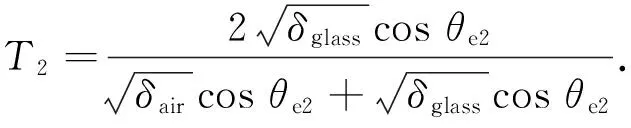
(10)

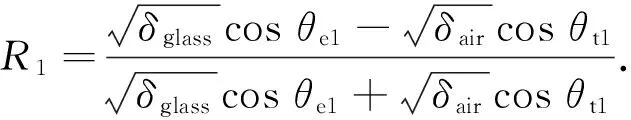
(11)

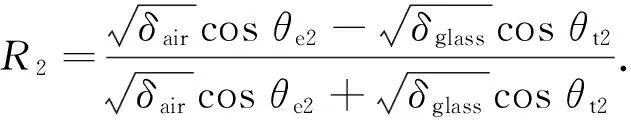
(12)

式中,θe1,θt1和θe2,θt2分别指从空气到玻璃的入射角和透射角及从玻璃到空气的入射角和透射角.同理,垂直极化的透射系数T1和T2可以由式(5)得到,反射系数R1与R2由式(7)计算.

2.1.3 散射情况下的透射系数

式(8)的透射系数仅考虑表面光滑的镜面穿透情况.当电介质的表面不是理想光滑时,粗糙的表面会导致散射现象,从而减小了透射波的功率.对于粗糙表面的情况,存在散射损耗因子ρs[19]:

(13)

式中,σh是表面高度和平均表面高度的偏差. 因为散射的损耗也会影响透射系数,所以我们考虑到可以通过粗糙表面的散射损耗因子ρs来修改如式(8)表达的透射系数的理论公式. 所以本文最终提出的透射系数模型Trough为

Trough=ρsT.

(14)

2.2 数据处理方法

测量结束之后,原始数据用于计算透射系数:

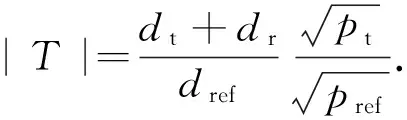
(15)

式中:pt是接收到的透射功率;而pref是接收到的参考功率. 接收功率可以由RX端收集的IQ原始数据计算出来.

3 测量结果与分析

测量分析中电介质界面的典型性质如下:玻璃的相对介电常数为εr=8 F/m;真空介电常数ε0=8.854×10-12F/m;相对磁导率μr=1 H/m;28 GHz时玻璃门的电导率为σe=0.23 S/m[19].

透射系数由公式(15)计算可得,使用玻璃门打开时的接收功率作为参考. 图5和图6描绘了垂直和水平天线极化方式下透射系数的结果.

在图5中,当入射角从0°增加到80°时垂直极化的透射系数从0.8减小到0.25. 图6给出了水平极化的透射系数结果: 总体趋势是一开始保持稳定,随着入射角度不断增大,透射系数随之逐渐增大,当入射角为70°左右时达到最大值,入射角继续增大至70°和80°之间时透射系数有所减小; 高斯粗糙表面模型计算出的透射系数比65°入射角时的测量结果大0.1.

对比图5和图6中两种天线极化方式的透射系数的结果,发现水平极化的透射系数要比垂直极化的大,而且水平极化的透射系数随角度增大而稳定地小幅增长再回落,而垂直极化的透射系数随角度增大而呈现明显递减趋势．

理想光滑表面与高斯粗糙面模型透射系数的比较结果也在图5和图6中给出. 由于测试玻璃表面有厚度偏差σh=0.3 mm,导致理想光滑表面的预测结果和高斯粗糙表面模型之间有细微的差异. 通过计算测量所得数据与两种模型之间的方差,结果发现在垂直和水平两种极化方式下测量数据与高斯粗糙表面模型更为拟合.

考虑到天线的方向图和远场情况,我们也研究了不同距离对穿透特性的影响. 如图7所示,透射场景下的接收功率随距离的变化趋势与LOS场景的结果一致. 在比较LOS和穿透的接收功率后,我们得出结论:0°入射角时的穿透损耗在2.63 dB和3.23 dB之间;而当入射角为45°时,穿透损耗范围在5.16～5.91 dB之间.

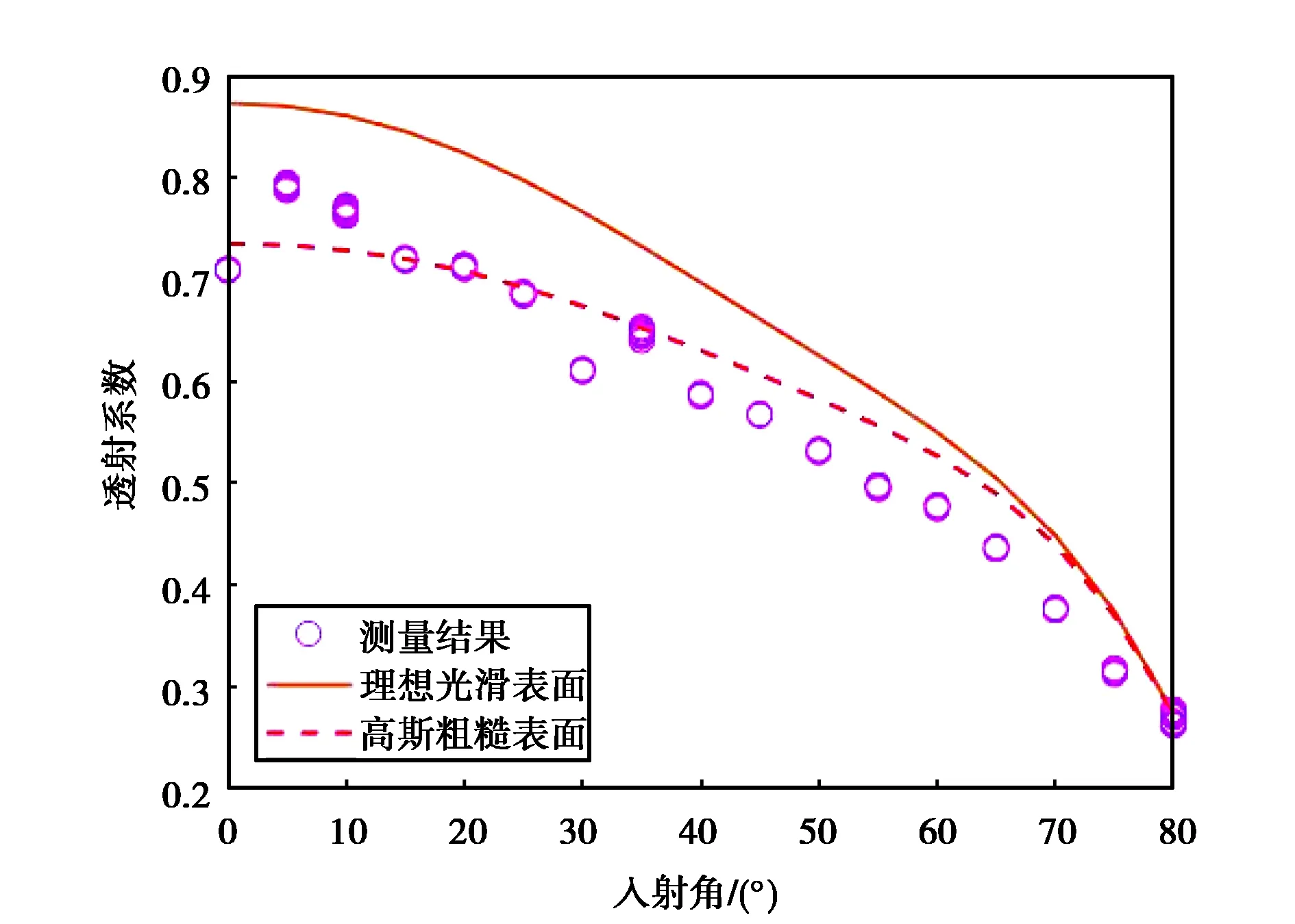
图5 测量结果与理论垂直极化的透射系数对比

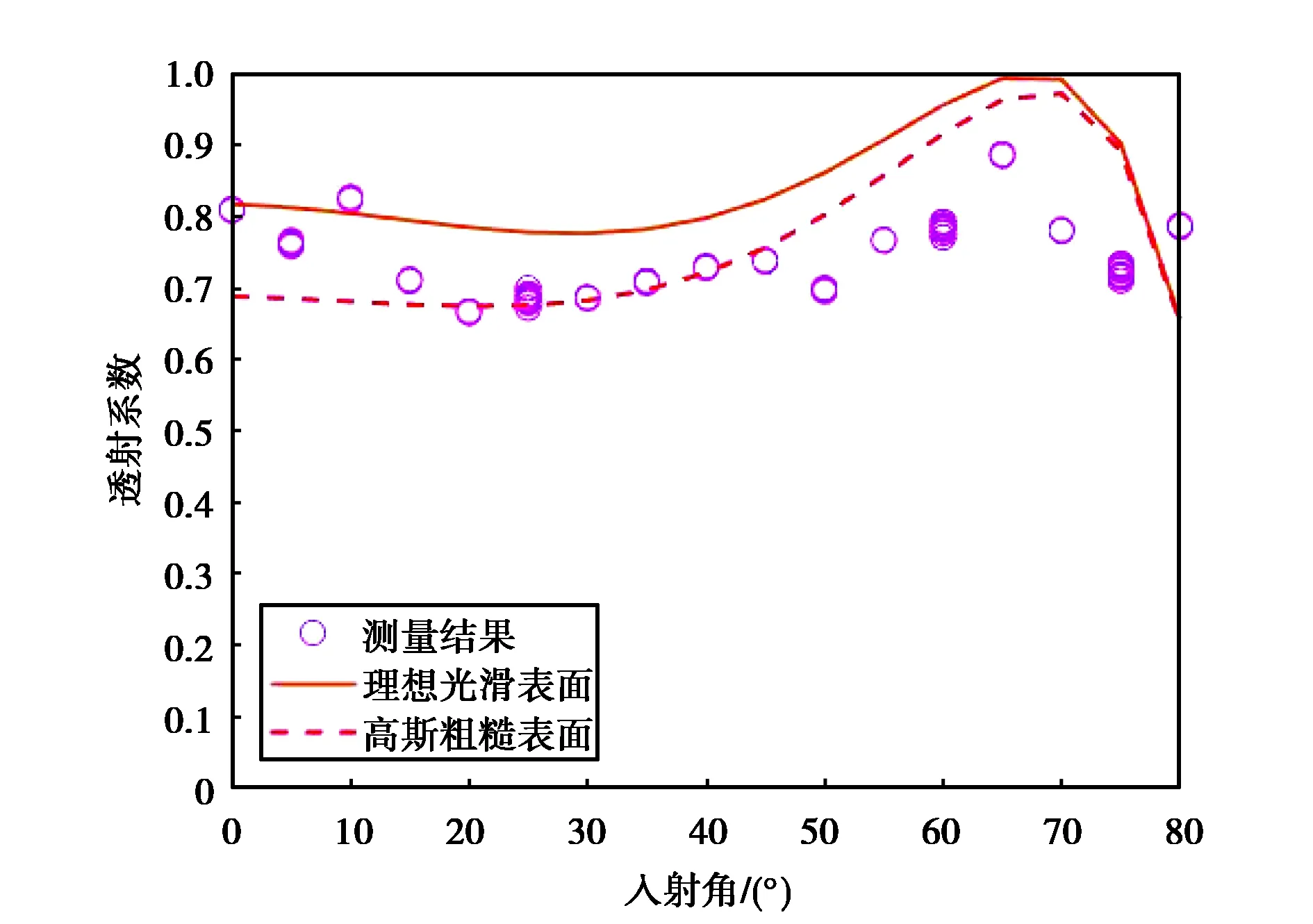
图6 测量结果与理论水平极化的透射系数对比

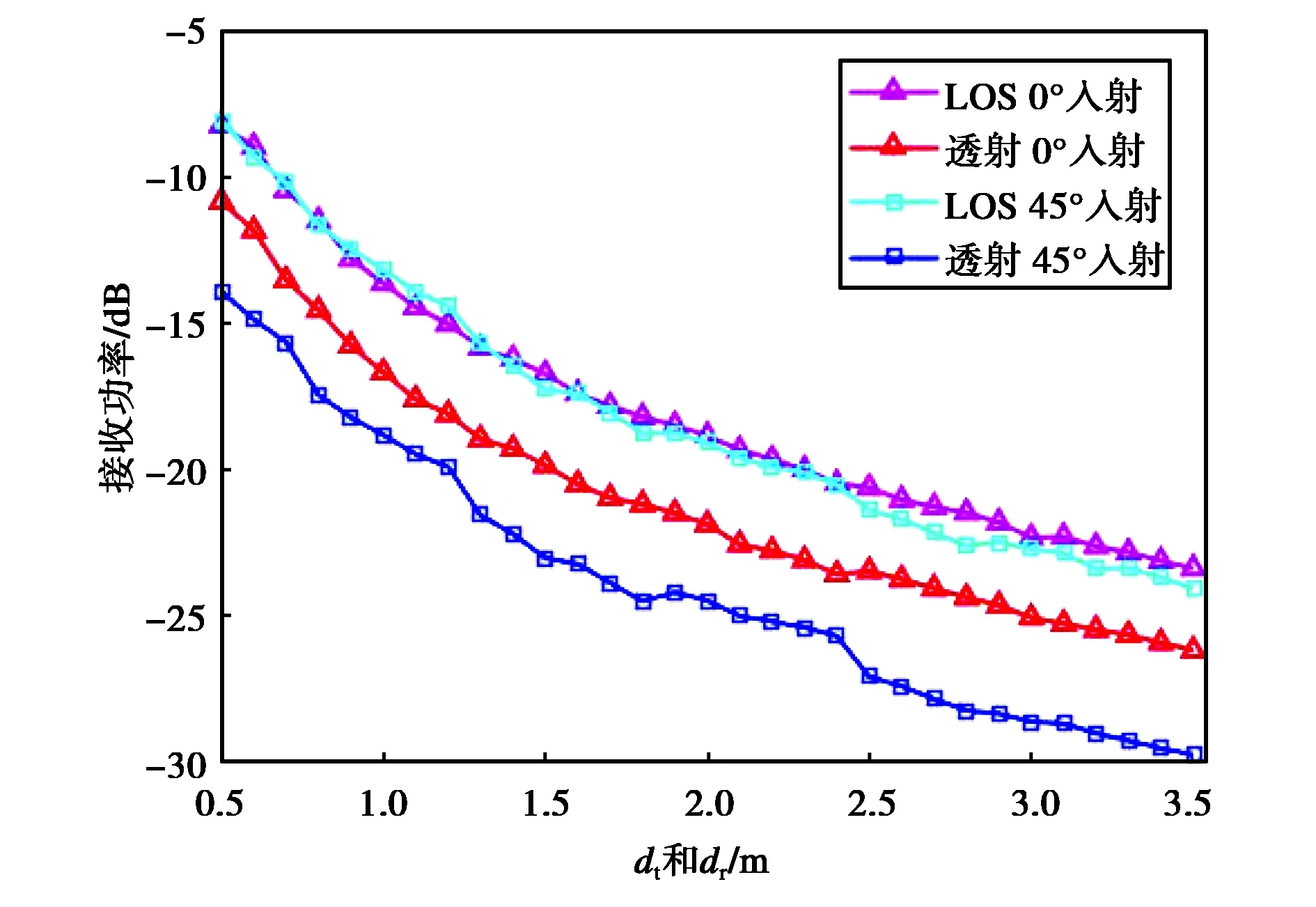
图7 穿透特性与距离关系(dt和dr表示Tx和Rx到玻璃门的距离)

4 结 论

本文使用垂直极化和水平极化的天线在28 GHz

的频点下进行了对玻璃门透射系数的测量. 然后将测量数据与式(8)的理想光滑表面模型和式(14)提出的高斯粗糙表面模型进行比较. 本文给出了玻璃门的准确透射系数,这些系数是我们用不同入射角和不同天线极化方式测量的数据分析得出的. 为了验证分析结果的准确性,将测量数据与菲涅尔公式的理论结果进行比较. 虽然光滑表面的菲涅耳公式和高斯粗糙面菲涅耳公式都与测量数据趋势相同,但结果表明,透射系数均可以与高斯粗糙面菲涅尔公式进行精确建模与拟合. 此外,还分析了不同入射角下的穿透损耗,研究了测量结果与对数距离模型的联系.

本文在前人对透射研究的基础之上更加深入地研究了入射角度、天线极化方式及收发端之间距离对透射性能的影响,并给出了每种测量变量下的透射系数值,同时与理想光滑表面及高斯粗糙表面两种模型进行对比验证. 这些分析结果都为毫米波系统的未来发展提供了参考和帮助.

[1] PI Z Y, KHAN F. An introduction to millimeter-wave mobile broadband systems[J]. Communications Magazine, 2011, 49(6): 101-107.

[2] RAPPAPORT B T S, MURDOCK J N, GUTIERREZ F. State of the art in 60-GHz integrated circuits and systems for wireless communications[J]. Proceedings of the IEEE, 2011, 99(8): 1390-1436.

[3] GUTIERREZ Jr F, AGARWAL S, PARRISH K, et al. On-chip integrated antenna structures in CMOS for 60 GHz WPAN systems[J]. IEEE journal on selected areas in communications, 2009, 27(8): 1367-1378.

[4] CHEN X, TIAN L, TANG P, et al. Modelling of human body shadowing based on 28 GHz indoor measurement results[C]//2016 IEEE 84th Vehicular Technology Conference, 2016: 1-5.

[5] 柳文, 王俊江, 焦培南, 等. 电离层三维射线追踪的快速计算方法[J]. 电波科学学报, 2009, 24(1): 55-59.

LIU W, WANG J J, JIAO P N, et al. A fast ray tracing algorithm in the ionosphere[J]. Chinese journal of radio science, 2009, 24(1): 55-59.(in Chinese)

[6] NAGY L. Comparison and application of FDTD and ray optical method for indoor wave propagation modeling[C]//Proceedings of the Fourth European Conference on Antennas and Propagation. Barcelona, 12-16 April, 2010: 1-3.

[7] RAPPAPORT T, MACCARTNEY G R, SAMIMI M, et al. Wideband millimeter-wave propagation measurements and channel models for future wireless communication system design[J]. IEEE transactions on communications, 2015, 63(9): 3029-3056.

[8] KYRO M, RANVIER S, KOLMONEN V M, et al. Long range wideband channel measurements at 81—86 GHz frequency range[C]//2010 Proceedings of the Fourth European Conference on Antennas and Propagation, 2010: 1-5.

[9] XU D, ZHANG J H, GAO X X, et al. Indoor office propagation measurements and path loss models at 5.25 GHz[C]//2007 IEEE 66th Vehicular Technology Conference, 2007: 844-848.

[10] HUANG F S, TIAN L, ZHENG Y, et al. Propagation characteristics of indoor radio channel from 3.5 GHz to 28 GHz[C]//2016 IEEE 84th Vehicular Technology Conference, 2016: 1-5.

[11] HANEDA K, JARVELAINEN J, KARTTUNEN A, et al. A statistical spatio-temporal radio channel model for large indoor environments at 60 and 70 GHz[J]. IEEE transactions on antennas and propagation, 2015, 63(6): 2694-2704.

[12] ZHAO H, MAYZUS R, SUN S, et al. 28 GHz millimeter wave cellular communication measurements for reflection and penetration loss in and around buildings in New York city[C]//2013 IEEE International Conference on Communications, 2013: 5163-5167.

[13] VIOLETTE E J, ESPELAND R H, DEBOLT R O, et al. Millimeter-wave propagation at street level in an urban environment[J]. IEEE transactions on geoscience and remote sensing, 1988, 26(3): 368-380.

[14] SATO K, MANABE T, IHARA T, et al. Measurements of reflection and transmission characteristics of interior structures of office building in the 60-GHz band[J]. IEEE transactions on antennas and propagation, 1997, 45(12): 1783-1792.

[15] 文盛乐, 易慧先. 电磁波以任意角入射时介质层的透射系数[J]. 湖南师范大学自然科学学报, 1999, 22(3): 56-59.

WEN S L, YI H X. Medium-jransmissivity of the electromagnetic wave injected with arbitrary incident angle[J]. Acta Scientiarum Naturalium Universitatis Normalis Hunanensis, 1999, 22(3): 56-59.(in Chinese)

[16] 周琦, 刘新芽. 多层介质中电磁波的反射与透射[J]. 南昌大学学报, 2003, 27(1): 41-43.

ZHOU Q, LIU X Y. The reflection and transmission of electromagnetic wave in multilayer media[J]. Journal of nanchang university(natural science), 2003, 27(1): 41-43.(in Chinese)

[17] DILLARD C L, GALLAGHER T M, BOSTIAN C W, et al. Rough surface scattering from exterior walls at 28 GHz[J]. IEEE transactions on antennas and propagation, 2004, 52(12): 3173-3179.

[18] 拉帕波特. 无线通信原理与应用[M]. 周文安, 等译. 北京: 电子工业出版社, 2006: 79-93.

[19] 莫利斯. 无线通信[M]. 田斌, 等译. 北京:电子工业出版社, 2008: 37-50.