数字锁相放大器中相敏检测技术的基本原理实验

陈泽宁，王自鑫，贺子芸，贾莲莲，陈弟虎，蔡志岗

(中山大学 a.物理学国家级实验教学示范中心;b.电子与信息学院;c.物理学院，广东 广州 510275)

锁相放大器[1]是专用于检测微弱信号[2]的电学仪器. 如今，微弱信号检测在科研领域中愈发重要，稳定的高精度数字锁相放大器对微弱信号的检测起到至关重要的作用[3-4]. 数字锁相放大器可在强噪声背景下提取出微弱信号，且具有抗干扰能力强、大幅提高信号信噪比、动态范围大、时间稳定性强等特点，这得益于相敏检测技术(phase sensitive detection, PSD). PSD中的核心参量(时间常量、陡降、动态储备)对微弱信号的测量结果和测量精度有重要影响.

1 实验原理

1.1 锁相放大器的基本原理

锁相放大技术是基于互相干方法的微弱信号检测手段，其核心是PSD. PSD把与待测微弱信号具有相同频率和固定相位关系的参考信号作为基准，通过一系列乘法运算和滤波处理提取出有用信号. 在锁相放大器中，PSD由相敏检测器实现.

相敏检测器最基本的含义即将输入信号相乘的乘法器，可分为数字相敏检测器和模拟相敏检测器[4]. 相敏检测器模块与低通滤波器(low-pass filter, LPF)模块的组合如图1所示.

图1 相敏检测器模块和低通滤波模块图

输入待测信号SI(t)可定义为

SI(t)=AIsin (ωt+φ)+B(t),

(1)

其中AIsin (ωt+φ)是待测目标信号，幅值为AI，角频率为ω，相位为φ,B(t)是总噪声.

与输入待测信号有固定频率关系的参考信号SR(t)可定义为

SR(t)=ARsin (ωt+δ).

(2)

2路信号同时输入乘法器，输出信号为

B(t)ARsin (ωt+δ),

(3)

(3)式由3部分组成:从时域上看，第1部分包含待测信号幅值AI、参考信号幅值AR和待测信号与参考信号的相位差(φ-δ)的余弦值. 这部分在输入信号和参考信号稳定的情况下为定值，即直流信号. 第2部分为参考信号二倍频交流信号. 第3部分为噪声信号与参考信号的相乘结果. 一般，由于随机信号与完备的正弦信号无相关性，第3部分在时域上的积分结果通常为零.

从频域上看，第1部分为直流信号. 第2部分为二倍频信号. 第3部分为经过一倍频频谱搬移的噪声信号，例如假设原噪声信号为白噪声，经过ω频谱搬移，结果仍为白噪声信号.

提取输入信号的幅度AI是微弱信号领域中处理的核心问题. 由式(3)可知，式中只有第1部分和第2部分与AI有关. 由于测量直流信号的精度、难度以及可靠性通常远比测量高频信号的高，锁相放大器常通过在乘法器模块后加低通滤波器模块提取出第1部分的直流信号，再做进一步的处理.

理想状态下，S0(t)通过低通滤波器可完全滤除二倍频信号，其结果可表示为

(4)

由于已知参考信号的幅度AR，只要确定相位差(φ-δ)，即可确定输入信号幅度AI. 本文通过2路相位相差90°的PSD通路相互耦合解决相位差问题，这种结构叫做双相相敏检测器结构.

以双相锁相放大器[5-6]OE1022[7]为例，其基本结构由参考通道、信号通道、PSD模块和LPF模块构成，如图2所示.

图2 锁相放大器OE1022结构图

待测信号SI(t)定义同式(1). 两路参考信号可定义为

SR0(t)=ARsin (ωt+δ),

(5)

SR1(t)=ARcos (ωt+δ).

(6)

待测信号和参考信号同时进入PSD模块，经过LPF0和LPF1的滤波后，得到输出为

(7)

(8)

通过X与Y的平方根计算可以得到原输入信号的幅值与相位信息,即

(9)

(10)

1.2 不同时间常量、陡降和动态储备参量的影响

相敏检测器后端的LPF的通带带宽可通过设置时间常量实现，时间常量τC的计算公式为

(11)

式中f为低通滤波器-3 dB处的频率值. 增加τC会减小LPF的带宽，从而在滤除高频信号的同时滤除更多的噪声信号，减小输入端噪声对输出信号的影响，使输出结果更加稳定. 不过，若τC过大，也可能会导致直流分量衰减，使得实验结果不够精准.

相敏检测器后的LPF的形状也与陡降有关. 在同样时间常量下，LPF陡降越大，LPF衰减带越窄，但通带和阻带的纹波越大，输出结果的稳定性越差，输出波动越大. 实际测量中，通常需要将陡降和时间常量一起考虑，选择适中的陡降和时间常量.

对于动态储备(dynamic reserve, DR)的定义，首先需要定义总放大倍数Atotal. 以OE1022为例，如图3所示，PSD前端模拟前置放大器对输入信号进行放大，此放大系数称为前置放大系数A1. 在LPF后端，数字直流放大器对LPF的直流输出信号进行放大，此放大系数称为后置放大系数或直流放大系数A2. 两者放大系数之积为锁相放大器的总放大倍数Atotal.

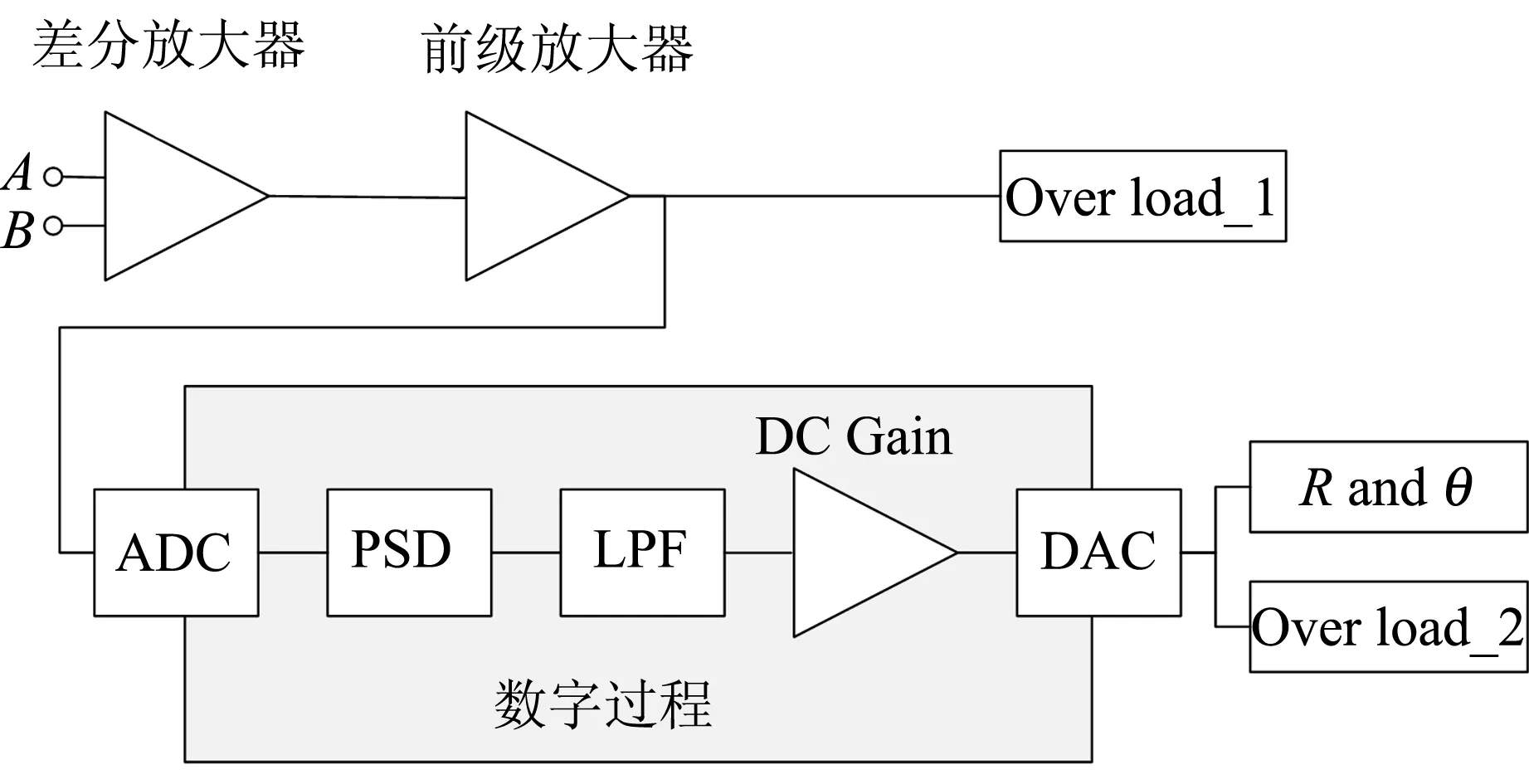
图3 锁相放大器部分内部结构图

NDR表示锁相放大器抵抗噪声和干扰的能力，量纲为dB，可定义为

(12)

其中VFS表示满刻度输出时的输入电平或者满刻度灵敏度，用来表征锁相放大器测量灵敏度，与系统总放大倍数有关，通常以V为单位，可定义为

(13)

其中VOmax表示输出端口(Randθ)的最大幅度，一般是定值. Overload_2即为有用信号输出电压过载的标志. 在这种情况下，VFS只与Atotal有关. 例如输出管脚的VOmax为10 V，系统的Atotal为105，则系统的，VFS为0.1 mV. 换句话说，VFS限制了锁相放大器的输入有用信号的最大范围.

注意：“满刻度输出”中的“输出”表示输入有用信号经过锁相放大器2次放大之后的输出电平；“输入电平”表示输入有用信号在锁相放大器输入端的输入电平.

式(12)中的VOVL(Overload)表示锁相放大器任一级(例如PSD输入级、直流放大器输出级)出现过载或临界过载时的信号电平. 考虑到锁相放大器通常处理的是信噪比较低的输入信号，因此在VFS合适的情况下，过载电压往往是出现在前置放大器输出级的尖锋噪声电压，即Overload_1处. 这些噪声电压将在LPF处滤除. 因此VOVL通常理解为锁相放大器允许的最大输入噪声电压电平有效值，即系统最大的噪声容限.

由上述分析可知，NDR即为锁相放大器的输入端信噪比，表明锁相放大器分辨噪声的能力. 若NDR=100 dB，即表示系统能容忍的输入噪声信号电平可比输入有用信号高105倍. OE1022给出3种DR的选择:Low, Normal, High，对应3种前置放大倍数. 改变不同的动态储备，就是改变前置放大倍数.

在锁相放大器中调整动态储备的公式为

(14)

式中Voverload指的是前置放大器的输出信号额定电压，一般为定值. Overload_1即为噪声信号电压过载的标志.

通常锁相放大器默认设置DR为Normal状态. 假设VFS和Voverload不变，在DR为High时，A1减小，Atotal不变，则A2增大，此时前置放大器与PSD模块之间的AD转换器的噪声相对经过微小放大的输入噪声信号更加明显，即本底噪声会更加明显. 反之，在DR为Low时，A1增大，Atotal不变，则A2减小，此时输入噪声信号会更加明显. 实际测量中，通过衡量本底噪声和输入噪声信号的重要性决定DR的设置参量.

2 实验设计与操作

2.1 实验平台搭建

教学实验平台[8-9]由1台高精度数字锁相放大器OE1022和1台示波器组成，如图4所示.

图4 教学实验平台

实验前，首先要进行OE1022的系统复位操作，接着设定OE1022的SINE OUT端产生有效值为50 mV、频率为1 kHz的正弦波. 该正弦信号会作为待测信号输入到锁相放大器，锁相放大器采用内部参考模式测量该正弦信号的大小R，同时输出该正弦信号经过Atotal放大和全波整流的正弦波至示波器.

OE1022的SINE OUT输出端连接到锁相放大器的信号输入端，OUTPUT输出端连接到示波器的输入端. 连接完成后，即可开始改变实验参量，记录实验数据等.

2.2 实验流程

实验改变时间常量、陡降、动态储备，通过观察OE1022的输出结果和示波器的波形分别评估其对OE1022输出结果精度的影响. 实验中时间常量可选设置为10 μs，30 μs，100 μs，300 μs，…，30 s；动态储备可选设置为Low，High，Normal；陡降可选设置为6 dB/oct，12 dB/oct，18 dB/oct，24 dB/oct.

从实验原理可知，时间常量是影响滤波特性的关键参量. OE1022有多种可选时间常量值，使用者可根据所需实验精度自由选取. 一般实际测量中，时间常量设置需要适中，如果时间常量过小，输出结果中除待测信号外还包含二倍频信号和噪声等高频信号. 相反如果时间常量太大，由于截止频率点离直流点很近，直流量容易受到一定程度的衰减.

考虑到实验的可行性，实验仅选择较有代表性的几个时间常量值. 陡降和动态储备则设置完全. 完整的控制变量实验参量设置如表1.

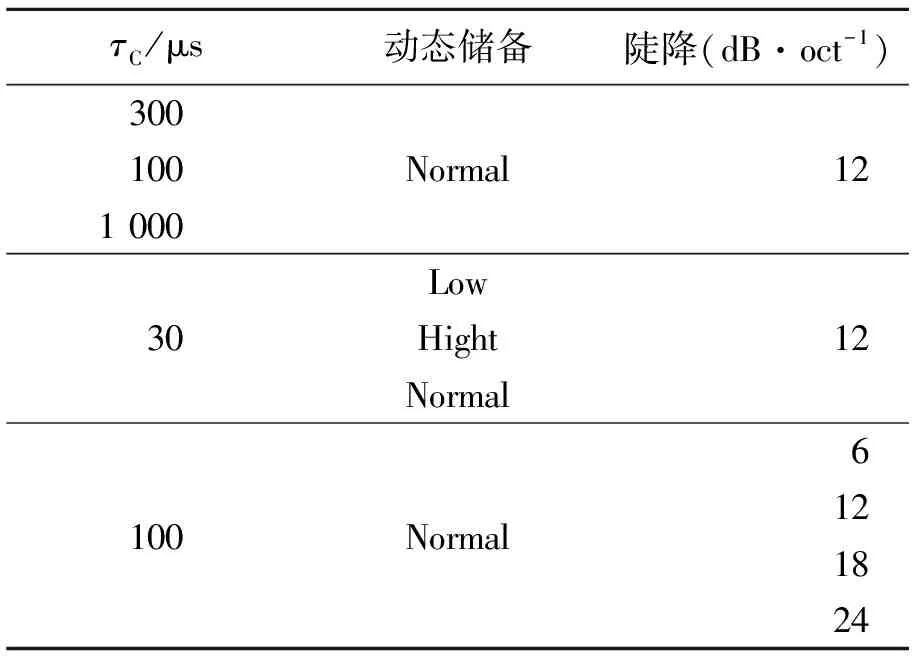
表1 锁相放大器滤波特性影响实验参量设置表

3 实验现象及分析

3.1 时间常量对锁相放大器滤波特性的影响

本组实验中，陡降固定为12 dB/oct，动态储备固定为Normal. 时间常量分别取30 μs,100 μs和1 ms，对应锁相放大器测量输出R值的范围分别为57～63 mV,50～53 mV和50.52～50.56 mV. 由式(9)可知，输入信号通过锁相放大器最终应得到直流量输出. 而此实验指出，不同时间常量得到了3种不同的输出结果：当时间常量为30 μs时，输出信号是经过全波整流的正弦波,如图5(a)所示；当时间常量为100 μs时，输出信号是一直流量叠加一完整正弦波，如图5(b)所示；当时间常量为1 ms时，输出信号仅为一直流量，如图5(c)所示.

(a)30 μs

(b)100 μs

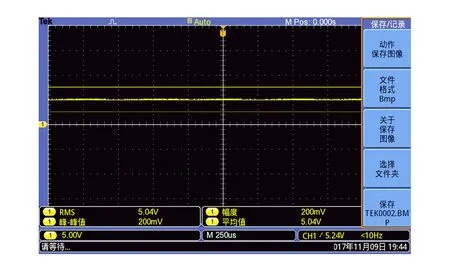
(c)1 ms图5 不同时间常量下通过示波器观测到的波形

由实验原理可知，PSD模块输出结果中，只有二倍频信号sin (2ωt+φ)完全被滤除，才能得到式(9)的结果. 假如二倍频信号成分没有完全被滤除，输出结果应为

(15)

其中对二倍频信号的滤除效果定义为参量α，α为0～1的数，α越大，滤除效果越差.

当α=1时，二倍频完全没有被滤除，输出结果为

R0(t)=2AI|sin (ωt+φ)|,

(16)

为整流后的一倍频正弦波，与图5(a)相符；当0<α<1时，二倍频被部分滤除，输出结果如式(15)，为直流量叠加小幅度二倍频正弦波，与图5(b)相符；当α=0时，输出结果如式(9)，为一直流量，与图5(c)相符.

当时间常量为30 μs，100 μs，1 ms时，由式(11)可以计算，LPF带宽分别为5.31 kHz，1.59 kHz，159 Hz. 30 μs时二倍频(2 kHz)信号完全未被滤除，100 μs时对二倍频(2 kHz)信号的衰减只有4.5 dB，而1 ms时对二倍频衰减有18.1 dB. 因此时间常量为1 ms时，结果受二倍频影响最小. 同时带宽减小，噪声信号的等效噪声带宽也会减小，对测试结果的影响减小.

综上所述，时间常量的影响主要体现在对二倍频信号的滤除效果上. 在其他条件不变的情况下，时间常量越大,LPF的带宽越小，测量结果受二倍频信号和噪声信号的干扰越小，测量结果越准确.

3.2 陡降对锁相放大器滤波特性的影响

本组实验中，时间常量固定为100 μs，动态储备固定为Normal. 陡降分别取6，12，18，24 dB/oct，对应锁相放大器测量输出R值的范围分别为53～57 mV，51～53 mV，50～52 mV，50～51 mV，如图6所示.

根据示波器显示图形进行分析，主要分为2个方面：

1)随LPF陡降的增加，示波器显示的图形幅度逐渐减小，具体表现为波峰降低，波谷升高. 从实验原理中可以知道，当时间常量固定时，LPF陡降增加，会使得其衰减带变窄，越来越多的高频信号会被LPF滤除，输出信号的幅值变小，因此示波器的波形幅度会减小.

(a)6 dB/oct

(b)12 dB/oct

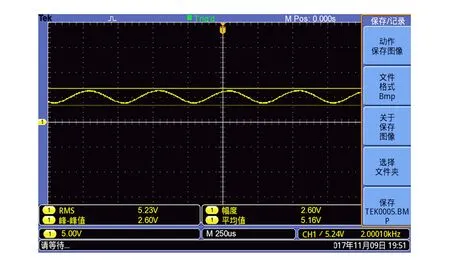
(c)18 dB/oct

(d)24 dB/oct图6 不同陡降下通过示波器观测到的波形

2)实验过程中，增加LPF陡降，观察到示波器波形的抖动加剧. 根据实验原理，实验过程中时间常量保持不变，LPF陡降的增大会导致其衰减带变窄，通带和阻带的纹波会变大，输出波形波动变大.

3.3 动态储备对锁相放大器滤波特性的影响

本组实验中，时间常量固定为30 μs，陡降固定为12 dB/oct. 动态储备分别设置取Normal,Low,High，对应锁相放大器测量输出R值的范围均在53～57 mV，如图7所示.

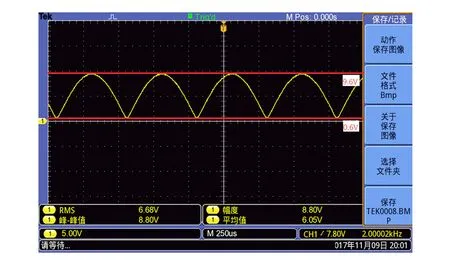
(a)Low

(b)Normal

(c)High图7 不同动态储备下通过示波器观测到的波形

实验过程中逐渐增加动态储备，可以发现波形的幅度会随之增大，同时边缘逐渐出现较多毛刺. 这表明动态储备的改变影响了输出噪声，而且是动态储备越大，输出噪声越多. 根据实验原理可知，锁相放大器改变动态储备是通过调整模拟程控放大器模块的前置放大倍数. 当动态储备为High时，前置放大倍数变小，则进入PSD模块的外部输入噪声变小，因此系统本身的噪声变得不能忽略，例如模数转换模块的噪声、所有信号源的本底噪声等，这些便会使PSD提取信号的过程中掺杂噪声. 如果噪声很大，在高动态储备测量时就会产生较大的测量误差. 如果外部输入噪声比较小，可以通过提高动态储备和直流增益来减小输出误差.

4 结束语

随着现代科学技术的发展，科研探索和实验研究当中经常需要测量物理量的微小变化[9]. 锁相放大器是微弱信号检测领域的一项领先技术，在实际工作环境中已应用于多种场合，比如测量地磁场中光泵磁力仪研制、光学镀膜厚度监控、可调谐二极管激光吸收光谱分析技术、声光调制等. 对于有志于从事科学研究的学生来说，简单了解锁相放大器的原理以及掌握其基础操作是非常必要的. 本文详细介绍了锁相放大技术中处于核心位置的PSD，并针对3个关键参量：时间常量、陡降、动态储备设计了基本原理实验. 完成实验有助于熟悉锁相放大器的基本操作，分析处理实验数据和示波器波形更有利于提高对锁相放大技术原理的理解.

[1] 中国科学院物理研究所微弱信号检测小组. 锁相放大器——一种检测微弱信号的手段[J]. 物理, 1977,6(4):206-210.

[2] 聂娅琴. 基于锁相放大器的微弱信号检测研究[D]. 长沙：中南大学,2014.

[3] 孙志斌,陈佳圭. 锁相放大器的新进展[J]. 物理,2006,35(10):879-884.

[4] 胡华,钟洁. 新型锁相放大器的设计[J]. 电子测量技术,2014,37(8):15-18.

[5] 蔡屹. 基于双相锁相放大器的微弱信号矢量测量[J]. 微计算机信息,2007,23(9-1):111-112,228.

[6] 朱晓莉,厉霞. 基于AD630的双相锁相放大器设计[J]. 机电工程技术,2012,41(6):19-23.

[7] 中大科仪. OE1022数字锁相放大器说明书[EB/OL].http://www.ssi-instrument.com/keyi/suoxiangfangdaqixilie/2016011910.html,20171020.

[8] 王鑫,孙明,张恩杰,等. 锁定放大器原理及应用实验的教学探讨[J]. 物理实验,2002,22(1):41-43.

[9] 黄松筠,何焰兰,丁道一. 微弱信号检测实验教学研究[J]. 物理实验,2003,23(4):23-25.