空间滤波的实验研究

于雪冰，王 伟

(东北师范大学 a.物理学院;b.物理学国家级实验教学示范中心(东北师范大学)，吉林 长春130024)

傅里叶变换光学是光学领域的一个分支，它的形成导致了光学信息处理技术的兴起. 光学信息处理以其容量大、速度快、并行性等显著优点，在二维图像信息处理和识别等方面有重要应用. 空间滤波是最基本的光学处理操作之一，其基本原理是根据具体需要制作适当的空间滤波器，并将其放在光路中输入图像的频谱平面处，通过对输入图像的频谱进行调制完成某种处理过程，如低通、高通、带通、边缘增强、相关识别等. 其理论基础是傅里叶变换，实验基础为阿贝成像原理，了解相关理论对掌握光学信息处理技术起着至关重要的作用.

1 实验原理

1.1 空间频率与频谱

任意周期结构的屏函数均可以展开为傅里叶级数. 傅里叶系数的集合反映了原函数各种频率成分所占的分量，通常称其为傅里叶谱，简称频谱. 频谱可以是连续谱，也可以是离散谱. 周期函数的频谱是离散谱，非周期函数的频谱是连续谱. 实际栅函数为准周期函数，其频谱介于连续谱与离散谱之间，而更具有离散谱的特征，称为准离散谱.

根据傅里叶分析可知，频谱面上的光场分布与物的结构密切相关，原点附近分布着物的低频信息，即傅里叶低频分量；离原点较远处，分布着物的较高的频率信息，即傅里叶高频分量[1].

1.2 阿贝成像原理

阿贝成像原理如图1所示，从频谱角度看，阿贝成像原理的基本思想是把相干光照明下的透镜成像过程分为两步：

1)物是一系列的不同空间频率信息的集合，通过物的衍射光在透镜后焦面(频谱面)上形成空间频谱，所以衍射起“分解”频谱即“分频”的作用；

2)代表不同空间频率的各光束在像平面上相干叠加而形成物体的像，因此干涉起“综合”频率即“合频”的作用[2].

图1 阿贝成像原理图

1.3 透镜的相位变化功能

设物体的复振幅透射率为t(x0,y0)，物体与透镜间的距离为d0. 使用振幅为A的单色平面波垂直照射物体，U(x0,y0)为紧靠物体后平面上复振幅分布，U1(x,y)为紧靠透镜前平面上复振幅分布，则有

U(x0,y0)=At(x0,y0),

(1)

F{U0(x,y)}=AF{t(x0,y0)}=AT(fx,fy),

F{U1(x,y)}=F{U0(x0,y0)}L(fx,fy),

(2)

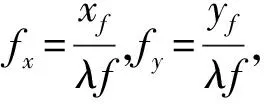
得

(3)

后焦面上的复振幅分布为

(4)

由上面的分析可见：后焦面上的复振幅分布正比于物体的傅里叶变换,变换式前的二次相位因子使物体的相位因子产生相位弯曲.

当d0=f时，即当物体位于透镜前焦面时：

(5)

1.4 空间滤波

对图像产生的复杂波前的傅里叶分析，意味着将其复杂的衍射场分解为一系列不同方向、不同振幅的平面衍射波，特定方向的平面衍射波，作为载波，携带着特定空间频率的光学信息，并将其集中于夫琅禾费衍射场的相应位置，实现了分频. 因为物信息的空间频谱展现在透镜的后焦面即傅氏面上，故若在频谱面上安置不同结构的光阑，以提取或摒弃某些频谱，从而改变了原物频谱，再合成于物的共轭像面上即为输出图像，这就完成了改造图像的信息处理. 频谱面上的光阑起选频作用，常称为空间滤波器[1].

1.5 巴比涅原理

2个互补衍射屏在衍射场中某点单独产生的复振幅之和等于光波自由传播时该点的复振幅，称为巴比涅原理. 巴比涅原理给出的3个场之间是复振幅关系，其中相位差因素也会起作用，故一衍射屏在某处的衍射强度是亮的，其互补屏在该处的衍射强度不一定是暗的.

2 实 验

2.1 探究分频、合频过程

调整好光路后，用准直的氦氖激光照明带网格的“光”字板. 先将白屏放在傅里叶透镜的后焦平面前且靠近傅里叶透镜，可看见所成像中央有一轮廓较为清晰的正立、缩小的“光”，并且“光”的周围有很多重影，发现网格已经分离[图2(a)]. 当将白屏慢慢向后焦平面移动时，中央的“光”已经被分解成更多的正立“光”，且轮廓越来越模糊，“光”也变得越来越小[图2(b)]，直至频谱面时网格已经完全分离成点阵，中央没有“光”字，只有几个光强较强的点[图2(c)]. 继续将白屏远离频谱面后方移动，白屏上的点阵逐渐消失，慢慢合成不很清晰的倒立“光”字，将屏后移，出现轮廓分明的倒立、逐渐放大了的“光”字，同时点阵也慢慢扩展复合成网格的像[图2(d)]，说明此时发生了频率的合成. 当把白屏再向后移动时，发现倒立的“光”越来越大，其上网格也越来越清晰[2][图2(e)].

(a) (b) (c)

(d) (e) 图2 探究“分频”及“合频”过程

2.2 方向滤波

2.2.1 2f成像系统

物为正交光栅，滤波器为可旋转狭缝. 用准直的氦氖激光照明光栅，后焦面上出现一系列准离散的衍射谱斑. 在后焦面上安置可以旋转的狭缝作为滤波器，以选取不同谱斑，从而可以观测到相应不同的输出图像. 如果频谱面上放置的狭缝沿纵向，则输出图像只显示横条纹；如果狭缝处于水平方位，则输出图像只显示竖条纹；如果狭缝取向倾斜，则输出图像显示为较密而且与狭缝取向垂直的斜条纹. 即改变狭缝方向，观测到像的延展方向总是与谱斑铺展方向正交，表明横向的谱斑携带的是纵向信息. 因为斜向谱斑的角间隔比水平或垂直铺展的角间隔要大，对应的基频较高，所以呈现于像平面上的斜向条纹较密，如图3～4所示.

(a)狭缝竖直 (b)狭缝水平 (c)狭缝倾斜 图3 方向滤波图(透镜为大孔径)

(a)狭缝竖直 (b)狭缝水平 (c)狭缝倾斜 图4 方向滤波图(透镜为小孔径)

2.2.2 4f成像系统

光路图如图5所示. 物为正交光栅，滤波器为可旋转狭缝. 用准直氦氖激光照明光栅，后焦面上出现一系列准离散的衍射谱斑；在后焦面上安置可旋转狭缝作为滤波器，以选取不同谱斑，从而可观测到相应不同的输出图像. 如果频谱面上放置的狭缝沿纵向，则输出图像只显示横条纹；如果狭缝处于水平方位，则输出图像只显示竖条纹；如果狭缝取向倾斜，则输出图像较为密集且与狭缝取向垂直的斜条纹.

4f系统中的“后焦面”有双重身份，对L而言是物场的频谱面；对L′而言是物平面，其频谱面即为系统的输出平面. 4f成像系统中，前后2个透镜共焦组合是必要条件，其保证了前后2次波前变换均为纯净的傅里叶变换. 透镜的前后2个焦面是1对傅里叶变换面，在4f系统中，像场是一系列不同方向平面波的干涉场，而前半部分的物场被分解为一系列不同方向的平面衍射波，即为阿贝成像原理中的“一分一合”在4f系统中的特别体现.

图5 4f成像系统原理图

对比分析2f成像系统和4f成像系统透镜孔径不同时输出图像的差异，发现透镜孔径较大时对应的输出图像包含更多细节，这是因为较大的孔径可以收集到高频信息引起的大角度的衍射光，这些衍射光到达像平面时相干叠加出较多的细节. 而孔径较小时，高频信息引起的大角度衍射无法进入镜头，频谱面上缺少了高频谱，像面上丢失了高频信息，如图6～8所示.

(a)狭缝竖直 (b)狭缝水平 (c)狭缝倾斜图6 方向滤波图(两透镜均为小孔径)

(a)狭缝竖直 (b)狭缝水平 (c)狭缝倾斜图7 方向滤波图(透镜孔径为一大一小)

(a)透镜为小孔径 (b)透镜为大孔径图8 不同孔径透镜对应的输出图像

2.3 显色滤波

实验装置如图9所示，采用白光作照明光源，频谱面上同时展现图像的时间频谱与空间频谱. 在频谱面上特定位置设置小孔滤波器，提取特定波长的空间频率成分，如图10所示.

图9 显色滤波实验装置

图10 截取不同频率滤波对应不同输出图像

调整滤波孔位置，输出图像的色彩发生改变，说明色彩是人为指定的而非天然色.

2.4 利用空间滤波技术进行图像处理

实验光路为2f成像系统，物为正交光栅，用孔径大小可调的圆孔光阑作滤波器. 实验中改变光阑孔径大小，观测输出图像的变化情况. 当逐渐缩小孔径时，观测到图像的边缘逐渐变得柔和，这是因为图像的傅里叶变换频谱中的低频分量反映图像的背景，高频分量反映图像的细节、边缘及其他尖锐跳跃，孔径缩小，使透过的高频分量减少，故边缘变得柔和，如图11所示.

(a) (b) (c) 图11 圆孔光阑孔径逐渐减小对应的滤波图像

2.5 低通滤波

2.5.1 物为带有周期性网格的“光”字

在2f成像系统中，物为带有周期性网格的“光”字，采用孔径很小的圆孔做低通滤波器，观察后焦面上的频谱分布，可以看到排成十字形的点阵. 逐步减小圆孔孔径，观察输出图像变化情况. 孔径较大时，像中存在网格结构，逐渐减小孔径，最终观测到没有网格的“光”字. 因为与网格相比，“光”字的空间频率较低，集中在光轴附近很小范围内，而孔径较小的圆孔只通过低频分量，故可将周期性网格消除，如图12所示.

(a)孔径较大 (b)孔径较小 图12 不同光阑孔径的低通滤波图像

将小圆孔移至频谱面上中央亮点以外的亮点上时，在输出平面上仍能看到无网格的“光”字，只是较暗淡. 这说明当物为“光”与网格的乘积时，其傅里叶谱是“光”的谱与网格的谱的卷积，因此每个亮点周围都是“光”的谱，再作傅里叶变换就还原成“光”字[4]，如图13所示.

(a) (b)图13 滤波孔不在频谱中心时对应的输出图像

2.5.2 物为“大”字与正交光栅组合

在2f成像系统中，将正交光栅与不透明的“大”字重叠放在物面上,选取孔径很小的圆孔作低通滤波器，观测到周期性网格被消除[5],如图14所示.

2.6 利用Matlab模拟傅里叶变换

根据傅里叶变换的性质，2个函数卷积的傅里叶变换等于傅里叶变换的乘积. 在频谱面上插入空间滤波器相当于频谱分布函数乘以空间滤波器滤波函数的复振幅透过率函数. 空间滤波的光学处理器的模拟系统简图如图15所示，通过计算机模拟仿真可以完成空间滤波实验[6].

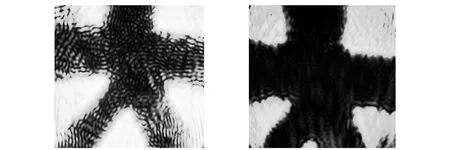
(a) (b)图14 低通滤波后的输出图像

图15 空间滤波光学处理器的模拟系统简图

2.6.1 物二维光栅的频谱

将二维光栅作为物,则可在傅里叶面上观测到如16图所示的频谱分布.

图16 二维光栅的频谱图

2.6.2 低通滤波的模拟结果

在计算机模拟中，用Photoshop软件画出带有周期性网格的“光”字图片代替物体，并保存为bmp格式. 通过Matlab编程对这幅图进行傅里叶变换得到相应的频谱分布. 这一步骤相当于实验中透镜所起的傅里叶变换作用. 图17所示为原图像及其频谱图分布.

(a)未放置滤波器

(b)放置滤波器后图17 三维频谱图

2.7 巴比涅原理的探究

在2f成像系统中，在物平面分别放置方孔和去除方孔的屏，观察二者后焦面上夫琅禾费衍射图样的区别. 在平行光照明时，其自由光场聚焦于透镜的后焦点，即轴外自由光场为零. 由巴比涅原理知，在平行光照明下，2个互补屏在后焦面上产生的夫琅禾费衍射强度分布是完全相同的，看起来是完全相同的衍射图样，不同的仅仅是像点的光强. 图18所示实验现象与理论符合[1].

(a)衍射屏为方孔 (b)衍射屏为方孔的互补屏图18 巴比涅原理实验验证图

3 结束语

空间滤波是目前应用较为广泛的光学信息处理技术，其理论依据为阿贝成像原理[7]. 本文通过实验验证了阿贝的二次成像原理，通过改变频谱结构改变了输出图像的性质，并用Matlab对相关过程进行了模拟. 其中在实现显色滤波过程中，应用自制的小孔滤波器改变频谱结构，实现了对输出图像色彩的改变，该方法操作简便且得到了明显的实验现象.

[1] 钟锡华. 现代光学基础[M]. 北京：北京大学出版社，2003.

[2] 彭小兰，王红成. 阿贝成像原理中“分频、合频”的实验演示[J]. 东莞理工学院学报，2011,18(3):38-41.

[3] 冯璐. 空间滤波实验中光路和傅里叶变换透镜孔径对实验的影响[J]. 物理与工程，2010,20(4):26-28,35.

[4] 杨述武，孙迎春，沈国土，等. 普通物理实验(三、光学部分)[M]. 5版. 北京：高等教育出版社，2016:106.

[5] 何钰. 阿贝成像原理和空间滤波实验及计算机模拟实验[J]. 物理与工程,2006，16(2)：19-23.

[6] 谢嘉宁，赵建林. 光学空间滤波过程的计算机仿真[J]. 光子学报,2002，31(7)：847-850.

[7] 张朝晖，刘国超. 阿贝成像原理和空间滤波实验[J]. 物理实验，2017,37(9):23-29.

[8] 朱昊，曹良才，何庆声. 空间滤波与体全息光存储实验[J]. 物理实验，2014,34(9)：4-8.