一种基于选择策略的差分混合蛙跳算法*
2018-01-26万小雨万建超
王 林,万小雨,万建超
(1.华中科技大学管理学院,湖北 武汉 430074;2.普天信息技术有限公司,北京 100080)
1 引言
蛙跳算法SFLA(Shuffled Frog Leaping Algorithm)是由Muzaffar和Kevin在2003年提出的,他们通过模拟青蛙种群的自然觅食过程设计出的一种群智能优化算法,并将其成功运用于地下水资源管理问题[1]。混合蛙跳算法是一种基于群体协同搜索的算法,它融合了模因算法MA(Memetic Algorithm)和微粒群算法PSO(Partical Swarm Optimization)的优点,将基因进化和种群进化有效集成在一起。
蛙跳算法的原理简单、控制参数少,具有柔性的结构框架和较强的全局信息共享能力等优点,已被成功运用于多种自然科学以及工程领域的复杂优化问题[2-4]。蛙跳算法自提出以后,众多学者对其进行理论改进和应用推广。如许方等人[5]提出一种SFLA与K均值相结合的聚类算法,抑制了早熟收敛问题;赵鹏军等人[6]在SFLA产生初始种群时采用对立学习策略提高了解的质量,并结合差分进化算法提高了种群的多样性;Roy等人[7]将遗传算法的交叉算子运用到最差青蛙个体向最好青蛙个体跳动的过程中,产生两个实验个体,提高了种群迭代效率;Zhu等人[8]让所有青蛙个体在每一次更迭中进行跳动,并利用三因素方差分析方法对SFLA的控制参数进行分析,设计出一种自适应的SFLA,实验结果说明改进后的SFLA收敛精度有所提高,但是收敛时间增长;Luo等人[9]采用多种策略产生新个体,并加入一种改进的克隆选择过程,提高了产生的新个体的质量,以及增加了种群的多样性;肖文显等人[10]将蛙跳算法的组内寻优思想嵌入和声算法中,设计了一种和声蛙跳算法,实现了两种算法的耦合动态搜索。
但是,标准蛙跳算法和现有的改进蛙跳算法的搜索时间长,存在个体之间信息交流不足、容易陷入局部最优等问题。针对这些问题,本文提出一种改进的蛙跳算法,加入实验个体选择机制,增加局部搜索中青蛙个体改进个数,并将差分进化算法的交叉算子和变异算子运用到青蛙个体跳动策略中,增加个体之间的交流。实验结果表明本文所设计的选择差分混合蛙跳算法提高了蛙跳算法的性能,该算法与其它三种改进的群智能优化算法相比,具有更好的有效性和稳定性。
2 标准蛙跳算法与缺点分析
2.1 蛙跳算法基本原理
SFLA的基本思想是:在一个水池中有一群青蛙寻找食物,每一只青蛙都有自己寻找食物的路径信息,青蛙通过不断跳动改变自己与食物之间的距离;青蛙个体按照适应度大小分为m组,每个青蛙个体携带自己的路径信息,组内进行信息交换,最优青蛙个体指导组内局部搜索方向,按式(1)~式(3)更新组内当代最差个体,重复这个过程直到满足组内搜索终止条件,具体操作如下:
Step1设置算法参数,包括组内进化代数Ne、种群总进化代数maxgen、子种群数量m、组内个体数n、种群规模popsize=m×n、最大跳动步长Smax。
Step2随机生产初始种群pop,种群中第i个个体表示为Xi=(Xi1,Xi2,Xi3,…,Xid),其中d是求解问题的维度,Xi∈[lb,ub]。计算初始种群中每个个体的适应度,并按升序排列,找出初始种群最优个体gx。
Step3将种群分为m组,每组n只青蛙。分组规则是,排序后的个体,将第1、第1+m、第1+2m、…、第popsize-m+1个个体放入第一组,将第2、第2+m、第2+2m、…、第popsize-m+2个个体放入第二组,以此类推。分组后找出组内最优个体pb和最差个体pw。
Step4组内进行局部搜索操作。按照式(1)~式(3)对pw进行更新,具体操作如下。
①采取组内最优更新策略。组内最差个体pw向组内最优个体pb方向跳动更新。通过式(1)计算跳动步长S,如果Sj<-Smax,则Sj=-Smax;如果Sj>Smax,则Sj=Smax。然后通过式(2)对pw进行更新操作,如果tempj
S=rand[0,1]×(pb-pw),S∈[-Smax,Smax]
(1)
temp=pw+S,tempj∈[lb,ub]
(2)
②采取全局最优更新策略。组内最差个体pw向全局最优个体gx方向跳动更新。通过式(3)计算跳动步长S,如果Sj<-Smax,则Sj=-Smax;如果Sj>Smax,则Sj=Smax。然后通过式(2)对pw进行更新操作,如果tempj
S=rand[0,1]×(gx-pw),S∈[-Smax,Smax]
(3)
③随机生成新个体更新策略。随机生产一个新个体替代pw,进入Step 5。
Step5对组内个体重新计算适应度,并找出更新后的pb和pw。判断是否满足组内更新终止条件,若满足,则进行Step 6,否则进行Step 4。
Step6混合洗牌,将完成局部搜索的各组个体重新混合,计算个体适应度,并按照适应度大小重新排序,找出此时的gx。判断是否满足全局搜索终止条件,若满足,则进行Step 7,否则进行Step 3。
Step7输出最佳个体gx和对应的适应度值,则为找出的最优解。
标准蛙跳算法的流程如图1所示。
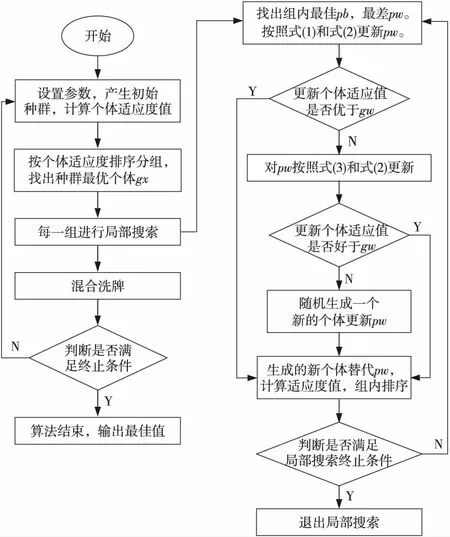
Figure 1 Flowchart of SFLA图1 标准蛙跳算法流程图
2.2 标准蛙跳算法的局限性
(1)标准SFLA和其它智能优化算法一样,没有参数设置的最优组合,而是根据不同的具体问题产生差异,并没有指导性的原则,仅能通过大量的实验得到。参数设置没有通用性,算法的稳定性不高。
(2)标准SFLA的跳动步长始终保持固定值。进化最初最大步长太小,降低收敛速度;进化进入尾声时,最大步长又太大,减弱局部搜索能力。
(3)标准SFLA在局部搜索的时候,采用三种更新策略,除了随机更新策略,另两种策略都是通过最差值向最优值方向进行跳动,更新方式过于单调,造成组内个体过分单一,种群多样性不强,容易陷入局部最优。并且在个体更新的过程中,忽略了同组内其它个体,以及种群中其它个体的信息交流,可能会错过很多优秀的基因组合。
针对以上问题,本文提出一种选择差分混合蛙跳算法,通过与差分进化算法混合,并加入选择机制和资源池操作,提高蛙跳算法的性能。
3 选择差分混合蛙跳算法(SDSFLA)
3.1 SDSFLA改进思路
SDSFLA(Selected Differential Shuffled Frog Leaping Algorithm)主要是对组内局部搜索进行改进:增加一种选择机制提高实验个体的质量;利用差分进化算法的交叉算子、变异算子,增加个体与个体之间的信息交流;引入资源池操作,增加种群多样性。SDSFLA的改进思路如下:
(1)标准蛙跳算法中,每一次组内更新只对最差个体进行一次更新操作之后,就重新排序,效率很低。在SDSFLA中,我们对组内第n-2、n-1、n个组内最差的三个个体进行更新操作,提高更新效率。
(2)组内三种更新策略产生新个体,策略①维持标准蛙跳算法更新策略不变,策略②和策略③分别引入差分进化算法的两种变异算子。三种策略中,对于跳动更新后的实验个体,引入差分进化算法中的交叉操作,产生本次更新最终的实验个体。
(3)SDSFLA的三种策略分别产生三种实验个体,选择最优的实验个体与原个体比较,这种操作有利于算法自适应地选择更好的个体进入下一代。采用多种策略产生多个实验个体,选择最优的,这种选择机制有助于增强算法的通用性。
(4)建立变异算子F和交叉算子CR的资源池,SDSFLA三种策略对个体进行更新时,随机选择F和CR的组合,增加种群多样性。本文根据Lu等人[11]提到的F、CR组合,选择了五组F、CR值,分别是[1,0.1],[1,0.9],[1,0.1],[0.8,0.2],[0.5,0.9],[0.5,0.3]。
3.2 SDSFLA局部搜索的执行流程
Step1找出组内最差的三个个体分别执行Step 2到Step 4。
Step2对要进行更新的个体local(i,:),根据以下三个策略分别进行更新操作,产生相对应的三个实验个体temp1、temp2、temp3,策略中F和CR的值是随机从[F,CR]资源池中选取出来的。
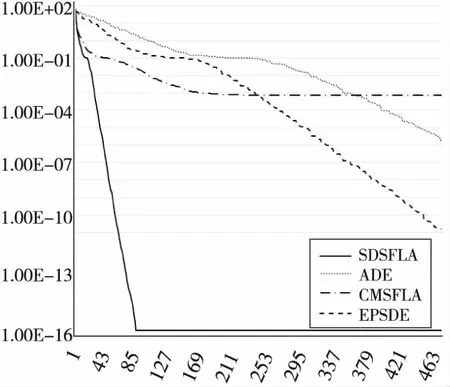
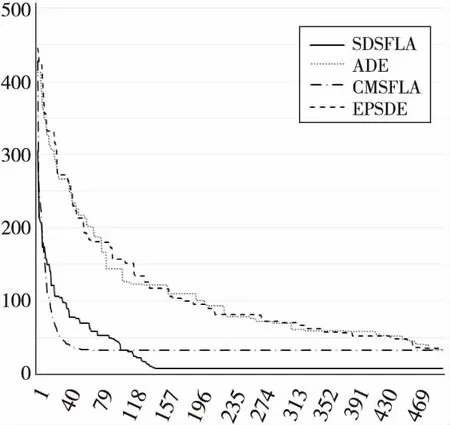
策略①:组内个体local(i,:)向组内最优个体pb方向跳动更新。组内个体local(i,:)通过式(4)计算跳动步长S,如果Sj<-Smax,则Sj=-Smax;如果Sj>Smax,则Sj=Smax。然后通过式(5)对local(i,:)进行更新操作,如果temp1j S=F×(pb-local(i,:)),S∈[-Smax,Smax] (4) temp1=(local(i,:))+S,tepm1j∈[lb,ub] (5) 策略②:组内个体local(i,:)通过式(6)计算跳动步长S,X1、X2是在组内随机选择的两个互不相同的个体,如果Sj<-Smax,则Sj=-Smax;如果Sj>Smax,则Sj=Smax。然后通过式(7)对local(i,:)进行更新操作,如果temp2j S=F×(local(X1,:)-local(X2,:)), S∈[-Smax,Smax] (6) temp2=gx+S,temp2j∈[lb,ub] (7) 策略③ :组内个体local(i,:)通过式(8)计算跳动步长S,X1、X2、X3是在组内随机选择的三个互不相同的个体,如果Sj<-Smax,则Sj=-Smax;如果Sj>Smax,则Sj=Smax。然后通过式(9)对local(i,:)进行更新操作,如果temp3j S=F×(local(X1,:)-local(X2,:)), S∈[-Smax,Smax] (8) temp3=(local(X3,:))+S,temp3j∈[lb,ub] (9) Step3将得出的三个实验个体temp1、temp2、temp3的适应度值进行比较,选择出适应度最优的个体作为最终的实验个体temp。 Step4将最终实验个体temp的适应度值与local(i,:)的适应度值进行比较,如果最终实验个体temp的适应度值优于local(i,:)的,则local(i,:)=temp,否则local(i,:)=local(i,:)。 Step5对组内个体重新计算适应度值,并且排序。判断是否满足组内更新终止条件,若满足,则退出组内局部搜索,否则转Step 1。 为检验SDSFLA的性能,本文选取了16个被广泛运用的标准测试函数[12,13],包括8个单峰函数和8个复杂多峰函数。所选取的测试函数具备不同的特征,如对称、多极值、非线性、可分离或不可分离等。16个测试函数的具体描述如表1所示。 Table 1 Test functions 16个测试函数中F3理论最优值为-1,F16理论最优值为1-n,其它函数理论最优值均为0。 本文将所提出的SDSFLA与ADE(Adaptive DE)[14]、CMSFLA(Centroid Mutated-SFLA)[15]、EPSDE(Ensemble of mutation strategies and control Parameters with the DE)[16]三种智能优化算法进行比较。其中CMSFLA和ADE算法都是2015年刚发表的改进SFLA和改进DE算法,而EPSDE算法是在其他文献中经常被用来做比较的算法之一,所以本文将提出的SDSFLA与这三种算法进行比较。 最大进化代数maxgen设置为500,种群规模为50,本文提出的SDSFLA的分组数为10,局部搜索代数为10,函数维度分别设置为30和50,每种算法对每个函数独立运行20遍,运算结果的平均值和标准差如表2和表3所示。 本文利用威尔科克森秩和检验(Wilcoxon’s rank sum test),在统计显著性为0.05的条件下,分析判断统计结果,将本文提出的SDSFLA的测试结果分别与ADE、CMSFLA、EPSDE的测试结果比较,30维和50维的比较结果如表4和表5所示(其中√、×、≈代表算法结果差于、优于、等于SDSFLA)。 图2~图5分别是较复杂的多峰函数F11、F12、F13、F14的优化过程对比图。 分析可知,针对这16个测试函数,SDSFLA明显优于其它三种算法。分析表3和表5的结果,30维函数中,SDSFLA与其他算法比较,11个优于ADE和CMSFLA,13个优于EPSDE,仅分别有1个、2个相比较差;50维函数中,SDSFLA与其他算法相比,12个优于ADE、11个优于CMSFLA,12个优于EPSDE,仅分别有1个、2个、2个结果相比较差。对于少数几个测试函数,虽然SDSFLA的运行结果稍差于其它算法,但是对于这几个测试函数,SDSFLA同样也收敛到了比较理想结果。 对于F1、F2、F4、F5、F6、F7、F9、F11这八个函数,SDSFLA的运算结果远远优于其它三种算法。分析图2~图5,在有限的搜索代数内,SDSFLA可以较快收敛到理想值。另外,通过分析标准差的结果,SDSFLA运行结果的波动性小,证明SDSFLA的稳定性较好。 Table 2 Experimental results of 30 variables Table 3 Experimental results of 50 variables Table 4 Comparison results based onWilcoxon’s rank sum test of 30 variables Table 5 Comparison results based onWilcoxon’s rank sum test of 50 variables Figure 2 Convergence results for F11图2 F11收敛结果对比图 Figure 4 Convergence results for F13图4 F13收敛结果对比图 Figure 5 Convergence results for F14图5 F14收敛结果对比图 本文将差分进化算法中产生新个体的策略与标准混合蛙跳算法结合,设计出一种SDAFLA,主要贡献如下:为解决混合蛙跳算法个体间信息交流不充分的问题,结合差分算法的变异算子和交叉算子,采用三种改进策略产生新个体,加强局部搜索过程中个体与个体之间的信息交换;实验个体选择机制,能选择更优秀的新个体,加快收敛速度;引入资源池随机选择操作,增加了种群的多样性。测试函数结果表明,SDSFLA是一种有效的智能优化算法。 本文将三种改进策略作为一个组合,并在资源池中随机选择F、CR两种控制参数的值,理论上加强了种群的多样性,提高了产生的实验个体的优秀率。未来可以利用本文提出的SDSFLA的框架,改进新个体产生策略的组合,以及资源池内控制参数的组合,加强SDSFLA解决更复杂更高维度的目标函数的能力,并用CEC2005中的测试函数进行测试,将结果与近年IEEE Transactions系列期刊论文中提出的新算法的测试结果进行比较,进一步验证SDSFLA的有效性和稳定性。 [1] Eusuff M M,Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm[J].Journal of Water Resources Planning and Management,2003,129(3):210-225. [2] Ebrahimi J,Hosseinian S H,Gharehpetian G B.Unit commitment problem solution using shuffled frog leaping algorithm[J].IEEE Transactions on Power Systems,2011,26(2):573-581. [3] Hasanien H M.Shuffled frog leaping algorithm for photovoltaic model identification[J].IEEE Transactions on Sustainable Energy,2015,6(2):509-515. [4] Lei De-ming,Guo Xiu-ping.A shuffled frog-leaping algorithm for hybrid flow shop scheduling with two agents [J].Expert Systems with Applications,2015,42(23):9333-9339. [5] Xu Fang,Zhang Gui-zhu.Clustering algorithm based on modified shuffled frog leaping algorithm andK-means[J].Computer Engineering and Applications,2013,49(1):176-180.(in Chinese) [6] Zhao Peng-jun, Shao Ze-jun.Novel improved shuffled frog leaping algorithm[J].Computer Engineering and Applications,2012,48 (8):48-50.(in Chinese) [7] Roy P,Roy P,Chakrabarti A.Modified shuffled frog leaping algorithm with genetic algorithm crossover for solving economic load dispatch problem with valve-point effect[J].Applied Soft Computing,2013,13(11):4244-4252. [8] Zhu G Y,Zhang W B.An improved shuffled frog-leaping algorithm to optimize component pick-and-place sequencing optimization problem [J].Expert Systems with Applications,2014,41(15):6818-6829. [9] Luo J,Li X,Chen M R,et al.A novel hybrid shuffled frog leaping algorithm for vehicle routing problem with time windows [J].Information Sciences,2015,316(C):266-292. [10] Xiao Wen-xian, Wang Jun-ge, Ma Xiao-qin. Harmony frog leaping algorithm and its application to complex optimization problems [J].Journal of Central China Normal University (Natural Science Edition),2016,50(2):211-215.(in Chinese) [11] Lu X, Tang K, Sendhoff B,et al.A new self-adaptation scheme for differential evolution[J].Neurocomputing,2014,146(C):2-16. [12] Wang L,Shi Y,Liu S.An improved fruit fly optimization algorithm and its application to joint replenishment problems [J].Expert Systems with Applications,2015,42(9):4310-4323. [13] Ge Yu,Wang Xue-ping,Liang Jing.Adaptive chaotic mutation shuffled frog leaping algorithms [J].Application Research of Computers,2011,28(3):945-947.(in Chinese) [14] Wang L,Zeng Y,Chen T.Back propagation neural network with adaptive differential evolution algorithm for time series forecasting [J].Expert Systems with Applications,2015,42(2):855-863. [15] Sharma S, Sharma T K,Pant M,et al.Centroid mutation embedded shuffled frog-Leaping algorithm [J].Procedia Computer Science,2015,46:127-134. [16] Mallipeddi R,Suganthan P N,Pan Q K,et al.Differential evolution algorithm with ensemble of parameters and mutation strategies[J].Applied Soft Computing,2011,11(2):1679-1696. 附中文参考文献: [5] 许方,张桂珠.一种改进的混合蛙跳和K均值结合的聚类算法[J].计算机工程与应用,2013,49(1):176-180. [6] 赵鹏军,邵泽军.一种新的改进的混合蛙跳算法[J].计算机工程与应用,2012,48(8):48-50. [10] 肖文显,王俊阁,马孝琴.和声蛙跳算法在复杂优化问题中的应用研究[J].华中师范大学学报(自然科学版),2016,50(2):211-215. [13] 葛宇,王学平,梁静.自适应混沌变异蛙跳算法[J].计算机应用研究,2011,28(3):945-947.4 SDSFLA性能测试
4.1 测试函数介绍

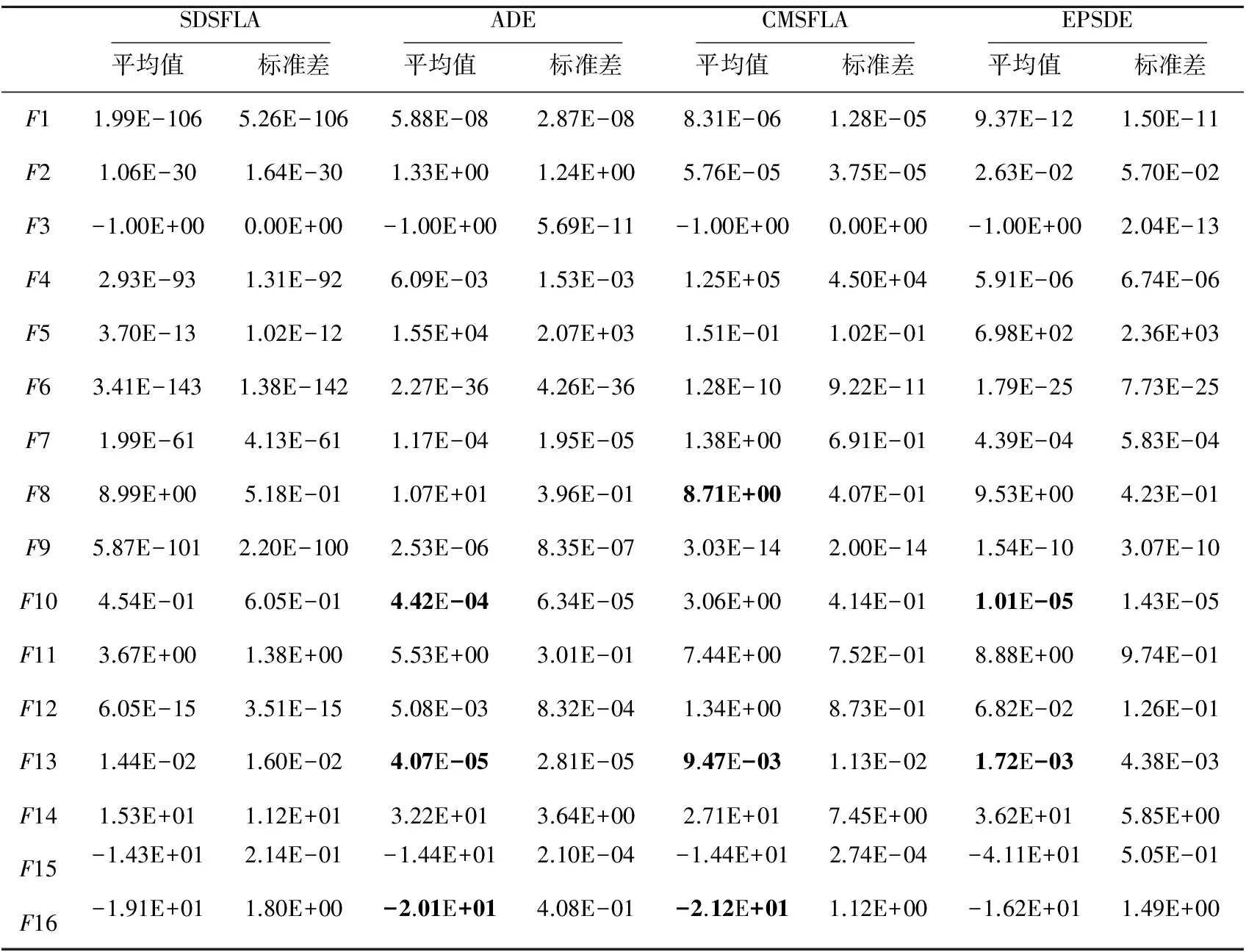
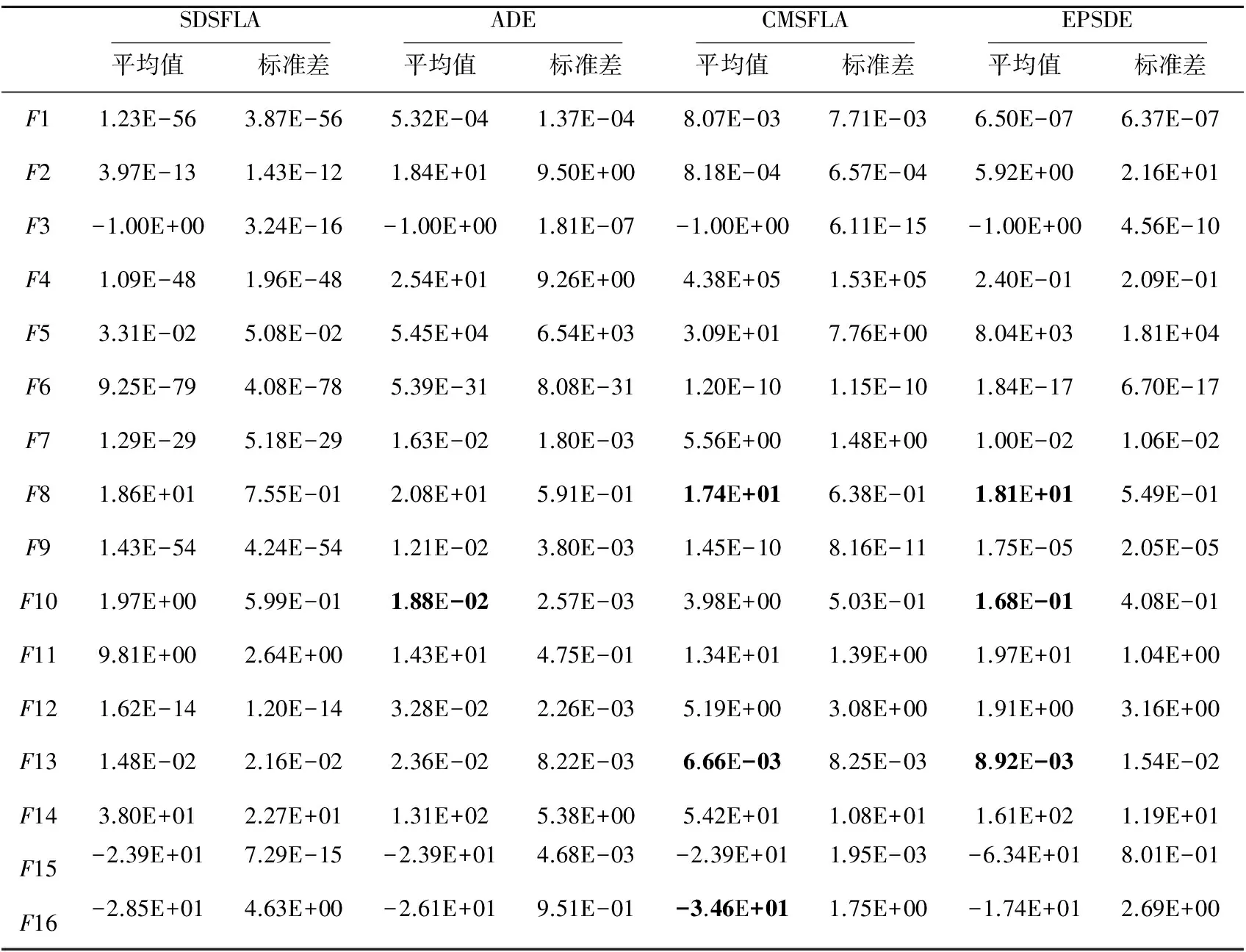
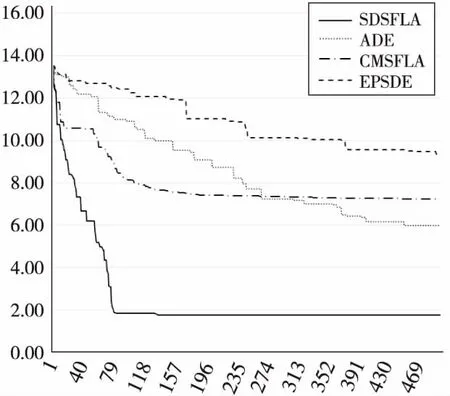
4.2 测试结果


5 结束语
