PFPonCanTree：一种基于MapReduce的并行频繁模式增量挖掘算法*

肖 文，胡 娟，周晓峰

(河海大学文天学院,安徽 马鞍山 243000)

1 引言

频繁模式挖掘是最重要的数据挖掘任务之一，也是很多数据挖掘任务的基础性任务，自从它被提出以来[1]，受到了越来越多研究者的关注。频繁模式挖掘的目的是发现事务数据中频繁出现的模式，从而发现事物项之间存在的隐含关联。已经提出的频繁模式挖掘算法大致可以分为三类：第一类是通过迭代产生候选频繁模式并对它们分别进行计数，将模式的支持度与最小支持度比较来获得频繁模式，典型的算法是Apriori[2]及其一系列的改进算法；第二类是不产生候选模式，通过将数据集压缩成一种特殊的数据结构(一般为树结构)，在特定结构上进行遍历来直接产生频繁模式，典型的算法有FP-Growth[3]、LP-Tree[4]、FIUT[5]、IFP[6]、FPL/TPL[7]等；第三类是将水平格式的数据集转换成垂直格式，通过交运算来得到频繁模式，典型的算法有Eclat等。

上述列举的频繁模式挖掘算法都是基于被挖掘的数据集是“静态的、不变的”这样一个基本的假设，以“批处理”的方式对整个数据集进行挖掘。但是，在现实世界中，数据集却是始终变化的，不断有新的事务数据插入到数据集中，导致产生新的频繁模式，或是使原来频繁的模式不再频繁。对于更新后的新数据集，如果仍以批处理的方式对其进行重新挖掘，其效率十分低下。在不断变化的数据集中进行频繁模式挖掘，需要充分利用前一阶段的挖掘结果，以“增量挖掘”的方式进行，提高挖掘效率。

为实现频繁模式的增量挖掘，研究者已经提出了一些解决的方法，如基于Apriori算法的增量挖掘算法FUP(Fast Update)[8]、FUP2(Fast Update 2)[9]、UWEP(UpdateWithEarly Pruning)[10]、GSP(Generalized Sequential Patterns)[11]、Pre-Large[12]等，基于树结构的AFPIM(Adjusting Frequent Pattern Tree Structures)[13]、FELINE(基于CATS-Tree(Compressed & Arraged Transcation Sequence Tree)结构)[14]、CanTree(Canonical-order Tree)[15]、BIT(BatchIncremental Tree)[16]算法等。基于Apriori的增量挖掘算法虽然充分利用了对原始数据库挖掘过程中产生的所有计数和挖掘结果，但仍需要迭代产生候选模式并进行多次计数，不适合大量数据集的增量挖掘任务。基于树的增量挖掘方法虽然在一定程度上解决了增量挖掘的问题，但需要将所有数据以树的形式存储在内存中，对于存储空间需求量很大。频繁模式挖掘是一种计算、存储密集型计算任务，在当前大数据时代，传统增量挖掘算法无法满足海量数据挖掘的需要，主要体现在：在单一计算机上无法存储所需要挖掘的所有数据及挖掘过程中产生的中间结果，所需要的内存远远超过单一机器的存储量，计算时间太长无法忍受等。需要开发分布式、并行的增量关联规则挖掘算法解决大数据中频繁模式增量挖掘的问题。

MapReduce是一种由Google提出的易用且功能强大的并行编程模型，具有使用简单、自动容错、负载均衡、伸缩性好等优点，已经有了很多将传统频繁模式挖掘算法向MapReduce模型进行迁移的研究[17 - 36]，很大程度上解决了大数据中频繁模式挖掘的问题。在MapReduce计算模型中，一个计算任务被分为Map和Reduce两个方法。Map方法在多个结点上运行，处理一个或多个本地的数据分片；Reduce方法处理Map方法输出的中间结果，也可以多个Reduce方法并行执行；所有Reduce方法的输出合并后得到最后的结果。MapReduce计算模型流程图如图1所示。

Figure 1 MapReduce parallel programming model图1 MapReduce并行编程模型

Hadoop[37]是MapReduce的一个开源实现，同时提供了一个分布式文件系统HDFS(Hadoop Distribtued File System)。HDFS是一个用来存储超大文件的文件系统，可以自动地对超大文件进行分片及负载均衡。HDFS将分片存储在不同的结点上，同时在存储分片的结点上执行MapReduce计算任务，通过数据本地化、减少I/O来提高运行效率。一个Hadoop集群可以运行在普通的商用计算机上，包括一个Master结点和多个Slave结点。

本文主要贡献为：

(1)提出了PFPonCanTree算法，将传统频繁模式增量挖掘算法CanTree向MapReduce计算模型进行了迁移，实现了并行、分布式的频繁模式增量挖掘。

(2)设计了并行计算中各结点的负载均衡策略，使得每个结点计算量相对平衡，提高整个算法运行效率。

(3)对算法的执行效率进行了定量分析，并通过实验验证了分析结果。

本文的组织如下：第2节对有关工作进行了综述；第3节提出基于MapReduce计算模型的并行频繁模式增量挖掘算法PFPonCanTree，并进行了效率分析；第4节介绍了实验环境和方案，并对实验结果进行了分析；第5节对全文进行了总结，并对下一步工作进行了展望。

2 问题定义与相关研究

2.1 问题描述与符号定义

设I={i1,i2,…,in}为项的集合；P是一个模式，P={i1,i2,…,in}⊆I，包含k个项的模式称为k-模式；一个事务T的定义为T=(tid,X)，其中tid为事务标识，X为一个模式；一个事务数据库D是多个T的集合。

模式Y在事务数据库D中的支持度为D中包含模式Y事务的比例。定义为：

如果一个模式被称为是频繁的，则其支持度不小于用户给定的一个阈值(σ),这个阈值也称为最小支持度(min_sup)。频繁模式具有单调特性，即：如果一个模式是频繁的，则其所有子模式都是频繁的。相应地，如果一个模式不是频繁的，则其所有的超模式都是不频繁的。

对于频繁模式的增量挖掘问题，定义如表1所示的符号。

Table 1 Symbol description

增量挖掘，即是要充分利用对D的已有挖掘结果，对T进行分析挖掘，提高对U进行挖掘的效率。

2.2 FELINE(CATS-Tree)

Cheung等[14]于2003年设计了一种特殊的树结构CATS-Tree用于实现增量模式挖掘。构造D的CATS-Tree只需要扫描数据集一次，依次将每一条事务T中的所有项插入树中。在插入事务T时，从root节点开始，将T中的项和当前节点的每一个孩子比较，如果相同就合并，将当前节点改变为合并的节点，并比较下一项；如果没有相同的项，则将T中的项做为一条新的路径插入CATS-Tree中。如果树中一个节点的支持度比它的祖先高，则将它与其祖先交换，保证每一个节点的支持度都不大于它的祖先。构造CATS-Tree完成后，可以使用传统的FP-Growth算法在CATS-Tree上进行频繁模式挖掘。

虽然CATS-Tree具有构造简单、保存了D中的所有信息、插入新事务方便等特点，但它存在两个明显的缺点：一是CATS-Tree的构造过程中存在搜索公共项，随着局部支持度的变化交换和合并节点等操作，增加了额外的系统开销；二是根据CATS-Tree的特点，在使用FP-Grwoth算法进行挖掘阶段时从向上和向下两个方向遍历才能得到一个项的条件模式基，会造成大量的系统负载。

2.3 CanTree

为了克服CATS-Tree的缺点，Leung等[15]在2007年提出了CanTree。CanTree与CATS-Tree相同，也是将事务中的所有项都插入到树中，但在插入事务之前，会将事务中的项按照一个预先定义的顺序(可以为字典或字母表顺序，也可以使用项的某一种属性)进行排列，使得树中的节点顺序与局部支持度无关，不需要进行额外的交换操作，且大大减少了搜索公共项的系统消耗，并且获得项的条件模式基只需要向上的顺序进行遍历，减小了系统负载。对于新插入的事务集，可使用上述方法很容易地将新事务插入树中，实现增量挖掘。构造完CanTree后，也可以使用类似FP-Growth算法进行挖掘。Hoseini等在2015年提出了一种在CanTree上进行挖掘的新方法[38]，方法与FP-Growth类似，只不过在创建项的条件模式基时只选择路径上频繁的项，减少了构造的条件树的节点数。

从CanTree的特点来分析，它保存了D中的所有信息，插入新事务也非常方便，十分适合用于增量频繁模式挖掘；构造CanTree只需要扫描D一次，且构造过程中没有交换节点的额外操作，搜索公共项的效率也十分高，构造CanTree效率高；对Can-Tree挖掘的方法与FP-Growth类似，可以对所有项进行分组，将不同分组及组相关事务分发给不同的结点并行执行，可以很方便地将CanTree的构造和挖掘移植到MapReduce计算模型及其开源实现平台Hadoop上，通过并行化实现在大数据集中的频繁模式增量挖掘。

2.4 PFP

Li等[24]在2010年提出了并行FP-Growth算法PFP，实现了将FP-Growth算法向MapReduce计算模型上的移植。PFP算法使用了三个MapReduce任务完成整个并行挖掘工作。使用HDFS将大数据进行自动分片，在第一个任务中对所有项进行并行计数，得到所有频繁项的集合(FList)。将FList进行分组后得到组列表(GList)。第二个任务的主要目的是得到“组相关事务集”,即包含该组中项的所有事务的集合。每个Mapper启动时，加载GList以及本结点所存储的数据分片，输出每一组相关联的事务T，在Reduce阶段进行合并，得到每一组相关联的所有事务T的集合。第三个任务的Map函数对组及组相关联事务使用传统的FP-Growth算法进行挖掘，Reduce函数将所有局部频繁项集合并得到全局频繁项集。PFP算法执行流程见图2。

Figure 2 Flow chart of PFP algorithm图2 PFP算法流程图

PFP算法最显著的优点是：多个组及组相关事务之间是相互独立的，不同的组可以在不同的计算结点上独立运算，结点之间不需要相互等待和通信，最合适分布式运算。但是，缺点也很明显：频繁项的分组没有考虑负载均衡，可能会造成有的计算结点计算任务很重，而有的结点计算任务很轻；与一个项相关联的事务可能非常多，无法在一个计算结点上构造FP-Tree进行频繁项集挖掘；将项和相关事务分发到单独结点时，会产生很大的通信量。

3 PFPonCanTree算法

3.1 PFPonCanTree算法概述

给定一个原始数据集D及一批新的事务集T，PFPonCanTree算法分两个阶段分别对它们进行处理，共需要4个MapReduce任务完成并行挖掘任务。算法简要描述如下：

第一阶段：对D进行并行挖掘。

Setp1D-分片。将数据集D分割为i个连续部分，并分别存储在p个计算结点上，每一个部分称为一个数据分片。这个过程可以通过将数据集D存储在Hadoop的分布式文件系统HDFS上，由HDFS自动完成。

Setp2D-并行计数。使用一个MapReduce任务来统计D中所有的项及其支持度。每个Mapper输入一个或多个本结点上存储的数据分片，分片中的所有项以〈item,1〉的键值对形式发送给Reducer，Reducer汇总相同项的计数，得到D中所有项的集合I及其支持度。

Setp3I-平衡分组。将I中的所有项根据支持度降序排列后，将I分成Q组。设Ii是I中的第i个项，Qi为Ii的组号，使用负载均衡的分组策略：

很显然，支持度越高的项其相关联的事务也越多。将项根据其支持度进行均衡分组，使得每一个组的相关事务集的数量相对均衡，有利于在分布式构造CanTree及挖掘时实现负载均衡。平衡分组可以在一个计算结点上完成，保存每个项及其组号的对应关系。

Setp4D-并行挖掘。这个步骤是第一阶段的关键步骤。这一阶段使用一个MapReduce任务来完成。Map阶段根据项的分组情况，生成本地数据分片中的组相关事务，根据组号发送给对应计算节点。Reduce阶段构造组相关事务的CanTree，并在CanTree上使用传统的FP-Growth算法进行挖掘。Reduce阶段构造的组相关CanTree及HeaderTable在挖掘完毕后存储在计算结点中，作为下一步增量挖掘的基础。有关实验表明，由于树的构造是一种递归计算任务，基于树的频繁模式挖掘算法构造树的时间要远远大于在树上进行遍历挖掘的时间，因此在增量挖掘阶段复用已经构造的树可以大大减少挖掘的时间，免去重新构造树的系统开销。

Setp5D-聚集。如有需要，将Step 4中每个Reduce产生的频繁模式进行汇总，输出数据集D的频繁模式。

至此，第一阶段对原始数据集D的并行频繁模式挖掘就结束了。可以看到，这一阶段的执行与PFP算法十分相似，区别在于三点：一是对项的分组考虑到了负载均衡的要求，依据项的支持度进行分组；二是在构造组相关事务集的树时，构造的是CanTree而不是FP-Tree；三是挖掘结束后，CanTree和对应的HeaderTable并不丢弃，而是做为下一阶段增量挖掘的基础。

第二阶段：对T进行并行增量挖掘。

Setp6T-分片。将新事务集T分割为i个连续部分，将数据分片存储在p个计算节点上。这个过程同样可以由HDFS自动完成。

Setp7T-并行计数。使用一个MapReduce任务来统计T中所有的项及其支持度。每个Mapper输入一个或多个本节点上存储的T的数据分片，分片中的项以〈item,1〉的键值对形式发送给Reducer，Reducer汇总相同项的计数，得到T中所有项的集合I′及其支持度。

Setp9U-并行挖掘：该步骤是第二阶段的关键步骤。这一阶段使用一个MapReduce任务来完成。Map阶段根据U-项分组信息和计算结点的对应关系，将T的组相关事务发送给相应的计算结点。Reduce阶段将新的事务更新到原CanTree上，更新完毕后使用FP-Growth算法进行挖掘。传统的FP-Growth算法从HeaderTable的最后一项(即支持度最低的项)开始构造条件模式基础，由于CanTree中存储了所有项的信息，有些项可能并不频繁，因此在挖掘过程中可以稍加改进，只需要考虑支持度大于min_sup的项即可。

Setp10U-聚集：将Step 9中每个Reduce产生的频繁模式进行汇总，作为最终的结果。

两阶段完成后，U可以被看做是下一次增量挖掘的D。当有新的事务集T′到来时，重复算法的第二阶段即可实现对新加入的T′进行挖掘，得到整个更新数据集U′的频繁模式。两阶段流程图如图3所示。

Figure 3 Flow chart of PFPonCanTree algorithm图3 PFPonCanTree算法流程图

3.2 PFPonCanTree效率分析

将提出的算法与批处理并行算法PFP进行比较分析。设有数据集为D，新事务集为T，更新后的数据集为U，|D|=d，|T|=t，|U|=u，u=d+t；每条事务包含项的平均数为n，D被分为i个分片存储在p个计算结点上，T被分为j个分片存储在p个节结上，平均频繁项的比例为s。PFP不是增量挖掘算法，当T加入D更新得到U后，只能对U重新进行并行挖掘，其执行时间主要由6部分组成：

tPFP=t分片+t并行计数+t项分组+t分布式挖掘+t数据传输

而若使用PFPonCanTree算法，对T可以进行增量挖掘，增量挖掘除第一次挖掘外，其余只执行算法的第二阶段，则增量挖掘的执行时间也主要由6部分组成：

数据分片由HDFS自动完成，项分组都是简单操作，因此两个算法这两部分差异较小，可以忽略其差异。两个算法的执行时间主要取决于项并行计数、分布式挖掘两个环节及数据传输的时间。由于对数据的操作时间要远远低于数据传输的时间，特别是在分布式计算的条件下，数据传输的时间对算法效率更有显著的影响。在相同集群条件下，数据传输时间的差异即是需要传输数据量的差异。

(1)对并行计数环节来说，两个算法都需要一个MapReduce任务，使用相同的方式进行。两者的差别在于需要处理的事务数及需要在Map和Reduce之间传输的项的数量。很明显，PFP算法需要处理u个事务，而PFPonCanTree算法需要处理t个事务；u个事务会产生u*n个需要传输的项，而PFPonCanTree算法为t*n个。这一阶段的加速比为：

(2)对分布式挖掘环节来说，两个算法都需要一个MapReduce任务，使用类似的方式进行。该环节主要包含三个阶段：生成组相关事务、构造树结构、使用FP-Growth算法进行挖掘。由于挖掘使用的方法一致(都是使用FP-Growth算法)，挖掘的对象一致(都是U的CanTree)，因此两个算法效率的差别主要在第一和第二阶段。PFP算法最多需要传输|I|*u条事务，而PFPonCanTree最多需要传输|I′|*t条事务。

在构造树结构阶段，PFP需要重新构造FP-Tree，而PFPonTree算法只需要将新的事务更新到原有的CanTree上去。由于CanTree中存储事务所有的项而非只有频繁的项，因此CanTree比FP-Tree需要更多的存储空间。这一阶段的加速比为：

S分布式挖掘=|I|*u/(|I′|*t)≈(u/t)2

从上述分析可以看到，伴随着数据集的不断增长，u和t的差值会越来越大，PFPonCanTree会越来越体现出更好的效率，由于增量挖掘的特性，提出的算法只需要处理新增的T即可，比重新开始挖掘U数据集有明显的性能优势。

4 实验方案结果分析

使用基于MapReduce计算模型的开源系统Hadoop 1.2.1做为平台搭建实验集群，具体方案如下：使用1台计算机做为Master结点,CPU为 i7-4790 3.60 GHz 8核，内存8 GB，操作系统为Red Hat Enterprise Linux Server 6.6，Java平台为Java 1.6；使用6台计算机做为Slave结点，CPU为 i3-4150 3.50 GHz 4核，内存4 GB，操作系统为Red Hat Enterprise Linux Server 6.6，Java平台为Java 1.6。集群计算机之间使用百兆以太网相互连接；使用Java语言编写PFP和PFPonCanTree算法，将两个算法效率进行对比。所使用的实验数据集具体属性如表2所示。

Table 2 Specific attributes of experimental data sets

4.1 负载均衡实验

算法的负载均衡主要取决于分布式挖掘阶段各计算结点的处理数据量。使用来自Frequent Itemset Mining Dataset Repository[39]中的Mushroom数据集做为实验数据集，使用算法Step 3负载均衡项分组策略，将所有项依次分为6、12、18组，每一组的组独立事务数量如图4～图6所示。

Figure 4 Number of related transactions in each group when all items are divided into 6 groups图4 将所有项分为6组时每个组相关事务集数量

Figure 5 Number of related transactions in each group when all items are divided into 12 groups图5 将所有项分为12组时每个组相关事务集数量

Figure 6 Number of related transactions in each group when all items are divided into 18 groups图6 将所有项分为18组时每个组相关事务集数量

从图4～图6可以看出，本文提出的项分组策略取得了很好的效果，使得在分布式挖掘阶段每一个计算结点所处理的数据量十分接近，实现了较好的负载均衡。另外还可以看出，随着分组数的不断增加，每一组所包含的事务数随之减少，因此可以通过尽可能地扩大分组数，使分布式挖掘阶段启动更多的Reduce方法，提高并行化程度。设集群中有p个计算结点，每个结点能够运行的最大Reduce方法数为r，则最大分组数Q可以由以下公式计算得到：

Q=p*r

这样可以充分利用每一个计算结点的计算能力，同时也可以使Map方法的输出发送到更多的结点，有利于实现网络通信的负载均衡。

4.2 算法执行效率实验

设计三组实验，使用PFP算法对更新数据集进行批处理挖掘，使用PFPonCanTree算法对增量数据进行增量挖掘，最低支持度为0.025%，三组实验数据如表3所示。

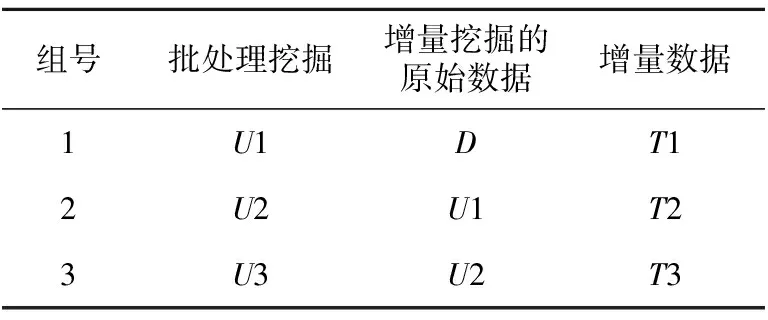
Table 3 Three groups of experimental data

三组实验的执行时间如图7所示。

Figure 7 Run time of three groups of experimental data图7 三组实验数据运行时间

从实验结果可以发现：

(1)增量挖掘算法实现了较好的效率提高，其执行时间减少主要是因为两点：一是增量挖掘阶段不用重新生成D的组相关事务，大大减少了分布式挖掘阶段Map方法的输出和网络上的I/O传输数据量；二是构造树是一种递归计算，需要大量的计算资源。增量挖掘阶段更新原CanTree要远远快于重新构造更新数据集U的CanTree，提高了效率。

(2)提出的PFPonCanTree算法具有较好的线性加速度，适合于进行进一步扩展。

5 结束语

本文提出了一种基于MapReduce计算模型的并行频繁模式增量挖掘算法PFPonCanTree。算法基于传统的增量挖掘CanTree数据结构及并行频繁模式挖掘算法PFP的基本思想，使用均衡负载对项进行了平衡分组，减少了增量挖掘阶段I/O数据量及构造CanTree的计算量。实验结果表明，提出的算法在负载均衡及执行效率上都有较好的表现。下一步的工作可以进一步优化Hadoop运行环境，提高分布式挖掘阶段Map方法的并行度，进一步提高算法的执行效率。

[1] Agrawal R, Imielinski T, Swami A N. Mining association rules between sets of items in large databases[C]∥Proc of the ACMSIGMOD Conference on Management of Data,1993:207-216.

[2] Agrawal R,Srikant R.Fast algorithm for mining association rules in large databases[C]∥Proc of the 20th International Conference on Very Large Data Bases,1994:487-499.

[3] Han Jia-wei,Pei Jian,Yin Yi-wen,et al.Mining frequent patterns without candidate generation: A frequent-pattern treeapproach[J].Data Mining and Knowledge Discovery,2004,8(1):53-87.

[4] Pyuna G, Yun U, Ryu K H.Efficient frequent pattern mining based on linear prefix tree[J].Knowledge-Based Systems,2014,55:125-139.

[5] Tsay Y J, Hsu T J, Yu J R. FIUT:A new method for mining frequent itemsets[J].Information Sciences,2009,179(11):1724-1737.

[6] Lin Ke-chung,Liao I-en,Chen Zhi-sheng.An improved frequent pattern growth method for mining association rules[J].Expert Systems with Applications,2011,38(5):5154-5161.

[7] Tseng Fan-chen. An adaptive approach to mining frequent itemsets efficiently[J].Expert Systems with Applications,2012,39(39):13166-13172.

[8] Cheung D W,Han J,Ng V T,et al.Maintenance of discovered association rules in large databases: An incremental updating approach[C]∥Proc of the 20th IEEE International Conference on Data Engineering,1996:106-114.

[9] Cheung D W, Lee S D,Kao B.A general incremental technique for maintaining discovered association rules[C]∥Proc of International Conference on Databases Systems for Advanced Applications,1997:185-194.

[10] Ayan N F,Tansel A U, Arkun E. An efficient algorithm to update large itemsets with early pruning[C]∥Proc of Acm-sigkdd International Conference on Knowledge Discovery & Data Mining,1999:287-291.

[11] Srikant R,Agrawal R.Mining sequential patterns: Generalizations and performance improvements[C]∥Proc of the 5th Conference on Extending Database Technology,1996:3-17.

[12] Hong T P,Wang C Y,Tao Y H.A new incremental data mining algorithm using pre-large itemsets[J].Intelligent Data Analysis,2001,5(2):111-129.

[13] Koh J L,Shieh S F.An efficient approach for maintaining association rules based on adjusting FP-tree structures[M]∥Database Systems for Advanced Applications.Berlin:Springer Berlin Heidelberg,2004:417-424.

[14] Cheung W, Zaïane O R. Incremental mining of frequent-patterns without candidate gneration or support constraint[C]∥Proc of the 2003 International Database Engineering and Applications Symposium,2003:111-116.

[15] Leung K S，Khan Q I，Hoque T.Cantree: A tree structure for efficient incremental mining of frequent patterns[C]∥Proc of the 5th IEEE International Conference on Data Mining,2005:8.

[16] Totad S G, Geeta R B G, Reddy P P.Batchprocessing for incremental fp-tree construction[J].International Journal of Computer Applications,2010,5(5):28-32.

[17] Li N,Zeng L,He Q,et al.Parallel implementation of apriori algorithm based on mapreduce[C]∥Proc of Acis International Conference on Software Engineering,Artificial Intelligence,Networking and Parallel & Distributed Computing,2012:236-241.

[18] Huang Li-qin,Liu Yan-huang.Research on improved parallel Apriori with MapReduce[J].Journal of Fuzhou University(Natural Science Edition),2011,39(5):680-685.(in Chinese)

[19] Sun Zhao-xu,Xie Xiao-lan,Zhou Guo-qing,et al.Implemention of Apriori based on Hadoop[J].Journal of Guilin University of Technology,2014,34(3):584-588.(in Chinese)

[20] Zhou X,Huang Y.An improved parallel association rules algorithm based on mapreduce framework for big data[C]∥Proc of the 2014 10th International Conference on Natural Computation,2014:284-288.

[21] Zhou Guo-jun,Gong Yu-tong.Frequent item sets mining algorithm based on MapReduce and matrix[J].Microelectronics & Computer,2016,33(5):119-123.(in Chinese)

[22] Li L, Zhang M. The strategy of mining association rule based on cloud computing[C]∥Proc of International Conference on Business Computing and Global Informatization,2011:475-478.

[23] Yu R M,Lee M G,Huang Y S,et al.An efficient frequent patterns mining algorithm based on mapreduce framework[C]∥Proc of International Conference on Software Intelligence Technologies and Appliations,2014:1-5.

[24] Mao W,Guo W. An improved association rules mining algorithm based on power set and hadoop[C]∥Proc of International Conference on Information Science and Cloud Computing Companion,2013:236-241.

[25] Liu S H,Liu S J,Chen S X,et al.IOMRA—A high efficiency frequent itemset mining algorithm based on the MapReduce computation model[C]∥Proc of IEEE International Conference on Computational Science and Engineering,2014:1290-1295.

[26] Yahya O,Hegazy O,Ezat E.An efficient implementation of Apriori algorithm based on hadoop-mapreduce model[J].International Journal of Reviews in Computing,2012,12:59-63.

[27] Farzanyar Z,Cercone N.Efficient mining of frequent itemsets in social network data based on mapreduce framework[C]∥Proc of 2013 International Conference on Advances in Social Networks Analysis and Mining (ASONAM),2013:1183-1188.

[28] Farzanyar Z, Cercone N. Accelerating frequent itemsets mining on the cloud: A mapreduce-based approach[C]∥Proc of IEEE International Conference on Data Mining Workshops,2013:592-598.

[29] Huang D,Song Y,Routray R,et al.Smartcache: An optimized MapReduce implementation of frequent itemset mining[C]∥ Proc of IEEE International Conference on Cloud Engineering,2015:16-25.

[30] Viana S. Matrix apriori: Speeding up the search for frequent patterns[C]∥Proc of Iasted International Conference on Databases and Applications,2006:75-82.

[31] Li H,Wang Y,Zhang D,et al.Pfp:Parallel fp-growth for query recommendation[C]∥Proc of ACM Conference on Recommender Systems,2008:107-114.

[32] Yang Yong, Wang Wei.A parallel FP-growth algorithm based on Mapreduce[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2013,25(5):651-657.(in Chinese)

[33] Zhou L,Zhong Z,Chang J,et al.Balanced parallel fp-growth with mapreduce[C]∥Proc of 2010 IEEE Youth Conference on Information Computing and Telecommunications (YC-ICT),2010:243-246.

[34] Yong W,Zhe Z,Fang W.A parallel algorithm of association rules based on cloud computing[C]∥Proc of International ICST Conference on Communications and Networking in China,2013:415-419.

[35] Chen Xing-shu, Zhang Shuai,Tong Hao,et al.FP-growth algorithm based on Boolean matrix and MapReduce[J].Journal of South China University of Technology (Natural Science Edition),2014,42(1):135-141.(in Chinese)

[36] Xun Y,Zhang J,Qin X.Fidoop: Parallel mining of frequent itemsets using MapReduce[J].IEEE Transactions on Systems Man & Cybernetics Systems,2015,46(3):1.

[37] Welcome to ApacheHadoop![EB/OL].[2017-01-10].http:∥hadoop.apache.org/.

[38] Hoseini M S, Shahraki M N,Neysiani B S.A new algorithm for mining frequent patterns in CAN tree[C]∥Proc of International Conference on Knowledge-Based Engineering and Innovation,2015.

[39] Frequent itemset mining dataset repository[EB/OL].[2016-12-01].http:∥fimi.ua.ac.be/data/.

附中文参考文献：

[18] 黄立勤,柳燕煌.基于MapReduce并行的Apriori算法改进研究[J].福州大学学报(自然科学版),2011,39(5):680-685.

[19] 孙赵旭,谢晓兰,周国清,等.基于Hadoop的Apriori算法与实现[J].桂林理工大学学报,2014,34(3):584-588.

[21] 周国军,龚榆桐.基于MapReduce和矩阵的频繁项集挖掘算法[J].微电子学与计算机,2016,33(5):119-123.

[32] 杨勇,王伟.一种基于MapReduce的并行FP-growth算法[J].重庆邮电大学学报(自然科学版),2013,25(5):651-657.

[35] 陈兴蜀,张帅,童浩,等.基于布尔矩阵和MapReduce的FP-Growth算法[J].华南理工大学学报(自然科学版),2014,42(1):135-141.