容错处理器阵列的多逻辑列并行重构算法*
2018-01-26章子凯武继刚姜文超刘竹松
章子凯,武继刚,姜文超,刘竹松
(广东工业大学计算机学院,广东 广州 510006)
1 引言
随着纳米科技的不断进步,超大规模集成电路VLSI(Very Large Scale Integration)的集成技术和制造工艺发展日趋成熟,单一芯片上可以集成的处理器单元也越来越多。这些芯片可以并行高速处理大量的数据信息,多核、众核高性能计算机的计算能力得到了极大增强。然而,在集成密度呈指数倍增长的趋势下,大规模集成电路制造和使用过程中处理器单元出现故障的概率也随之增大,严重影响了电路的可靠性。所以,为片上网络设计快速高效的容错系统,是一个十分有意义的研究课题。
最常用的容错技术为冗余重构方法(Redundancy Approach)和降阶重构方法(Degradable Approach)。在冗余重构方法[1 - 5]中,原有处理器阵列上额外附加了预先固定数目的冗余处理器单元,当处理器阵列中某些常规单元出现故障时,冗余单元将会替代故障单元。这种方法重构出的目标阵列是固定的。虽然冗余方法比较容易实现,但是它通常需要足够数量的备用处理器单元。一旦冗余处理器单元替代失败,系统将会失效。在降阶重构方法[6 - 8]中,阵列中不附加额外的处理器单元。当阵列中某些单元出现故障时,使用尽可能多的无故障单元来重构出一个目标阵列,最大限度地提高无故障处理器单元的利用率。在实际应用中可以根据需求来灵活调整目标阵列的大小,但重构后所得阵列规模通常小于初始物理阵列。
文献[9]利用启发式算法以及文献[10]利用遗传算法,将规模较小的物理阵列重构出一个最大的目标阵列。文献[11]提出了基于启发式策略和动态规划思想的新技术,通过降低目标阵列中长连接的数目来减少通信链路的长度,从而在保持系统性能的前提下降低了功率的损耗。文献[12]提出了一种新的技术来加速可降阶的处理器阵列的重构过程。文献[13]研究了在含有开关故障的情况下处理器阵列上的选路策略。
此外,文献[14]将二维阵列上的重构问题推广到三维阵列上,提出了一种三维处理器阵列上的贪心列选路算法。文献[15]提出了三维的处理器阵列上的不回溯的重构算法,该方法在不丢失逻辑列的情况下,通过消减回溯的操作加速重构过程。
但是,这些重构技术大多数都是讨论串行重构算法,对于并行重构算法的研究尚不多见。文献[16]提出了基于多线程技术的并行重构算法,但是后继线程必须在前一个线程选路深度达到一定条件时才能开始。文献[17]提出了横向划分的基于分治策略的并行构造单一逻辑列的算法,使得重构速度有了很大的提升,加速比的提升尤为显著。因为单条逻辑列的重构生成可能波及到物理阵列上的很大区域(类似于数据的强相关性)。所以逻辑列的并行生成以及逻辑列的归并过程,会使得相关性很强的数据被重复读取和擦除。事实上,在重构过程中由于没有办法判断在物理阵列上能够波及的具体范围,往往需要把整个物理阵列都读取进来。这种没有细致考虑处理器之间依赖性的划分方式,使得内存读取数据冗余很多,总线通信量很大甚至会出现拥堵,运算过程不够连贯,数据利用率较低。文献[18] 采用硬件描述语言 VHDL(Very-High Speed Integrate Circuit Hardware Description Language)设计重构了文献[16]中的算法,通过引脚协调相邻选路过程之间的矛盾,使得该算法能够多列同时向下选路,提高了重构效率。但是,该算法重构出的阵列不能保证是最大的目标阵列,而且算法扩展到大规模处理器阵列时,性能不佳。
本文提出了基于横向分块划分的并行分治重构策略,在行穿越和列选路约束条件下,实现了最大的目标子阵列的重构,最大限度地保证了大规模集成电路中无故障处理器单元的利用率。本文主要贡献如下:(1)提出了一种处理器阵列横向分块的重构算法,使得内存中的数据利用率提高,总线之间的通信量锐减,运算过程相对连贯,数据重复调用率降低。(2)实现了数据的分块划分与并行处理,执行过程中生成的逻辑子阵列也是可用阵列,根据目标阵列大小的需求,算法可以随时终止。(3)实现了多条逻辑列的并行生成,与现有的算法相比,本文提出的算法是目前运算速度最快的并行重构算法。(4)算法具有良好的可扩展性,更加有利于大规模以及超大规模处理器阵列的重构。
2 容错处理器阵列及重构算法回顾
物理处理器阵列是指多处理器之间以开关链接而成的网状(Mesh)结构,开关功能的转换用来实现物理阵列的逻辑重构。在芯片制造完成后,制造工序中不同环节的可能失误,往往不能保证物理阵列中可用处理器的原始数量。特别是当这种高性能处理器架构应用到航空航天飞行器中时,发射与飞行中的各种不确定因素,不可避免地会引发处理器的故障。 容错技术成为系统可靠性不可或缺的保障。由于阵列结构自身具有潜在的并行处理能力,处理器间的逻辑重构同样可以实现高度的并行化,因此对其容错重构的并行算法研究依然方兴未艾。
在本文中,H表示一个m×n的物理处理器阵列,该阵列可能含有不能工作的处理器单元,这种处理器单元被称为故障处理器单元。ρ表示H上故障处理器单元的比率,从而在物理处理器阵列中正常工作的处理器单元个数N=(1-ρ)·m·n。通过开关状态变化而构造的无故障处理器阵列称为逻辑阵列,记作T。H中出现的行(列)叫做物理行(列),在T中出现的行(列)叫做逻辑行(列)。
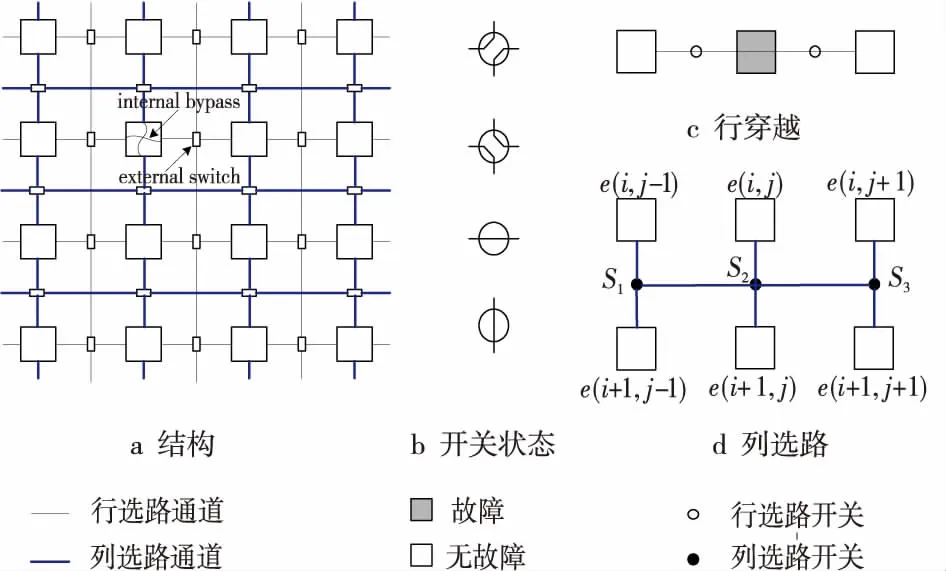
Figure 1 Architecture,switch states and routing schemes图1 容错结构、开关状态和选路方式
图1a给出了一个大小为4×4的物理处理器阵列。相邻的处理器单元(字母e表示)通过开关和链路进行连接。每个开关具有4种状态,如图1b所示。图1中,每个方框代表一个处理器单元,圆圈代表开关。其中灰色方框表示故障处理器单元,白色方框为无故障处理器单元。通过改变处理器单元间的开关状态可使无故障处理器单元之间进行通信,从而使这种结构具有容错性。处理器阵列重构算法通常使用两种控制方案即行穿越和列选路得到逻辑阵列。如图1c所示为行穿越方案,当e(i,j)是故障单元时,e(i,j-1)可以通过e(i,j)中的内部穿越线路和e(i,j+1)进行数据通信。在列选路中,当|j-j′| ≤d时,e(i,j)通过改变相关的开关状态和e(i+1,j′)相连。一般来说,为了减小开关机制的复杂性以及物理实现的代价,应使d越小越好。本文沿用文献[7,8]的规定,即:d≤1。本文定义adj(e)为处理器单元e通过开关状态变化可以连接的列距离小于或等于1的下一行处理器单元的集合。如图1d中所示的列选路,e(i,j)可以通过改变开关,连接第i+1行中的三个处理器单元e(i+1,j-1)、e(i+1,j)和e(i+1,j+1)中的一个。所以adj(e(i,j))={e(i+1,j-1),e(i+1,j),e(i+1,j+1)}。
处理器阵列的常用串行重构算法(记作GCR(Greedy Column Rerouting)[7,8])采用从左至右的方式选择后继单元构造逻辑列,每次迭代产生当前最左的逻辑列,这些逻辑列组成目标阵列。其迭代过程如下:
(1)选取位于第一个物理行上当前最左的无故障处理器单元u作为当前逻辑列的起始点。
(2)选取集合adj(u) 中当前最左的处理器单元v作为处理器单元u的后继点。
在迭代过程中的每一步,GCR算法都试图将当前处理器单元v与位于集合adj(v)中最左的且没有被检测过的处理器单元相连。一旦v在集合adj(v)中找不到可连接的后继单元,即无法通过处理器单元v连接后面的节点形成逻辑列,则算法将回溯到当前处理器单元v的前驱处理器单元w,选择位于集合adj(w)-v中最左的处理器单元作为w的后继点。上述迭代过程持续进行直到以下两种情况:(1)当前位于第k-1行的处理器单元v已与位于最后一行(第k行)上的处理器单元相连;(2)算法回溯到第一行中的某个单元u。GCR算法以从左至右、从上到下的方式构造当前最左逻辑列,直到物理阵列中无法再生成新的逻辑列。GCR算法的详细描述见文献[8]。
目前,最新的并行重构算法是文献[15]提出的PRDC(Parallel Reconfiguration algorithm based on Divide-and -Conquer)算法,其设计思想可递归地描述如下:
在每条逻辑列的生成过程中,将整个逻辑列视作位于上半个物理阵列中的逻辑列段lup与位于下半个物理阵列的逻辑列段ldown的‘归并’对接的结果。这种归并对接操作记作++,即l=lup++ldown。算法递归地生成lup与ldown,直到逻辑列段的长度为1时终止。多个逻辑列段的归并使用同样数目的处理器实现同步并行。PDRC算法的详细描述见文献[15]。
目前,PRDC算法对单条逻辑列的生成实现了并行化,而对于最大目标阵列的多条逻辑列同步并行生成,没有相关算法提出。本文提出的算法就是用来解决多条逻辑列并行生成最大目标阵列问题。
3 阵列分块与多列并行重构
处理器阵列结构本身适合分治算法的应用,它可以被划分成具有相似规模的子块,子块上可以同时进行选路操作,从而提高逻辑阵列的重构速度。基于这个原理,利用分治法潜在的良好并行性,本文提出了处理器阵列分块划分的多逻辑列并行重构算法(记为 MPGCR(Multple Columns Parallel Greedy Reconfiguration)算法)。首先,对整个物理阵列进行横向分块划分;然后在划分后形成的子块上同时采用GCR算法进行选路重构,得到逻辑子阵列;最后并行归并这些逻辑子阵列,得到目标逻辑阵列。
MPGCR算法分为三个过程,分别是阵列分块划分、子阵列重构以及子阵列的归并。具体过程介绍如下。
3.1 阵列分块划分与子阵列重构
在阵列分块划分过程中,初始物理阵列均匀划分成多个物理子阵列。为了准确描述本文的算法,我们对此过程给出如下相关定义。
在子阵列重构过程中,物理子阵列Bi重构出的逻辑子阵列用Ti表示。将p个物理子阵列B0,B1,B2,…,Bp-1分配给p处理器,并行使用GCR生成相应的逻辑子阵列T0,T1,T2,…,Tp-1。
3.2 子阵列的归并
图2给出了4个物理子阵列B0,B1,B2,B3的归并过程。首先,在初次归并过程中,物理子阵列所对应的逻辑子阵列T0,T1,T2,T3被分成{T0,T1},{T2,T3}两组,同时进行子阵列归并,得到更新的目标子阵列T0、T1,然后进行第二次归并,得到目标阵列T0。
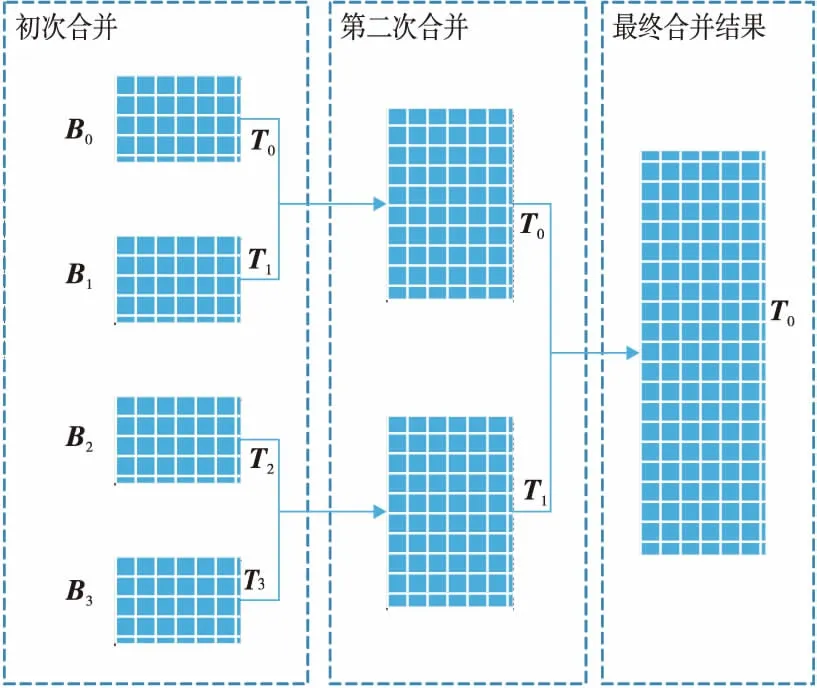
Figure 2 Procedure of merge图2 归并的整体过程
在两个子阵列的具体归并过程中,设相邻逻辑处理器子阵列为Ti、Tj(j=i+1),这两个子阵列上逻辑列段的集合分别为Ci、Cj。设Ci、Cj中分别有x、y个逻辑列段,那么对应的Ci= {Ci,0,Ci,1,Ci.2,…,Ci,x-1},Cj= {Cj,0,Cj,1,Cj,2,…,Cj,y-1}。令处理器单元ei,x、ej,y分别为逻辑列Ci,x、Cj,y的结束断点和开始节点。col(ei,x)、col(ej,y)表示的是逻辑阵列端点ei,x、ej,y所对应的物理阵列的列数。 在归并Ti、Tj的过程中,我们从集合Ci、Cj的最左逻辑列段开始,进行选路操作,归并逻辑列。递归执行这个归并过程,直到没有目标子逻辑列生成为止,最终得到目标逻辑子阵列。
具体目标逻辑子阵列的选路归并操作过程,通过对col(ei,x)、col(ej,y)大小的比较,可分为如下三种情况:
(1)直接选路。
若col(ei,x)=col(ej,y),则这两条逻辑列可以通过直接相连,生成一条逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。
如图3所示,col(ei,1)=col(ej,1),所以在选路时,ei,1与ej,1直接相连,组成了一个大的逻辑列。然后通过对ei,1与ej,2的判断进行下一步选路操作。

Figure 3 Direct_Routing图3 子块直接对接方式
(2)下选路。
若col(ei,x) >col(ej,y),则从ei,x开始通过GCR算法进行下选路。下选路又分为三种情况:
①从ei,x开始选路可以到达Cj,y,则通过这条路径生成一条逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。
如图4a所示,从ei,1点进行GCR选路,与Cj,1上的点有连接,组成了一条大的逻辑列。然后通过对ei,2与ej,2的判断进行下一步选路操作。
②从ei,x开始选路,若不能到达Cj,y,但可以到达Cj,z(假设在逻辑列段中,能够连接的最左逻辑列的列数为z),则通过这条路径生成一条逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。
如图4b所示,从ei,1点进行GCR选路,但是最终没能与Cj,1上的点有连接,而是连接到Cj,2上的点,形成了一条大的逻辑列。然后通过对ei,2与ej,3的判断进行下一步选路操作。
③从ei,x开始选路,未能到达集合Cj中的任何一个逻辑列段,则不能生成逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。
如图4c所示,从ei,1点进行GCR选路,但是最终没能与任何逻辑列上的点有连接,形不成大的逻辑列。然后通过判断ei,2与ej,2进行下一步选路操作。
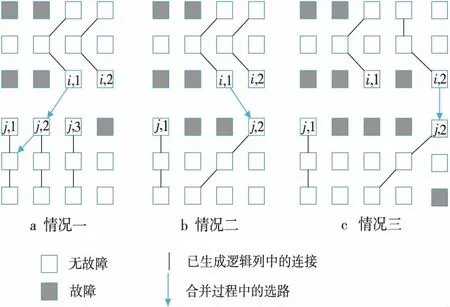
Figure 4 Down_Routing图4 子块下选路方式
(3)上选路。
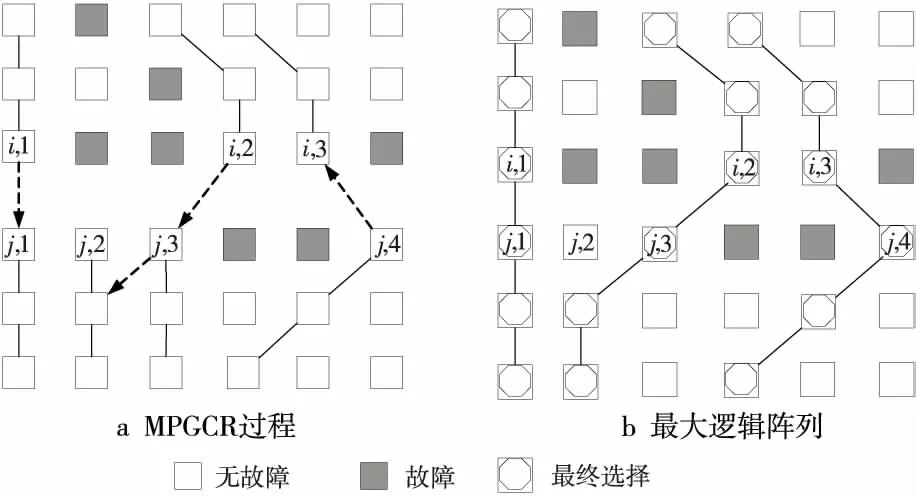
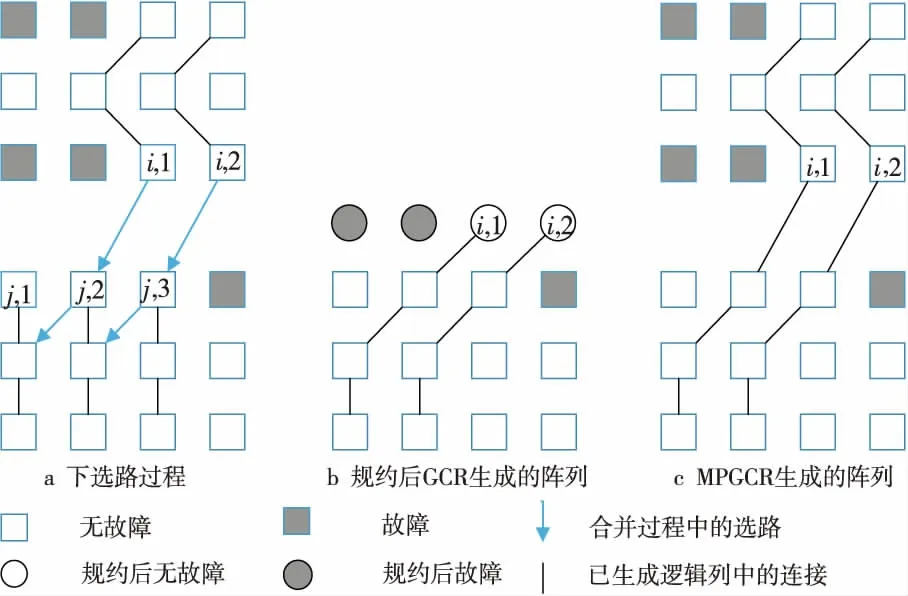
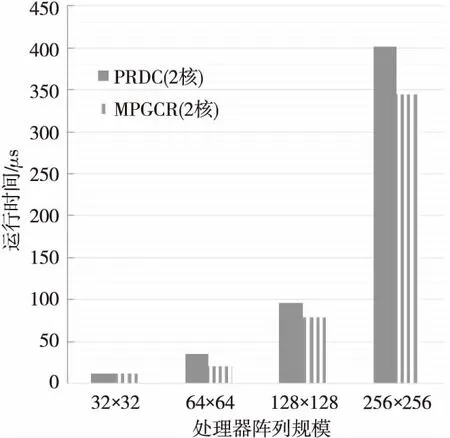
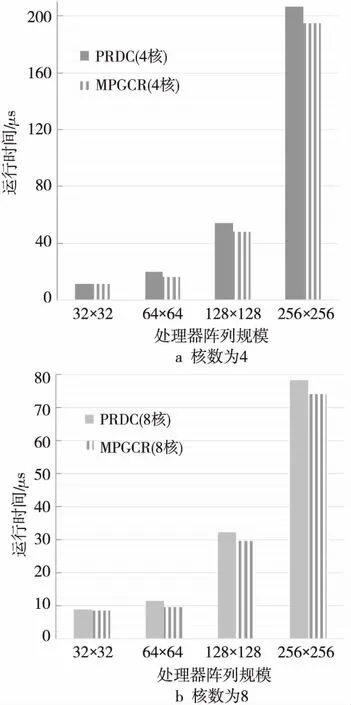
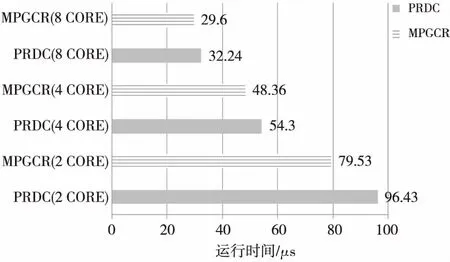
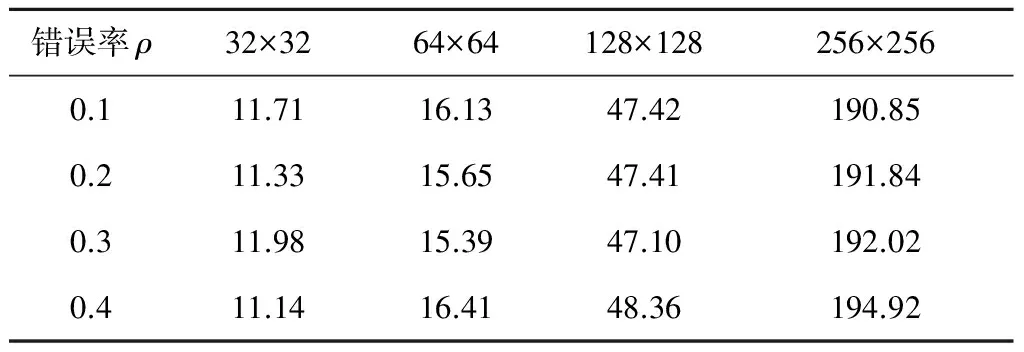
若col(ei,x) ①从ej,y开始选路与Ci,x相交,则生成一条逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。 如图5a所示,从ej,1点进行GCR选路,与Ci,1上的点有连接,组成了一条大的逻辑列。然后通过对ei,2与ej,2的判断进行下一步选路操作。 ②从ej,y开始选路,若不能到达Ci,x,但可以到达Ci,z(假设在逻辑列段中,能够连接的最左逻辑列的列数为z),则通过这条路径生成一条逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。 如图5b所示,从ej,1点进行GCR选路,但是最终没能与Ci,1上的点有连接,而是连接到Ci,2上的点,形成了一条大的逻辑列。然后通过判断ei,3与ej,2进行下一步选路操作。 ③从ej,y开始选路,未能到达集合Ci中的任何一个逻辑列段,则不能生成逻辑列。然后,选择当前已更新逻辑阵列的最左逻辑列段,进行下一条目标逻辑列的生成。 如图5c所示,从ej,1点进行GCR选路,但是最终没能与任何逻辑列上的点有连接,形不成大的逻辑列。然后通过判断ei,2与ej,2进行下一步选路操作。 Figure 5 Up_Routing图5 子块上选路方式 算法的伪代码描述如下: Input:H: physical array ofm×n; B(B0,B1,B2,…,Bp-1):divided block list; T(T0,T1,T2,…,Tp-1):reconstructed subarrays list; p: number of processors. Output:T0: Target array. Algorithm MPGCR(H,B,p) begin /* divideHinto subarrays:B0,B1,B2,…,Bp-1*/ 1. If 0≤i≤p-1 then Bi=(Hi*k,Hi*k+1,Hi*k+2,…,H(i+1 )*k-1)T else Bp-1=(H(p-1)*k,H(p-1)*k+1,H(p-1)*k+2,…,Hm-1)T; /* reconstruct subarrays in parallel */ 2. for each processoriin {0,1,…,p-1} parallel do /* call GCR onBito reconstructTi*/ Ti←GCR(Bi); /* Conquer:block routing to reconstruct final logical array */ 3.num←p; 4. while (num>1) do begin Ti← Merge (T2i,T2i+1); end 5. return; end 算法中的子阵列归并过程的伪代码描述如下: Input:H: Original physical array; Ti、Tj: logical arrays.(j=i+1)。 Output:Ti/2: merged logical array。 Procedure Merge(Ti,Tj) begin 1.Ci←The set of logical segments inTi; 2.Cj←The set of logical segments inTj; 3.N←The size of listCi; 4.M←The size of listCj; /*ei,x、ej,yare the end PE and the start PE ofCi,x、Cj,y,respectively*/ 5. while (x ifcol(ei,x)=col(ej,y) then Direct_Routeing(H,ei,x,ej,y);/*直接选路*/ else ifcol(ei,x)>col(ej,y) then Down_Routeing(H,ei,x,Cj,y);/*下选路*/ else Up_Routeing(H,ej,y,Ci,x);/*上选路*/ end 为了更好地理解MPGCR算法,本文以一个6×6的处理器阵列为例,如图6所示,在2核处理器运行环境下,展示算法并行构造最大逻辑阵列的过程。 首先,整个物理阵列被均匀地分给了2个处理器,每个处理器分得一个3×6的子阵列。然后,2个处理器同时调用GCR算法,构建出对应的逻辑子阵列。如图6a所示,上半部分构建出了3×3的逻辑子阵列;下半部分构建出了3×4的逻辑子阵列。 然后对逻辑子阵列的首尾单元进行标记,进而进行合并操作判断。 处理器单元ei,1,ei,2,ei,3,ej,1,ej,2,ej,3,ej,4分别对应所在逻辑列的列尾单元和列首单元。因为col(ei,1)=col(ej,1),所以直接选路,即ei,1与ej,1直接相连。然后判断ei,2和ej,2,因为col(ei,2)>col(ej,2),所以实施下选路,运用GCR算法从ei,2选路直到遇到Cj,2上的处理器单元为止。因为ei,2连到逻辑列Cj,2和Cj,3,所以接下来判断ei,3与ej,4。因为col(ei,3) 在合并过程结束后,我们就可以得到如图6b所示的6×3最大逻辑阵列。 Figure 6 Construction process of the logical array图6 逻辑阵列的构造过程 本文提出以下引理和定理来证明MPGCR算法和GCR算法能生成同样列数的逻辑阵列(即最大逻辑阵列)。 引理1对于两个阵列,如果它们重构出的逻辑列数分别是x、y,那么将这两个阵列归并后重构出的逻辑列数不超过min{x,y}。 引理2子块上选路或下选路过程重构出的逻辑列个数与物理阵列归并后重构出的逻辑列个数相同。 证明对于两个相邻物理子块Bi、Bj(j=i+1),假设Ci,x、Cj,y是归并过程某一时刻的逻辑列段。假设在下选路过程中,col(Ci,x)>col(Cj,y)。那么下一步是从Ci,x的下端点ei,x进行GCR选路。由于引理1,我们可以将Ci,x逻辑列段规约成下端点ei,x,这个规约并不会减少逻辑列数。子物理块Bi、Bj可以归并成物理子块Bi/2,在这个新的物理块中产生的逻辑列数与我们规约出的新的物理阵列产生的逻辑列数显然是相同的。 □ 如图7a展示出了两个物理子块Bi、Bj的下选路过程。处理器单元ei,1、ei,2分别是逻辑列段Ci,1、Ci,2的下端点。我们将逻辑列段Ci,1、Ci,2规约成端点,没有逻辑列生成的端点都认为是坏点。如图7b展示出了规约形成的物理阵列,经过GCR选路,得到2条逻辑列。图7c是两个物理子块Bi、Bj归并得到的物理阵列,经过GCR选路,也得到了2条逻辑列。 上选路是下选路的反向过程。同理可知,上选路也会生成相同列数的逻辑阵列。所以,子块上选路或下选路过程重构出的逻辑列个数与物理阵列归并后重构出的逻辑列个数相同。 Figure 7 Logical column reduce and Down_Routing图7 逻辑列归约与下选路 定理1MPGCR算法与GCR算法重构出同样列数的目标逻辑阵列。 证明在MPGCR算法中,子阵列划分阶段H被分成B0,B1,B2,…,Bp-1,这个过程没有进行任何重构选路操作,不会影响重构产生逻辑列的个数。子阵列重构阶段,p个子块调用GCR算法并行重构生成p个逻辑子阵列,这个过程中的运算只涉及到GCR算法,所以对生成逻辑列个数也不会产生影响。在子阵列归并阶段,进行了logp次归并操作。在每一次的归并选路过程中,由引理2可知,上选路和下选路都不会减少最终生成的逻辑列数。子块直接对接的情况更不会对生成的逻辑列数产生影响。所以,MPGCR算法与GCR算法重构出同样列数的目标逻辑阵列。 □ 现在我们对算法的时间复杂度进行如下分析:假设阵列规模为m×n,并行重构过程有p个处理器,初始物理阵列被分成p个基本物理子阵列。由p个处理器并行操作,划分过程花费O(1)时间。每个子阵列重构花费时间是O(m·n/p)。最坏情况下,两个具体子阵列归并过程中,每生成一条目标逻辑子列,需要经过m/p(子阵列的行数)次选路操作。在这种情况下,两个具体子阵列归并,最多需要n/(m/p)次目标逻辑子列生成。子阵列的归并总共需进行logp次,所以整个归并过程需要花费时间O((m/p·n)(p/m) logp)=O(nlogp)。 因此,算法的时间复杂度是O(m·n/p+nlogp)。 本文的编程语言为C++,实验环境是AMD A10 PRO-7800B R7,3.50 GHz CPU,4.00 GB RAM,Visual C++ 2010 开发平台。由于并行运算的速度很快,本实验对算法运行时间的测量采用了对程序运行的时钟周期计数的方法,单位为μs。实验结果为测量50次随机实例得到的平均值。 由于文献[15]中的PRDC算法是目前加速比最高的并行算法,且能够生成最大目标逻辑阵列,所以本文提出的算法与PRDC算法进行对比。为客观评价算法的性能,本文采用与文献[15]相同的数据集构建方法,在初始化阵列时使用随机方法产生故障单元,从而保证了实验数据的合理性以及实验结果的可对比性。 从图8可以看出,当阵列错误率为0.4,可用处理器数为2时,MPGCR算法明显快于PRDC算法,并且阵列越大,新算法相对PRDC算法的运算加速,在时间上就越明显。而且,在处理器阵列规模是64×64时,算法性能改进幅度最大。具体来说,在处理器阵列规模是32×32时,新算法相对于PRDC算法快了0.34μs,将PRDC算法改进了2.83%;在处理器阵列规模是64×64时,新算法相对于PRDC算法快了13.91μs,将PRDC算法改进了39.55%;在处理器阵列规模是128×128时,新算法相对于PRDC算法快了16.9μs,将PRDC算法改进了17.53%;在处理器阵列规模是256×256时,新算法相对于PRDC算法快了55.95μs,将PRDC算法改进了13.96%。 Figure 8 Comparisons of running time on using cores图8 核数为2,算法运算时间对比 阵列越大,新算法相对PRDC算法的运算加速,在时间上就越明显。这是因为在可用处理器规模确定的情况下,处理器阵列越大,新算法比PRDC算法分摊到每一个处理器上的通信代价就会越小,处理器每一次运算所用数据中冗余的数据量也会越小。这个实验说明,本文所提出的算法更加适合大规模的处理器阵列重构。 在处理器阵列规模是64×64时,算法性能改进幅度最大。这是因为,现有处理器缓存结构对并行计算存在一个通信瓶颈问题。本文提出的新算法,虽然相对于PRDC算法来说减少了总线通信、数据冗余,但是逻辑单列生成对多条物理列的依赖性,处理器缓存结构的现状,是不可改变的。所以,新算法在2核运算,处理器阵列规模是64×64时,达到通信瓶颈。当阵列规模更大的时候,通信上会有一定阻塞,影响了性能的稳定性。所以,在处理器阵列规模是64×64时,算法性能改进幅度最大。 图9反映了在阵列错误率为0.4时,新、旧算法分别在4核与8核上的运行时间对比。它们的共同规律就是新算法在较大阵列上比原算法在运行时间上改进得相对明显。这说明本文提出的算法具有良好的可扩展性。 Figure 9 Comparisons of running time using 4 cores & 8 cores图9 核数为4和8时,算法运算时间对比 Figure 10 Comparison of running time on 128×128 arrays图10 在128×128阵列上,算法运算时间对比 图10展示了阵列大小固定为128×128,错误率为0.4时,可用处理器数目变化对运行时间的影响。当可用处理器数目为2时,运算速度显著快于PRDC算法。随着参与运算的处理器的增多,本文算法相对于PRDC算法的改进就越少。具体来说,在参与并行重构的处理器数目为2时,MPGCR算法相对于PRDC算法的加速为 17.5%;在参与并行重构的处理器数目为4时,MPGCR算法相对于PRDC算法的加速为 10.9%;参与并行重构的处理器数目为8时,MPGCR算法相对于PRDC算法的加速为 8.2%。 这是因为,在阵列大小固定的情况下,随着可用处理器数目增多,新算法分摊到每一个处理器上的通信代价就会变小,每一个参与并行运算的处理器每一次运算所用数据中冗余的数据量也会变小。 表1是本文MPGCR算法在参与并行重构运算的处理器数目为4,阵列错误率不同且阵列大小不同时,重构阵列所耗费的时间。从表1中可以看出,在不同规模的阵列中,新算法的运行时间对错误率并不敏感。这是因为,算法运行时间包括运算时间以及通信代价,因为通信所耗费的时间在整个运行时间中占据了较大的比例。 Table 1 Running time of MPGCR using4 cores on H128×128 为了更好地展示MPGCR算法的优缺点,我们将其与VHDL并行重构算法[18]进行性能比较。虽然VHDL并行重构算法的扩展性欠佳,也不能确保得到最大逻辑阵列,但是该算法在小规模处理器阵列上的重构速度较快,而且能很好地应用于FPGA并行运算。由文献[18]可知,VHDL并行重构算法在物理阵列为48×48时,加速比达到最大。由于VHDL并行重构算法重构大小为48×48的物理阵列时,使用24个核(实验所用的CPU支持单核双线程)参与并行运算,最能直观地反映出VHDL算法的并行特性。因此,我们计算了在24核并行运算时,MPGCR算法在不同规模处理器阵列下所能达到的加速比,并引用VHDL并行重构算法的结果进行对比。表2是MPGCR算法与VHDL并行重构算法,在24核并行运算时的加速比。 Table 2 Speed up of MPGCR and VHDL parallelreconfiguration algoritym using 24 cores 表2中“*”表示实验在当前条件下不能得到数据。 从表2可以看出,在小规模处理器阵列上,MPGCR算法的加速比低于VHDL并行重构算法,这是因为VHDL算法是启发式算法,不能保证得到最大的逻辑子阵列。MPGCR算法具有良好的可扩展性,能够在较大阵列上得到良好的加速比,加速比随着阵列大小的增加而呈现上升趋势,并且能够确保得到最大的逻辑子阵列。 本文根据网格开关连接处理器阵列结构的潜在并行性,提出了一种新的处理器阵列划分方式,使用分治法,设计了一种可以多条逻辑列并行重构的算法。算法在有很好并行性的同时,减少了通信以及计算的数据冗余。实验结果表明,与现有的并行重构算法相比,MPGCR算法同样能生成最大规模的目标阵列并且当物理阵列大小为64×64,错误率为0.4,2核并行运算时,与现有算法对比,新算法并行重构速度提高了39.5%。 [1] Lam C W H,Li H F,Jayakumar R.A study of two approaches for reconfiguring fault-tolerant systolic arrays[J].IEEE Transactions on Computers,1989,38(6):833-844. [2] Chen Y Y, Upadhyaya S J,Cheng C H.A comprehensive reconfiguration scheme for fault-tolerant VLSI/WSI array processors[J].IEEE Transactions on Computers,1997,46(12):1363-1371. [3] Zhang L.Fault-tolerant meshes with small degree[J].IEEE Transactions on Computers,2002,51(5):553-560. [4] Horita T, Takanami I. Fault-tolerant processor arrays based on the 1 1/2-track switches with flexible spare distributions[J].IEEE Transactions on Computers,2000,49(6):542-552. [5] Zhang L,Han Y,Xu Q,et al.On topology reconfiguration for defect-tolerant NoC-based homogeneous manycore systems[J].IEEE Transactions on Very Large Scale Integration Systems,2009,17(9):1173-1186. [6] Kuo S Y,Chen I Y.Efficient reconfiguration algorithms for degradable VLSI/WSI arrays[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2006,11(10):1289-1300. [7] Low C P,Leong H W.On the reconfiguration of degradable VLSI/WSI arrays[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,1997,16(10):1213-1221. [8] Low C P.An efficient reconfiguration algorithm for degradable VLSI/WSI arrays[J].IEEE Transactions on Computers,2000,49(6):553-559. [9] Fukushi M, Horiguchi S.Reconfiguration algorithm for degradable processor arrays based on row and column rerouting[C]∥Proc of the 19th IEEE International Symposium on Defect and Fault Tolerance in VLSI Systems,2004:496-504. [10] Fukushi M, Fukushima Y,Horiguchi S.A genetic approach for the reconfiguration of degradable processor arrays[C]∥Proc of IEEE International Symposium on Defect & Fault Tolerance in VLSI & Nanotechnology Systems,2005:63-71. [11] Jigang W, Srikanthan T. Reconfiguration algorithms for power efficient VLSI subarrays with four-port switches[J].IEEE Transactions on Computers,2006,55(3):243-253. [12] Jigang W,Srikanthan T,Han X.Preprocessing and partial rerouting techniques for accelerating reconfiguration of degradable VLSI arrays[J].IEEE Transactions on Very Large Scale Integration Systems,2010,18(2):315-319. [13] Zhu Y,Wu J,Lam S K,et al.Reconfiguration algorithms for degradable VLSI arrays with switch faults[C]∥Proc of IEEE International Conference on Parallel & Distributed Systems,2012:356-361. [14] Shen Y, Wu J,Jiang G.Multithread reconfiguration algorithm for mesh-connected processor arrays[C]∥Proc of International Conference on Parallel and Distributed Computing,Applications and Technologies,2012:659-663. [15] Wu J, Jiang G,Shen Y,et al.Parallel reconfiguration algorithms for mesh-connected processor arrays[J].Journal of Supercomputing,2014,69(2):610-628. [16] Jiang G,Wu J,Sun J.Efficient reconfiguration algorithms for communication-aware three-dimensional processor arrays[J].Parallel Computing,2013,39(9):490-503. [17] Jiang G,Wu J,Sun J.Non-backtracking reconfiguration algorithm for three-dimensional VLSI arrays[C]∥Proc of 2013 International Conference on Parallel and Distributed Systems,2012:362-367. [18] Zhou Mei-ting,Wu Ji-gang,Jiang Gui-yuan.Parallel reconfiguration for processor arrays with faults utilizing VHDL[J].Journal of Chinese Computer Systems,2015,36(2):375-380.(in Chinese) 附中文参考文献: [18] 周美婷,武继刚,姜桂圆.容错处理器阵列的并行重构及VHDL实现[J].小型微型计算机系统,2015,36(2):375-380.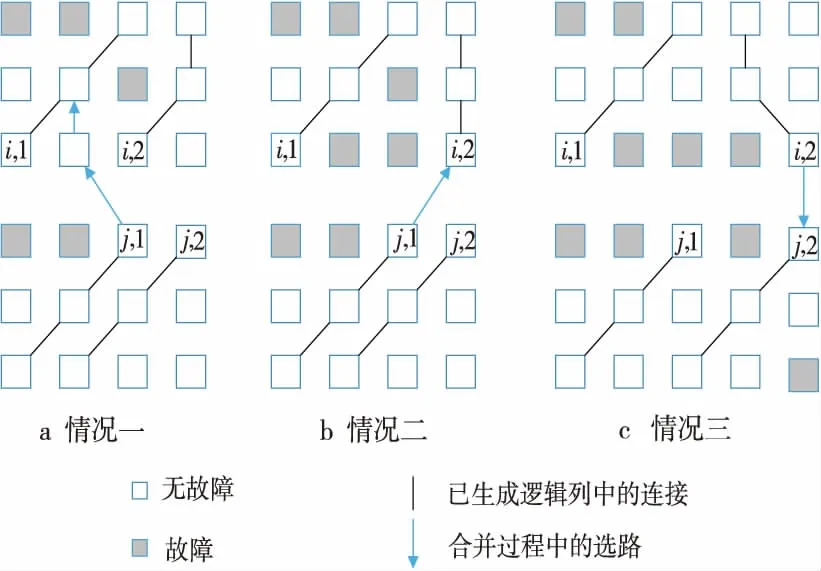
3.3 算法分析
4 实验结果与分析

5 结束语
