基于人工蜂群优化的密度聚类异常入侵检测算法
2018-01-26任维武张波辰底晓强卢奕南
任维武, 张波辰, 底晓强, 卢奕南
(1. 长春理工大学 计算机科学技术学院, 长春 130022; 2. 吉林大学 计算机科学与技术学院, 长春 130012)
随着移动智能终端设备的大规模普及, 移动芯片已逐渐接近甚至达到了桌面级计算机的计算和处理能力, 而且搭载在移动终端上的各类应用进一步扩大了终端的使用范围. 移动智能设备的“电脑化”, 不但给自身带来了传统计算机系统的各类安全威胁, 而且还增加了自身独有的更复杂、 更具挑战性的安全风险. 入侵检测系统是一种经典有效的防御技术, 对保护全球信息基础设施发挥了巨大作用. 入侵检测通过计算机系统或网络中若干节点的收集和分析审计记录、 安全日志、 用户行为及网络数据等信息, 检查网络或系统中是否存在违反安全策略的入侵行为及被攻击的迹象[1]. 根据检测机制不同, 可以将入侵检测系统分为误用检测和异常检测. 误用检测精度高, 误报率低, 但不能检测未知入侵行为; 异常检测通过建立正常的用户和系统行为轮廓, 能检测未知入侵行为, 但误报率一般较高. 根据训练数据源的不同, 可以将入侵检测系统分为有监督和无监督. 有监督方法能够从标记数据集中发现与标记示例近似的入侵或正常行为, 如决策树、 神经网络、 支持向量机(SVM)等; 无监督方法能够从无标记数据集中发现隐藏的结构性知识, 即不同于正常行为的异常行为, 如聚类方法[2]等.
目前针对安卓平台的安全性研究成果较多, 如Shabtai等[3]通过提出一个基于主机恶意行为的检测框架, 建立机器学习异常检测器来识别正常行为和异常行为; Reina等[4]提出了自动动态分析安卓异常行为的方法, 该方法通过分析底层的QS特征行为(如读写文件、 执行程序等)及高层的安卓特征行为(如存取个人信息、 发送信息等), 利用一系列的系统调用判定行为属性; Enck等[5]提出了实时监控用户隐私的信息流跟踪系统, 针对敏感信息如信息数据、 邮件数据、 电话数据等进行实时监控; Burguera等[6]提出了一种安卓异常行为检测系统, 由两部分组成: 需要安装的源APP和一个远程的恶意检测服务器, 源APP发送特征数据到远程服务器, 由远程服务器进行鉴别.
人工蜂群(artificial bee colony, ABC)算法[7]通过模拟蜜源搜索、 采蜜分工、 信息分享等蜜蜂采蜜过程, 实现目标问题的随机优化. 相比其他随机优化算法, 如遗传算法、 蚁群算法和模拟退火算法等, 其优点是兼顾了全局搜索和局部搜索, 使得解搜索和解选择达到了较好的平衡. 目前人工蜂群算法研究主要集中于算法在不同领域的应用和对算法本身的改进两方面. 在聚类分析应用中, Karaboga等[8]利用数据不同属性寻找它们的相似性, 对多变量数据聚类有较好的效果.
聚类是一种无监督异常算法, 能在没有任何先验知识的前提下发现未知攻击, 典型的聚类算法包括DBSCAN算法[9]、 OPTICS算法[10]和DENCLUE算法[11]等, 其中DBSCAN算法的聚类速度快, 参数较少, 只有两个全局变量的参数Eps和Minipts, 且能在含有噪声空间的数据中发现任意形状的簇, 生成的正常行为轮廓精度较高, 因此, 改进后的DBSCAN算法是一种较优良的异常入侵检测算法. 虽然DBSCAN算法只有两个参数, 但在实际应用中, 确定参数Eps和Minipts十分困难, 如果选取不当, 就会生成精度较差的正常行为轮廓, DBSCAN算法提供了一种可视化辅助确定Eps的方法, 但这种方法确定的Eps通常不是最优参数, 聚类效果并不稳定. 此外, DBSCAN算法具有一定的抗噪声能力, 但异常检测数据通常涉及多个特征属性, 有些特征属性不能有效地代表业务逻辑和业务场景, 甚至有些特征属性本身即为噪声, 训练生成的行为轮廓可能将噪声特征作为正常行为特征, 影响了真实输入与输出间的关系, 导致过拟合现象, 影响最终的检测效果. 基于这两个问题, 本文提出一种基于人工蜂群优化的密度聚类异常入侵检测(ABC-DBSCAN)算法, 利用人工蜂群对密度聚类的参数和特征属性进行组合优化, 以实现检测性能的最终提升.
1 预备知识
初始化蜜源: 在使用ABC算法求解优化时, 每个蜜源都代表问题的一个优化组合解. 设ABC算法随机初始化N个蜜源(解), 则蜜源xi可表示为
xi=lb+(ub-lb)×rand(0,1),
(1)
其中:xi(i=1,2,…,N)表示第i个蜜源;lb和ub分别表示x取值范围的上限和下限.xi可以用一个D维向量表示, 其中xij(j=1,2,…,D)为蜜源i的第j个待优化参数. 当xij为离散二值时, 参数xij表示为
(2)
领域搜索: 引领蜂和跟随蜂对蜜源领域进行搜索, 蜜源的每个参数均被搜索, 其搜索过程可表示为
=xij+(xij-xkj)×rand(-1,1),
(3)
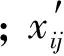
(4)
蜜源选择: 跟随蜂根据蜜源概率采蜜, 概率大的蜜源被采的可能性也大, 反之亦然. 蜜源选择公式表示为
(5)
其中: Prob(i)表示第i个蜜源被选择的概率; fit(i)表示第i个蜜源的适应值; fitmax表示最大适应值. 适应值越高, 概率越大.
适应值: 入侵检测系统的检测性能评价参数主要有两个, 即检测率DR(detection rate)和误报率FPR(false positive rate), 检测率越高越好, 误报率越低越好, 所以可以将适应值定义为
fit(i)=DR+(1-FPR)×γ-d/D,
(6)
其中:γ为误报率影响因子, 可以根据实际需要, 提高误报率的权值;d为蜜源特征数. 检测率:
(7)
其中: TAs表示正确报警的入侵数; Is表示总的入侵样本数. 误报率:
(8)
其中: FAs为错误报警数; Ts为总样本数.
随机搜索: 如果经过最大限制次搜索后, 解未得到改善, 则引领蜂变为侦察蜂, 并随机产生一个新解, 可表示为
xij=lbj+(upj-lbj)×rand(0,1),
(9)
当xij为离散二值时, 新解可表示为
(10)
MSN表示算法经过一定次数的迭代后, 适应值没有改善, 则该蜜源被放弃.
2 主要算法
人工蜂群算法包括蜜源初始化过程、 引领蜂搜索过程、 跟随蜂选择过程和侦察蜂搜索过程. 将其与异常检测的过程整合优化后如图1所示. 由于本文提出的改进算法涉及到异常检测算法参数优化和特征选择两方面, 因此其中既有连续值的优化, 也有离散值的选取. 此外, 选择适应值一定要遵循提高算法检测性能的原则, 所以本文主要从初始化蜜源、 邻域搜索和适应值计算等三方面介绍改进算法的特有优化过程.

图1 算法流程Fig.1 Flow chart of algorithm
1) 初始化蜜源. 在使用ABC算法求解最优化问题时, 每个蜜源都代表问题的一个优化组合解, 本文方法中, 蜜源由两部分组成: 参数部分和特征部分. 参数部分采用连续值编码, 特征部分采用离散二值编码. 密度异常检测算法有两个主要参数Eps和Minipts, 这两个参数是连续值, 取值范围受聚类规模影响, 生成蜜源时可参考式(1). 算法的训练和测试数据样本有106个特征, 对这些特征可采用遗传算法的编码机制, 利用一个长度为106位的二进制串表示, 若当前位取值为1, 则表示选择该特征, 若当前位取值为0, 则表示删除该特征. 采用这种编码机制的解每一位都是离散二值的, 生成蜜源时可参考式(2).
2) 适应值计算. 每个蜜源都有自己的适应值, 用于评价蜜源的优劣. 在密度聚类异常算法中, 蜜源的适应值表示当前参数和特征组合的检测性能. 评价入侵检测算法检测性能的指标很多, 常见的有检测率、 误报率和实时性等, 检测率越高、 误报率越低、 实时性越好的检测算法越能成为优秀入侵检测系统的核心算法. 本文只考虑最主要的两个指标: 检测率和误报率, 其中检测率的定义如式(7), 误报率的定义如式(8). 由于检测原理等方面的原因, 高误报率是制约异常检测算法发展的主要瓶颈, 高误报率会导致入侵检测系统频繁地报警, 而多数警报是虚警, 会给系统管理员产生大量不必要的麻烦. 因此, 异常检测算法检测性能的评价原则是在保证检测率的前提下, 尽量降低误报率. 基于此, 适应值定义为式(6), 并且本文设计了一个误报率影响因子γ, 可以根据不同入侵检测系统对误报率的需求, 提高或降低误报率影响因子γ, 以达到放大或缩小误报率在整体适应值上的影响.
3) 邻域搜索. 引领蜂和跟随蜂对蜜源的邻域进行搜索, 根据蜜源组成不同, 搜索也分为参数部分和特征部分. 参数部分是连续值, 搜索方法可按式(3)对Eps和Minipts两个参数的邻域进行随机搜索; 特征部分是离散值, 搜索方法可按式(4)对106维特征空间的邻域进行随机搜索. 算法伪代码如下.
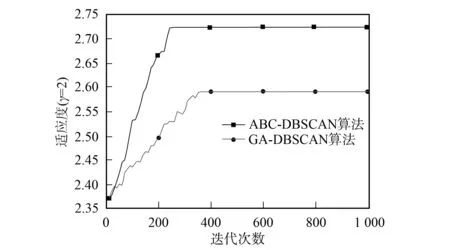
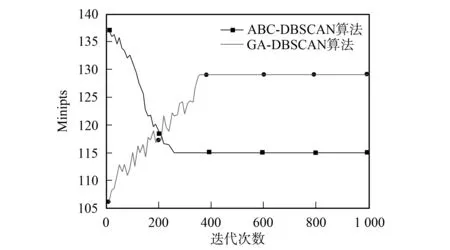
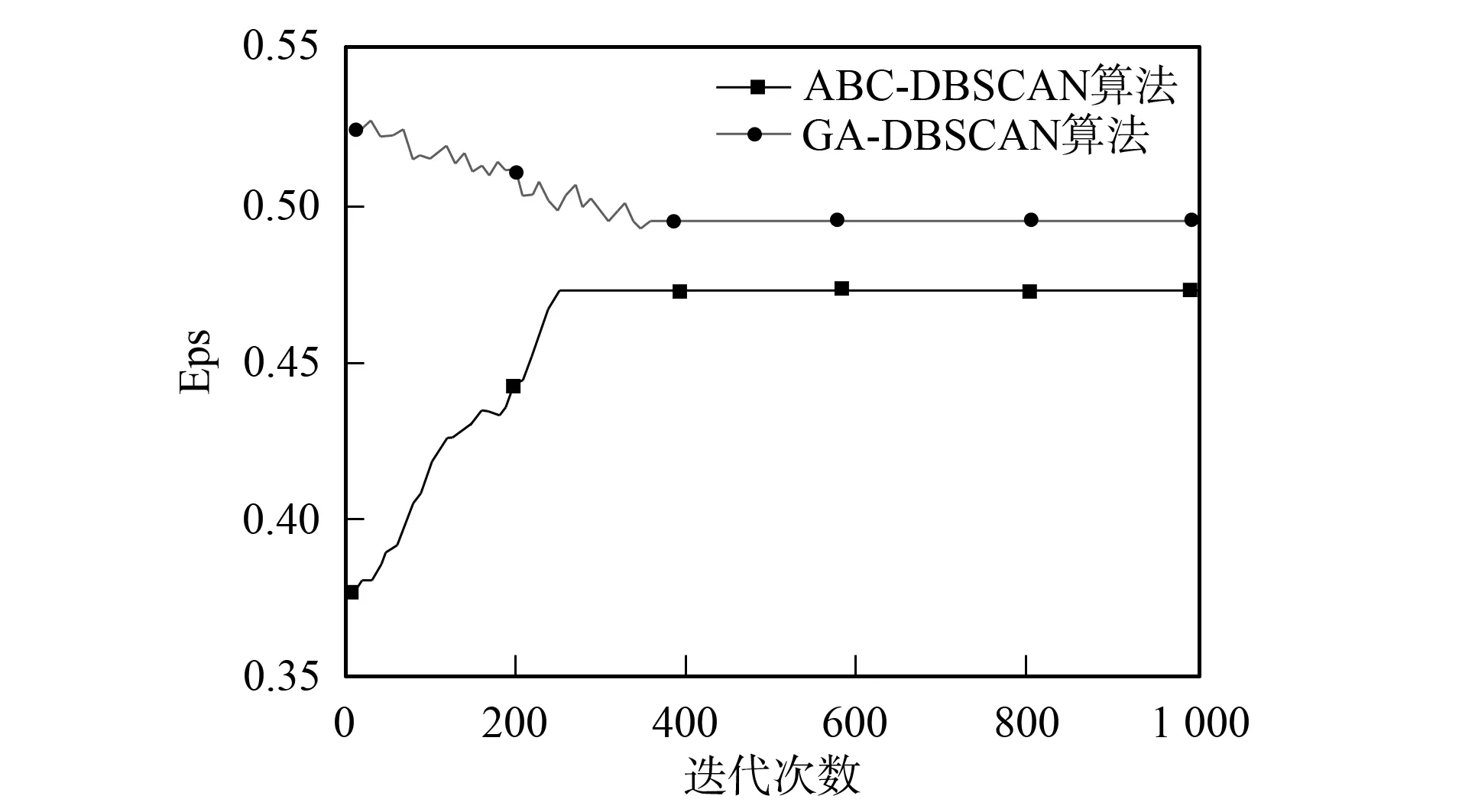
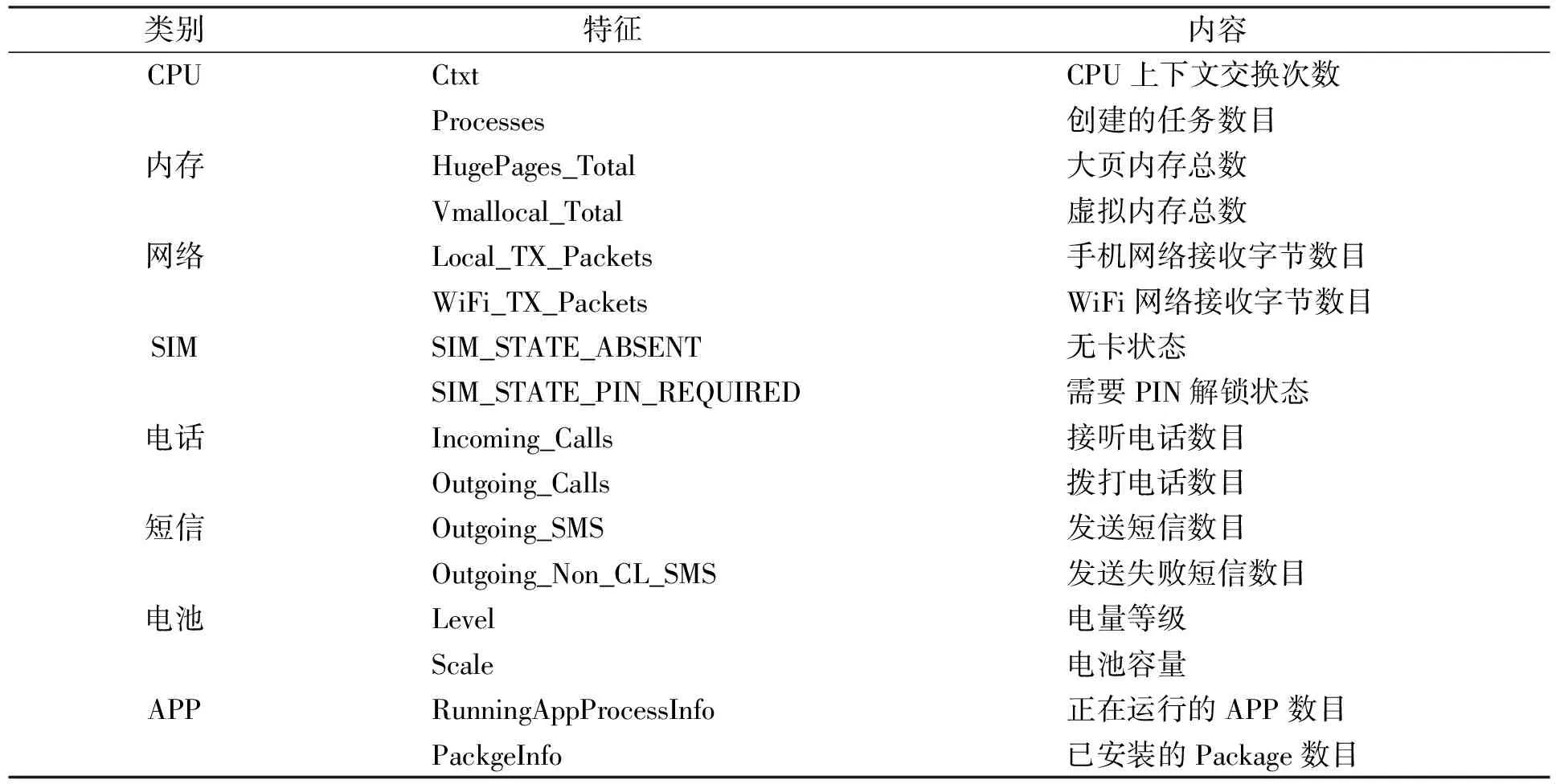
WhileI Initialize (xi) 根据式(1),(2)随机初始化N个蜜源 Calculatefit(xi) 根据式(6)计算每个蜜源的适应值 While Iter Whilei Whilej Initialize(xij) 根据式(3),(4)邻域搜索(引领蜂), 生成新蜜源 Calculatefit(xi) 根据式(6)计算新蜜源的适应值 Maxfit(xi) 贪婪法选择最优解 Prob(xi) 根据概率选择蜜源 Whilej Initialize(xij) 根据式(3),(4)邻域搜索(跟踪蜂), 生成新蜜源 Calculatefit(xi) 根据式(6)计算新蜜源的适应值 Maxfit(xi) 贪婪法选择最优解 If>MSN Initialize(xi) 根据式(9),(10)随机搜索(侦察蜂), 生成新蜜源 If iter>C Current optimal solution 大于迭代次数, 输出当前最优解 实验数据源于一台红米NOTE1手机, 其配置为四核1.6 GHz, 内存为2.0 GB, 操作系统为MIUI8.0.1.0(已root), 正常行为数据源于用户日常使用行为收集, 异常行为主要来自于特定时间段内对Android Malware Genome Project项目(http://www.malgenomeproject.org/)和卡饭论坛(http://bbs.kafan.cn/forum-31-1.html)APK病毒样本数据收集. 特征选取参考文献[3-4,6], 对于文献的特征[6], 都已加入本文的数据中, 而由于安卓平台版本更迭, 一些新特征也被加入, 数据包含106个特征, 主要分为8个类别: CPU、 内存、 网络、 SIM、 电话、 短信、 电池、 APP, 部分特征列于表1. 一条数据为一段时间内特征的累计值或平均值, 时间片T=500 ms. 表1 部分特征列举 算法的重要参数有两个: MSN和γ. MSN表示经过一定次数(MSN次)的迭代后, 解并未发生明显改善, 则重新进行随机搜索. 如果MSN取值过小, 则收敛速度慢, 随机性变强, 但搜索空间变大, 容易找到最优解; 如果MSN取值过大, 则收敛速度快, 随机性变弱, 但容易陷入局部最优. 本文选取参数MSN=10, 这样选取会导致收敛速度较慢, 但放出的侦查峰变多, 搜索空间变大. 为了提高检测效果, 本文更注重最优解, 收敛速度慢可容忍.γ为误报率影响因子, 一般认为异常检测算法更注重误报率, 在保证一定检测率的基础上, 更低的误报率通常会有更好的用户体验, 因此本文选取γ=2. 图2 适应度与迭代次数的关系Fig.2 Relationship between fitness and number of iterations 图2为适应度与迭代次数关系曲线. 由图2可见: 每10次迭代输出最后一次的适应度值, 经过240次迭代后, ABC-DBSCAN算法的适应值收敛, 而经过350次迭代后, GA-DBSCAN算法的适应值收敛; 比较两种算法的收敛值, ABC-DBSCAN算法的收敛值更好, 检测效果更好; 比较两种算法的收敛速度, ABC-DBSCAN算法的收敛速度更快, 能在更短的时间内找到最优解. 图3为Minipts与迭代次数关系曲线. 由图3可见: 经过260次迭代后, ABC-DBSCAN算法的Minipts收敛, 而经过360次迭代后, GA-DBSCAN算法的Minipts收敛; 比较两种算法的收敛速度, ABC-DBSCAN算法的收敛速度更快. 图4为Eps与迭代次数关系曲线. 由图4可见: 经过260次迭代后, ABC-DBSCAN算法的Eps收敛, 而经过350次迭代后, GA-DBSCAN算法的Eps收敛; 比较两种算法的收敛速度, ABC-DBSCAN算法的收敛速度更快. 表2为3种算法的性能比较. 图3 Minipts与迭代次数的关系Fig.3 Relationship between Minipts and number of iterations 图4 Eps与迭代次数的关系Fig.4 Relationship between Eps and number of iterations 算法DBSCANABC⁃DBSCANGA⁃DBSCAN检测效果(检测率/误报率)/%72.5/8.183.2/5.474.2/7.8特征数量1062342 由表2可见: 与无优化的原始算法相比, ABC-DBSCAN算法收敛后特征数降至23维, 检测率更高, 误报率更低; 与GA-DBSCAN算法相比, ABC-DBSCAN算法不仅特征数量更少, 而且检测效果也有一定优势. 综上所述, 本文提出的基于人工蜂群优化的密度聚类异常入侵检测算法, 解决了基于密度聚类异常检测算法的参数优化和特征选择问题. 该算法能在较短的时间内在106维的特征空间中找到最优的特征子集, 并找到合适的Minipt和Eps, 使得算法的检测性能达到最优. 此外, 误报率影响因子的加入, 使算法在保证一定检测率的基础上误报率更低. [1] 杨宏宇, 朱丹, 谢丰, 等. 入侵异常检测研究综述 [J]. 电子科技大学学报, 2009, 38(5): 587-592. (YANG Hongyu, ZHU Dan, XIE Feng, et al. The Research Summary of Intrusion Detection [J]. Journal of University of Electronic Science and Technology of China, 2009, 38(5): 587-592.) [2] 胡亮, 任维武, 任斐, 等. 基于改进密度聚类的异常检测算法 [J]. 吉林大学学报(理学版), 2009, 47(5): 954-960. (HU Liang, REN Weiwu, REN Fei, et al. Anomaly Detection Algorithm Based on Improved Density Cluster [J]. Journal of Jilin University (Science Edition), 2009, 47(5): 954-960.) [3] Shabtai A, Kanonov U, Elovici Y, et al. “Andromaly”: A Behavioral Malware Detection Framework for Android Devices [J]. Journal of Intelligent Information Systems, 2012, 38(1): 161-190. [4] Reina A, Fattori A, Cavallaro L. A System Call-Centric Analysis and Stimulation Technique to Automatically Reconstruct Android Malware Behaviors [C]//EuroSec. New York: ACM, 2013: 1-6. [5] Enck W, Gilbert P, Han S, et al. TaintDroid: An Information-Flow Tracking System for Realtime Privacy Monitoring on Smartphones [C]//10th Usenix Conference on Operating Systems Design & Implementation. New York: ACM, 2010: 393-407. [6] Burguera I, Zurutuza U, Nadjm-Tehrani S. Crowdroid: Behavior-Based Malware Detection System for Android [C]//ACM Workshop on Security & Privacy in Smartphones & Mobile Devices. New York: ACM, 2011: 15-26. [7] Karaboga D. An Idea Based on Honey Bee Swarm for Numerical Optimization [EB/OL]. [2016-11-01]. http://www.dmi.unict.it/mpavone/nc-cs/materiale/tr06_2005.pdf. [8] Karaboga D, Ozturk C. A Novol Clustering Approach: Artificial Bee Colony (ABC) Algorithm [J]. Applied Soft Computing, 2011, 11(1): 652-657. [9] Birant D, Kut A. ST-DBSCAN: An Algorithm for Clustering Spatial-Temporal Data [J]. Data & Knowledge Engineering, 2007, 60(1): 208-221. [10] Ankerst M, Breuniq M M, Krieqel H P, et al. OPTICS: Ordering Points to Identify the Clustering Structure [J]. ACM Sigmod Record, 1999, 28(2): 49-60. [11] Hinneburg A, Gabriel H H. DENCLUE 2.0: Fast Clustering Based on Kernel Density Estimation [C]//International Symposium on Advances in Intelligent Sata Analysis. New York: ACM, 2007: 70-80.3 实验结果与讨论
3.1 数据来源
3.2 结果分析