有限群稳定模范畴的Bousfield等价

黄 文 林

(中国人民大学 信息学院, 北京 100872)

0 引 言

目前, 关于稳定同伦范畴谱上等价关系[1-3]的研究已成为拓扑学、 代数几何、 群与代数表示论的共同研究课题[1-7]. Bousfield类是研究张量三角范畴局部化子范畴的重要途径. 稳定同伦范畴、 交换环的导出范畴、 稳定模范畴都是张量三角范畴. 在张量三角范畴中, 一般地, Bousfield类是局部化子范畴； 反之, 并不是每个局部化子范畴都是一个Bousfield类. 但对于有限群G的稳定模范畴StMod(kG)(其中k是一个域), 其局部化子范畴即为其Bousfield类[4]. StMod(kG)及其满子范畴Stmod(kG)(全体有限生成kG-模的稳定范畴)在有限群表示论中应用广泛.

本文考虑Stmod(kG)的Bousfield类, 可视为StMod(kG)的Bousfield类在Stmod(kG)中的部分. 并考虑Bousfield等价关系, 证明了若H是G的强p-嵌入子群, 则(不可分解)kG-模M与N是Bousfield等价的当且仅当其限制模(Green对应)是Bousfield等价的, (不可分解)kH-模U和V是Bousfield等价的当且仅当其诱导模(Green对应)是Bousfield等价的, 以及Green对应诱导了Stmod(kG)的全体Bousfield等价类与Stmod(kH)的全体Bousfield等价类之间的一一对应. 本文假设G是阶含有素数因子p的有限群,k是特征为p的数域, 若无特别说明, 所有的模均是有限生成的. 其他记号和术语参见文献[7-8].

1 Stmod(kG)的Bousfield类

文献[9]给出了稳定模范畴StMod(kG)及其满子范畴Stmod(kG)的构造方法, StMod(kG)和Stmod(kG)都是紧生成的三角范畴. 对于任意的kG-模V和W(不一定是有限生成的), 以及任意的g∈G,v∈V,w∈W, 按G-作用：g(v⊗kw)∶=gv⊗kgw,k-张量积V⊗W做成一个kG-模, 称为V和W的张量模. 在该张量积下, (StMod(kG),⊗,k)是一个张量三角范畴[7], 而(Stmod(kG),⊗,k)是其张量三角子范畴. 显然, 可得以下结论:

引理1设M是kG-模, 则在稳定模范畴Stmod(kG)中,M=0当且仅当M是投射kG-模.

定义1[6]设M是(有限生成的)kG-模, 在Stmod(kG)中, 记〈M〉∶={(有限生成的)kG-模X|M⊗X=0}, 并称〈M〉为有限群G的稳定模范畴Stmod(kG)的Bousfield类.

注1由引理1可知, 〈M〉={X|X是(有限生成的)kG-模,M⊗X是(有限生成的)投射kG-模}.

注2StMod(kG)的Bousfield类可类似定义[6], Stmod(kG)的Bousfield类是StMod(kG)的Bousfield类与Stmod(kG)的交.

注3对于任意kG-模M, Stmod(kG)的Bousfield类〈M〉是张量三角范畴Stmod(kG)张量闭的三角子范畴.

显然, 可得以下结果.

引理2设M是kG-模, 则在Stmod(kG)中, 下列结论成立:

1) 〈0〉=Stmod(kG)；

2) 〈k〉={X|X是投射kG-模}；

3) 〈k〉⊆〈M〉⊆〈0〉.

引理3设M和N是kG-模, 则在Stmod(kG)中, 下列结论成立:

1) 〈M⊕N〉=〈M〉∩〈N〉；

2) 〈M⊗N〉⊇〈M〉∪〈N〉.

性质1设M是kG-模, 则在Stmod(kG)中, 下列结论成立:

1) 〈M*〉=〈M〉；

2) 〈Ω(M)〉=〈M〉.

证明： 1) 因为M是有限生成的, 所以M|M⊗M*⊗M. 由引理3知, 〈M*〉⊆〈M⊗M*⊗M〉⊆〈M〉, 即〈M*〉⊆〈M〉. 又因为文献[8]中性质8.5.1给出M≅(M*)*, 并且在张量三角范畴Stmod(kG)中, -⊗X是正合函子, 所以M⊗X与(M*)*⊗X在Stmod(kG)中同构, 表明〈M〉=〈(M*)*〉. 综上可得, 〈M*〉=〈M〉.

2) 一方面, 对于任意的X∈〈M〉,M⊗X是投射kG-模, 结合文献[8]中性质11.7.2知,Ω(M)⊗X=Ω(M⊗X)⊕S=S, 这里S是一个投射kG-模, 因此X∈〈Ω(M)〉, 〈M〉⊆〈Ω(M)〉. 另一方面, 设Y∈〈Ω(M)〉, 则Ω(M)⊗Y是投射kG-模, 再结合文献[8]中性质11.7.2知,Ω(M)⊗Y=Ω(M⊗Y)⊕T, 这里T是一个投射kG-模, 表明Ω(M⊗Y)=0, 从而M⊗Y是投射kG-模,Y∈〈M〉, 〈Ω(M)〉⊆〈M〉. 证毕.

性质1表明,kG-模M的对偶M*和Heller变换Ω(M)的Bousfield类与M的Bousfield类相同.

引理4设M是kG-模, 则在Stmod(kG)中, 〈M⊗M〉=〈M〉.

证明： 由文献[5]中例6.10和文献[4]中例2.14知, 结论成立. 此外, 由性质1知, 一方面, 〈M*〉=〈M〉, 则〈M⊗M*〉=〈M⊗M〉; 另一方面, 〈M⊗M*〉⊆〈M⊗M*⊗M〉⊆〈M〉. 综上可得, 〈M⊗M〉=〈M〉.

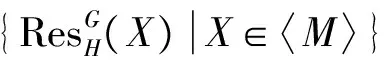
2 Stmod(kG)的Bousfield等价

定义2[6]对于(有限生成的)kG-模M和N, 若在Stmod(kG)中, 〈M〉=〈N〉, 则称M与N是Bousfield等价的, 记为M～N.M所在的Bousfield等价类记为《M》, 稳定模范畴Stmod(kG)的全体Bousfield等价类记为(kG).

引理5设M和N是kG-模, 则下列结论成立:

1) 若M与N在Stmod(kG)中同构, 则M～N；

2) 若M≅N, 则M～N.

证明： 1) 对于任意kG-模X, 在Stmod(kG)中, -⊗X是正合函子, 所以在Stmod(kG)中M⊗X与N⊗X同构, 表明X∈〈M〉当且仅当X∈〈N〉, 即〈M〉=〈N〉,M～N.

2) 若M≅N, 则M与N在Stmod(kG)中也同构, 由1)可知2)成立.

注4引理5表明, Bousfield等价不仅是kG-模上的等价关系, 还是kG-模同构关系的弱化.

可裂迹kG-模在有限群的模上几乎可裂序列中应用广泛.

引理6设M是kG-模, 则下列结论成立:

1)M～0当且仅当M是投射kG-模；

2) 进一步, 若M是可裂迹kG-模, 则M～k.

证明： 1) 若M是投射kG-模, 由引理1知, 〈M〉=〈0〉=Stmod(kG)； 反之, 若M～0, 则k∈〈M〉, 表明M是投射kG-模.

2) 若M是可裂迹kG-模, 则M*⊗M≅End(M)=k⊕U, 这里U是一个kG-模. 此时, 对任意的X∈〈M〉,M⊗X是投射kG-模, 因此,M*⊗M⊗X≅X⊕(X⊗U)也是投射kG-模, 从而X也是投射kG-模. 结合引理2知, 〈M〉={X|X是投射kG-模}=〈k〉,M～k.

引理7设M,N,U,V是kG-模. 若M～N,U～V, 则下列结论成立:

1)M⊕U～N⊕V；

2)M⊗U～N⊗V.

证明： 1) 由引理3知,

〈M⊕U〉=〈M〉∩〈U〉=〈N〉∩〈V〉=〈N⊕V〉,

所以M⊕U～N⊕V.

2) 设X∈〈M⊗U〉, 则M⊗U⊗X是投射kG-模, 从而U⊗X∈〈M〉=〈N〉, 因此N⊗U⊗X是投射kG-模, 即U⊗N⊗X是投射kG-模. 类似地, 因为U～V, 所以V⊗N⊗X也是投射kG-模,X∈〈V⊗N〉, 可得〈M⊗U〉⊆〈V⊗N〉. 类似可得〈V⊗N〉⊆〈M⊗U〉, 表明M⊗U～N⊗V.

性质3设X,M,N是kG-模, 则下列结论成立:

1)X～X⊗X；

2) 进一步, 若M～N, 则X⊗M～X⊗N；

3)X⊗M～X⊗X⊗M.

证明： 1) 由引理4知1)成立.

2) 由引理7知2)成立.

3) 由1)和2)知3)成立.

性质4设M和N是kG-模. 若X是可裂迹kG-模, 则下列结论成立:

1)M～X⊗M；

2)M～N当且仅当X⊗M～X⊗N.

证明： 1) 由引理6和性质3知, 1)成立.

2) 由1)知2)成立.

定义4[11]设V是kG-模, 若k-内同态(k-自同态)模End(V)可以分解为平凡kG-模和投射kG-模的直和, 则称V是内平凡kG-模.

注5定义4中k-内同态模End(V)的G-模作用为：g·f=g-1fg,g∈G,f∈End(V). 内平凡kG-模在有限群的Dade群结构研究中应用广泛.

推论1设M和N是kG-模,X是内平凡kG-模, 则M～X⊗M, 并且M～N当且仅当X⊗M～X⊗N.

证明： 设X=V⊕S, 这里V是X的非投射直因子,S是X的投射直因子, 则V是可裂迹kG-模. 进一步, 结合性质4、 性质3和引理6知,M～V⊗M～X⊗M, 并且M～N当且仅当X⊗M～X⊗N.

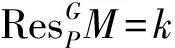
推论2设M和N是kG-模,X是平凡西罗限制kG-模, 则M～X⊗M, 并且M～N当且仅当X⊗M～X⊗N.

证明： 可证平凡西罗限制kG-模X是内平凡kG-模, 从而由推论1知结论成立.

性质5设M和N是kG-模, 则下列结论成立:

1)M～M*；

2)M～N当且仅当M*～N*.

证明： 1) 由性质1知1)成立.

2) 由1)知2)成立.

性质6设M和N是kG-模, 则下列结论成立:

1)Ω(M)～M；

2)M～N当且仅当Ω(M)～Ω(N).

证明： 1) 由性质1知1)成立.

2) 由1)知2)成立.

定理1(Green对应定理)[8]设G≥H≥NG(P), 这里P是群G的p-子群. 若U和V分别是不可分解kH-模和不可分解kG-模, 并且P是它们的顶, 则下列结论成立:

2) 对于g(f(V))≅V和f(g(U))≅U,f和g建立了顶为P的不可分解kG-模同构类及顶为P的不可分解kH-模同构类之间的一一对应(Green对应).

注6f和g保持顶为P的不可分解模的直和.f和g的直和扩充仍分别记为f和g.

定义6[12]设G>H, 若p||H|>, 但对每个t∈GH, 均有p⫮|H∩Ht|>, 则称H是G的强p-嵌入子群.

注7强p-嵌入子群在有限单群分类中应用广泛. 强p-嵌入子群H包含G的某个Sylowp-子群P的任意子群Q的正规化子NG(Q).

定理2设G≥H,M和N是kG-模, 则下列结论成立:

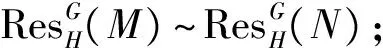
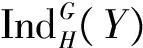
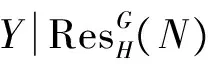
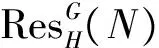
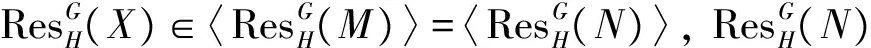
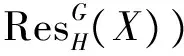
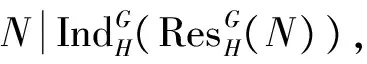
类似可证〈N〉⊆〈M〉, 所以M～N.

推论3设M和N是不可分解kG-模. 若H是G的强p-嵌入子群, 则M～N当且仅当其Green对应是Bousfield等价的.

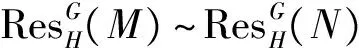
定理3设G≥H,M和N是kH-模, 则下列结论成立:

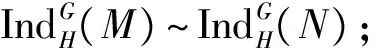
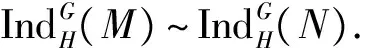
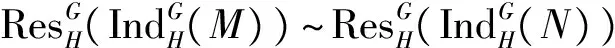
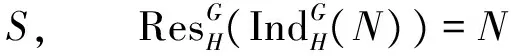
这里S和T是投射kH-模, 再结合引理6和引理7知,M～N.

推论4设M和N是不可分解kH-模. 若H是G的强p-嵌入子群, 则M～N当且仅当其Green对应是Bousfield等价的.

定理4设H是G的强p-嵌入子群, 则Green对应诱导出Stmod(kG)的全体Bousfield等价类(kG)与Stmod(kH)的全体Bousfield等价类(kH)之间的一一对应, 并且

(1)

(2)

F：(kG)→(kH), 《M》《f(M)》,M是不可分解kG-模；

G：(kH)→(kG), 《N》《g(N)》,N是不可分解kH-模.

首先, 由推论3和推论4知,F和G定义合理.

其次, 在H是G的强p-嵌入子群情形, 可设H包含任意不可分解kG-模(kH-模)的顶的正规化子. 由注6知, 此时Green对应保持任意不可分解kG-模(kH-模)的直和, 再由引理5和引理7知, 上述定义的映射F和G可以扩展到任意kG-模M和任意kH-模N上, 其扩展仍记为F和G.

再次, 由定理1知, 在不可分解kG-模(kH-模)上,GF=1,FG=1, 即F和G均为(kG)与(kH)之间的一一对应, 扩展后这两个等式也成立, 因此F和G的扩展也是(kG)与(kH)之间的一一对应.

最后, 对于任意不可分解kG-模M和不可分解kH-模N, 由推论3和推论4的证明知,

(3)

则在H是G的强p-嵌入子群情形, 由定理1和引理7知, 式(3)对于任意kG-模M和kH-模N也成立. 表明

(kH)=F((kG)

即式(1)成立. 类似可得式(2). 证毕.

[1] Bousfield A K. The Boolean Algebra of Spectra [J]. Comment Math Helvetici, 1979, 54: 368-377.

[2] Bousfield A K. Correction to the Boolean Algebra of Spectra [J]. Comment Math Helvetici, 1983, 58: 599-600.

[3] Bousfield A K. The Localization of Spectra with Respect to Homology [J]. Topology, 1979, 18(4): 257-281.

[4] Wolcott F L. Bousfield Lattices of Non-Noetherian Rings: Some Quotients and Products [J]. Homology, Homotopy & Applications, 2014, 16(2): 205-229.

[5] Iyengar S B, Krause H. The Bousfield Lattice of a Triangulated Category and Stratification [J]. Mathematische Zeitschrift, 2013, 273(3/4): 1215-1241.

[6] Iyengar S B. The Bousfield Lattice of the Stable Module Category of a Finite Group [R/OL]. 2017-05-22. https://www.math.unl.edu/～siyengar2/papers/Ow0211.pdf.

[7] Skowroński A, Yamagata K. Representations of Algebras and Related Topics [M]. Zürich: European Mathematical Society Publishing House, 2011: 55-83.

[8] Webb P. A Course in Finite Group Representation Theory [M]. Cambridge: Cambridge University Press, 2016.

[9] Happel D. Triangulated Categories in the Representation Theory of Finite Dimensional Algebras [M]. Cambridge: Cambridge University Press, 1988.

[10] Auslander M, Carlson J F. Almost-Split Sequences and Group Rings [J]. Journal of Algebra, 1986, 103(1): 122-140.

[11] Carlson J F, Thévenaz J. The Classification of Endo-Trivial Modules [J]. Invent Math, 2004, 158: 389-411.

[12] Salarian M R, Stroth G. Existence of Stronglyp-Embedded Subgroups [J]. Communications in Algebra, 2015, 43(3): 983-1024.