学科：小学数学连点成线串珠织网

王锦辉

接到送教下乡的任务，要到每个联盟学校上一节复习课，感觉任务艰巨，因为复习课不像新授课，有一个从“无”到“有”的过程，我想复习课至少要到达以下几个目的：一是回顾各知识点、进行查漏补缺；二是对知识点进行整理形成系统的知识体系，加深对知识的理解，提高综合运用知识的能力；三是培养学生自主整理、构建知识体系的能力。我认为的难点就在第三点，毕竟学生自主整理建构的能力是比较欠缺的。

按照上面的理解，我备了课，难点部分教学如下：

师：我们回忆了这些图形的面积计算公式的推导过程，你们有没有发现这些图形之间是有一定的联系的，请仔细想想，四人小组讨论讨论，摆摆它们的关系图。师：我们是把什么图形转化为什么图形或者是由那个图形的面积计算公式推导出那个图形的？生：长方形可以推导出平行四边形。生：平行四边形可以推导出三角形和梯形。生：圆可以剪拼成长方形。

……

做了一个练习题，课就匆匆收了场。

这个班因为数学老师有公事外出，由班主任语文老师带队上课。课罢，心直口快的语文老师马上就说：“你有些话说得不够通顺，学生很难理解，还有我觉得你话挺多的，感觉很啰嗦，另外，那个图形间的关系，这么难，他们怎么弄得出来。你让他们说，他们能说出什么？”我不住地思考用怎样的语言引导学生构建关系图？怎样才能让复习课更扎实有效，在回顾的基础上又有提升？

上课，听取意见，修改设計；再上课，听取意见，修改设计，终于在第五次的时候，有了自己期盼的教学效果，跟大家分享。

一、情境引入

师：同学们，今天我们要一起来上一节复习课。上复习课有什么用呢？用我们古人的一句话说：温故而知新。是的，大家请看这是我班学习书法的同学写的一个条幅（出示软笔书法作品条幅：温故而知新），请同学们看这个条幅，它是什么形状的，如果把它挂在我们教室的墙壁上，我们就需要装裱一下，装上边框安上玻璃，要用到哪些数学知识？生：装边框要算出长方形的周长，安上玻璃要算面积。师：是的。那么，今天我们就一起来复习平面图形的周长与面积。

二、明晰概念

师：我们都知道，这张条幅的形状是（长方形），除了长方形，整个小学阶段我们还学习过哪些基本的平面图形？（生叙述、师在黑板上张贴出示六个基本图形）

师：谁能举例说说什么是一个图形的周长和它的面积呢？谁上来举例子，说一说。

1.学生上前选择任意图形指出围成图形一周的长度是周长，而图形的面的大小是面积。

2.基于学生对周长与面积的理解，出示概念齐读一遍：封闭图形一周的长度叫做它的周长；物体表面或平面图形的大小叫做它的面积。

三、梳理公式

（一）回顾公式

1.请安静地回忆，填写相关公式。

2.汇报出示相关公式。课件中逐个出示相关公式。师：请大家看着字母公式一起用文字的形式读一遍。

3.回顾公式推导过程。

（1）关于周长公式。师：我们可以根据周长的定义，算出围成这个图形所有边长的总和求出没有周长计算公式的图形的周长。

（2）面积公式的推导：①长方形正方形的面积公式，课件演示长方形正方形面积公式的推导过程；②其它图形的面积公式。

（二）建构网络

师：刚才我们复习了平面图形的面积公式推导过程，同学们有没有发现在这些图形的面积推导过程中，它们是互相联系的，你能不能用一个简洁的图示表示出他们的关系，可以用箭头连接，四人小组讨论讨论，试着画画草图。

1.学生四人小组讨论，画图。

2.展示学生构建的关系图，说说这样连接的原因。

师小结：从左往右，根据长方形的面积公式可以推导出其他图形的面积公式；将一个未知图形转变成已知图形再进行研究的方法，是数学学习的重要方法，叫做：转化（板书），希望同学们今后能灵活运用转化的方法思考问题、解决问题。

（三）统一公式

1.学生独立思考后说说自己的想法。

2.师课件演示，梯形变为三角形、长方形、平行四边形，得出这些图形的面积计算公式可以统一为梯形的面积计算公式。

四、巩固练习

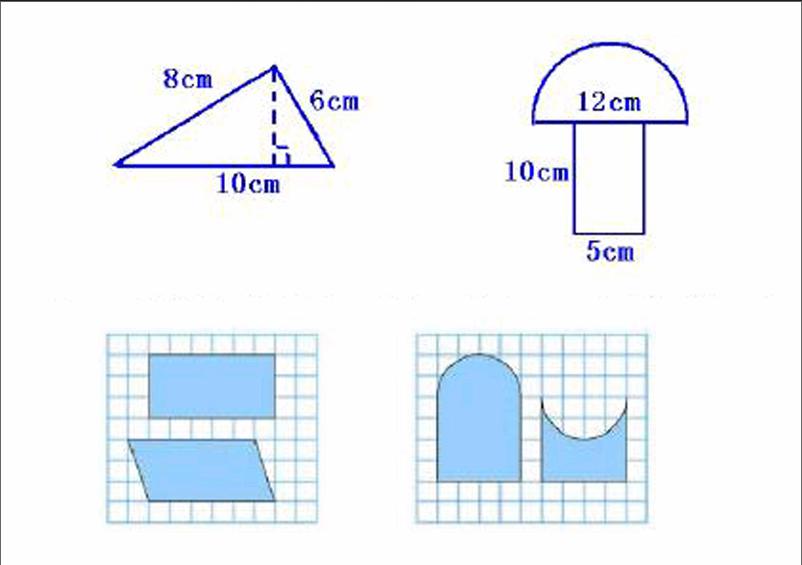
1.计算下面图形的周长与面积。

2.判断下面各题，正确的在（ ）里打“√”，错误的打“×”。

（1）三角形和梯形没有周长。（ ）

（2）半圆的周长等于圆周长的一半。（ ）

（3）两个面积相等的三角形能拼成一个平行四边形。（ ）

3.请大家仔细看这两组图形，认真审题，每组中的两个图形的周长和面积相等吗？

五、全课总结

上了这节课，你有什么收获？

课上完了，送教的任务完成了，说是送教，我想更是老师们共同学习的机会。老师们诚恳的建议，开诚布公的想法都让我心中涟漪无限。我自己经过历次磨课体会到：复习课并不是旧知的简单回顾，它有不同于新授课的目标，复习课一样要立足于学生，一样是一个动态生成的过程。endprint